文章信息
- 刘远刚, 郭庆胜, 孙雅庚, 杨乃, 郑春燕
- LIU Yuangang, GUO Qingsheng, SUN Yageng, YANG Nai, ZHENG Chunyan
- 地图自动综合中Beams移位算法的实现与改进
- Implementation and Improvement of Beams Displacement Algorithm in Automated Cartographic Generalization
- 武汉大学学报·信息科学版, 2016, 41(4): 450-454,540
- Geomatics and Information Science of Wuhan University, 2016, 41(4): 450-454,540
- http://dx.doi.org/10.13203/j.whugis20140343
-
文章历史
- 收稿日期: 2014-06-12

2. 长江大学地球科学学院, 湖北 武汉, 430100;
3. 武汉大学测绘遥感信息工程国家重点实验室, 湖北 武汉, 430079;
4. 中国地质大学(武汉)信息工程学院, 湖北 武汉, 430074;
5. 嘉应学院地理科学与旅游学院, 广东 梅州, 514015
2. School of GeoScience, Yangtze University, Wuhan 430100, China;
3. State Key Laboratory of Information Engineering in Surveying Mapping and Remote Sensing, Wuhan University, Wuhan 430079, China;
4. Faculty of Information Engineering, China University of Geosciences, Wuhan 430074, China;
5. School of Geograhical Science and Tourism, Jiaying University, Meizhou 514015, China
地图综合的过程中,由于比例尺缩小,难免会导致地图目标相互拥挤或符号重叠,产生空间冲突,从而破坏地图的清晰性和地图目标之间空间关系的正确性。然而,目前空间冲突的探测与处理尚未实现自动化,这成为阻碍地图自动综合发展的一个瓶颈问题。
移位是解决空间冲突的一种常用算子。众多学者围绕空间冲突问题提出了多种移位算法,大致可分为几何算法[1, 2, 3, 4, 5]和最优化算法两类[6, 7, 8, 9, 10, 11, 12, 13]。
Bader基于材料力学原理提出了一种能量最小模型——Beams模型[10]。该模型在继承Snakes模型优点的基础上,构建了一种面向地图二维平面的最优化模型。该研究中,将道路网看成是由多段细长的弹性杆件连接而成的整体结构,当道路中存在冲突时,就如同在这种结构上的冲突位置施加了外力。借鉴材料力学有关原理,弹性杆件在外力作用下表现出两个方面特征,或沿轴心方向的外力(正应力),使之产生拉伸或压缩变形;或垂直于轴心方向的力(剪应力),使之弯曲变形。这种可对伸缩或弯曲进行描述的模型,很好地刻划了地图上线目标的变形机理。起初,该模型仅用于线状目标的移位。为了将其应用于建筑物群的移位,Bader等还提出了一种辅助模型——Ductile Truss模型[11],以一组建筑物的中心点为结点构建最小生成树(minimum spanning tree,MST),得到了这些需要移位的建筑物的基本框架。该框架维持了建筑物群的空间关系和空间结构,从而将建筑物群的移位问题转换为其对应的Ductile Truss模型结点的移位问题,然后采用Beams模型求解。在国内,武芳等对Beams模型进行了深入研究,并将其与规则库相结合,成功地应用于数字地图中道路网的移位[12];侯璇等采用聚类方法,对空间点群(居民地)进行划分,然后对分区后的点群采用Beams算法进行移位[13]。
各种研究和应用表明,Beams模型用于解决地图上的点群、线(群)和离散面群的邻近冲突较为适用。然而,目前仍缺少对该算法实现细节的介绍,且无定量化的参数设置方法提出,因而限制了算法的应用。本文重点研究Beams移位算法在实现过程中的关键问题,并针对模型材料参数设置问题,提出一种自适应参数设置方法,从而对算法进行改进。
1 Beams算法实现与改进 1.1 基本数学模型能量最小移位算法的求解一般采用有限元方法[9, 10, 11, 12],建立形式为Kd=f矩阵方程,解之,得到移位向量d。其中,K为刚度矩阵,f为外力向量,它们可分别通过聚合所有单元的的刚度矩阵和外力向量得到。
Beams模型中,有限元单元的矩阵方程为(具体推导过程可参考文献[10]):

式中,Ke为单元刚度矩阵;fe为单元外力向量;de为单元移位向量,完整矩阵形式为:

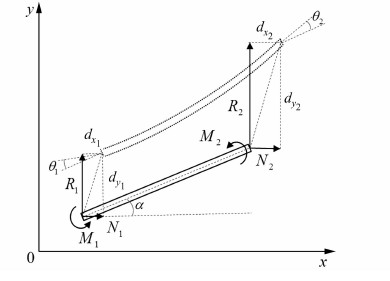
式中,l为单元的长度;s和c分别为单元方位角的正弦sinα和余弦coso;如图 1所示,(N1,R1,M1)和(N2,R2,M2)分别为单元首末点处沿x轴和y轴方向的外力,以及合力矩;(dx1,dy1,θ1)和(dx2,dy2,θ2)分别为单元首末点处x轴和y轴方向的移位以及旋转角度,它们是方程中的未知数;E为单元的弹性模量,I为惯性矩,A为横截面积,三者均为待定参数。其中单元端点处所受外力通过冲突探测得到,而单元端点处的力矩,物理学上指的是使物体转动的力乘以到转轴的距离,即M=F×L(L是从转动轴到着力点的矢量,F是力矢量)。计算时,可分别求出单元端点处的x轴和y轴方向外力的力矩,再求和得到总力矩,计算公式为:
|
| 图 1 Elastic Beam单元受力分析 Fig. 1 Force Analysis of an Elastic Beam Element |
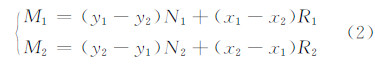
式中,(x1,y1)和(x2,y2)分别为单元线段首末端点的坐标。
1.2 刚度矩阵和外力向量的计算与聚合一般地,对于一个包含n(n>1)个节点的Beams模型,将其包含的每一条边作为一个有限元单元,总体刚度矩阵K可由各个单元的刚度矩阵Ke组装而成,且它是一个大小为3n×3n的带状对称矩阵。与之类似,总体外力向量f也由单元外力向量fe组装得到,它是一个元素个数为3n的向量。为了维护单元与单元之间的关联关系,需要先将所有节点进行统一编号,再按编号进行单元矩阵的聚合,从而得到总体刚度矩阵。首先,初始化总体刚度矩阵和总体外力向量(按顶点的个数创建矩阵和向量,并将元素初值设为0);然后,根据式(1)、(2)及冲突检测的结果,计算出每个单元的刚度矩阵和外力向量;最后,按照单元线段两顶点的编号“对号入座”,将它们分别累加到总体刚度矩阵和总体外力向量对应的位置。图 2给出了单元两端点编号分别i、j时,每一个单元刚度矩阵元素在全局刚度矩阵中的对应下标。
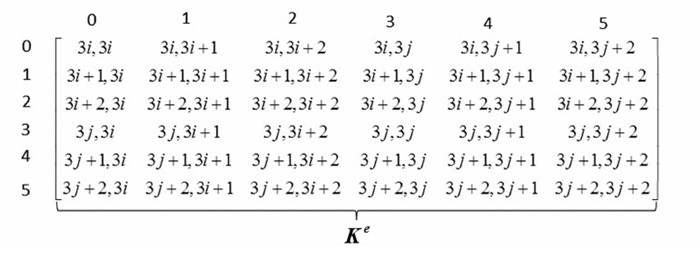
|
| 图 2 单元矩阵各元素在全局矩阵中对应下标 Fig. 2 Global Index of Each Item in the Element Stiff Matrix |
采用该算法移位的结果受模型材料参数影响,如弹性模量E,惯性力矩I和横截面积A等。为了降低各种影响因素的复杂性,同时设置比较合适的参数,将I和A设定为常量,通过动态调节E的值使移位的大小控制在合理的范围内。本文在以上条件的限定下,提出了一种自适应设置参数的方法,该方法通过两次计算移位量估算出较合适的E值。第一次计算过程中将E设为一个大于0的任意值E0,代入模型计算出各点的移位向量。假设最大受力处的移位量恰好也是最大的,则合适的E值可通过以下经验公式得到:
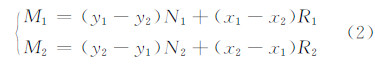
式中,fmax为最大的外力值;d0max为第一次计算出的对应的移位量。将估算出的E再次代入模型进行第二次计算,新计算出的最大受力处的移位值dmax可基本与fmax相等(dmax≈fmax)。这样可保证最严重的冲突得到解决。实验经验表明,在移位操作区的划分比较合理,使移位能够充分传播的情况下,以上假设成立。关于移位操作区的划分,可参考文献[11]中的方法。另外,将参数设置为IA时,对线状要素的移位效果较好,而将参数设置为I≈A时,对点群或离散面群的移位的效果较好。
2 实 验地图目的移位问题可分为两类[7, 9]:(1)针对不可变形目标(如点目标或小面积面目标)的平移;(2)针对可变形目标(如线目标或大面积面目标的边界线)的变形。对应地,建筑物与道路是两类最具代表性的地图要素,为了演示Beams模型应用于地图要素移位的有效性和适用性,本文分别对道路和建筑物群进行移位实验。实验中,分别将道路要素中心线上的线段和建筑物群的邻近图的边作为Beams模型基本单元,以约束Delaunay三角网(constrained delaunag triangulation,CDT)作为辅助数据结构[14],实现了地图目标之间邻近冲突的探测与建筑物群邻近图的建立,相关细节可参考文献[15]。
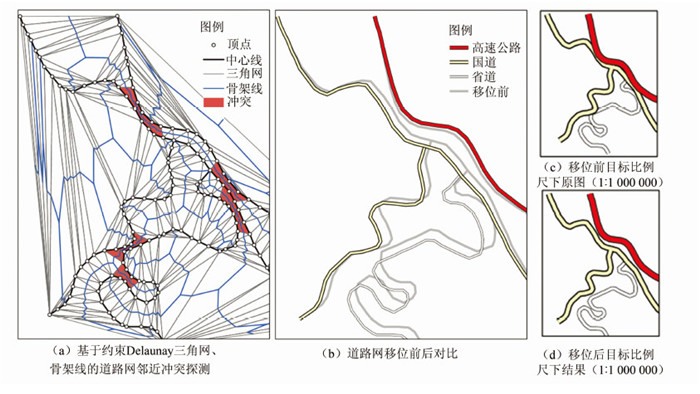
2.1 道路移位实验图 3表述了道路移位的基本过程。首先,针对道路中心线建立约束Delaunay三角网,并从中提取骨架线;然后沿各条骨架线判定其左右路段或同一路段中一个弯曲的左右分支之间的间隔区域是否达到距离阈值,从而探测出冲突的范围和大小,再根据冲突探测的结果计算出外力向量;最后,调用Beams模型进行移位。本文实验中,目标比例尺为1∶1 000 000,高速公路、国道和省道符号宽度分别为1.4 mm,1.0 mm和0.8 mm,图上最小间隔距离阈值为0.2 mm,参数I和A分别设为107和1。移位后的道路网中各处冲突已基本解决,同时,较好地保持了道路的形状特征和道路网的拓扑关系。
|
| 图 3 道路网移位 Fig. 3 Road Displacement |
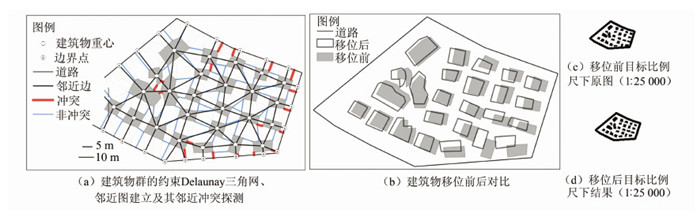
图 4表述了建筑物移位的基本过程。实验中,用建筑物的重心代替建筑物,借助CDT建立反映建筑物群空间分布的邻近图,然后采用Beams算法进行建筑物移位。其中,邻近图中的结点除了所有建筑物重心外,还包括街边建筑物重心在其毗邻街道上的最近点。这些点在移位过程中作为Beams模型的边界条件固定不动。冲突的探测也通过CDT实现,不同的是进行邻近分析时,需先将建筑物多边形内部和凹部三角形剔除;再计算每一对邻近建筑物之间以及街边建筑物与其毗邻的街道之间的最近距离,检测出所有邻近冲突;然后,根据这些冲突计算出每个建筑物的受力;最后,调用Beams模型进行移位。本例中,目标比例尺为1∶25 000,街道线宽为0.6 mm,图上最小间隔距离阈值为0.2 mm,参数I和A均设为1。移位后的结果已基本解决各处冲突,且较好地保持了建筑物群的整体分布和空间关系。
|
| 图 4 建筑物移位 Fig. 4 Building Cluster Displacement |
本文对基于Beams模型的移位算法进行深入研究,介绍了该算法的数学模型与有限元求解方法,从算法实现的角度着重分析了模型刚度矩阵和外力向量的计算和聚合等关键问题。针对模型材料参数设置问题,提出一种自适应参数设置方法对算法进行改进。为了验证改进算法的可行性和适用性,分别对道路网和建筑物群实验数据进行移位,演示了对线状和离散面状地图目标进行冲突探测、冲突表达和移位的基本思路。结果表明,改进后的算法具有较强的适用性,不仅能用于线目标的位移,而且能用于点群和面(群)目标的位移。可以推测,该算法也可用于具有较大面积的面状目标边界线的局部变形处理。下一步将继续深入研究Beams模型参数与地图目标特征及地图综合约束条件之间的依赖关系,寻求更完善的参数设置模型。另外,算法需要解算较大的稀疏矩阵方程,占用计算资源大。为此,可采用更优的稀疏矩阵求解方法,以降低计算资源的开销。
| [1] | Lichtner W.Computer-assisted Processes of Cartographic Generalization in Topographic Maps[J]. Geo-Processing, 1979, 1(1):183-199 |
| [2] | Nickerson B G. Automated Cartographic Generalization for Linear Features[J].Cartographica, 1988,25(3):15-66 |
| [3] | Ruas A. A Method for Building Displacement in Automated Map Generalisation[J]. International Journal of Geographic Information Science, 1998,12(7):789-803 |
| [4] | Ai Tinghua. A Displacement of Building Cluster Based on Field Analysis[J]. Acta Geodaetica et Cartographica Sinica, 2004,33(1):89-94(艾廷华.基于场论分析的建筑群的移位[J]. 测绘学报,2004,33(1):89-94) |
| [5] | Fei Lifan, He Jin. Displacement Models for Solving Graphic Conflicts Between Streets and Buildings[J]. Geomatics and Information Science of Wuhan University, 2007, 32(6):540-543(费立凡, 何津. 解决街道与建筑物图形冲突的移位模型研究[J]. 武汉大学学报·信息科学版, 2007, 32(6):540-543) |
| [6] | Burghardt D, Meier S. Cartographic Displacement Using the Snakes Concept[OL]. https://www.researchgate.net/publication/268018456_Cartographic_displacement_using_the_snakes_concept,2005 |
| [7] | Harrie L. An Optimisation Approach to Cartographic Generalisation[D]. Sweden:Lund University, 2001 |
| [8] | Hojholt P. Solving Local and Global Space Conflicts in Map Generalization:Using a Finite Element Method[J].Cartography and Geographic Information Science, 2000, 27(1):65-73 |
| [9] | Mao Jianhua, Guo Qingsheng. Maintenance of Spatial Relation in Map Objects Displacement[J]. Geomatics and Information Science of Wuhan University, 2003, 28(6):492-495(毛建华, 郭庆胜. 地图目标移位的空间关系维护[J]. 武汉大学学报·信息科学版, 2003, 28(4):492-495) |
| [10] | Bader M. Energy Minimization Methods for Feature Displacement in Map Generalization[D]. Zürich:University of Zürich, 2001 |
| [11] | Bader M, Barrault M, Weibel R. Building Displacement over a Ductile Truss[J]. International Journal of Geographical Information Science,2005,19(8,9):915-936 |
| [12] | Wu Fang, Hou Xuan, Qian Haizhong, et al. A Model for Road Network Displacement in Automated Map Generalization[J]. Acta Geodaetica et Cartographica Sinica, 2005,34(3):262-268(武芳,侯璇,钱海忠,等. 自动制图综合中的线目标位移模型[J].测绘学报,2005,34(3):262-268) |
| [13] | Hou Xuan, Wu Fang, Liu Fang, et al. A Model for Point Cluster Displacement in Automated Generaligotion[J]. Science of Surveying and Mapping, 2005,30(2):44-47(侯璇, 武芳, 刘芳,等.基于弹性力学思想的居民地点群目标位移模型[J]. 测绘科学,2005,30(2):44-47) |
| [14] | Zheng Chunyan, Guo Qingsheng, Hu Huake, et al. Method for Constructing the Hierarchical Structure of Contour Lines Based on Constrained Delaunay Triangulation[J]. Geomatics and Information Science of Wuhan University, 2008, 33(5):524-527(郑春燕, 郭庆胜, 胡华科, 等. 基于约束Delaunay三角网建立等高线层次结构的方法[J]. 武汉大学学报·信息科学版, 2008, 33(5):524-527) |
| [15] | Liu Yuangang, Guo Qingsheng, Sun Yageng. A Complete Solution of Cartographic Displacement based on Elastic Beams Model and Delaunay Triangulation[C]. The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Suzhou, China, 2014 |
 2016, Vol. 41
2016, Vol. 41



