文章信息
- 翟卫欣, 程承旗, 童晓冲, 陈波
- ZHAI Weixin, CHENG Chengqi, TONG Xiaochong, CHEN Bo
- 利用地球立体剖分格网生成Subdivision R-树索引模型
- Subdivision R-Tree Index Model of the Earth-based Three-dimensional Subdivision Grids
- 武汉大学学报·信息科学版, 2016, 41(4): 443-449
- Geomatics and Information Science of Wuhan University, 2016, 41(4): 443-449
- http://dx.doi.org/10.13203/j.whugis20140104
-
文章历史
- 收稿日期: 2014-11-28

2. 北京大学工学院, 北京, 100871;
3. 北京师范大学地表过程与资源生态国家重点实验室, 北京, 100875;
4. 空军空降兵学院, 广西 桂林, 541003
2. College of Engineering, Peking University, Beijing 100871, China;
3. State Key Laboratory of Earth Surface Process and Resource Ecology, Beijing Normal University, Beijing 100875, China;
4. Air Force Airborne Academy, Guilin 541003, China
随着空间对地观测技术的发展,三维地理空间信息获取与更新的能力有了飞速的进步,海洋、环境等地学应用领域已逐步形成多维空间信息源[1]。同时,随着多种数据获取手段的不断成熟和发展,大数据研究引起了产业界、科技界和政府部门的高度关注[2]。如何能够在原有的基础上建立满足要求的空间索引来完成空间数据的高效组织已经成为了重要的研究内容。
空间索引在空间数据库中占据重要地位,一直以来都是数据库研究的重点。1974年Finkel和Bentley合作提出了四叉树概念[3],体现了多级索引的思想。而以四叉树为代表的网格索引(空间上拓展为八叉树)是一种基于刚性的空间划分的空间索引,会出现一些问题,例如,大量目标及其最小外包矩形的映射跨越多个格网,导致索引重复,存储量大大增加;即使一些目标能够映射到单一格网中,也存在格网尺度与目标尺度差距过大的问题,导致索引的冗余较大;这些问题将直接导致区域查询效率较差。
1984年,Guttman提出了R-树[4]的数据结构,是R-树类索引族的基础;1987年,Sellis等设计了R+树[5];1990年,Beckmann等设计了R*树[6]; 1994年,Kamel等提出了Hilbert R-树[7]。R-树及其各种变体一经提出,即成为常用的空间数据组织形式。R-树的主要问题是中间目录矩形的大量重叠会导致查询路径的不唯一,严重影响性能。在现有的常见的空间数据的索引中,单一索引往往存在各种各样的问题,而混合索引的出现则能够帮助克服各单一索引的缺陷,解决各自存在的问题[8]。郭菁等[9]和FU等[10]先后提出了QR-树的概念,即将整个索引空间划分成多级子索引空间,然后对每级的子索引空间均采用R-树进行索引;其实质是将一棵较大的R-树分解成多棵较小的R-树,从而减少索引空间重叠,提高查询性能。邱建华等在R*树索引模型的基础上融合了传统的四叉树索引方法的精髓,提出了一种改进的QR*树索引[11]。黄明等在QR-树的基础上提出了一种改进QR-树的数据模型来建立高效的空间数据索引,通过检测水平和垂直相交区域以确定图元所属节点,从而实现海量数据的快速检索[12]。赵楠提出的基于网格与R-树的混合索引方案首先将矩形地理空间进行粗网格划分建立多级网格索引,然后针对每个小网格建立基于R树的空间索引[13]。QR-树的思想近年来在城镇化系统数据整合、海上移动自组网、地下空间索引等领域都有着广泛应用[14, 15, 16]。
以上所述的QR-树和各类QR-树索引结构在每个网格中均使用单一的R-树索引来进行数据管理,这些索引虽然能够有效地改进八叉树索引的效率,但是没有考虑到空间实体本身的模型特点,存在一定的问题。网格内部的R-树的插入、删除过程较为复杂,R-树的结构越复杂,层级越深,查询的效率可能会更高,但更新维护的工作量较大,极端情况下整个索引都可能重建。当需要做较多的更新操作时,索引结构需要实时调整,效率大幅降低。因此,简单地将格网与R-树结合构建的索引缺乏选择性,没有完全结合网格索引和R-树的特点,维护代价太大。
本文针对三维数据管理中八叉树索引冗余大、R-树索引插入删除过程复杂的问题,依托GeoSOT地球立体剖分格网,提出了一种新的八叉树与R-树有机结合的Subdivision R-树索引模型。Subdivision R-树是建立在GeoSOT全球剖分网格的基础上的索引方式。建立这种新的地球系统空间索引方式能够充分利用地球系统格网的多层结构特征和编码代数运算的优势,依据原有的数据库索引模式的基础对空间目标进行有效管理,避免索引重复、冗余,提高查询效率。
1 Subdivision R-树索引模型的构建基础Subdivision R-树索引模型的构建基础是最小空间范围体和GeoSOT网格。本文所指的最小空间范围体是Subdivision R-树索引模型所管理的空间对象的形式,类似于二维的最小外包矩形;GeoSOT网格则是指本文所采用的的全球剖分网格。
1.1 最小空间范围体在二维空间中的最小外包矩形(minimum bounding rectangle,MBR)是包围图元,且边均平行于坐标轴的最小的矩形。设图元的X、Y方向的最大最小值分别为xmax、xmin、ymax、ymin,则MBR的四个角点坐标分别是(xmax,ymax)、(xmax,ymin)、(xmin,ymax)、(xmin,ymin)。据此本文对其加以拓展设计了以地球为目标的、适用于三维空间的GeoSOT网格需求的最小空间范围体的结构。用6个变量来定义一个空间最小外包范围体,分别为半径r1(r1>0)、半径r2(r2>0)、经度α1(-180°<α1<180°)、经度α2(-180°<α2<180°)、纬度β1(-90°<β1<90°)、纬度β2(-90°<β2<90°)。在地球空间中(不仅包括地球表面,还包括地球内部和外层空间),包含地球球心和经度为α1、α2的两条经线形成的两个平面,连接地球球心和纬度为β1、β2的纬线构成的两个曲面以及以地球球心为球心r1和r2为半径构成的两个球面。这六个面所包围形成的封闭空间块即为一个空间最小外包范围体。
一个空间最小外包范围体共包含有6个面,如图 1所示。图 1中,上表面Su(曲面ABCD)(或者下表面Sd(曲面A′B′C′D′)),是以地心为球心的球面; 东表面Se(平面AA′D′D)(或者西表面Sw(平面BB′C′C)),是经过地轴的平面,该平面与地球表面的交线是一条经线; 南表面Ss(曲面ABB′A′)(或者北表面Sn(曲面CC′D′D)),是经过地心的光滑曲面,该曲面与地球表面的交线是一条纬线。
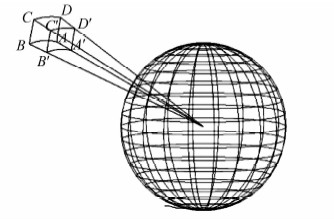
|
| 图 1 GeoSOT网格的最小空间范围体结构 Fig. 1 Structure of 3D-MBR of GeoSOT |
空间信息剖分组织的基本思路是基于地球空间剖分理论,为全球空间信息建立多级索引,根据地球空间剖分框架中离散剖分面片的结构体系,设计地球空间剖分数据模型,设计大到整个地球、小到cm级精度的全球空间信息索引体系,实现海量空间数据的快速检索和更新[17, 18, 19]。
GeoSOT网格是一套以空间信息剖分组织理论为基础的全球空间信息组织方式。GeoSOT索引基于经纬度坐标空间定义,原点为本初子午线与赤道的交点。GeoSOT采用全四分递归剖分。为使网格大小保持整度、整分和整秒,GeoSOT将地球经纬度坐标空间做了三次扩展,将360°×180°空间扩展到512°×512°,将每度的60′空间扩展到64′,将每分的60″空间扩展到64″。GeoSOT的0级网格为经纬度坐标512°×512°空间,对应信息体区域为全球。接下来,下一级剖分面片由上一级剖分面片递归四叉划分得到,直到32级为止。32级网格大小为1/2 048″×1/2 048″[20]。
1.2.2 三维GeoSOT网格GeoSOT-3D立体剖分格网模型将二维剖分面片的概念扩展至三维立体空间,对GeoSOT平面面片沿法线方向延展,即可形成“面片柱”。将面片柱按高度维剖分框架分为多个“柱段”,构成剖分“体块”,即三维剖分框架中的离散分割单元。基于上述设计,设高度维取值范围为[hs,hs+2n\5d](单位为m),其中hs为地理空间实体的下界,取其为地球表面到地心的距离的负值,即hs=-R,R为设定的地球半径,n是层级数;取值范围是[0,32](与GeoSOT二维编码的32级相对应);d为高度维进行第n层级剖分后的层间隔。
八叉树体块(以下简称体块)是立体剖分格网的基本单元。将整个GeoSOT-3D剖分空间视作以经纬网为xy平面、以高程为z轴的立方体,对立方体按照GeoSOT剖分规则进行逐层八叉树划分所形成的体块。八叉树体元的形态如图 2所示。对于第m级的二维剖分面片S,在该二维面片所对应的高维度空间内将会存在232-m个分层,即高度维剖分层级始终与二维剖分层级相等。

|
| 图 2 三维GeoSOT网格剖分体元 Fig. 2 Volumn Element of 3D-GeoSOT Grid |
Subdivision R-树的核心思路是通过八叉树和R-树混合索引结构来共同管理空间中的三维数据,在八叉树网格索引的基础上,有选择地建立R-树。在网格内部,将不同的空间数据所对应的最小空间范围体分别对待,尽量使得网格内部达到平衡。
2.1 两类最小空间范围体的划分我们将处于不同空间目标的最小空间范围体根据其尺度和位置特点分成两类。
第一类:空间目标的最小空间范围体完全属于某一层次的GeoSOT-3D立体格网,并且最小空间范围体的尺度和该层次格网的粒度差距不大(两者的尺度比大于某一阈值);
第二类:空间目标的最小空间范围体不完全属于某一层次的GeoSOT-3D立体格网,或者即使属于某一层格网,也会导致尺度差异过大(两者的尺度比小于某一阈值),带来索引的冗余。
对于这两类目标,第一类可以直接使用GeoSOT-3D构成的空间八叉树作为索引进行管理;第二类,如仍采取空间八叉树的方法则效率不高。并且考虑到空间目标的动态特性,第一类和第二类的快速切换也十分常见。
针对第二类目标,我们考虑将二维情况的R-树索引引入三维空间,让它配合GeoSOT-3D格网空间的八叉树索引共同使用,称其为Subdivision R-tree Index,简称Subdivision R-树索引。基于此,可以利用八叉树索引管理第一类目标,用R-树管理第二类目标。
2.2 Subdivision R-树索引模型的构造Subdivision R-树是以八叉树索引为主枝,将R-树嫁接到上面,形成一棵混合的树型模型。这种方式的核心是将一棵大的R-树分解成若干小的R-树,将每一棵小的R-树嫁接到八叉树的对应枝上,这样,合成的Subdivision R-树一方面保持了八叉树固定空间索引的优势,另一方面,将那些无法用固定格网管理的空间对象(跨格网的对象)用R-树管理起来。另外,新形成的Subdivision R-树在每个八叉树节点上生成一棵小的R-树,将大的整体复杂的R-树分散在小范围内管理。理论上,对于R-树的任意一枝都可以嫁接到八叉树上,最极端的情况下,某一枝也可以直接隶属于八叉树的根节点。混合索引结合了两种索引各自的优势,建立了内部R-树的八叉树,其数据量由于部分分离而冗余减少;而大的R-树被分解成多棵小的R-树后树的层次减少,也避免了R-树的树形结构整体调整,因而其插入、删除过程也得到了改进。
2.3 Subdivision R-树索引的基本算法设计 2.3.1 检索算法1) 给定检索范围(包括经度范围、纬度范围、高度范围)。
2) 从Subdivision R-树的根结点开始,假设该结点与检索范围相交,则进行网格检索;如果根结点关联的子空间即对应R-树的索引空间相交,则须在该R-树中进行检索操作。
3) 对于每一子结点,比较其关联子空间是否与检索范围相交,若否,则该结点及其子树截断,再继续往下查询;如是,进行网格检索和R-树的检索。按照循环步骤1)~3)比较下一级的子结点,直到全部检查完成。
2.3.2 插入算法1) 获得Subdivision R-树根节点作为当前结点和待插入的空间体的最小空间范围体MBR。
2) 计算出待插入的MBR是否能被完全包含在当前结点的子结点中;是则对能够完全包含的子节点继续步骤2)操作,否则转到步骤3)。
3) 判断当前待插入的MBR的空间尺度相对当前结点的尺度的比值是否大于阈值,如果是,则直接在网格中插入;否则在网格对应的R-树中进行插入操作。
2.3.3 删除算法1) 获得Subdivision R-树根节点作为当前结点和待删除的空间体的最小空间范围体。
2) 如果当前结点是叶节点,则转到步骤4)。
3) 如果是非叶节点,则在其子节点的空间中查询完全包含该最小空间范围体的结点,若能找到,则设能完全包含的子节点为当前结点并转到步骤2);否则,转到步骤4)。
4) 判断当前待删除的最小空间范围体的空间尺度相对当前结点的尺度的比值是否大于阈值,如果是,则直接在网格中删除;否则,在网格对应的R-树中进行删除操作。
3 实验设计 3.1 实验一:性能对比为了评估Subdivision R-树的性能,本文编写了八叉树、QR-树、Subdivision R-树的实验程序,并对不同数据类型的三种空间索引分别进行了比较,从比较结果中得出Subdivision R-树索引与传统立体剖分索引的差别。
我们选用整个索引空间(即模拟的地球空间)随机分布的三维矩形,模拟最小空间范围体来完成对于三种空间索引进行的查询和更新的耗时对比。
我们所采用的第一类数据整体地分布在整个三维空间中,坐标x、y、z随机生成,主要用来模拟整个地球空间中的无序的各类空间数据分布;第二类数据整体地分布在三维空间中某几个不重合的子空间中,在各个子空间中数据是无序分布的,主要用于模拟某些在个别位置较为集中而其他地方数据较少的分布方式;第三类分布与第二类分布相比,分布区域更为集中,用于模拟某些在个别区域有非常集中的数据而其他地方数据分布较少的分布方式。
对三类不同的数据分布分别取10个不同的样本来做模拟实验,测量3类索引模型在3种不同的数据分布下进行等次各类数据索引操作的耗时均值来评测各自的性能。3种空间索引操作的耗时对比如表 1所示。
| 索引结构 | 第一类数据分布 | 第二类数据分布 | 第三类数据分布 | ||||||
| 插入 | 删除 | 检索 | 插入 | 删除 | 检索 | 插入 | 删除 | 检索 | |
| 八叉树 | 2 558 | 198 011 | 5 098 | 1 260 | 302 812 | 5 145 | 1 578 | 285 335 | 5 132 |
| QR-树 | 5 422 | 19 490 | 5 272 | 14 891 | 26 205 | 5 375 | 16 735 | 29 742 | 5 335 |
| Subdivision R-树 | 4 721 | 18 239 | 5 126 | 11 829 | 23 910 | 5 199 | 13 298 | 23 903 | 5 261 |
总体来讲,3类索引模型在检索方面的差距很小,而八叉树的检索效率整体上稍有优势。但是在数据更新方面(包括数据插入和数据删除),QR-树和Subdivision R-树两类混合索引的优势明显。这是因为,普通的八叉树索引在对每一个对应的格网内部并没有建立对应的优化策略;而其余两种则利用R-树(或者部分R-树)来进行管理。尽管插入时R-树比八叉树慢,但在进行正常的数据更新时,无须线性地将每个网格内部的数据依次遍历,因此成倍或几倍地提高了更新的效率。而对于第二类和第三类空间数据,许多分布得比较紧密的数据无法在整个网格中散开,只能集中于某几个节点,这就造成网格索引的化整为散的特点体现不充分。
图 3给出了对于两种内含R树索引的效率对比。在第一类分布条件下,两种模型的效率差距并不大。而对于第二类和第三类分布的,插入和删除的差距较为明显,且第三类分布的差距更为明显。第二类数据的插入效率提升约20%,删除效率提升约10%,第三类数据的插入和删除效率提升均达到20%。实验结果说明,在极个别点集中分布的较大数据的节点内部建立R-树能够实现有效管理,其中Subdivision R-树相较QR-树的性能更优。因为在空间目标差异过大、数据量较多时,空间目标的聚集性不佳,R-树的重叠性可能会很大,此时的R-树模型复杂且层级较深,效率较低。而Subdivision R-树不是将数据唯一地存在R-树中,而是有选择地将部分不便于网格管理的数据分给内部的R-树来管理。Subdivision R-树对于空间范围内的第二类数据进行了局部聚类,使得数据量变小,聚类的复杂度也大幅降低,并且各个小空间内的聚类独立,可以进行并行计算,使效率进一步提高。
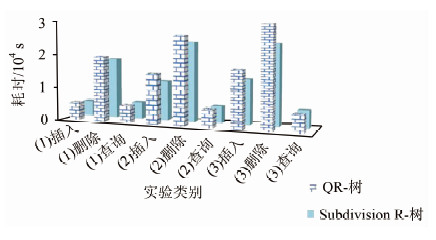
|
| 图 3 QR-树与Subdivision R-树效率对比 Fig. 3 Comparison of QR-tree and Subdivision R-tree |
Subdivision R-树对应的阈值是该树的一项重要属性,它的取值常常会影响到整个Subdivision R-树的效率。阈值是判别最小空间范围体是直接被网格管理还是被R-树管理的标准。一棵好的Subdivision R-树需要有一个合适的阈值来对空间数据进行分类,进而平衡整个网格和相应的R-树的数据量分布。
Subdivision R-树相对于QR-树在网格内部的提高主要体现在通过阈值的选取将数据分散到网格和R-树中管理。网格索引和R-树索引耗时均随着数据量的增加而提高。网格索引的耗时提高基本上是一条平滑的曲线,而R-树索引的耗时提高比网格索引略慢。但在数据量增加到一定量之后,耗时会突然增加(因为会出现树形结构的整体调整)。图 4描述了这种关系。在Subdivision R-树中,随着R-树管理的数据量的增加,R-树的耗时增加,在A-B和C-D段尤其显著;同时网格的耗时在减小,总耗时也在图 4中标明,P点即为一个总体耗时的极小点,在P点处两者的结合数据分配是最优的。

|
| 图 4 耗时与数据分配的关系 Fig. 4 Relation of Time Consuming and Data Distribution |
通过阈值的选取可对数据进行分类,分别分配给网格和R-树来管理,实现图 4所示的效率提高。实验二中对于上文所提到的三类数据分布分别用Subdivision R-树来进行插入、删除、检索的操作,其依次为0.1、0.2、0.3、0.4、0.5、0.6,用于评测最优的阈值选取。实验结果如表 2所示。
| 阈值 | 第一类数据分布 | 第二类数据分布 | 第三类数据分布 | ||||||
| 插入 | 删除 | 检索 | 插入 | 删除 | 检索 | 插入 | 删除 | 检索 | |
| 0.1 | 4 792 | 22 481 | 5 111 | 14 004 | 31 721 | 5 102 | 11 309 | 23 175 | 5 132 |
| 0.2 | 4 722 | 22 196 | 5 187 | 13 928 | 29 206 | 5 232 | 10 423 | 21 490 | 5 107 |
| 0.3 | 4 801 | 21 904 | 5 221 | 12 681 | 22 129 | 5 291 | 10 523 | 21 006 | 5 144 |
| 0.4 | 4 734 | 18 861 | 5 141 | 10 023 | 20 920 | 5 206 | 12 921 | 23 782 | 5 222 |
| 0.5 | 4 721 | 18 239 | 5 126 | 11 829 | 23 910 | 5 199 | 13 298 | 23 903 | 5 261 |
| 0.6 | 4 792 | 20 079 | 5 092 | 13 421 | 25 928 | 5 182 | 13 806 | 23 903 | 5 193 |
通过对实验二中实验结果的分析可以看出,在数据的检索方面,阈值的影响同样不是十分明显。但是在更新方面,Subdivision R-树中的阈值选取不宜过大,否则针对较大数量的最小空间范围体都需要在各个节点内建立R-树索引,会导致更新效率的降低;假设所选取的阈值过小,查询的冗余又会增加,从而导致效率下降,而在三维环境中,一个方向的尺度变化会导致整个立体尺度的立方变化,因此阈值的细微变化可能会对整个Subdivision R-树的效率产生一定影响。阈值在0.3~0.5之间的Subdivision R-树往往效率较高,而当数据相对集中分布的时候,R-树索引中的数据量将会较大,而网格中的数据量较少;此时需要将阈值稍微降低,将部分数据从R-树中分离出去来进行平衡,这样才可以保持较高的更新效率。
4 结 语本文提出了一种新型的数据组织形式Subdivision R-树,实现了对于数据更新、查询的高效管理。通过多方面的实验测试与对比,验证了Subdivision R-树剖分网格的更新检索能力在多方面都比普通的立体剖分网格形式有提高。Subdivision R-树索引模型对于全球尺度的空间数据能够进行高效管理,尤其对于需要及时的移动目标数据适应性较强。
Subdivision R-树是以GeoSOT网格为基础的索引,它以整个地球空间为目标对象,能够对三维立体空间的空间数据进行分层索引; 相比R-树索引,能够将R-树分支在不同的网格中,相比网格索引,能实现对每个网格内部的优化管理,通过R-树索引和八叉树索引两种索引来共同管理空间数据,提升了数据更新的效率; 在网格内部,能够根据最小空间范围体和当前网格的尺度之比有区别地对待不同尺度的空间数据,将不同尺度的空间数据选择性地分配给R-树索引或八叉树索引来管理,效率有所提高,在数据分布较为集中的情况下,效率可提高20%。
| [1] | Chen Shupeng. Geo-spatial/temporal Analysis[J].Journal of Remote Sensing, 1997,1(3):161(陈述彭. 遥感地学分析的时空维[J]. 遥感学报,1997,1(3):161) |
| [2] | Li Guojie, Cheng Xueqi. Research Status and Scientific Thinking of Big Data[J]. Bulletin of Chinese Academy of Sciences, 2012,27(6):647-657(李国杰,程学旗. 大数据研究:未来科技及经济社会发展的重大战略领域——大数据的研究现状与科学思考[J]. 中国科学院院刊,2012,27(6):647-657) |
| [3] | Finkel R A, Bentley J L. Quad Trees a Data Structure for Retrieval on Composite Keys[J]. Acta Informatica,1974,4(1):1-9 |
| [4] | Guttman A.R-trees:A Dynamic Index Structure for Spatial Searching[J]. ACM, 1984,14(2):47-57 |
| [5] | Sellis T, Roussopoulos N, Faloutsos C. The R+-tree:A Dynamic Index for Multi-dimensional Objects[OL].http://repository.cmu.edu/cgi/viewcontent.cgi?article=1563&context=compsci,2015 |
| [6] | Beckmann N, Kriegel H P, Schneider R, et al. The R*-tree:an Efficient and Robust Access Method for Points and Rectangles[J]. ACM, 1990,19(2):322-331 |
| [7] | Kamel I, Faloutsos C. Hilbert R-tree:An Improved R-tree Using Fractals[OL]. http://drum.lib.umd.edu/handle/1903/5366,1993 |
| [8] | Kothuri R K V, Ravada S, Abugov D. Quadtree and R-tree Indexes in Oracle Spatial:A Comparison Using GIS Data[C]. The 2002 ACM SIGMOD International Conference on Management of Data, Wisconsin, USA,2002 |
| [9] | Guo Jing, Guo Wei, Hu Zhiyong. QR-tree:An Efficient Spatial Indexing Structure for GIS with very Large Spatial Database[J]. Geomatics and Information Science of Wuhan University, 2003, 28(3):306-310(郭菁,郭薇,胡志勇. 大型空间数据库的有效索引结构QR-树[J]. 武汉大学学报·信息科学版,2003, 28(3):306-310) |
| [10] | Fu Y C, Hu Z Y, Guo W, et al. QR-tree:a Hybrid Spatial Index Structure[C]. Machine Learning and Cybernetics, 2003 International Conference, Xi'an, China, 2003 |
| [11] | Qiu Jianhua, Tang Guobing, Huang Huaguo. An Index Structure Based Quad-tree and R*-tree-QR*-tree[J]. Computer Applications, 2003, 23(8):124-126(邱建华, 唐学兵, 黄华国. 一种基于四叉树和R*-树的索引结构——QR*-树[J]. 计算机应用, 2003, 23(8):124-126) |
| [12] | Huang Ming, Chen Zhe. Research on the Spatial Index Based on Improvement QR Tree[J]. Journal of Heilongjiang Institute of Technology, 2005, 19(3):18-20(黄明, 陈哲. 基于改进QR-树的空间数据索引的研究[J]. 黑龙江工程学院学报, 2005, 19(3):18-20) |
| [13] | Zhao Nan, Hao Zhongxiao. A Hybrid Structure of Spatial Multilevel Index Based on Grids and R-Tree[J].Computer Technology and Development, 2009, 19(3):91-94(赵楠, 郝忠孝. 一种基于网格与R树的多级混合索引[J]. 计算机技术与发展, 2009, 19(3):91-94) |
| [14] | Zhao Lingli, Zhao Renliang, Zhu Jianjun,et al. A Data Integration Hiberarchy Index Tree Oriented to Urbanization System[J]. Geomatics and Information Science of Wuhan University, 2010, 35(12):1486-1490(赵伶俐, 赵仁亮, 朱建军, 等. 一种面向城镇化系统数据整合的层次索引树[J]. 武汉大学学报·信息科学版, 2010, 35(12):1486-1490) |
| [15] | Bi Yuekun, Liu Pengju, Li Chunqiu. R-tree-based Maritime Mobile Ad Hoc Networks Spatial Index[J]. China Water Transport, 2013,9:64-65(毕月琨, 刘鹏举, 李春秋. 基于R树的海上移动自组网空间索引[J]. 中国水运, 2013,9:64-65) |
| [16] | Tan Wenken, Wang Changhon,Shi Yishao. Digital Underground Spatial Indexing QR-tree Based on XML[J]. Journal of Zhejiang University(Engineering Science), 2009,9:1615-1620(谭文垦, 王长虹, 石忆邵. 基于XML的数字地下空间索引QR树研究[J]. 浙江大学学报:工学版, 2009,9:1615-1620) |
| [17] | Cheng Chengqi, Ren Fuhu, Pu Guolian, et al. Introduction to Spatial Information Subdivision Organization[M].Beijing:Science Press, 2012(程承旗,任伏虎,濮国梁,等. 空间信息剖分组织导论[M]. 北京:科学出版社,2012) |
| [18] | Li Deren, Zhu Xinyan, Gong Jianya. From Digital Map to Spatial Information Multi-grid-A Thought of Spatial Information Multi2grid Theory[J]. Geomatics and Information Science of Wuhan University, 2004, 28(6):642-650(李德仁, 朱欣焰, 龚健雅. 从数字地图到空间信息网格——空间信息多级网格理论思考[J]. 武汉大学学报·信息科学版, 2004, 28(6):642-650) |
| [19] | Song Shuhua, Cheng Chengqi, Guan Li, et al. Analysis on Global Geodata Partitioning Models[J]. Geography and Geo-information Science, 2008, 24(4):11-15(宋树华, 程承旗, 关丽, 等. 全球空间数据剖分模型分析[J]. 地理与地理信息科学, 2008, 24(4):11-15) |
| [20] | Jin An, Cheng Chengqi. Spatial Data Coding Method Based on Global Subdivision Grid[J]. Journal of Geomatics Science and Technology, 2013, 30(3):284-287(金安, 程承旗. 基于全球剖分网格的空间数据编码方法[J]. 测绘科学技术学报, 2013, 30(3):284-287) |
 2016, Vol. 41
2016, Vol. 41



