
文章信息
- 吴明光, 郑培蓓, 邓国臣, 崔登吉, 崔丽丽
- WU Mingguang, ZHENG Peibei, DENG Guochen, CUI Dengji, CUI Lili
- 线对象V-O分解与符号化算法
- V-O Tessellation: An Algorithm for Polyline Symbolization
- 武汉大学学报·信息科学版, 2016, 41(3): 421-426
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 421-426
- http://dx.doi.org/10.13203/j.whugis20140173
-
文章历史
- 收稿日期: 2014-09-11

2. 中国测绘科学研究院, 北京, 100830
2. Chinese Academy of Surveying&Mapping, Beijing 100830, China
线状符号用来表达地理空间上沿某个方向延伸的线状或带状现象的地理要素,如河流、道路、国界线等[1]。线符号绘制的难点可以归结为以下两点。
(1) 符号绘制算法复杂。SLD(styled layer descriptor)将线符号定义为Solid-color、GraphicFill、GraphicStroke等3种基本线型[2]。此外,还包括粗细渐变的符号[3]和颜色渐变的符号[4]。实施上述线型绘制时,涉及子像素级的图形、图像绘制处理[5]。
(2) 符号绘制效率低。一方面,影响用户体验,难以支持全景式GIS应用[6],限制了手机、PDA等设备(CPU低、内存小、电池供电能力弱和显示屏幕小) 上高质量矢量地图应用[7, 8];另一方面,难以支持动态制图[9, 10, 11]。
硬件加速的地图绘制已成为发展趋势之一[12, 13]。Google公司推出WebGL地图,开源地图发布平台MapServer支持OpenGL地图绘制。本文面向硬件加速的地图绘制,以线符号绘制作为研究对象,首先对5种典型线对象分解与绘制方法进行比较研究,在此基础上提出了一种新的线对象分解与符号绘制方法。
1 典型线分解与绘制算法分析如何将线对象实施分解成为符号化的关键问题,除算法复杂度外,算法结果的评价指标还包括剖分后顶点、三角形以及三角形条带的个数[13]。典型线分解与绘制算法主要包括以下5种。
1.1 基于Minkowski和(Minkowski sum)原理的分解绘制若a为由3个节点构成的一个线对象,b为一个半径为r的圆形。对a、b的Minkowski sum[14]进行着色处理,即可得到a对象半径为r的绘制结果。但其缺点如下:① b沿着a移动时的步长过大,会导致图形边缘出现锯齿甚至露白,而步长过小,则重复覆盖过多,绘制效率不高。② 无法支持宽度渐变、颜色渐变的线型,也难以支持线对象的纹理填充。
1.2 矩形-圆分解绘制先将线对象以两个节点为单位,分解为由两个相邻节点构成的线段。将线段左、右平移r得到一个矩形。线段相交的地方叠加绘制一个半径为r的圆形[15]。该方法绘制效率高,视觉上能够满足要求。但该方法存在以下问题:① 当颜色指定了透明度后,拐点处将出现重绘和漏绘区域。纹理贴图的情况下也会出现重叠线型。② 适用于纯色填充的线绘制,不支持纹理线、渐变线。③ 无法直接实施反走样。
1.3 梯形分解绘制先得到线对象的扩展多边形。将扩展多边形的顶点按照y坐标由小到大排序,在不同y坐标处引一条平行于x轴的平行线。所有的平行线将扩展多边形分解为一系列梯形(梯形可退化为三角形)[16]。对梯形进行绘制即可得到半径为r的线。
该算法可扩充多边形的外推算法,可支持纹理映射、渐变线型等;不会出现重绘、漏绘现象。但该方法在梯形分解时,需要涉及内外判别和排序等算法,算法复杂度高;支持Round Cap或者Round Join时,外推多边形分解得到的梯形数量大,三角形条带个数较多,绘制效率不高;不直接支持反走样。
1.4 整体纹理映射绘制首先生成线对象的扩展多边形。将一个实施了反走样后的直线(栅格)作为纹理,计算扩展多边形顶点的纹理坐标,将扩展多边形整体进行纹理映射[13]。其优点是:① 支持反走样,支持线的Cap样式控制,绘制效率较高。② 该算法绘制平行线时考虑到宽度,可支持渐变线的绘制。该方法存在的问题是:颜色的修改与渐变,反走样的开关均需要纹理的切换,需要额外的纹理管理,且资源占用较大。
1.5 V分解绘制对于任意线对象,沿着坐标点的顺序,除首末点外,计算任意相邻两个节点的中点(内插点)。内插点-顶点-内插点构成一个V型的折线。线对象每个顶点均可以指定颜色和宽度值。本文将内角方向的顶点平移计算称为内推,相应的点称为内推点;反之,成为外推和外推点。以V为单位,可以构建一个三角形条带或者三角形扇。每个三角形的顶点均包含颜色值,支持颜色渐变线。每个节点可以指定宽度,支持宽度渐变线[17]。该方法存在的问题是:① 在计算扩展多边形时,当线段角度较小且线的宽度较大时,顶点的内推点可能并不存在,无法完成V的三角剖分。② 用于反走样的扩展多边形的计算是以V为单位的,彼此独立,存在节点冗余,三角化剖分后,三角形过多,三角形条带数量大,绘制效率不高。
综合以上5种典型线对象分解与绘制算法来看,V分解算法能够支持颜色线、纹理线、渐变线的绘制,反走样效果好。本文在V分解算法的基础上,针对其存在的两个问题,提出了一种V-O分解与绘制方法。
2 线对象的V-O分解算法 2.1 线对象的V分解与文献[17]相同的是,对线对象采用V分解。为论述方便,将内推线的交点称为内点PI,将外推线的交点称为外点PO。若采用圆形拐角样式,则外点有多个。
如图 1所示,设有Pi-1、Pi、Pi+1构成一个V单元。Pi-1、Pi的内推线为P1P2,Pi、Pi+1的内推线为P3P4。设P1P2与P3P4的交点为x、y。依据解析几何原理,有:
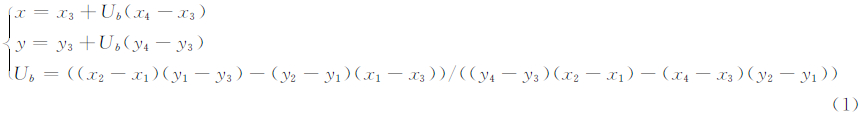

|
| 图 1 内推线计算示意图 Fig. 1 Schematic Diagram of Interpolated Line Calculation |
若Ub < 0,则P1P2与P3P4在线段内部没有交点,交点在P3外侧(x < x3)。若Ub >1,则P1P2与P3P4在线段内部没有交点,交点在P4外侧(x > x4)。只有当0≤Ub≤1时,交点位于P3、P4之间(包括两个端点)。同理可分析x、y与P1P2的关系。理论上,x、y与P1P2、P3P4存在3×3种情况。为简化分析,将Pi-1、Pi之间的距离定义为1,将Pi+1、Pi之间的距离定义为d,Pi-1、Pi、Pi+1之间的夹角定义为θ,线段的宽度为2*w,则有:
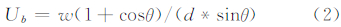
在内推情况下,0°< θ <180°。由式(2)可知,Ub >0,所以不存在x < x3的情况。同理可知,不存在x > x2的情况。因此,P1P2与P3P4所有可能不相交的情况只有如表 1所示的3种,对应的图形如图 2所示。

|
| 图 2 P1P2与P3P4三种不相交的情况 Fig. 2 Three Situations of P1P2 and P3P4 Without Intersecting |
| x < x3 | x3≤x≤x4 | x > x4 | |
| x < x1 | 不存在 | 不相交 | 不相交 |
| x1≤x≤x2 | 不存在 | 相交 | 不相交 |
| x > x2 | 不存在 | 不存在 | 不存在 |
图 3(a)为P0P1P2构成的一个V单元,每个顶点可以分别赋颜色和宽度值。然后分别依据3个顶点的宽度,计算P0P1、P1P2的外推线P3P4、P9P10和内推线P5P6、P7P8。文献[18]的方法不适用所有内推线不相交的情况。本文给出内推线三种相离情况的统一处理方式:以P1为中心点,依据P6、P5、P0、P3、P4、PO1、PO2、…、PON、P9、P10、P0、P8、P7为顶点,构造三角形扇。三角形分解情况如图 3(d),其绘制结果如图 3(e)。改进后的V分解方法能够适用于不同线目标。

|
| 图 3 线对象的V分解与绘制 Fig. 3 The Schematic Diagram of V Decomposition and Drawing of Polyline |
为实施反走样,文献[16]的方式是:对线对象实施V分解,对其产生的坐标点,两两为单位,生成线段的平行线,然后构造梯形,连接梯形的对角线来实施三角剖分。但其主要问题如下:① 三角形过多,生成2(n-2)个独立的三角形条带,绘制效率不高;② 依然存在内点不存在的问题,无法构造平行线。
顶点、三角形、三角形条带个数是三角剖分的3个重点评价指标。从三角形条带和三角形扇的数据结构容易看出,相邻的两个三角形条带是可以合并的:位置相同的两个顶点可以合并两个三角形,条带可以合并为一个三角形条带。如果两个三角形扇的起始点不一致,则无法合并。本文方法是对每个V分解的单元生成可合并的三角形条带。其详细描述如下。
1) 线段的中点除外,顶点内、外推。内、外推的距离就是反走样的单位。对于内点不存在的情况下,又分为两种情况,新的内推线有交点,则将该交点重复记录。如果没有交点,对两条内推线的末点进行外推,得到两个外推点。这样得到两两配对的坐标点。
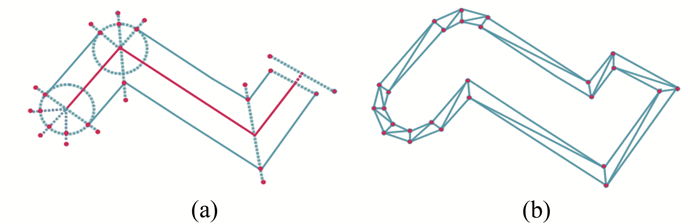
2) 依次构建V分解单元的外推点对和内推点对,如图 4(a)。
|
| 图 4 线对象的O分解 Fig. 4 The O Decomposition of Polyline |
3) 按照结点顺序,依次连接左外推点对,到末点后,按照节点逆序,依次连接右内推点。首尾相连,构成一个封闭的环形如图 4(b),称之为O。
改进后的O分解绘制方法,在扩展多边形生成时,跳过了V分解时内插的n-3个中间点,提高了计算效率;跳过中间点后,三角化时三角形的个数也相应减少了2(n-3)个,可有效减少反走样时的内存/显存的资源占用;在Round、Square Cap的情况下,用于反走样绘制的O完全包含了线对象。在Butt Cap情况下,O中包含了4个面积为0的三角形。两种情况下,O分解均能够将三角形条带个数由 2(n-2)降为1。
2.3 基于线对象的V-O分解的地图符号基本线型绘制本文将线对象的基本线型绘制分为线的材质(颜色或者纹理)、线的形状(等宽线或者渐变线)以及反走样。O分解后,反走样绘制方法与文献[16]相同。不同材质与形状的线绘制方法描述如下:
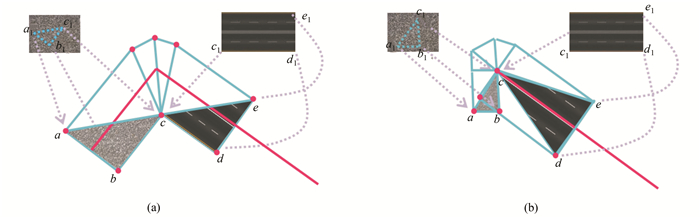
对于纹理线的绘制,本文方法支持线性填充纹理与平行填充纹理。如图 5所示,本算法分顶点的内推点存在与否两种情况讨论。内推点存在时,以该点为中心,构造三角形扇。若为平行填充,则直接由顶点坐标得到纹理坐标,如图 5(a)中的a、b、c顶点的纹理坐标a1、b1、c1。若为线性填充,则将顶点坐标线性变换后得到纹理坐标,如图 5(a)中的c、d、e顶点的纹理坐标c1、d1、e1。内推点不存在时,则以V的中间点为中心,构造三角形扇。若为平行填充,则直接由顶点坐标得到纹理坐标,如图 5(b)中的a、b、c顶点的纹理坐标a1、b1、c1。若为线性填充,则将顶点坐标线性变换后得到纹理坐标,如图 5(b)中的c、d、e顶点的纹理坐标c1、d1、e1。采用类似纹理赋值的方法,可以实现颜色渐变。
|
| 图 5 V-O分解的纹理映射方法 Fig. 5 The Texture Mapping for V-O Decomposition |
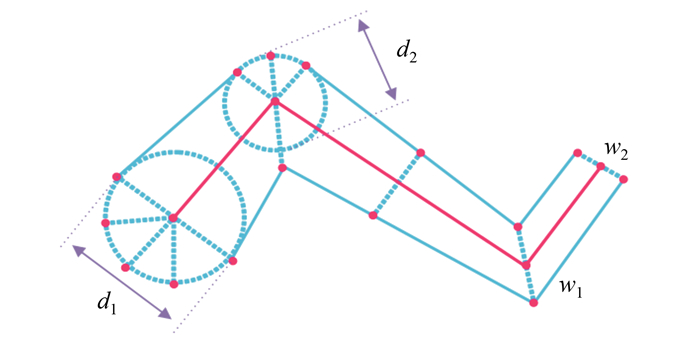
本文方法支持等宽线与变宽线的绘制。如图 6所示,线对象的V分解后,每个顶点均包含宽度信息。在生成扩展多边形时,可以逐点控制线的宽度d1、d2、w1、w2。若所有顶点的宽度相同,则为等宽线。若节点宽度不同,即为变宽线。
|
| 图 6 基于V-O分解的线宽控制示意图 Fig. 6 Width Control Based on V-O Decomposition |
本文选择某地区一条复杂境界数据(包含487个点)进行效率测试。实验中采用C++语言实现本文算法,采用OpenGL作为图形绘制接口。测试环境:IBM ThinkPad T410s,Inter(R) core(TM)i5 CPU,3 GB 内存,Windows 7 32位操作系统。将境界数据按照8个像素为单位进行分解与绘制。绘制结果如图 7。由图 7(a)可知,Vase Render在角度较小和线段距离较近的地方出现了绘制错误。由于完善了V分解算法,本文算法能够正确地进行三角剖分,如图 7(b)。叠加两个宽度的纯色填充绘制结果,绘制了高速公路,如图 8(a);采用线性纹理填充绘制了真实感的道路,如图 8(b);采用平行纹理映射,绘制了真实感的石质道路,如图 8(c);采用透明的线性纹理填充,绘制了背斜,如图 8(d);采用宽度渐变填充,绘制了河流,如图 8(e);同时采用宽度和颜色渐变,绘制了河流,如图 8(f)。可见,本文算法能很好地支持各种地图符号的基本线型。

|
| 图 7 算法适应性测试结果 Fig. 7 Adaptability Test Result of This Algorithm |

|
| 图 8 算法对各种基本线型的支持 Fig. 8 The Basic Polyline Styles Supported by This Algorithm |
为验证本文方法的效率,将本文算法与外推多边形的直接三角分解、外推多边形的梯形分解以及V分解作为效率对比分析。三角形分解采用GLU中的tessellation函数。采用8、12像素宽度来对前述境界数据进行符号绘制,并对比Vase Render与本文方法反走样的效率。每次循环绘制100次,运行10次,取平均值作为测试结果,实验结果如表 2所示。
| 梯形分解 | 三角形分解 | V-O不反走样 | Vase Render反走样 | V-O反走样 | |
| 1 | 892 | 1 584 | 253 | 462 | 348 |
| 2 | 1 067 | 1 702 | 322 | 485 | 417 |
由表 2可知,V分解和V-O分解绘制的效率要明显优于梯形分解和直接三角形分解。其主要原因是:V分解和V-O分解在分解过程中,保留了线对象的结构信息,一个V对象可以直接分解为一个三角形条带。对于反走样绘制,V-O分解中,由于避免了中间内插节点的外推,扩展多边形的顶点数据、三角形的个数、三角形条带的个数均小于V分解,所以能够明显地提高反走样绘制的效率。
4 结 语线对象符号化的效率与质量成为当前地图制图与发布的关键因素[19]。硬件加速绘制成为当前的研究热点[20]。本文分析比较了5种典型线对象分解与绘制方法,在V分解的基础上提出一种新型的线符号绘制方法。其对于V分解的主要改进包括以下方面。
1) 分析了线段内推线不相交的8种情况,通过理论分析,排除了三角剖分情况下不可能存在的5种情况,对可能存在的3种情况,给出了统一处理方式,提高了V分解方法的适应性。
2) 基于邻近三角形条带的可合并性分析,提出了面向反走样绘制的扩展多边形构建和绘制方法。避免中间点内插,提高了构建效率,减少了资源占用。通过邻近三角形条带的合并,将三角形条带的个数减至1,能够显著提高线对象绘制效率。
实验表明,本文提出的V-O分解方法,提高了V分解后三角化的适应性,减少了顶点、三角形以及三角形条带的个数,能够支持颜色线、纹理线、渐变线等基本线型的绘制,支持反走样。本文方法具有较强的适应性和绘制效率。
| [1] | Robinson A C, Pezanowski S, Troedson S. Symbol Store: Sharing Map Symbols for Emergency Management[J]. Cartography and Geographic Information Science,2013, 40(5):415-426 |
| [2] | Lalonde W. Styled Layer Descriptor Implementation Specification 1.0.0[Z]. OGC Document, England,2002 |
| [3] | Li Li, Wang Jiechen, Shen Dingtao. A Method for Plotting Gradual Change Symbol of Single-line Stream[J]. Bulletin of Surveying and Mapping, 2008(11): 64-67(李丽,王结臣,沈定涛,等. 一种单线河流渐变符号的绘制方法[J]. 测绘通报, 2008(11): 64-67) |
| [4] | Maceachren A M. How Maps Work:Representation, Visualization and Design[M]. Guilford: Guilford Press, 2004 |
| [5] | Wu Xiaofang, Du Qingyun. Design and Algorithm Optimization of Complex Linear Symbol[J]. Geomatics and Information Science of Wuhan University, 2006,31(7):632-635(吴小芳,杜清运. 复杂线状符号的设计及优化算法研究[J]. 武汉大学学报·信息科学版, 2006,31(7):632-635) |
| [6] | Longley P A, Goodchild M F, Maguire D J, et al. Geographic Information System and Science[M]. England:John Wiley & Sons, Ltd,2010 |
| [7] | Akenine-M Ller T, Ström J. Graphics for the Masses: A Hardware Rasterization Architecture for Mobile Phones[C]. ACM SIGGRAPH,San Diego,2003 |
| [8] | Noguera J M, Segura R J, Ogáyar C J, et al. A Scalable Architecture for 3D Map Navigation on Mobile Devices[J]. Personal and Ubiquitous Computing,2013, 17(7): 1 487-1 502 |
| [9] | Zhu Guorui, Xu Zhiyong, Wu Xiaofang. Design of Dynamic Map Symbol Based on Muli-transform Assembly[J]. Geomatics and Information Science of Wuhan University, 2006,32(6):548-551(祝国瑞, 徐智勇,吴小芳. 基于多重变换组合的动态地图符号设计[J]. 武汉大学学报·信息科学版,2006,32(6):548-551) |
| [10] | Ferreira N, Poco J, Vo H T, et al. Visual Exploration of Big Spatio-Temporal Urban Data: A Study of New York City Taxi Trips[J]. IEEE Trans Vis Comput Graph, 2013, 19(12): 2 149-2 158 |
| [11] | Zhang C, Li W. The Roles of Web Feature and Web Map Services in Real-Time Geospatial Data Sharing for Time-Critical Applications[J]. Cartography and Geographic Information Science,2005, 32(4): 269-283 |
| [12] | Renhart Y. Fast Map Rendering for Mobile Devices[OL]. http://gupea.ub.gu.se/bitstream/2077/24577/1/gupea_2077_24577_1.pdf,2014 |
| [13] | Lukas R. Rendering Interactive Maps on Mobile Devices Using Graphics Hardware [OL]. http://www.cg.tuwien.ac.at/research/publications/2012/ROESSLER-2012-OGLES/ROESSLER-2012-OGLES- thesis.pdf, 2012 |
| [14] | Packard K. A Realistic 2D Drawing System, 2003[OL]. http://www.keithp.com, 2003 |
| [15] | Wang Jiecheng, Cui Can, Pu Yingxia. A Novel Algorithm of Buffer Construction Based on Run-Length Encoding[J]. The Cartographic Journal, 2010, 47(3): 198-210 |
| [16] | Kilgard M J, Bolz J. GPU-Accelerated Path Rendering[J]. ACM Transactions on Graphics (TOG), 2012, 31(6): 172-179 |
| [17] | Github Inc. VASE Renderer is a Polyline and Curve Renderer on OpenGL[OL]. http://github.com/tyt2y3/vaserenderer,2014 |
| [18] | Tsang H F. Drawing Polylines by Tessellation[OL]. http://www.codeproject.com/Articles/226569/Drawing-polylines-by-tessellation, 2014 |
| [19] | Su Kehua, Zhu Xinyan, Gong Jianya. Cross-Platform Versatile Technology for GIS Symbols[J]. Geomatics and Information Science of Wuhan University,2009, 34(5):611-614(苏科华,朱欣焰,龚健雅. GIS符号的跨平台通用技术研究[J]. 武汉大学学报·信息科学版,2009,34(5):611-614) |
| [20] | RICE Daniel. OpenVG specification version 1.0.1[EB/OL]. http://www.khronos.org/files/openvg-quick-reference-card.pdf, 2006-01-26 |
 2016, Vol. 41
2016, Vol. 41




