文章信息
- 高孝杰, 简季, 戴晓爱, 陈婉佳
- GAO Xiaojie, JIAN Ji, DAI Xiaoai, CHEN Wanjia
- 基于Fréchet距离的光谱曲线匹配应用分析
- Spectral Curve Matching Application Analysis Based on Fréchet Distance
- 武汉大学学报·信息科学版, 2016, 41(3): 408-414
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 408-414
- http://dx.doi.org/10.13203/j.whugis20140147
-
文章历史
- 收稿日期: 2014-09-17

在遥感应用中,高光谱遥感已经成为非常重要的观测手段,其优势在于能够获取地物的连续光谱曲线,提供更全面的地物信息。成像光谱技术的问世,将由物质成分决定的地物光谱与反映地物存在格局的空间影像完整地结合起来,实现了人们认识论中逻辑思维和形象思维的统一,大大提高了人们对客观世界的认知能力[1]。利用高光谱图像进行地物分类也比传统多光谱分类精度更高,分类更细[1]。通常利用高光谱图像进行地物识别和分类主要是通过辐射定标、大气校正等图像预处理之后,将图像中的每个像元的光谱曲线进行提取,与地面实测地物的光谱曲线进行匹配,进而识别地物[1]。目前,应用最广的是利用高光谱图像进行矿物识别和提取,这是由于矿物的光谱曲线具有相对较大的差异性,而且不同的矿物质的反射光谱差异也很大,因此,可以精确定量地识别出矿体含有的不同矿物质[2, 3, 4]。
高光谱图像在植被遥感应用中也非常广泛[5, 6, 7],在针对不同植物的识别和分类应用中,难点在于不同植被的反射光谱曲线,特征波段比较集中,差异不明显,尤其是绿色植物,不同绿色植物类型之间具有差异往往表现在反射率的高低。针对这类问题,目前也有学者采取了不同的解决方法,取得了较好成果[8, 9]。很多算法都直接或间接用到了度量不同种类植物光谱曲线相似性的方法来区分物种[10]。光谱曲线相似性的度量问题,实际上是一种判别分析问题。对类别的相似性进行度量的指标为“距离”,通过计算曲线之间的距离,衡量两曲线类型之间的相似性。
很多学者在光谱曲线匹配的应用中利用过欧氏距离[11, 12, 13, 14]。欧氏距离是一种整体的差异和,用它来度量光谱曲线相似性时,计算过程中并没有充分考虑每一个特征点,而是整体考虑所有点之间距离的差异,通过求和的方法计算出总的差异,这就造成了欧氏距离对光谱曲线的特征波段的位置信息并不敏感,曲线类型识别精度不高。
有学者利用Hausdorff距离进行曲线相似性度量,并且证明了采用Hausdorff距离在一定程度上优于传统的光谱角距离(SAM)和光谱信息散度(SID)等方法[15]。Hausdorff距离是一个点集中的点到另一个点集中距该点最邻近点的距离组中的最大距离[16]。Hausdorff距离相较于欧氏距离虽然多考虑了点所在的位置问题,但是当把所有的点连接成曲线时,Hausdorff距离并没有考虑到曲线走势,虽然已经被应用于很多曲线相似性计算问题,但是当曲线走势不同时,Hausdorff距离并不能很好地判断相似度[17]。
本文提出了一种基于Fréchet距离的度量光谱曲线相似度的一种新方法,该方法不仅充分考虑了曲线上点的位置信息,同时考虑了整体曲线的走势问题。将Fréchet距离应用于植物实测光谱数据的物种识别,取得了较好的效果。
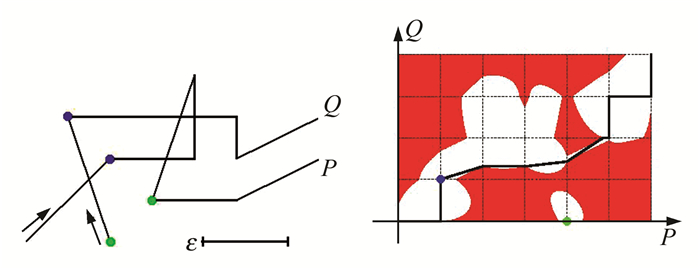
1 基于Fréchet距离的光谱曲线匹配Fréchet 距离由法国数学家 Fréchet提出,这是一种将曲线以固定方向重参数化来计算距离的方法[17]。该方法的一个形象的描述如下:假设一个人牵着一条狗散步,在同一个时间段内,人和狗都能够自由控制各自的行进速度和行走路线(但规定只能前进,不允许倒退),人和狗各自走过的路线为两条曲线,Fréchet距离就是人和狗之间走过这两条曲线需要的最小绳长。一般定义如下:
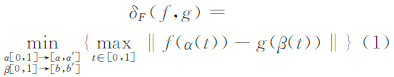
式中,f:[α,α']→V;g:[b,b']→V为连续映射;V表示连续空间;α、α',b、b'为实数,且α<α',b<b';t为时间;α、β为连续非减函数,α(0)=α,α(1)=α';β(0)=b,β(1)=b'。可见,Fréchet距离是连续曲线之间的距离,考虑了曲线的走向,计算时需要从所有可能的α、β函数中,找出一对α(t)、β(t)使得遍历两条曲线时,两条连续曲线之间的连通距离最短。直接求解时,显然这是一个非确定多项式问题,而要让计算机在多项式时间求解出结果,需要在计算方面做一些变化。许多学者针对不同的方面对Fréchet距离的求解问题提供了各自的方案[17, 18, 19]。
本文采用文献[17]提出的Fréchet距离求解方案。如图 1所示,如果有一条单调曲线从这个二维空间的左下角的点(0,0)通过自由空间连通到右上角的点(p,q),这时的最小ε值就是所要计算的Fréchet距离[19]。P、Q是由离散点连成的曲线,p、q分别是P、Q曲线的离线点个数,ε为大于0的实数,ε越大,自由空间就越大,就更有可能连通。将Fréchet距离的计算问题转化为求解最小ε的问题,并且计算能够在多项式时间内完成。
2 实验数据与结果分析 2.1 数据采集与处理本文使用ASD地物光谱测量仪分别对银杏、雪松、三颗针、桂花和冬青等5种植物进行了光谱测量。分别采摘每种植物类型6个不同地点的不同个体的叶片,并在同一外界条件下进行测量,以减少由于外界环境和光照条件等对测量结果造成的误差,每个样本个体测得9条样本光谱曲线。例如:对银杏叶片进行测量时,分别采摘6个不同银杏个体的叶片进行测量,每个银杏叶片个体测得9条不同的光谱曲线测量值,就得到类型为银杏的样本光谱曲线一共54条。这样对每一种植物类型的叶片进行测量,每种植物类型都测得54条样本光谱曲线。
得到了这些样本光谱曲线之后,随机选择每个物种测量数据总量的5/6计算出该物种的一条“相对标准光谱曲线”(下文简称“标准曲线”),这样可以得到每个物种的标准曲线(实际应用中可以使用标准光谱库中的物种光谱曲线代替)。将每个测量数据总量的其余1/6作为测试样本曲线,用于测试算法识别精度。即将每个物种的54条光谱曲线分成两类,9条曲线作为测试曲线,将另外45条曲线用来求物种的标准曲线。本文在数据处理时主要采用了以下两个方法:① 为了去除测量时水汽的影响,只取植物特征波段,所有光谱曲线只保留500~1 200 nm范围内光谱数据;② 为了进一步减少误差,在求物种“相对标准光谱曲线”时,按照“取中间平均,去两边数据”的办法,对每个物种的样本数据进行排序,舍弃前后20%的数据,只将中间80%的数据进行平均计算。这样去掉了离均值较远的测量值,有效地避免了误差较大的测量值对平均后的相对真实值的影响。
对每个物种的光谱曲线数据进行上述处理之后,得到每个植物类型1条标准曲线和9条测试样本曲线。
2.2 光谱曲线识别经过数据处理之后共得到了5条标准曲线和45条测试样本光谱曲线。分别用每个物种的9条测试样本光谱曲线与其对应的标准曲线进行Fréchet距离的计算,算法所计算出的距离值,与测试样本光谱曲线距离最小的标准曲线,即相似性最大的标准曲线所对应的物种类型作为算法识别的类型值。通过算法正确识别的类型个数除以总的样本个数得到本次实验识别精度(注:本实验由于样本种类较少,算法识别的精度只能作为相对参考,并不代表绝对精度)。
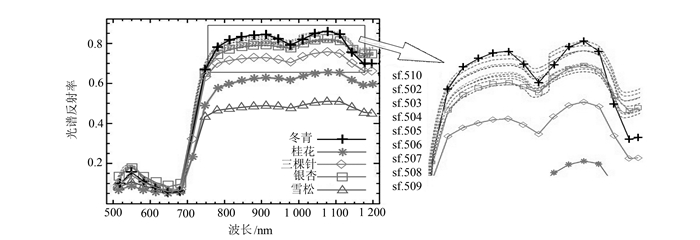
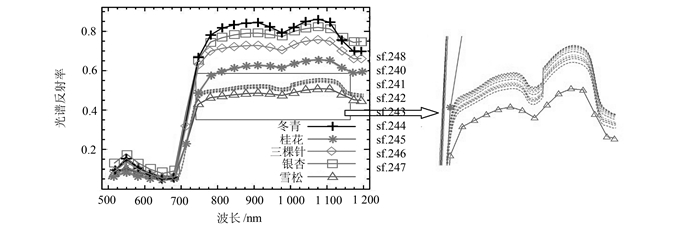
2.3 结果分析数据经过处理后,得到的5个物种标准曲线和每组测试样本曲线分别如图 2~图 6所示,判别结果分别如表 1~表 5所示,其中银杏、雪松、三颗针、桂花、冬青为特殊标记曲线,其余曲线表示测试样本曲线。
|
| 图 2 银杏测试样本曲线 Fig. 2 Test Sample Curve of Gingko |
|
| 图 3 雪松测试样本曲线 Fig. 3 Test Sample Curve of Cedar |
|
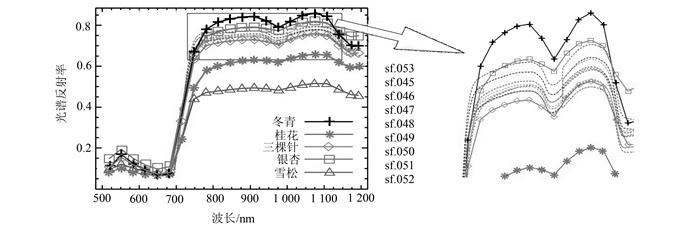
| 图 4 三颗针测试样本曲线 Fig. 4 Test Sample Curve of Barberry |
|
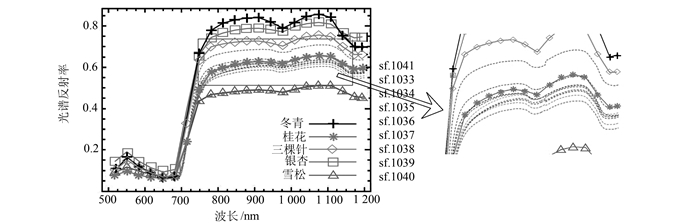
| 图 5 桂花测试样本曲线 Fig. 5 Test Sample Curve of Osmanthus |
|
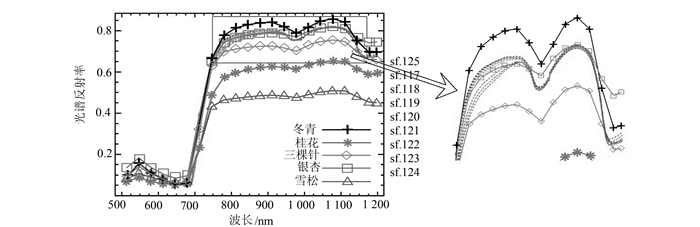
| 图 6 冬青测试样本曲线 Fig. 6 Test Sample Curve of Holly |
| 测试类型 | 标准类型 | sf.510 | sf.502 | sf.503 | sf.504 | sf.505 | sf.506 | sf.507 | sf.508 | sf.509 | 识别精度 |
| 冬青 | 0.063 | 0.109 | 0.103 | 0.098 | 0.091 | 0.079 | 0.074 | 0.075 | 0.068 | ||
| 桂花 | 0.185 | 0.185 | 0.187 | 0.189 | 0.206 | 0.218 | 0.196 | 0.204 | 0.203 | ||
| 银杏 | 三颗针 | 0.078 | 0.066 | 0.071 | 0.097 | 0.089 | 0.089 | 0.072 | 0.072 | 0.069 | |
| 雪松 | 0.285 | 0.269 | 0.270 | 0.271 | 0.272 | 0.275 | 0.278 | 0.279 | 0.281 | ||
| 银杏 | 0.031 | 0.040 | 0.039 | 0.041 | 0.034 | 0.047 | 0.035 | 0.034 | 0.035 | 100% |
| 测试类型 | 标准类型 | sf.248 | sf.240 | sf.241 | sf.242 | sf.243 | sf.244 | sf.245 | sf.246 | sf.247 | 识别精度 |
| 冬青 | 0.310 | 0.313 | 0.315 | 0.314 | 0.313 | 0.311 | 0.309 | 0.305 | 0.308 | ||
| 桂花 | 0.198 | 0.152 | 0.132 | 0.132 | 0.114 | 0.103 | 0.133 | 0.123 | 0.126 | ||
| 雪松 | 三颗针 | 0.265 | 0.303 | 0.286 | 0.257 | 0.263 | 0.257 | 0.281 | 0.270 | 0.272 | |
| 雪松 | 0.030 | 0.049 | 0.048 | 0.047 | 0.045 | 0.042 | 0.038 | 0.036 | 0.034 | 100% | |
| 银杏 | 0.335 | 0.314 | 0.337 | 0.345 | 0.337 | 0.352 | 0.320 | 0.301 | 0.309 |
| 测试类型 | 标准类型 | sf.053 | sf.045 | sf.046 | sf.047 | sf.048 | sf.049 | sf.050 | sf.051 | sf.052 | 识别精度 |
| 冬青 | 0.065 | 0.072 | 0.073 | 0.073 | 0.071 | 0.070 | 0.068 | 0.064 | 0.064 | ||
| 桂花 | 0.110 | 0.128 | 0.145 | 0.153 | 0.173 | 0.187 | 0.174 | 0.183 | 0.182 | ||
| 三颗针 | 三颗针 | 0.025 | 0.075 | 0.058 | 0.028 | 0.030 | 0.024 | 0.032 | 0.030 | 0.045 | 89% |
| 雪松 | 0.222 | 0.206 | 0.207 | 0.209 | 0.210 | 0.212 | 0.216 | 0.217 | 0.219 | ||
| 银杏 | 0.092 | 0.080 | 0.102 | 0.110 | 0.102 | 0.116 | 0.086 | 0.099 | 0.116 |
| 测试类型 | 标准类型 | sf.1041 | sf.1033 | sf.1034 | sf.1035 | sf.1036 | sf.1037 | sf.1038 | sf.1039 | sf.1040 | 识别精度 |
| 冬青 | 0.166 | 0.183 | 0.181 | 0.180 | 0.178 | 0.175 | 0.172 | 0.166 | 0.165 | ||
| 桂花 | 0.078 | 0.025 | 0.022 | 0.025 | 0.043 | 0.055 | 0.029 | 0.038 | 0.037 | 100% | |
| 桂花 | 三颗针 | 0.140 | 0.221 | 0.204 | 0.175 | 0.177 | 0.170 | 0.179 | 0.171 | 0.181 | |
| 雪松 | 0.128 | 0.113 | 0.113 | 0.114 | 0.116 | 0.118 | 0.122 | 0.123 | 0.125 | ||
| 银杏 | 0.188 | 0.183 | 0.199 | 0.209 | 0.201 | 0.216 | 0.195 | 0.198 | 0.213 |
| 测试类型 | 标准类型 | sf.125 | sf.117 | sf.118 | sf.119 | sf.120 | sf.121 | sf.122 | sf.123 | sf.124 | 识别精度 |
| 冬青 | 0.077 | 0.062 | 0.056 | 0.048 | 0.046 | 0.048 | 0.048 | 0.062 | 0.070 | 78% | |
| 桂花 | 0.159 | 0.209 | 0.227 | 0.230 | 0.248 | 0.260 | 0.235 | 0.246 | 0.244 | ||
| 冬青 | 三颗针 | 0.094 | 0.058 | 0.073 | 0.114 | 0.105 | 0.103 | 0.092 | 0.102 | 0.087 | |
| 雪松 | 0.335 | 0.317 | 0.318 | 0.320 | 0.322 | 0.324 | 0.328 | 0.330 | 0.331 | ||
| 银杏 | 0.058 | 0.046 | 0.068 | 0.076 | 0.068 | 0.082 | 0.052 | 0.065 | 0.082 |
从图 2、图 4与图 6中可以看出,银杏、三颗针、冬青的光谱曲线在分布上极其相似,进行曲线识别时很容易将其混淆。但通过表 1可以看出,Fréchet距离银杏叶片样本与银杏标准曲线之间距离最小,也就是完全将银杏的光谱曲线与其他物种区分开来。结合表 3可以看到,在三颗针的测试样本中,仅有样本sf.045被错误地识别为冬青,其他样本仍然能正确的识别。表 5中的结果显示,仅有sf.125和sf.117这两个冬青样本被错误识别为银杏,其他样本识别都很准确。这说明Fréchet距离在度量曲线相似性时,充分考虑了每条曲线的走势,而不仅是曲线的分布与位置。本次实验中,雪松和桂花这两个物种在曲线分布和走势上与其他物种区分较好,仅有桂花sf.1041测试样本偏离其他桂花样本较远,如表 4所示,依然能被正确识别。
2.4 算法比较为了进一步分析Fréchet距离,本文针对冬青的光谱曲线分别作了欧氏距离和Hausdorff距离的分析。从表 6,表 7中可以看出,欧氏距离的相对识别精度为23%,欧氏距离几乎全部将冬青的测试样本错误识别为银杏。Hausdorff距离比欧氏距离效果较好,相对识别精度为67%,但是测试样本sf.125和sf.117 Hausdorff距离依然没有识别出来,测试样本sf.123与冬青标准曲线的距离等于它与银杏标准曲线的距离,无法判断其类型。
| 测试类型 | 标准类型 | sf.125 | sf.117 | sf.118 | sf.119 | sf.120 | sf.121 | sf.122 | sf.123 | sf.124 | 识别精度 |
| 冬青 | 1.091 | 0.903 | 0.862 | 0.875 | 0.901 | 0.922 | 0.945 | 1.038 | 1.067 | 23% | |
| 桂花 | 3.052 | 4.071 | 4.479 | 4.543 | 4.926 | 5.188 | 4.610 | 4.825 | 4.775 | ||
| 冬青 | 三颗针 | 1.638 | 0.972 | 1.242 | 1.907 | 1.765 | 1.827 | 1.491 | 1.671 | 1.509 | |
| 雪松 | 6.594 | 6.191 | 6.219 | 6.257 | 6.297 | 6.355 | 6.435 | 6.472 | 6.514 | ||
| 银杏 | 0.796 | 0.815 | 0.745 | 0.793 | 0.775 | 0.874 | 0.820 | 1.108 | 1.133 |
| 测试类型 | 标准类型 | sf.125 | sf.117 | sf.118 | sf.119 | sf.120 | sf.121 | sf.122 | sf.123 | sf.124 | 识别精度 |
| 冬青 | 0.006 | 0.004 | 0.003 | 0.002 | 0.002 | 0.002 | 0.002 | 0.004 | 0.005 | 67% | |
| 桂花 | 0.025 | 0.044 | 0.052 | 0.053 | 0.062 | 0.067 | 0.055 | 0.060 | 0.060 | ||
| 冬青 | 三颗针 | 0.009 | 0.003 | 0.005 | 0.013 | 0.011 | 0.011 | 0.009 | 0.010 | 0.008 | |
| 雪松 | 0.112 | 0.100 | 0.101 | 0.102 | 0.104 | 0.105 | 0.108 | 0.109 | 0.110 | ||
| 银杏 | 0.003 | 0.002 | 0.005 | 0.006 | 0.005 | 0.007 | 0.003 | 0.004 | 0.007 |
本文针对光谱曲线相似性的度量问题,提出了利用Fréchet距离进行植物光谱曲线相似性度量的方法,通过实际数据分析可以看出在光谱匹配实验中,该算法的精度较常用的距离算法有所提高,并且该算法对测量误差的包容性更强。然而,计算Fréchet距离的算法在数据量大的时候耗时太严重,这就限制了其应用范围,并不适用于对某些需要实时匹配识别的应用,但是诸如高光谱图像分类、地物目标识别等应用问题,其算法时间成本往往并不是最重要的因素,首要考虑的是精度问题,应用Fréchet距离分析光谱曲线的相似性问题可以得到较好的效果。
本文引入Fréchet距离解决了基本的光谱曲线匹配问题,但需要指出,不论是图像分类还是目标识别等应用,都涉及到不同的影响因素,比如辐射定标、光谱库建立、噪声去除、同物异谱、混合像元等等,本文下一步工作将继续探究算法在不同应用中的适用性。对算法效率方面的改进,重点就是压缩数据量,用尽量少的数据分析光谱特征。目前有很多办法可以压缩数据量保留特征信息,例如PCA、MNF、道格拉斯算法等,还有很多算法通过提取特征波段或者夸张不同物种之间特征波段的特征性来达到间接降维的目的,但是需要明确的是,虽然简化后数据量变小,算法所耗费的时间减少,但是这些简化算法对数据都有损失,对于会不会影响到光谱曲线的特征波段,以及对某些细节信息的保留的问题还有待进一步验证。并且很多算法并不是完全自动控制,算法中涉及的某些阈值需要人工设置,这又牵涉到经验问题。不同的阈值必然影响到简化后曲线的形态,很有可能会影响到算法的识别精度。因此,阈值的设置问题需要进一步深入研究。
| [1] | Tong Qingxi, Zhang Bing, Zheng Lanfen. Hyperspectral Remote Sensing[M]. Beijing:Higher Education Press,2006(童庆禧, 张兵, 郑兰芬. 高光谱遥感:原理、技术与应用[M]. 北京: 高等教育出版社, 2006) |
| [2] | Chang Ruichun. Application of Altered Mineral Information and Structure to Hyperspectral Remote Sensing Prospecting[J]. Scientific and Technological Management of Land and Resources, 2012(6):84-87(常睿春. 虫变矿物信息与构造在高光谱遥感找矿中的应用初探[J]. 国土资源科技管理, 2012 (6):84-87) |
| [3] | Yan Shouxun, Zhang Bing, Zhao Yongchao, et al. Summarizing the Technical Flow and Main Approaches for Discrimination and Mapping of Rocks and Minerals Using Hyperspectral Remote Sensing[J]. Remote Sensing Technology and Application,2004, 19(1):52-63(燕守勋, 张兵, 赵永超, 等. 高光谱遥感岩矿识别填图的技术流程与主要技术方法综述[J]. 遥感技术与应用, 2004, 19(1):52-63) |
| [4] | Xu Yuanjin, Hu Guangdao, Zhang Xian. Object Indentification for Hyperspectral Image Based on Exhaustive Method[J]. Geomatics and Information Science of Wuhan University, 2008,33(2):124-127(徐元进, 胡光道, 张献. 基于穷举法的高光谱遥感图像地物识别研究[J]. 武汉大学学报·信息科学版, 2008, 33(2):124-127) |
| [5] | Bao Gang. Hyperspectral Remote Sensing Estimation for the Vegetation Cover[J]. Journal of Nature Resources, 2013, 28(7):1 243-1 254 (包刚. 高光谱植被覆盖度遥感估算研究[J]. 自然资源学报,2013, 28(7):1 243-1 254) |
| [6] | Li Mingze, Zhao Xiaohong, Liu Yue, et al. Inversion of Vegetation Canopy's Chlorophyll Content Based on Airborne Hyperspectral Image[J]. Chinese Journal of Applied Ecology,2013, 24(1):177-182(李明泽, 赵小红, 刘钺, 等. 基于机载高光谱影像的植被冠层叶绿素反演[J]. 应用生态学报, 2013, 24(1):177-182) |
| [7] | Xin Liwei, Li Xiaojuan, Li Angsheng, et al. A Comparative Study on Estimation Model for Leaf Area Index of Vegetation in Marshes in Honghe National Nature Reserve Based on Hyperspectral and Multispectral Vegetation Indices[J]. Wetland Science,2013, 11(3):313-319(邢丽玮, 李小娟, 李昂晟, 等. 基于高光谱与多光谱植被指数的洪河沼泽植被叶面积指数估算模型对比研究[J]. 湿地科学,2013, 11(3):313-319) |
| [8] | Song S, Gong W, Zhu B,et al. Wavelength Selection and Spectral Discrimination for Paddy Rice, With Laboratory Measurements of Hyperspectral Leaf Reflectance[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2011, 66(5):672-682 |
| [9] | Zhang L, Huang X. Object-oriented Subspace Analysisfor Airborne Hyperspectral Remote Sensing Imagery[J]. Neurocomputing, 2010, 73(4/6):927-936 |
| [10] | Du Peijun, Tang Hong, Fang Tao. Algorithms for Spectral Similarity Measures in Hyperspectral RS[J]. Geomatics and Information Science of Wuhan University, 2006,31(2):112-115(杜培军, 唐宏, 方涛. 高光谱遥感光谱相似性度量算法与若干新方法研究[J]. 武汉大学学报·信息科学版, 2006, 31(2):112-115) |
| [11] | Fu X, Kim MS, Chao K, et al. Detection of Melaminein Milk Powders Based on NIR Hyperspectral Imaging and Spectral Similarity Analyses[J]. Journal of Food Engineering, 2014, 124:97-104 |
| [12] | Stein S, Scott D. Optimization and Testingof Mass Spectral Library Search Algorithms for Compound Identification[J]. J Am Soc Spectrom,1994, 5(9):859-866 |
| [13] | van der Meer F. The Effectivenessof Spectral Similarity Measures for The Analysis of Hyperspectral Imagery[J]. International Journal of Applied Earth Observation and Geoinformation,2006, 8(1):3-17 |
| [14] | Zhang J, Koo I, Wang B,et al. A Large Scale Test Dataset to Determine Optimal Retention Index Threshold Based on Three Mass Spectral Similarity Measures[J]. Journal of Chromatography A, 2012, 1 251:188-193 |
| [15] | Shi Beiqi, Liu Chun, Chen Neng, et al. Spectral Similarity Measure and Experimental Analyses for Field Spectroscopy[J]. Journal of Tongji University(Natural Science), 2011, 39(2):292-298(施蓓琦, 刘春, 陈能, 等. 典型地物实测光谱的相似性测度与实验分析[J]. 同济大学学报(自然科学版),2011, 39(2):292-298) |
| [16] | Mémoli F. Some Properties of Gromov-Hausdorff Distances[J]. Discrete & Computational Geometry, 2012, 48(2):416-440 |
| [17] | Helmut A, Michel G. Computing the Fréchet Distance Between Two Polygonal Curves[J].International Journal of Computational Geometry & Applications,1993, 5(1/2):75-91 |
| [18] | Buchin K, Buchin M, Wenk C. Computing the Fréchet Distance Between Simple Polygons[J].Computational Geometry,2008, 41(1/2):2-20 |
| [19] | Pelletier S. Computing the Fréchet Distance Between Two Polygonal Curves: Computational Geometry[OL]. http://www.cim.mcgill.ca/-stephane/cs507/Project.html,2014 |
 2016, Vol. 41
2016, Vol. 41