文章信息
- 杨景辉, 张继贤
- YANG Jinghui, ZHANG Jixian
- 结合多种分解策略的遥感影像去相关拉伸并行处理方法
- The Parallel Decorrelation Stretching with Multiple Decomposition Tactics for Remotely Sensed Imagery
- 武汉大学学报·信息科学版, 2016, 41(3): 402-407
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 402-407
- http://dx.doi.org/10.13203/j.whugis20140222
-
文章历史
- 收稿日期: 2014-12-13

2. 中国测绘科学研究院, 北京, 100830
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China
去相关拉伸能增强色彩饱和度[1, 2],减少波段间的相关性,广泛应用于专题信息制图、影像分类和解译判读等。去相关拉伸技术一般先经过一个主成分变换(principal component transformation,PCT)之后,将变换后的变量进行对比度拉伸,然后再通过主成分反变换转换成原数据空间[2]。因此,需要统计影像波段信息、计算影像波段间的协方差矩阵及进行线性变换,处理过程相对复杂,具有一定的计算复杂度。目前,鲜有去相关拉伸的并行处理的研究,与之相近的研究工作包括:Achalakul等针对HYDICE高光谱影像提出了光谱筛查的主成分变换并行处理技术[3],并在分布式集群计算机下进行测试,相关工作没有扩展至影像去相关拉伸算法;王茂芝等在集群计算环境下实现了高光谱遥感数据主成分变换中的协方差矩阵求解的并行处理[4],没有实现主成分变换算法全部过程的并行化。
相关的研究工作为基于集群、多核CPU和GPU的并行处理算法,这些算法多集中在几何校正和高光谱影像处理。如使用集群计算机进行高光谱影像信息提取并行处理[5, 6];多核平台下使用OpenMP等库实现高光谱端元提取[7]和混合像元分解[8],采用的核数不多(最多12核),且没有经过并行策略优化,扩展性不高,只取得了约3倍的加速;使用GPU进行几何校正[9]、雷达立体测量[10]、ZY-3遥感影像预处理[11]。
本文所指的多核计算机是包括单个或多个CPU,具有多个计算核心的计算机系统,此种计算机价格低,容易管理与使用,已经具有较强的计算能力应对遥感影像处理。
1 遥感影像去相关拉伸并行处理方法 1.1 去相关拉伸处理步骤传统去相关拉伸技术的实现步骤[2]如下。
1) 统计波段信息,计算影像波段间协方差矩阵,特征值特征向量求解等;
2) 通过PCT变换将影像变换至主成分变量;
3) 主成分变量进行拉伸,一种可能是均衡化主成分变量;
4) 主成分变量进行PCT逆变换,得到去相关拉伸后结果。
上述去相关拉伸技术可通过3个连续的矩阵变换实现,且使用了PCT正反变换。因为去相关拉伸是基于像素矢量(像素矢量包括多个波段对应的像素值)的矩阵变换,上述步骤2)~步骤4)对应的变换矩阵相乘,即可得到最终变换矩阵。Campbell研究发现,去相关拉伸可通过一个替代的线性变换实现[12],该线性变换即为上述最终变换矩阵,其变换结果与采用PCT正反变换相同。因此,为实现去相关拉伸主要任务是确定线性变换矩阵。
根据文献[12],最终线性变换矩阵可通过3个矩阵相乘得到,去相关拉伸结果通过式(1)计算:

式中,Xm=(X1m,…,Xvm)和Zm=(Z1m,…,Zvm)分别表示去相关拉伸前、后影像的第m个像素矢量,每个矢量包括v个波段对应的像素值;UT为PCT正变换系数矩阵;U为PCT逆变换系数矩阵;E=diag(e1,…,ev),e1,…,ev为步骤1)中协方差矩阵求解的v个特征值;UE-1/2UT为最终变换矩阵。为计算U、E等变换矩阵,需要用到影像各波段的统计信息,计算波段之间的协方差矩阵等。
Campbell[12]提出的去相关拉伸实现技术是一种高效的方法,上述步骤2)~步骤4)(PCT正变换、均衡化和PCT逆变换)压缩成一步,只需进行一次线性变换,但两种方法都需要计算影像波段统计信息和波段之间的协方差矩阵等。本文采用Campbell提出的去相关拉伸技术,根据各步骤的特点提出不同的并行分解策略,实现了全过程的并行处理。
1.2 本文去相关拉伸并行处理方法采用消息传递库(message passing interface,MPI)为并行运行环境,多核计算平台下,一个计算核心(或通过超线程得到的虚拟核心)对应于MPI并行环境中一个进程。将进程分成主进程和从进程两类,主进程由0号进程担当,其他进程为从进程。整个并行处理流程如图 1。

|
| 图 1 结合多种分解策略的去相关拉伸并行处理方法 Fig. 1 Parallel Decorrelation Stretching with Multiple Decomposition Tactics |
首先,从进程按波段进行波段信息统计,波段均匀分配给各从进程。某一时刻一个从进程对应一个波段,读取波段数据并进行统计,一个波段完成之后紧接着处理其对应的下一个波段;如果波段数小于从进程的个数,任务分配给进程编号小的从进程,部分进程空闲。统计信息包括本波段的最大值、最小值、均值和标准差等。各从进程将统计的波段信息发送给主进程,主进程接收后,将所有波段统计信息进行广播,自此所有进程都具有了全部波段的统计信息。
各从进程按波段对方式进行协方差矩阵元素的计算。因为协方差矩阵为对称阵,且为方阵,对角线元素为同一波段的方差,因此,需要计算的矩阵元素为剔除对角线的上三角矩阵包括的元素。计算协方差矩阵元素时需要用到两个波段,两个波段形成一个波段对,多个波段对均匀地分配给各从进程,从进程读取波段数据并进行计算,将计算的协方差矩阵元素发至主进程。主进程接收后,求解协方差矩阵的特征值和特征向量,计算3个矩阵相乘的最终线性变换矩阵,并将变换矩阵进行广播,自此所有进程都具有最终线性变换矩阵。
最后,各从进程按数据块进行线性变换,多个数据块均匀地分配给各从进程,实验采用的数据块大小为64像素×64像素。从进程读取对应的数据块并进行矩阵变换,将变换结果发送至主进程,主进程将接受的数据块写入结果影像。
图 1中不同步骤采用不同任务分解策略,本文编写了实现图 1流程的C++程序,并在两台多核计算机下进行了并行处理实验。
2 实验结果 2.1 实验平台及影像两台多核工作站用于实验。一台为安装Windows 7操作系统的Dell Precision T7500 工作站(简称Windows计算机),单个6核Intel Xeon X5675 CPU (3.06 GHz),通过超线程技术虚拟成12核,48 GB内存,120 GB固态硬盘,NTFS文件系统,编译器和MPI库分别为Visual Studio C++ 2010和Intel MPI 4.0;另一台为安装Linux操作系统的定制性工作站(简称Linux计算机),两个4核Intel Xeon E5520 CPU (2.26 GHz),通过超线程技术虚拟成16核,12 GB内存,6个SAS磁盘构建RAID 0,ext3文件系统,编译器和MPI库分别为GNU GCC 4.1.2 和LAM-MPI 7.1.1。
实验使用两组影像:一组为国产OMIS高光谱遥感影像,504 MB,影像尺寸为512像素×4 000像素,数据类型为有符号16位整型,128个波段;另一组为ASTER卫星影像,181 MB,影像尺寸为4 980像素×4 200像素,数据类型为无符号8位整型,可见光和近红外(VNIR)3个波段和短波红外(SWIR)6个波段共9个波段,由于VNIR分辨率为15 m,SWIR分辨率为30 m,需将SWIR采样至15 m。所有影像均采用ERDAS IMAGINE格式进行存储。
2.2 实验结果去相关拉伸前后OMIS影像如图 2,用于显示波段组合1、4、7;去相关拉伸前后ASTER卫星影像如图 3,用于显示波段组合5、6、7。对比图 2(a)和图 2(b),去相关拉伸后影像较清晰,各种特征反映较明显,尤其是图 2(a)四周亮度过高的区域经过去相关拉伸处理后亮度适中且整个影像变化平缓;对比图 3(a)和图 3(b),原始影像波段组合5、6、7显示时地物彩色信息少,类似于灰度影像,去相关拉伸后不同地物呈现不同的色彩,区别特征明显,更加便于判读解译。经过计算,图 2(b)和图 3(b)各自用于显示的波段之间的相关系数均小于拉伸前。
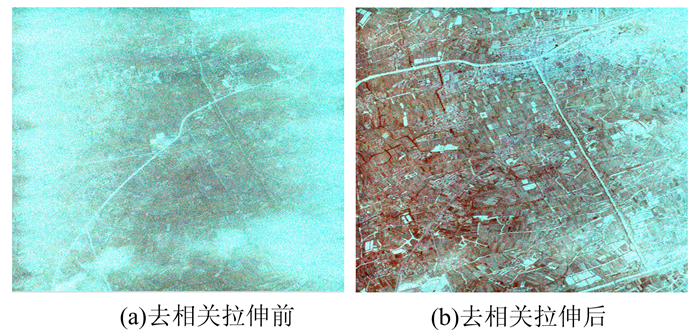
|
| 图 2 OMIS高光谱遥感影像去相关拉伸前后显示 Fig. 2 OMIS Images Before and After Decorrelation Stretching |

|
| 图 3 ASTER卫星影像去相关拉伸前后显示 Fig. 3 ASTER Images Before and After Decorrelation Stretching |
实验分别记录了串行处理和多核并行处理所用时间,串行处理只利用单个处理核心,也即图 1中的所有步骤全部由一个CPU核心完成。记录的时间是完成影像去相关拉伸的整个流程的全部时间,包括程序初始化时间、影像读写时间和计算时间。为检验并行性能,加速比作为评价指标用于后面的实验和分析,加速比定义为:

式中,ts是串行处理时间;tp是多核并行处理时间。
表 1和表 2分别给出了Windows计算机下和Linux计算机下不同进程执行时间及相应的加速比。表 1中Windows计算机下实验结果显示,单进程串行处理ASTER影像只需22 s,而在相同计算平台下商业软件ERDAS IMINGE需要43 s,说明本文采用的去相关拉伸技术处理效率更高。在使用两个进程并行处理时,其时间与串行处理基本一致,这是因为两个进程情况下只有一个进程用于计算;随着CPU核数的增加,执行时间逐渐减少;当使用全部12进程并行处理时,时间最少,相应的加速比也达到了最大,如表 1中黑体显示。表 2中Linux计算机下实验结果规律与表 1基本一致,当使用全部16进程并行处理时,时间最少,加速比也达到了最大,如表 2中黑体显示。
| 实验数据 | 进程数 | |||||||
| 1 | 2 | 4 | 6 | 8 | 10 | 12 | ||
| OMIS | 时间/s | 277 | 328 | 118 | 75 | 56 | 46 | 42 |
| 加速比 | 1.0 | 0.8 | 2.3 | 3.7 | 4.9 | 6.0 | 6.6 | |
| ASTER | 时间/s | 22 | 21 | 11 | 8 | 8 | 6 | 6 |
| 加速比 | 1.0 | 1.0 | 2.0 | 2.8 | 2.8 | 3.7 | 3.7 | |
| 实验数据 | 进程数 | |||||||||
| 1 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | ||
| OMIS | 时间/s | 964 | 882 | 304 | 189 | 197 | 185 | 152 | 137 | 122 |
| 加速比 | 1.0 | 1.1 | 3.2 | 5.1 | 4.9 | 5.2 | 6.3 | 7.0 | 7.9 | |
| ASTER | 时间/s | 55 | 47 | 17 | 17 | 13 | 11 | 9 | 9 | 8 |
| 加速比 | 1.0 | 1.2 | 3.2 | 3.2 | 4.2 | 5.0 | 6.1 | 6.1 | 6.9 | |
表 1中,Windows计算机下进行OMIS影像处理时,使用2个进程的执行时间比单进程执行时间长。记录了处理OMIS影像的3部分时间(波段信息统计、协方差矩阵求解和线性变换),发现使用两个进程进行协方差矩阵求解时所用时间大于单进程所用时间,单进程时间为120.17 s(总时间为280 s),而两个进程时间为175.44 s(总时间为328 s);而其他两部分时间基本一致。原因是使用两个进程进行协方差矩阵求解时,实际只有一个从进程进行运算,主进程只负责接收处理结果,从进程需向主进程发送8 128个求解的协方差矩阵元素(协方差矩阵为对称阵,且为方阵,剔除对角线的上三角矩阵元素个数为(128×128-128)/2=8 128,由于波段多而导致大的协方差矩阵需要更多的通信,因此,两个进程处理时间反而比单进程时间长。
比较OMIS和ASTER两组影像实验结果,进程数大于等于4时OMIS影像取得的加速比高于ASTER影像,原因是两种影像具有不同的波段数而造成不同规模计算量,波段数越多所需计算量越大,OMIS影像进行去相关拉伸时,为计算一个波段中一个像点值,要计算128元一次多项式,而ASTER影像只需计算9元一次多项式。所需计算量越大,更多进程参与计算时,并行效率更高,扩展性更高;计算量太小而不足于让各进程忙碌起来,进而并行效率低。因此,单位影像尺寸所需计算规模是决定并行处理性能的一个重要因素,所需计算量越小其并行处理性能越低,所需计算量越大其并行处理性能越高。另外,去相关拉伸并行处理过程中需要进行多次文件读写操作,且磁盘处理能力相对于其他计算机部件性能更低,因此,为了提高整体性能,在应用过程中应该尽量选用高性能磁盘,优化遥感影像文件组织及读写性能,将CPU计算能力和磁盘读写能力进行匹配,避免磁盘性能低下造成的瓶颈。
去相关拉伸中线性变换采用按数据块划分的并行处理方法,表 1和表 2为块大小设置为64像素×64像素的实验结果,为分析块大小对处理性能的影响,比较了多种块大小的实验结果。表 3和表 4分别为OMIS影像在两个计算平台下不同块大小配置下执行时间,表中黑体表示本文采用的块大小的实验结果。表 3显示,64像素×64像素相比其他块大小具有更好的性能;表 4中,32像素×32像素和64像素×64像素两种块配置具有较好的性能。根据两个平台的实验结果,64像素×64像素是一个较优的选择,而该块长也和采用的影像文件格式ERDAS IMAGINE的文件块大小一致。
| 块大小 | 进程数 | ||||||
| 1 | 2 | 4 | 6 | 8 | 10 | 12 | |
| 32×32 | 282 | 326 | 121 | 80 | 60 | 50 | 45 |
| 64×64 | 277 | 328 | 118 | 75 | 56 | 46 | 42 |
| 128×128 | 391 | 417 | 155 | 96 | 72 | 59 | 52 |
| 256×256 | 434 | 478 | 173 | 109 | 85 | 70 | 59 |
| 512×512 | 793 | 843 | 339 | 230 | 160 | 128 | 125 |
| 块大小 | 进程数 | ||||||||
| 1 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | |
| 32×32 | 964 | 876 | 295 | 311 | 200 | 181 | 145 | 133 | 111 |
| 64×64 | 964 | 882 | 304 | 189 | 197 | 185 | 152 | 137 | 122 |
| 128×128 | 1 072 | 970 | 331 | 300 | 235 | 193 | 162 | 143 | 132 |
| 256×256 | 1 134 | 1 055 | 357 | 220 | 259 | 199 | 174 | 150 | 138 |
| 512×512 | 1 228 | 1 079 | 432 | 302 | 274 | 291 | 250 | 262 | 238 |
本文提出了一种结合多种分解策略的遥感影像去相关拉伸并行处理方法,并在两台多核计算机下进行了测试,结果显示通过合理配置CPU核数和磁盘系统等,目前常用的12~16核计算机可取得约4~8倍的整体加速比。单位影像尺寸所需计算规模和影像读写能力是决定去相关拉伸并行处理整体性能的重要因素。去相关拉伸影像波段数越多,其计算规模越大,具有更好的并行效率和扩展性,可选用更多的CPU核参与运算;尽量选用高性能磁盘,优化遥感影像读写性能,将CPU性能和磁盘性能进行匹配,避免磁盘性能低下造成的瓶颈。本文方法在遥感影像应急快速处理、地面接收站批量处理等数据量大或时间响应短的应用方面具有较大优势。
本文方法可直接用于PCT变换、基于PCT的影像融合及基于PCT的变化检测等算法。由于采用的分解策略充分顾及各种遥感影像处理算法特点,对不同算法和遥感数据源都具有一定的适用性。未来选用CPU核数更多(如32核以上)和磁盘性能更强的平台进行测试,可进一步优化扩展性。
| [1] | Soha J M, Schwartz A A. Multispectral Histogram Normalization Contrast Enhancement [C]. The 5th Canadian Symposium on Remote Sensing, Victoria, BC, Canada, 1978 |
| [2] | Gillespie A R. Enhancement of Multispectral Thermal Infrared Images: Decorrelation Contrast Stretching [J]. Remote Sensing of Environment, 1992, 42(2): 147-155 |
| [3] | Achalakul T, Taylor S. A Distributed Spectral-screening PCT Algorithm [J]. Journal of Parallel and Distributed Computing, 2003, 63(3): 373-384 |
| [4] | Wang Maozhi, Guo Ke, Xu Wenxi. Hyperspectral Remote Sensing Image Parallel Processing Based on Cluster and GPU[J]. Infrared and Laser Engineering, 2013, 42(11): 3 070-3 075 (王茂芝,郭科,徐文皙. 基于集群和GPU 的高光谱遥感影像并行处理[J]. 红外与激光工程, 2013, 42(11): 3 070-3 075) |
| [5] | Plaza A, Valencia D, Plaza J, et al. Commodity Cluster-based Parallel Processing of HyperspectralImagery [J]. Journal of Parallel and Distributed Computing, 2006, 66(3): 345-358 |
| [6] | Luo Wenfei, Zhang Bing, Jia Xiuping. New Improvements in Parallel Implementation of N-FINDR Algorithm [J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(10): 3 648-3 659 |
| [7] | Remon A, Sanchez S, Paz A, et al. Real-time Endmember Extraction on Multi-core Processors [J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(5): 924-928 |
| [8] | Bernabe S, Sanchez S, Plaza A, et al. Hyperspectral Unmixing on GPUs and Multi-Core Processors: A Comparison [J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2013, 6(3): 1 386-1 398 |
| [9] | Yang Jingyu, Zhang Yongsheng,Li Zhengguo,et al. GPU-CPU Cooperate Processing of RS Image Ortho-Rectification[J]. Geomatics and Information Science of Wuhan University, 2011, 36(9): 1 043-1 046 (杨靖宇,张永生,李正国,等. 遥感影像正射纠正的GPU-CPU协同处理研究[J]. 武汉大学学报·信息科学版, 2011, 36(9): 1 043-1 046 ) |
| [10] | Balz T, Zhang L, Liao M. Direct Stereo Radargrammetric Processing Using Massively Parallel Processing [J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2013, 79(1): 137-146 |
| [11] | Fang L, Wang M, Li D, et al. CPU/GPU Near Real-time Preprocessing for ZY-3 Satellite Images: Relative Radiometric Correction, MTF Compensation, and Geocorrection [J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2014, 87(1): 229-240 |
| [12] | Campbell N A. The Decorrelation Stretch Transformation [J]. International Journal of Remote Sensing, 1996, 17(10): 1 939-1 949 |
 2016, Vol. 41
2016, Vol. 41


