文章信息
- 郭越, 王晓峰, 张恒振
- GUO Yue, WANG Xiaofeng, ZHANG Hengzhen
- 基于人类感知的SAR图像海上溢油检测算法
- Oil Spill Detection by SAR Images Based on Human Perception
- 武汉大学学报·信息科学版, 2016, 41(3): 395-401,407
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 395-401,407
- http://dx.doi.org/10.13203/j.whugis20140404
-
文章历史
- 收稿日期: 2014-10-07

当SAR图像上出现了与油膜类似的成像特征时,如何对海面特征进行检测需要解决两方面问题。一方面需要从SAR图像中抽取可以表征油膜特点的特征;另一方面需要快速、精准的分类算法对抽取出的特征进行识别。传统的海上SAR溢油监测研究中,主要以待识别物质的灰度信息为依据。但如果识别物质具有相似的后向散射性质,那么在SAR图像中也会表征出相似或相同的灰度值,从而无法区分出“类油膜”特征,使辨别发生混淆。因此仅通过灰度值进行分类在实际识别应用中效果不佳。而纹理特征取决于空间色调的相对变化,不仅可以有效地进行边缘检测,还能够提高SAR图像中同一级别灰度区域的分类精度,所以不同目标物的纹理会在外观上存在较大的差异。这已成为SAR图像识别分类应用中的重要特征[1]。Topouzelis等人提取了5个几何特征运用RBF神经网络的方法对海上SAR遥感图像进行识别[2]。赵大康通过对ERS-2 泰国湾SAR溢油影像的灰度和纹理特征信息的提取,利用人工神经网络进行分类[3]。石立坚通过方差分析方法对ERS-2 SAR溢油图像的纹理特征进行分析和筛选,利用BP神经网络方法识别油膜与类油膜[4]。Mansor等建立了包括:孔径模式校正、辐射校正、几何校正、暗油层探测、纹理分析、特征提取、Gamma滤波、油层分类等环节的SAR溢油探测技术流程和分类算法[5]。何楚等提出了利用特征选择自适应决策树的层次SAR图像分类方法[6]。巫兆聪等应用分水岭变换与支持向量机对极化SAR图像分类[7]。
以往的研究中,大部分算法需要对SAR原始图像进行繁琐的预处理操作。在实际应用中,单一的预处理对来源不同的雷达影像是不适用的。为了提高海上溢油SAR图像的应用可行性,本文运用Tamura特征与灰度共生矩阵这两种纹理特征,直接对原始SAR图像中油膜、类油膜和海水的特征进行提取。在实际应用中,人类专家能够在较短的时间内对SAR图像中的单一溢油区域进行较准确的判定。深度学习的方法恰好能够较好的模仿人脑在“深度”模式下认识抽象概念的方式。但由于深度学习的算法比较复杂,确定其运算参数是个难点。本文通过实验确定了深度信念网中隐含层信息处理元个数、训练次数、学习率、训练样本与测试样本的最佳比例,以及扰动量等关键参数。应用选定参数的深度信念网对纹理特征进行分类,识别准确率达到90.36%。
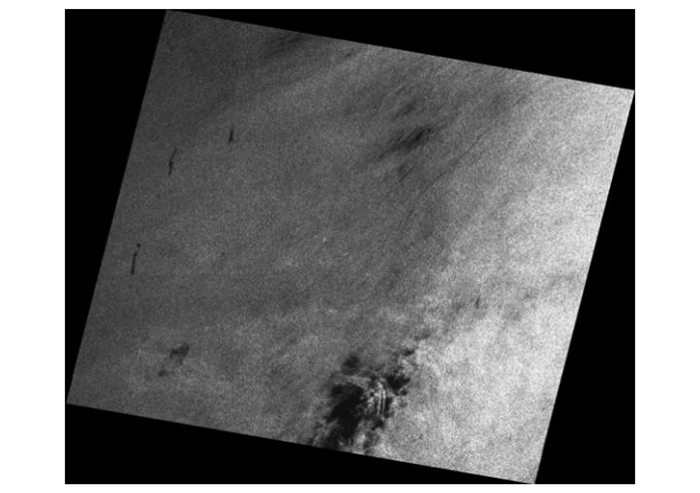
1 数据集本文数据来源于30景海上溢油SAR图像,溢油区域位于中国南海,所有数据已经给出了对溢油点定性及定量的评价,本次试验溢油样本所在区域如图 1所示。每景溢油图像分辨率为100 m,文件格式为GeoTIF,如图 2所示。SAR遥感图像来源于ers-1和ers-2两颗卫星,图像带有卫星拍摄时的详细信息(卫星:Envisat,传感器:ASAR,时间:2004-03-02: 02:25:43,溢油数量:9,纬度:19.519 882°,经度:113.851 955°,风力:6~9节)。由于星载SAR图像具有高分辨率、大覆盖面成像的特点,即使是大面积的海上溢油,在SAR图像中的溢油区域相对于海面背景来说依旧较小。所以需要对SAR图像按照油膜、类油膜、海水三种类别进行适当合理的切割,所得图像大小为120像素×120像素(图 3)。油膜、类油膜及海水样本各为400个,共计1 200个样本。图像数据样本为随机存储,同时对1 200个样本进行相应的打乱操作,以保证随机分配训练样本和测试样本。

|
| 图 1 实验数据原始溢油图像区域(位于中国南海) Fig. 1 Region of Original Spill Image in Our Experiment(Located in the South China Sea) |
|
| 图 2 SAR溢油原始图像 Fig. 2 Original SAR Image With Oil Spill |

|
| 图 3 120×120样本图像 Fig. 3 120×120 Sample Image |
本文首先对原始图像进行切割,得到油膜、类油膜及海水这三类样本图像。计算三类样本图像的Tamura特征以及灰度共生矩阵特征,将得到的特征组成特征空间矩阵。然后应用DBN对该特征矩阵进行学习分类,测试不同DBN参数对分类效果的影响,确定最适合本次分类的参数。最后,应用DBN方法对样本特征进行分类,并与现有方法进行比较。
2.1 Tamura特征Tamura特征是根据纹理的视觉感知心理学得出的。该特征给出了6个与人的视觉感受密切相关的纹理特征:粗糙度、对比度、方向性、线像度、规整度和粗略度[8]。这些纹理特征很好地反映了人类视觉感知,尤其适用于灰度图像的特征提取。本文选取了粗糙度、对比度、方向性与线像度这4个特征,并计算线像度在8个方向上的均值及方差,得到共计6个Tamura特征值。
2.2 灰度共生矩阵特征提取灰度共生矩阵(gray level co-occurrence matrix,GLCM)是一种基于结构的纹理特征。该方法主要通过两个步骤来完成:① 描述纹理基元的性质;② 描述纹理基元的组织方式。纹理基元是一组由属性所规定的连通的像素集合,主要包括方向、平均灰度、尺寸等属性。一幅图像的GLCM能反映出该图像的灰度级关于方向、相邻间隔、变化幅度上的综合信息,是分析图像内在局部信息和外在序列规则的基础。对于粗纹理的区域,GLCM的值趋于两极分化,较集中于主对角线附近;对于细纹理的区域,则分布较散,因而需要更深一步对其纹理分布进行描述。本文从GLCM中计算出了14个特征统计量来进一步描述纹理分布。从中选取了常用的角二阶矩、对比度、相关性、熵和逆差距等5个特征。对于每一类特征分别计算其在0°、45°、90°、135°等4个方向上的特征信息,得到20维特值。然后分别计算5个特征在4个方向上的均值和方差,得到10维特征值。因此,灰度共生矩阵共计得到30维特征值(式(1))。
2.3 深度信念网络(DBN)人脑具有深度结构的特点,ANN研究者们也一直致力于多层深度的神经网络研究[9, 10]。但训练一个有一定深度的网络有一定难度,原因在于当多层网络从随机的权值参数开始训练时,很容易陷入局部最优解。Hinton等提出的深度信念网络(DBN)则应用了一种无监督的预训练方法,成功解决了这个问题[11]。由限制波兹曼机(RBM)基本模块搭建而成的DBN是一个多层结构的生成式网络模型。通过自下而上的层级训练方式,将模型参数限定在了对下一步学习有利的数值范围内。这种无监督预训练与监督训练学习微调的思想在机器学习领域产生了巨大的影响。
Bengio用实验证明了深度学习可通过学习一种深层非线性网络结构,实现复杂函数逼近,表征输入数据分布式表示,并展现了强大的从少数样本集中学习数据集本质特征的能力[12, 13]。因此,深度学习能够解决溢油检测中小样本分类的问题。文献[15]也对SVM及深度学习的运算效率及准确率进行了对比,结果表明深度学习明显优于SVM等其他算法。目前,最有效的溢油识别方法仍然是人的经验,而深度学习方法能够模仿人脑高效、准确地表示信息的方式。本文试图将人类感知与认识事物的方式应用于溢油识别中,因此,选取DBN对由Tamura和GLCM抽取出来的纹理特征进行分类。
2.4 Tamura与GLCM的特征组合本文采用特征组合的方法,从原始图像中选取特征进行组合,形成特征矢量。不同特征组合后的特征可以更好地检测目标。采用Tamura与GLCM提取的特征构成表征溢油信息的特征矢量。
Tamura和GLCM特征都是基于图像灰度矩阵的特征提取方式。它们各自的提取过程在本质上可以说是并列的,所以本文将结合两种特征,对图像提取Tamura的粗糙度、对比度、方向性、线像度以及8个方向的线像度均值和方差共计6个特征值。提取GLCM中的能量、熵、相异性、逆差距和自相关性,以及这些特征各自的均值和方差共计30个特征。共组成36维特征向量供分类使用。组合后的特征描述如式(1)所示:

式中,X1-30为GLCM的纹理特征;X31-36为Tamura的纹理特征。
3 实验与结果分析 3.1 特征数据预处理特征值中每个维度代表不同的特征,而不同特征的取值范围不同,这使得特征向量的各特征分量会在数量级上存在较大的差别性。由代价函数可知,较大的特征分量的影响效果要大于较小的特征分量,但这并不意味着大特征分量对识别效果更重要,因此,需要对特征值进行数量级的统一,即特征归一化操作[14]。
图像训练样本集为{train_xi},测试样本集为{test_xi},计算训练样本集所有样本的平均值train_x,则归一化后的训练特征值为train_xi*:
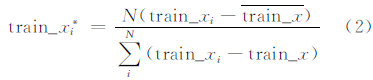
式中,N为训练的样本数量,经归一化后操作后,训练样本集下的各样本分量值均在[-1,+1]范围内。测试样本使用同样的归一化方法。
3.2 DBN参数选取DBN网络精度的提高可以通过增加隐含层层数或隐含层信息处理元的个数来实现。但网络层数增加的同时,也增加了网络的复杂性。而增加信息处理元个数要比增加层数简便得多。溢油检测属于小样本分类,文献[15]提出隐含层的层数及每层的计算单元数与数据集的大小成正比。由于溢油识别属于小样本检测,为了分析DBN中层数及隐藏单元个数对算法的影响,我们分别对3种不同隐含层进行分析,比较其对于准确率的影响。实验单元个数为80,80-50,80-50-20。训练次数为100次,学习率为0,动量为1。
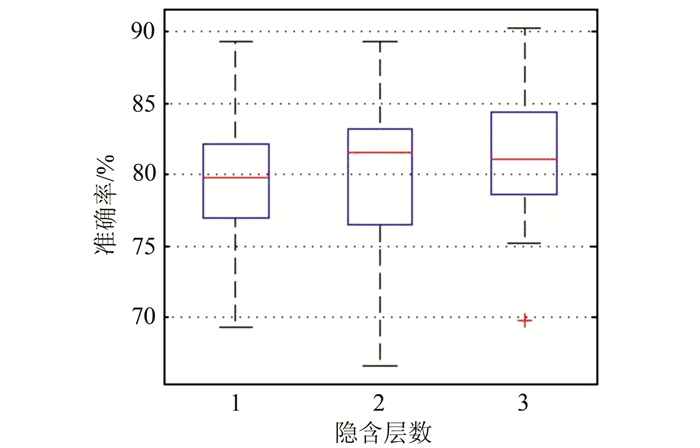
从图 4中可以看出,当隐含层为1时准确率较低,均值小于80%。当隐含层数为2时,准确率明显提高,但是四分区间比较大,下边缘也比较低。这说明准确率虽然部分提高,但分类的准确度不是很稳定。当隐含层数为3时,出现了最高准确率,虽然均值率略低于2层,但大部分分类准确率在80%以上。为了确定隐含层的树目,我们分别在3个隐含层中取不同节点数目的分类准确率及训练所需时间进行比较,如图 5所示。
|
| 图 4 不同数目隐含层对准确率的影响 Fig. 4 Effects of Hide Layers on Classification Accuracy |
|
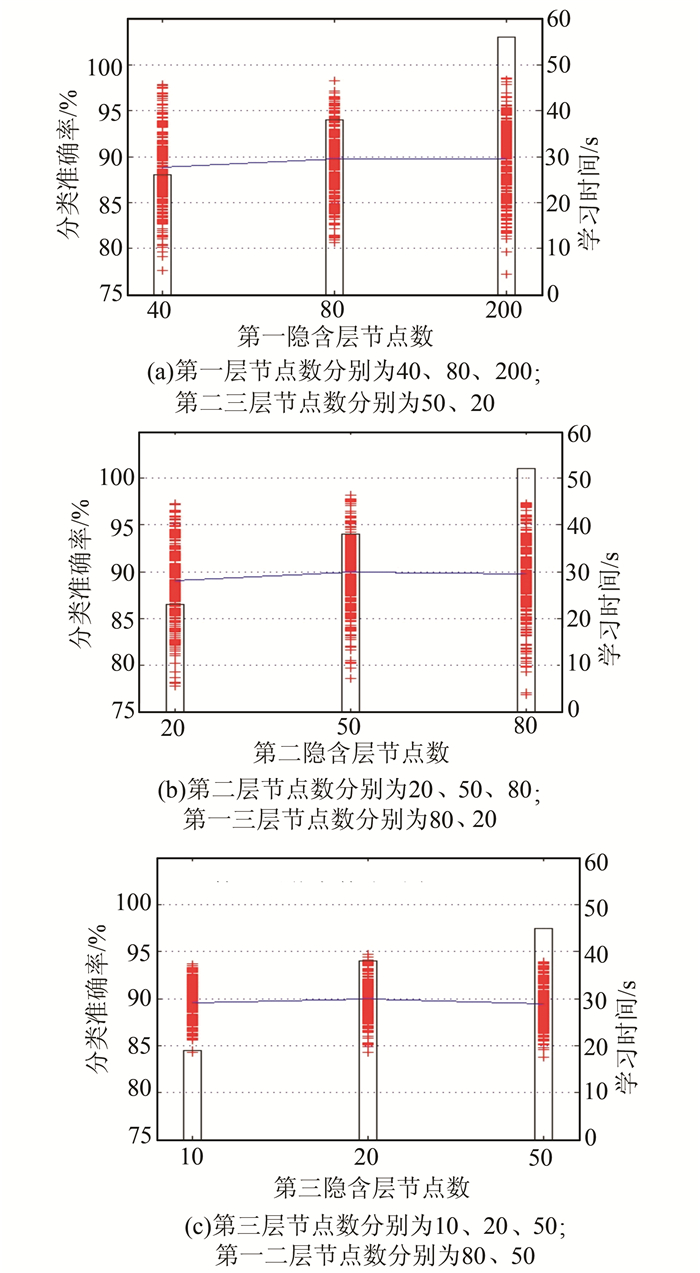
| 图 5 不同隐含层节点数目对分类准确率的影响 Fig. 5 Different Effects of Hidden Neurons Number on the Accuracy of Classification |
从图 5(a)中可以看出,第一层节点个数为80与200时分类准确率的均值相当,但明显高于结点个数为40的结构,且节点个数为80的学习时间明显低于200。图 5(b)与图 4(a)的情况基本类似。图 5(c)说明当第三层选择10或者50个节点时,分类准确率的均值都会略低与20,且学习时间也与节点个数成正相关。
综合考虑分类准确率及学习时间,本文选用3层结构,即3组RBM基本模块单元,将隐层信息处理元个数设置为80-50-20。
由于DBN算法参数较多,因此确定DBN的关键参数也是本文研究的一部分。DBN的训练次数直接关系到算法的学习效果和分类能力。训练次数太少,DBN模型学习不够充分,学习效果不好,更谈不上分类能力;训练次数太多,DBN有可能把训练样本的个性记住,忽略了共性特征。这会造成模型的学习集误差很低,预测集误差却很高,因而模型的预测能力下降。为了确定不同训练次数与不同样本数量对DBN的影响,本文分别选取了9种训练次数,10%~80%的样本做为训练数据进行比较。为了方便描述,将Tamura与GLCM的特征组合简称为TUGLCM。从图 6中可以看出,对于相同的训练次数,不同训练样本比例所得到的准确率有很大差别。但是,对于不同数量的训练样本,训练次数为200时准确率都达到最高。说明DBN确实存在过度训练的问题,且DBN对于TUGLCM特征在训练200次时具有较好的收敛性能。
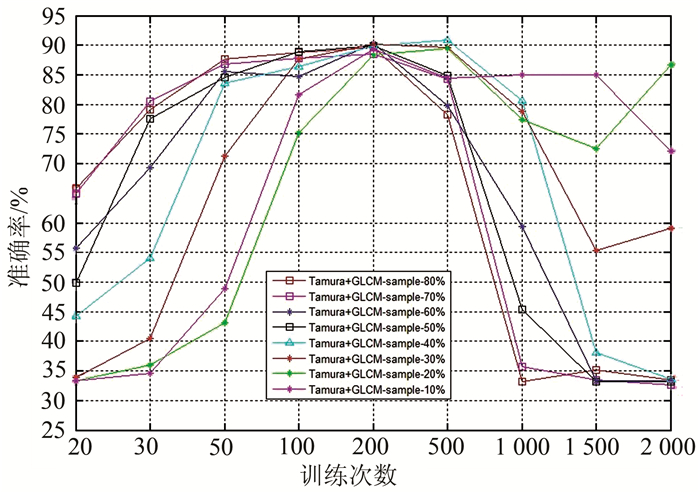
|
| 图 6 不同训练次数对分类准确率的影响 Fig. 6 Effect of Different Training Times on the Accuracy of Classification |
RBM中学习速率(learning rate,lr)参数的调整决定了每次训练过程中产生权值的变化量。较高的lr值会影响系统的稳定性;较低的lr值会造成收敛效果缓慢,但能保证网络误差值跳出局部极小值并最终达到全局最优值解。通常情况下,DBN算法都倾向于选择较小的lr,每一个具体的网络模型都会有一个最适合它的lr。本文验证了0~1共10种不同的lr对于不同训练样本比例的准确率。从图 7可以看出,当lr取0时,不同比例的训练样本的分类准确率最高,而当lr较大时,准确率都较低。因此,本文选取lr值为0。
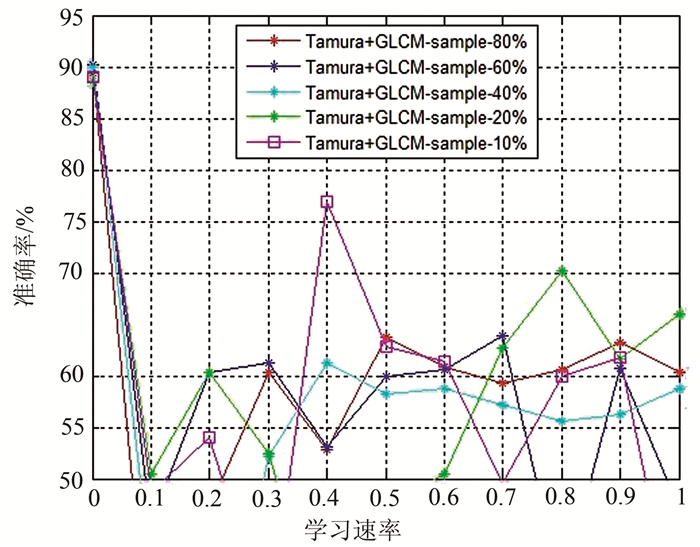
|
| 图 7 不同学习速率对分类准确率的影响 Fig. 7 Effects of Different Learning Rate on the Accuracy of Classification |
在经典的反向传播算法中,lr值越小就意味着从一次迭代到下一次迭代的网络权值的变化量越小,即好的收敛性是以减缓学习速度为代价的。因此,Rumelhart等[16]提出增加一个动量参数m以确保加快学习速度的同时也能保持网络的稳定。本文通过对不同样本数量(不同比例的学习及测试样本)的准确率进行测试,发现动量m对分类效果的影响较小,且变化趋势较为平稳,因此,m可设置为0.9或1,本文实验中则设为0.9。如图 8所示。
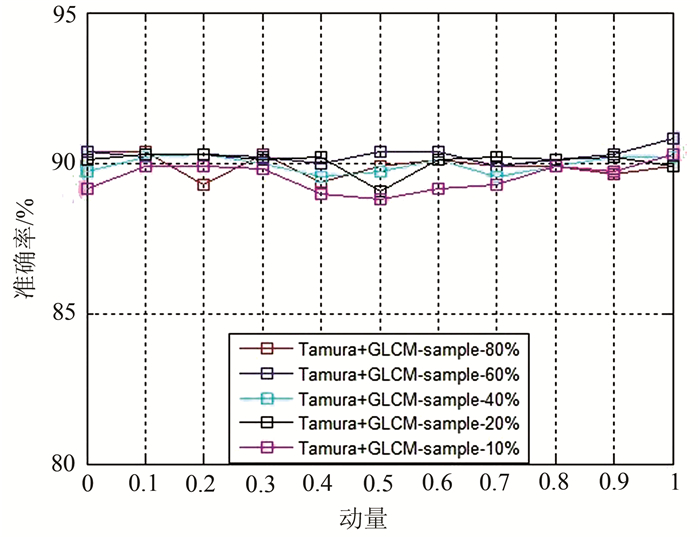
|
| 图 8 不同动量值对分类准确率的影响 Fig. 8 Effects of Momentum on the Accuracy of Classification |
为了确定训练样本与测试样本的最佳比例,对不同比例的训练样本进行测试。本文选取10%~80%的8种训练样本(训练次数为200次)对DBN的分类准确率进行了比较,结果表明,当训练样本个数占30%时,分类准确率均值最高为90.28%。因此,油膜、类油膜及海水中,训练样本的个数均取120个,测试样本的个数皆为280个。在所有1 200个样本中,训练样本为120×3=360个,测试样本为280×3=840个。
3.3 实验过程与结果分析为了对比在相同特征空间,不同训练次数下DBN与神经网络(NN)的分类准确率,选取了30%的训练特征在不同训练次数下的分类准确率进行比较(表 1)。
| 训练次数 | 30 | 50 | 100 | 200 | 500 | 1 000 | 1 500 | 2 000 |
| DBN/% | 40.48 | 71.30 | 87.67 | 90.36 | 89.62 | 78.91 | ||
| NN/% | 85.88 | 87.11 | 74.81 | 87.00 | 80.18 | 87.38 | 72.12 | 66.46 |
由表 1可以看出,使用DBN进行分类,在训练次数为200次时分类准确率最高,为90.36%;而使用NN进行分类,需要训练1 000次才能达到最佳分类准确率87.38%。所以,NN的分类准确率不但比DBN低,而且效率也低于DBN。
为了更深入分析本文算法对海水,油膜以及类油膜的分类效果。我们使用30%的样本特征进行学习,油膜、类油膜及海水的测试数量分别为280个。经过200次训练后对比DBN与NN对相同TUGLCM特征的分类效果,见表 2。
| 方法 | 油膜 | 类油膜 | 海水 | 类别精度/% | ||||
| NN | DBN | NN | DBN | NN | DBN | NN | DBN | |
| 油膜 | 267 | 267 | 11 | 13 | 2 | 0 | 95.36 | 95.36 |
| 类油膜 | 15 | 19 | 225 | 235 | 40 | 26 | 80.36 | 83.93 |
| 海水 | 0 | 0 | 38 | 23 | 242 | 257 | 86.43 | 91.79 |
| 总精度/% | 87.38 | 90.36 | ||||||
从表 2可以看出,两种分类方法对油膜的识别效率是一样的。而对于类油膜与海水来说,DBN的识别率要明显高于NN。在未正确分类的13个油膜样本中,DBN全部识别为类油膜,而NN则将11个分为类油膜,2个分为海水。这说明运用DBN算法,识别海水与油膜不会发生混淆,而基于DBN的分类算法更符合人类专家的分类方式。
将表 2的油膜、类油膜、海水的数据项看作矩阵,分别计算对应的Kappa系数。Kappa系数也是一种计算分类精度方法,是综合了用户精度(类别精度)和制图精度两个角度的一个最终指标。在遥感图像处理中主要用来评价分类判断的精确性,Kappa系数仅适用于行数和列数相等的方阵[16]。Kappa系数值的范围在[-1,+1]之间,分为5个等级,其中0.61~0.80具有较好的一致性;0.81~1一致性最高。总分类精度和Kappa系数的区别在于总分类精度只考虑了正确分类的样本精度,而Kappa系数既考虑了正确分类的样本数量,同时也考虑了误分样本和漏分样本数量。计算方法如下:
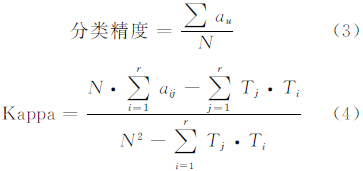
式中,aij表示方阵A的对角线元素及正确分类的数目;N为各类样本总量;Ti、Tj分别表示A的第i行与第j列之和。
通过表 3对DBN和NN分类准确率及Kappa系数作比较。
| 分类方法 | 油膜 | 类油膜 | 海水 | 分类精度 | Kappa系数 |
| DBN/% | 95.36 | 83.93 | 91.79 | 90.36 | 0.885 3 |
| NN/% | 95.36 | 80.36 | 85.43 | 87.38 | 0.844 4 |
由表 3中可以看出,类油膜在三类样本中分类准确率较低,对总分类精度产生了一定影响。DBN在各类样本的分类准确率及总分类精度上要高于NN。从Kappa系数上分析,DBN的分类结果具更很高的一致性。因此,DBN在实验中所获得的分类准确率能够较好地满足海上溢油SAR遥感图像分类的需求,且在网络的收敛时间和效率上也略胜于NN。
虽然利用不同的数据集对不同的算法进行比较是不合适的。但是为了与其他算法进行比较,本文选取溢油识别领域,特别是针对没有作预处理直接识别溢油的算法进行比较。Lena等运用基于区域的广义似然比(GLRT)来直接检测油膜[17]。Konstantinos等应用决策树的智能计算方法方法区分油膜与类油膜[18]。Fabio等应用NN对油膜进行半自动识别[19]。
表 4对以上几种算法的分类准确率进行了对比,唯有本文所提出的方法的准确率达到最高90.36%。从算法的执行效率上来看,本文方法未对图像做任何与处理,可以直接对SAR原始图像进行操作,提高了溢油识别算法的运算效率,检测方法更加可行。
| 对比方法 | 准确率/% |
| 基于DBN与TUGLCM特征* | 90.36 |
| 基于NN与TUGLCM特征* | 87.38 |
| GLRT | 88.61 |
| 基于决策树的智能计算 | 84.8 |
| NN | 83.5 |
| 注:*表示使用相同样本。 | |
本文模仿人类专家识别油膜、类油膜及海水的方式,提出一种针对原始溢油SAR图像进行识别的算法。该算法通过分析油膜的纹理特征,运用深度信念网络的方法对油膜进行识别。对于溢油SAR图像,选取5个灰度共生矩阵特征和4个Tamura特征,通过对样本的分析得到36维的特征向量。并且通过实验确定了DBN分类中的关键参数。实验结果表明,本文方法能够有效地将油膜、类油膜及海水区分开来,是一种高效可行性的溢油检测算法。
| [1] | Ma Long,Li Ying,Niu Ying. Research on SAR Oil Spill Monitoring by SVM Based on Texture Features[J]. Navigation of China, 2010,33(1):75-79(马龙,李颖,牛莹. 结合纹理的支持向量机合成孔径雷达溢油监测[J]. 中国航海,2010,33(1):75-79) |
| [2] | Topouzelis K,Karathanassi V,Pavlakis P,et al. Oil Spill Detection Using Netural Netwrks and SAR Data[C].The 20th ISPRS Congress,Istanbul,2004 |
| [3] | Zhao Dakang. Synthetic Aperture Radar Image Classification Based on Neural Networks[J]. Science Information, 2006(7):5-8(赵大康.基于神经网络的合成孔径雷图像分类研究[J].科技信息,2006(7):5-8) |
| [4] | Shi Lijian,Zhao Chaofang,Liu Peng. Oil Spill Identification in Marine SAR Images Based on TextureFeature and Artificial Neural Network[J]. Periodical of Ocean University of China,2009,39(6): 1 269-1 274(石立坚,赵朝方,刘朋.基于纹理分析和人工神经网络的SAR图像中海面溢油识别方法[J]. 中国海洋大学学报,2009,39(6):1 269-1 274) |
| [5] | Mansor S B, Assilzadeh H, IbrahimH M, et al. Oil Spill Detection and Monitoring from Satellite Image [OL]. http:// www.Gisdevelopment.net/appli2cation/miscellaneous,2014 |
| [6] | He Chu,Liu Ming. A Hierarchical Classification Method Based on Feature Selection and Adaptive Decision Tree for SAR Image[J]. Geomatics and Information Science of Wuhan University,2012,37(1):46-49(何楚,刘明.利用特征选择自适应决策树的层次SAR图像分类[J].武汉大学学报·信息科学版,2012,37(1):46-49) |
| [7] | Wu Zhaocong,Ouyang Qundong,Hu Zhongwen. Polarimetric SAR Image Classification Using Watershed-Transformation and Support Vector Machine [J]. Geomatics and Information Science of Wuhan University,2012,37(1):7-10(巫兆聪,欧阳群东,胡忠文.应用分水岭变换与支持向量机的极化SAR图像分类[J].武汉大学学报·信息科学版, 2012,37(1):7-10) |
| [8] | Tamura H,Mori S,Yamawaki T. Textural Features Corresponding to Visual Perception[J]. IEEE Transaction on Systems,1978,8(6):460-473 |
| [9] | Utgoff P,Stracuzzi D. Many Layered Learning[J].Neural Computation,2002,14(10):2 497-2 529 |
| [10] | Bengio Y,Lecun Y. Scaling Learning Algorithms Towards AI[J].Large-Scale Kernel Machines,2007,1:1-41 |
| [11] | G E. Hinton,S Osindero,Yee W. Teh. A Fast Learning Algorithm for Deep Belief Nets[J]. Neural Comput, 2006,18(7):1 527-1 554 |
| [12] | Bengio Y,Delalleau O. On the Expressive Power of Deep Architectures [C]. The 14th International Conference on Discovery Science, Berlin,2011 |
| [13] | Bengio Y,Lecun Y. Scaling Learning Algorithms Towards AI[M]. Cambridge: MIT Press,2007: 321-358; 599-619 |
| [14] | Xiao Hanguang, Cai Congzhong. Comparison Study of Normalization of Feature Vector[J]. Computer Engineering and Applications,2009,45(22):117-119(肖汉光,蔡从中. 特征向量的归一化比较性研究[J]. 计算机工程与应用,2009,45(22):117-119) |
| [15] | Zhou Shusen, Chen Qingcai, Wang Xiaolong. Active Deep Learning Method for Semi-supervised Sentiment Classification[J]. Neurocomputing, 2013, 120: 536-546 |
| [16] | Wang Jun. Estimation of the Kappa Coefficient from Consistency[D]. Chengdou: Sichuan University, 2006(王军. Kappa系数在一致性评价中的应用研究[D].成都:四川大学,2006) |
| [17] | Lena Chang, Tang Z S, Chang S H, et al. A Region-based GLRT Detection of Oil Spills in SAR Images[J]. Pattern Recognition Letters, 2008,29: 1 915-1 923 |
| [18] | Konstantinos T, Apostolos P. Oil Spill Feature Selection and Classification Using Decision Tree Forest on SAR Image Data[J]. ISPRS Journal of Photogrammetry and Remote Sensing,2012, 68: 135-143 |
| [19] | del Frate F, Petrocchi A, Lichtenegger J, et al. Neural Networks for Oil Spill Detection Using ERS-SAR Data[J]. IEEE Transactions on Geoscience and Remote Sensing, 2000,38(5): 2 282-2 287 |
 2016, Vol. 41
2016, Vol. 41


