文章信息
- 曾小牛, 李夕海, 刘志刚, 杨晓君, 刘代志
- ZENG Xiaoniu, LI Xihai, LIU Zhigang, YANG Xiaojun, LIU Daizhi
- 低纬度磁异常化极及分量换算的正则化方法
- Regularization Method for Reduction to the Pole and Components Transformation of Magnetic Anomaly at Low Latitudes
- 武汉大学学报·信息科学版, 2016, 41(3): 388-394
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 388-394
- http://dx.doi.org/10.13203/j.whugis20140342
-
文章历史
- 收稿日期: 2015-01-13

磁探测技术能快速而有效地探测出水下磁性目标,在沉船、水雷、海底电缆、未爆爆炸物和水下潜行器探测中有极为广泛的应用[1, 2, 3, 4, 5, 6, 7, 8, 9]。磁性体产生的磁场,除了受其本身的形态影响外,还受地球磁化场的影响。在低纬度地区,观测所得的磁场形态要比在高磁纬度地区相同目标体形态下复杂得多。具体表现为磁异常远比目标体本身形态复杂,负异常明显,伴生异常增多,而在高磁纬度地区,异常的分布形态与目标体形态的对应关系要好得多。化磁极工作就是设法消除倾斜磁化造成磁异常的复杂性,使磁异常的解释相对简单化[10]。同时,地磁场和磁性目标引起的磁异常都是矢量场,通常用3个坐标轴上的分量表示。理论分析和实践表明,磁异常的矢量信息能更全面地反映磁性目标的磁场特征,从而更准确地确定磁性目标的相关参数[4, 5, 6, 11, 12]。随着磁探测需求的不断提高,对磁异常分量换算的精度要求也越来越高。
本文通过分析发现,总强度磁异常分量换算算子和化极算子一样,同属放大型转换算子,其数值直接依赖于磁化倾角。磁纬度越低,磁化倾角绝对值越小,分量换算算子和化极算子的放大作用越强。在磁赤道地区,放大作用达到极点,变为不稳定算子。因此,在低磁纬度地区,磁异常化极和分量换算要比中高磁纬度地区的复杂很多。因此,本文采用Tikhonov正则化方法来求解低纬度磁异常化极和分量换算。同时,提出了一种基于径向平均功率谱估计磁异常噪声水平的方法,并进而利用偏差准则来后验确定正则化方法的正则参数。模型验证试验表明,正则化方法能够有效解决低纬度磁异常化极和分量换算的不稳定性,取得较好的转换效果。
1 磁异常化极及分量换算原理磁异常化极和分量运算既可在空间域进行,也可在频率域中完成,但是考虑到频率域可以将空间域复杂的褶积关系转化为频率域简单的乘积关系,并可以将各种转换统一到一个通用表达式中[8],因此,多数研究人员倾向于在频率域中完成各种转换运算。
由于现在经常测量的是总强度磁异常ΔT(总场强度在文献[12]中也有研究),其对应的测量方向就是地磁场方向。假设磁化强度方向与地磁场方向一致,且不考虑剩磁,则总强度磁异常ΔT化极(ΔT→Za⊥)和换算到三分量(ΔT→Xa、ΔT→Ya、ΔT→Za)的频域转换算子如下[10, 11, 12]:
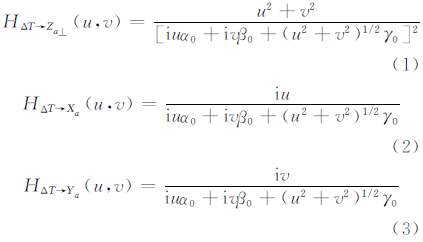
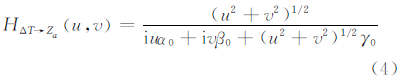
式中,u、v为x、y方向的圆频率;α0=cosIcosD;β0=cosIsinD;γ0=sinI为方向余弦,I、D分别为磁化方向的倾角和偏角。令u=rcosθ,v=rsinθ,代入式(1)~式(4),即可得极坐标系下的转换算子(取模):
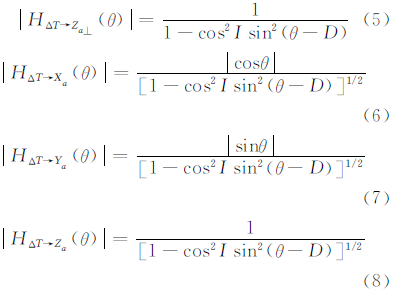
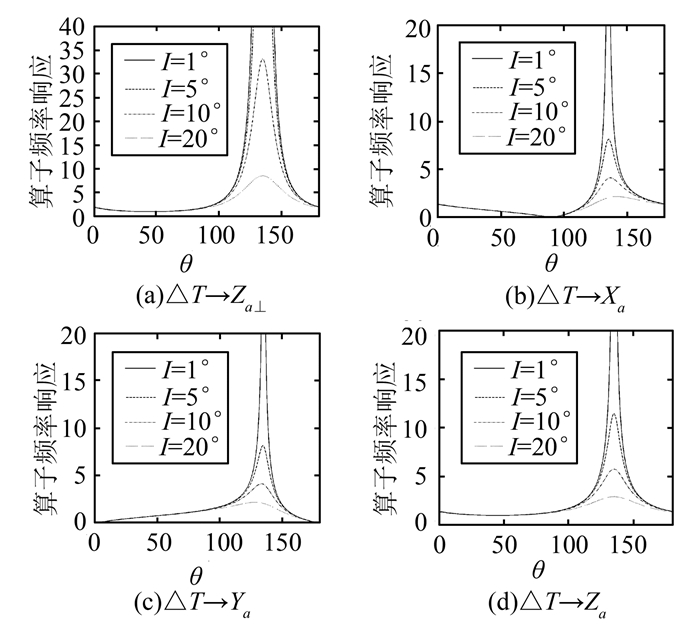
式中,θ=arctan(v/u);r为径向频率。由以上转换算子可以清楚看出,各算子是角度θ的单一函数,与频率的高低无关,其数值则直接依赖于磁倾角。当地磁倾角I很小时,cosI接近于1,此时如果θ接近于D±90°,则各转换算子的分母趋近0,上述转换算子变为不稳定算子。当D=45°时,各算子的频率响应随θ的变化如图 1(图中仅0≤θ≤180°,180° < θ≤360°部分具有对称性)。由图 1可知,化极算子的放大能力最强,三分量换算算子的放大能力稍弱,这表示在低纬度磁异常转换的实际应用中,化极算子最不稳定,分量换算算子也会放大噪声,但不像化极算子那么不稳定。
|
| 图 1 各转换算子的频率响应 Fig. 1 Frequency Response of Transform Operators |
设ΔT(u,v)和F(u,v)分别为总强度磁异常ΔT(x,y)和待求的转换量F(x,y)的频域表达形式,则它们在频域的关系可通过转换算子H(u,v)联系起来:

由于算子H(u,v)在低纬度的噪声放大效应,导致换算结果F(u,v)的不稳定。从数学上讲,该问题为线性不适定反问题[13]。对于求解形如式(9)的不适定问题,Tikhonov正则化是一种广泛应用的方法,它将式(9)的求解转化成如下的极小化问题:

式中,α为正则参数,用于平衡不稳定性及光滑性。式(10)的解为[13]:
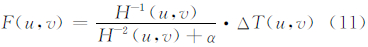
式(11)即为F(u,v)与ΔT(u,v)在频域转换的正则化关系式。
实施正则化方法的关键在于正则参数α的选取。正则化参数的选取,依据是否需要预先估计原始数据的噪声水平而分为后验和先验两类策略。L-曲线法[14]和广义交叉校验(GCV)法[15]是最常用的先验策略;Morozov偏差原理[16]是典型的后验策略。本文在提出一种基于径向功率谱估计噪声水平的基础上,采用偏差准则来后验选取正则参数。
2.2 基于径向谱的噪声水平估计文献[17]提出了径向平均功率谱的概念,并被广泛应用于位场(地磁场和重力场)数据处理[18, 19, 20]。磁异常径向平均功率谱的定义如下:设磁异常数据的功率谱为P(u,v),其在径向方向θ上的取值为P′(r,θ),则有:

当θ取定值时,P′(r,θ)仅是r的函数。求取径向平均功率谱的具体实施步骤如下。
1) 求磁异常功率谱;
2) 以磁异常功率谱的中心作圆,圆的半径分别为基频的整数倍,从而形成一系列环带;
3) 取环带内所有点的功率谱值作其平均值;
4) 以径向频率r为横坐标,各频带内功率谱平均值作为纵坐标(取对数坐标),即可得径向平均功率谱。
一个假想的径向平均功率谱如图 2所示。从图 2可知,如果假设观测噪声为白噪声,则与磁异常信号不相关的白噪声的功率谱应该为常数,即对应于图 2中的水平部分。这样,对于磁异常的径向平均功率谱,存在一个截止径向频率rc将磁异常信号谱和噪声谱大致分开。由此可以得到磁异常功率谱的等效噪声区域如图 3(仅显示1/4区域)。由以上讨论可知,利用Parseval定理[21],可以通过式(13)来近似估计磁异常噪声的方差:
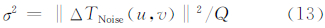
式中,ΔTNoise(u,v)表示等效噪声区域内相应磁异常ΔT(x,y)的Fourier变换结果;Q为等效噪声区域内的数据总数值。

|
| 图 2 径向平均功率谱示意图 Fig. 2 Schematic Diagram for the Radially Averaged Power Spectrum |
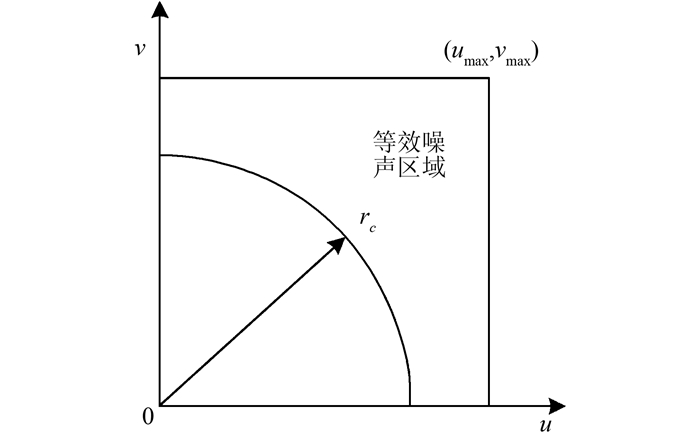
|
| 图 3 1/4部分等效噪声区域示意图 Fig. 3 Schematic Diagram for one Quadrant of the Equivalent Noise Region |
偏差原理的基本思想是,如果已知磁异常噪声的方差σ2,则最佳正则化参数α应该满足以下约束方程:
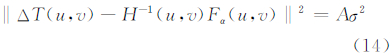
式中,Fα(u,v)为正则化参数取α时的磁异常正则化转换结果;A为磁异常总的数据个数。式(14)的物理意义是显然的,即转换误差应该同磁异常的噪声水平一致。在实际应用中,可构建如下的偏差函数来求解最佳正则化参数。值得指出的是,在噪声方差可以获取或近似得到的情况下,偏差准则是十分有效的正则化参数选择方法[13]。
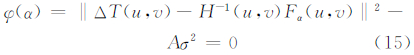
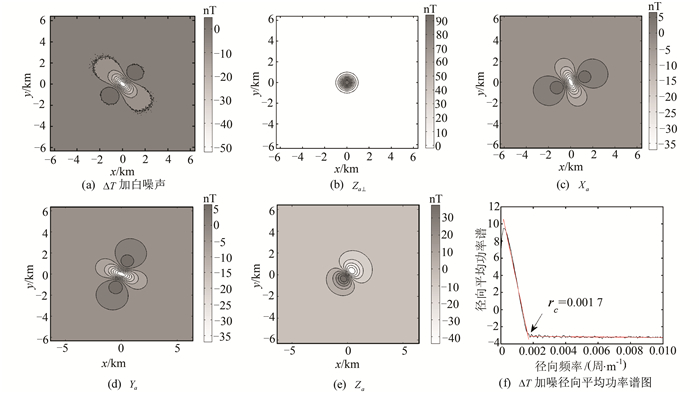
为检验磁异常分量换算方法的有效性,采用单个球体仿真磁异常数据进行分析(多目标磁异常分量换算在文献[12]中有研究)。设磁性球体半径为500 m,球体中心点的x、y坐标均为0,埋深为1 000 m,磁化强度为1 A/m,其倾角和偏角分别为I=1°与D=45°。线数M和点数N同为256,点线距都为50 m。根据球体总强度磁异常解析表达式[8]计算了z=0平面上的总强度磁异常ΔT,同时,为了接近实际情况,在ΔT中加入零均值、方差为0.04 nT的高斯白噪声,其结果如图 4(a)。无噪声条件下球体垂直磁化磁异常Za⊥和Xa、Ya、Za三分量的等值线分别如图 4(b)~4(e)所示。由图 4(b)可见,垂直磁化的磁异常和目标体的形态具有很好的对应性。计算含噪总强度磁异常ΔT(图 4(a))的径向平均功率谱,其结果如图 4(f)。通过功率谱形状分析可知(红线为径向谱中拟合得到的线性部分),可以将功率谱分为0~0.001 7和0.001 7~0.01两段,将前段视为信号部分,后一段近似视为噪声部分。如此,则可以确定功率谱的截止频率为rc=0.001 7。按式(13)求得的磁异常噪声方差为0.040 1 nT。可见,本文提出的磁异常噪声估计方法具有较高的精度,误差为0.25 %。
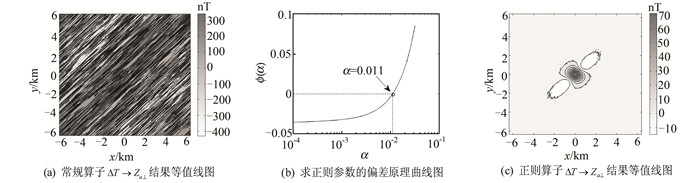
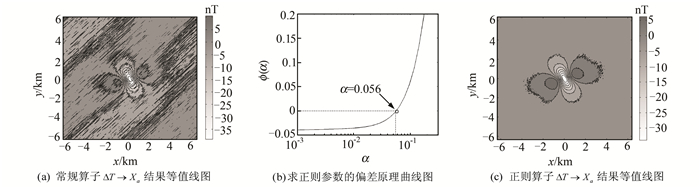
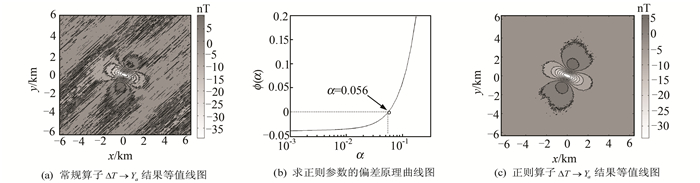
采用常规算子(式(1)~式(4))对图 4(a)所示含噪总强度磁异常ΔT进行化极和分量换算的结果分别如图 5(a)(ΔT→Za⊥)、图 6(a)(ΔT→Xa)、图 7(a)(ΔT→Ya)、图 8(a)(ΔT→Za)所示。在求得噪声方差后,利用式(15)求取正则化方法的最优正则化参数,分别如图 5(b)(ΔT→Za⊥)、图 6(b)(ΔT→Xa)、图 7(b)(ΔT→Ya)、图 8(b)(ΔT→Za)所示,对应的正则化化极和分量换算结果分别如图 5(c)(ΔT→Za⊥)、图 6(c)(ΔT→Xa)、图 7(c)(ΔT→Ya)、图 8(c)(ΔT→Za)所示。由图 5(a)和5(c)、图 6(a)和6(c)、图 7(a)和7(c)、图 8(a)和8(c)的对比可见:(1)常规化极和分量换算都存在磁南北方向的条带状干扰,其中化极的噪声放大能力最强,导致化极结果完全被噪声掩盖,分量换算结果虽然好于化极结果,但也存在较大噪声干扰,这与§2的算子频率响应分析结果是一致的;(2)低纬度正则化化极和分量换算算子对改善常规算子的噪声放大效应效果明显。
|
| 图 4 仿真球体磁异常等值线图及含噪总强度磁异常径向平均功率谱图 Fig. 4 Contours Map of the Magnetic Anomaly of Simulated Sphere Model and the Radially Averaged Power Spectrum for Total Field Magnetic Anomaly with Noise |
|
| 图 5 常规算子和正则算子ΔT→Za⊥对比 Fig. 5 Comparison of ΔT→Za⊥ for Conventional Operator and Regularization Operator |
|
| 图 6 常规算子和正则算子ΔT→Xa对比 Fig. 6 Comparison of ΔT→Xa for Conventional Operator and Regularization Operator |
|
| 图 7 常规算子和正则算子ΔT→Ya对比 Fig. 7 Comparison of ΔT→Ya for Conventional Operator and Regularization Operator |

|
| 图 8 常规算子和正则算子ΔT→Za对比 Fig. 8 Comparison of ΔT→Za for Conventional Operator and Regularization Operator |
为了定量分析磁异常分量的换算精度,将两类算子的化极和分量换算结果Fc(x,y)分别和理论值Ft(x,y)进行对比,并采用计算值与理论值之差的最大值、最小值、绝对均值和中误差作为精度评价指标,统计结果如表 1。中误差定义为:
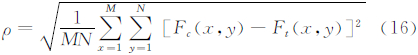
由表 1可以看出,正则算子转换的误差要比常规算子的小很多。表 2为模型倾角取I=0.5°时的常规算子和正则算子的化极及分量换算的误差对比。结合表 1可知:伴随倾角I的减少,常规算子的化极和分量换算误差增大明显,尤其是化极误差大幅增大,而正则算子的化极和分量换算误差依然能稳定在一定水平上。
| ΔT→Za⊥ | ΔT→Xa | ΔT→Ya | ΔT→Za | |||||
| 常规算子 | 正则算子 | 常规算子 | 正则算子 | 常规算子 | 正则算子 | 常规算子 | 正则算子 | |
| 最大值 | 439.39 | 6.99 | 6.88 | 3.40 | 7.63 | 3.14 | 9.86 | 6.33 |
| 最小值 | -428.84 | -25.33 | -7.99 | -1.48 | -6.67 | -1.50 | -10.55 | -7.81 |
| 绝对均值 | 129.34 | 1.42 | 1.74 | 0.26 | 1.74 | 0.26 | 2.43 | 1.25 |
| 中误差 | 153.95 | 2.65 | 2.10 | 0.37 | 2.10 | 0.37 | 2.96 | 1.58 |
| ΔT→Za⊥ | ΔT→Xa | ΔT→Ya | ΔT→Za | |||||
| 常规算子 | 正则算子 | 常规算子 | 正则算子 | 常规算子 | 正则算子 | 常规算子 | 正则算子 | |
| 最大值 | 1 524.85 | 6.94 | 10.23 | 3.35 | 11.94 | 3.06 | 15.79 | 8.38 |
| 最小值 | -1 337.62 | -25.77 | -12.12 | -1.69 | -10.25 | -1.65 | -15.65 | -8.30 |
| 绝对均值 | 129.34 | 1.42 | 3.24 | 0.26 | 3.24 | 0.26 | 4.52 | 1.68 |
| 中误差 | 153.95 | 2.65 | 3.81 | 0.36 | 3.81 | 0.37 | 5.39 | 2.10 |
1) 本文分析了总强度磁异常化极算子和分量换算算子的频域特性,得出它们在低纬度存在噪声放大效应的结论。
2) 采用Tikhonov正则化方法来消除低纬度磁异常转换算子的噪声放大效应,并提出了一种估计磁异常噪声水平的方法,进而实现了基于后验策略的正则化方法正则参数选择方法。
3) 利用球体模型对常规算子和正则算子进行了低纬度磁异常化极和分量换算对比试验,试验结果验证了所提噪声估计方法的有效性和正则化方法的优越性。
| [1] | Marchetti M, Sapia V, Settimi A. Magnetic Anomalies of Steel Drums: A Review of the Literature and Research Results of the INGV[J]. Annals of Geophysics, 2013, 56(1): R0108 |
| [2] | Li Y, Devriese S G R, Krahenbuhl R A, et al. Enhancement of Magnetic Data by Stable Downward Continuation for UXO Application[J].IEEE Transactions on Geoscience and Remote Sensing, 2013, 51(6): 3 605-3 614 |
| [3] | Yu Bo, Liu Yanchun, Bian Gang, et al. Magnetism Detecting Method for Seabed Cable in Marine Engineering Surveying[J]. Geomatics and Information Science of Wuhan University, 2006, 31(5): 454-457 (于波, 刘雁春, 边刚, 等. 海洋工程测量中海底电缆的磁探测法[J]. 武汉大学学报·信息科学版, 2006, 31(5): 454-457) |
| [4] | Bian Guanglang, Zhai Guojun, Liu Yanchun, et al. The Parameters Determination of Magnetic Spherical Object Based on Laplace Approach[J]. Chinese Journal of Geophysics, 2011, 54(3): 787-792 (卞光浪, 翟国君, 刘雁春, 等. 基于Laplace法的磁性球体参数确定[J]. 地球物理学报, 2011, 54(3): 787-792) |
| [5] | Bian Guanglang, Zhai Guojun, Fan Long, et al. Applying Two-step Iterative Least Square Approach to Determine the Geometry and Physical Parameters of Magnetic Sphere Sources[J]. Chinese Journal of Geophysics, 2011, 54(5): 1 357-1 383 (卞光浪, 翟国君, 范龙, 等. 用最小二乘两步迭代法求解磁性球体几何与磁性参数[J]. 地球物理学报, 2011, 54(5): 1 357-1 383) |
| [6] | Bian Guanglang, Zhai Guojun, Liu Yanchun, et al. Computation of Spatial Position Parameters of Magnetic Object with Improved Euler Approach[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(3): 386-392 (卞光浪, 翟国君, 刘雁春, 等. 应用改进欧拉算法解算磁性目标空间位置参数[J]. 测绘学报, 2011, 40(23): 386-392) |
| [7] | Huang Yu. Geomagnetic Field Measurement and Study on Underater Magnetic Localization Technology[D]. Harbin: Harbin Engineering University, 2011 (黄玉. 地磁场测量及水下磁定位技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2011) |
| [8] | Bian Guanglang, Zhai Guojun, Huang Motao, et al. Inversion of the Parameters of 3D Magnetic Body with Its Magnetic Profile Lines[J]. Geomatics and Information Science of Wuhan University, 2012, 37(1): 91-95 (卞光浪, 翟国君, 黄谟涛, 等. 利用剖面测线磁场数据反演三度磁性体参数[J]. 武汉大学学报·信息科学版, 2012, 37(1): 91-95) |
| [9] | Liu Fanming, Zhang Yingfa, Jing Xin, et al. Fast Computation of Derivatives of Magnetic Vector Components in Magnetic Anomaly Detection[J]. Geomatics and Information Science of Wuhan University, 2014, 39(9): 1 091-1 097 (刘繁明, 张迎发, 荆心, 等. 磁异常探测中磁场矢量导数快速计算方法[J]. 武汉大学学报·信息科学版, 2014, 39(9): 1 091-1 097) |
| [10] | Guan Zhining. Magnetic Field and Magnetic Exploration[M]. Beijing: Geological Press, 2005(管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005) |
| [11] | Bian Guanglang, Zhai Guojun, Liu Yanchun, et al. Components Conversion of Magnetic Anomaly in Detecting Underwater Magnetic Object[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(2): 232-237 (卞光浪, 翟国君, 刘雁春, 等. 水下磁性目标探测中磁异常分量换算方法 [J]. 测绘学报, 2011, 40(2): 232-237) |
| [12] | Bian Guanglang, Zhai Guojun, Huang Motao, et al. Transformation of Multi-objects Magnetic Anomaly Components with Geomagnetic Effect[J]. Geomatics and Information Science of Wuhan University, 2011, 36(8): 914-918 (卞光浪, 翟国君, 黄谟涛, 等. 顾及地磁背景场的多目标磁异常分量换算方法[J]. 武汉大学学报·信息科学版, 2011, 36(8): 914-918) |
| [13] | Wang Yanfei. Computational Methods for Inverse Problems and Their Applications[M]. Beijing: Higher Education Press, 2007 (王彦飞. 反演问题的计算方法及其应用[M]. 北京: 高等教育出版社, 2007) |
| [14] | Hansen P C, O'Leary D P. The Use of the L-curve in the Regularization of Discrete Ill-posed Problems[J]. SIAM Journal on Scientific Computing, 1993, 14(6): 1487-1503 |
| [15] | Golub G H, Heath M, Wahba G. Generalized Cross-validation as a Method for Choosing a Good Ridge Parameter[J].Technometrics, 1979, 21(2): 215-223 |
| [16] | Morozov V A. Methods for Solving Incorrectly Posed Problems[M]. New York: Springer-Verlag, 1984 |
| [17] | Spector A, Grant F S. Statistical Models for Interpreting Aeromagnetic Data[J].Geophysics, 1970, 35(2): 293-302 |
| [18] | Stefan M, Vijay D. Potential Field Power Spectrum Inversion for Scaling Geology[J]. Journal of Geophysical Research, 1995, 100(B7): 12 605-12 616 |
| [19] | Ravat D, Pignatelli A, Nicolos I, et al. A Study of Spectral Methods of Estimating the Depth to the Bottom of Magnetic Sources from Near-surface Magnetic Anomaly Data[J].Geophysical Journal International, 2007, 169(2): 421-434 |
| [20] | Guo L H, Meng X H, Chen Z X, et al. Preferential Filtering for Gravity Anomaly Separation[J].Computers & Geosciences, 2013, 51: 247-254 |
| [21] | Mitra S K, Kuo Y. Digital Signal Processing: a Computer-based Approach[M]. New York: McGraw-Hill, 2006 |
 2016, Vol. 41
2016, Vol. 41


