文章信息
- 薛树强, 杨元喜
- XUE Shuqiang, YANG Yuanxi
- 最小GDOP组合Walker星座构型
- Combined Walker Configurations with Minimal GDOP
- 武汉大学学报·信息科学版, 2016, 41(3): 380-387
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 380-387
- http://dx.doi.org/10.13203/j.whugis20130485
-
文章历史
- 收稿日期: 2014-10-11

2. 中国测绘科学研究院, 北京, 100830;
3. 地理空间信息工程国家重点实验室, 陕西 西安, 710054
2. Chinese Academy of Surveying and Mapping, Beijing 100830, China;
3. National Key Laboratory for Geo-information Engineering, Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China
控制网的一类设计是确定控制网的最佳定位图形[1]。定位图形设计与测量平差具有同样的地位和重要性[2]。控制网常用的准则有A-准则、N-准则、S-准则和D-准则[1]。在导航定位中,位置及钟差参数的精度与几何精度衰减因子(GDOP)有关[3, 4, 5]。GDOP的概念建立在A-准则的基础上,即点位方差-协方差矩阵的对角线元素之和作为网的精度指标[6]。文献[7, 8, 9, 10, 11, 12]讨论了测距单点定位构型的最小GDOP取值,文献[6]探讨了4颗卫星情形下具有最小GDOP的测距单点定位构型。顾及精度和可靠性的控制网优化设计思想在现实应用中具有重要参考价值[10, 11, 13]。文献[14]给出了具有两个自由度的最小PDOP平面交会定位图形的完整解。
图论为定位图形的表示和分析提供了数学模型[15, 16, 17, 18, 19]。文献[18]基于图论建立了连续定位构型,并使用D-准则建立了动态控制点的最佳运动曲线,即通过时间积分解决了定位构型分析。文献[15]借助傅立叶中的正交三角函数系统研究了最小GDOP单点定位构型,导出了最小GDOP定位构型的图形条件,并以此给出了一些具有最小GDOP测距单点定位构型解。文献[16]基于圆锥构型构造了一种嵌套圆锥构型,得到了一族具有丰富几何结构的最小GDOP三维定位构型,并由此导出了数学中的5种正多面体构型,证明了数学中的5种正多面体均具有最小的GDOP。
组合GNSS星座可为地球科学研究提供空间分辨率和时间分辨率更高[5]。特别的,正在兴起的BDS(北斗导航卫星定位系统)采用混合星座[3],在传统Walker构型的基础上引入GEO卫星轨道和IGSO卫星轨道。因此,讨论最小GDOP组合Walker构型,在单GNSS星座设计、多GNSS星座组合优化等方面具有重大现实意义。本文借助于图论表示法,将GNSS普遍采用的Walker构型扩展为组合Walker构型,并在文献[15, 16]的基础上,导出了最小GDOP组合Walker构型所应满足的条件方程。讨论了单一和组合Walker构型的GDOP地表覆盖性质。
1 最小GDOP三维单点定位构型“定位构型”是指定位系统的所有可能的状态,是待定点与控制点构成的定位图形[15]。在m (m=2或3)维空间中,由未知点x和已知点xi (i=1,2,…,n)构成的定位图形可以使用图论模型化为[15, 17]:

式中,Θ={xi|i=1,2,…,n},为控制点构型。 由最小GDOP测距单点定位构型全体构成的集合
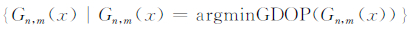
称为GDOP最小测距单点定位构型集。其中,n表示控制点数目;m表示定位图形所在空间的维数;GDOP为定位构型Gn,m(x)的GDOP,argmin为GDOP极值目标函数。最小GDOP测距单点定位构型具有以下性质[15]:
(1) 叠加(加法)不变性。对任意自然数q1和q2,若Gq1,m(x)∈Oq1,m(x),Gq2,m(x)∈Oq1,m(x),则叠加构型Gq1,m(x)+Gq2,m(x)∈Oq1+q2,m(x)。
(2) 旋转不变性(最小DOP定位构型的旋转不变性反映了定位构型的DOP与坐标系统的选取无关)。若Gn,m(x)∈On,m(x),则Gn,m(x)的n控制点围绕待定点x旋转一定角度(由旋转矩阵R确定)后的定位构型Gn,mR(x)∈On,m(x)。
文献[15]构造了4种三维最小GDOP测距单点定位构型。笛卡尔构型和Walker构型的最小GDOP图形条件可为GNSS星座设计提供参考。文献[16]从最小GDOP嵌套圆锥构型中导出了数学中仅有的5种正多面体构型:正四面体、立方体、正八面体、正二十面体和正十二面体,证明了这5种正多面体构型满足GDOP极值条件。因卫星的运动轨迹不是自由曲线,而要遵循牛顿运动定律,圆锥构型并不能很好地适用于卫星星座设计。笛卡尔构型和Walker构型可满足单卫星星座设计需求,但这仍不能满足组合Walker星座设计和混合星座设计,例如,在北斗MEO卫星星座采用Walker构型,同时还混入了地球同步卫星轨道和倾斜地球同步轨道。
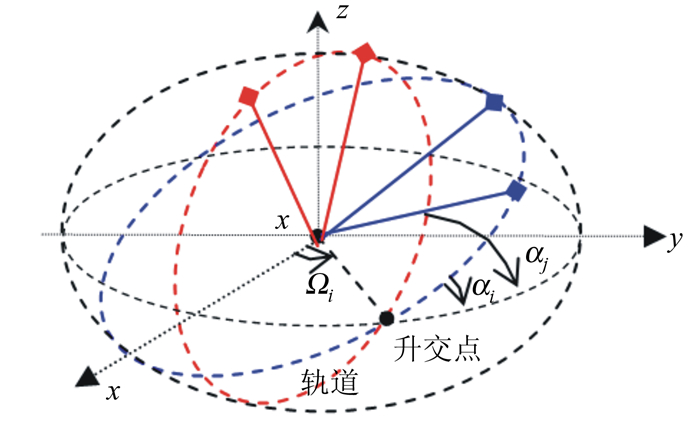
2 组合Walker构型如图 1所示,在T个与x-o-y坐标平面夹角均为α的平面内,存在n个最小GDOP二维测距单点定位构型G1n,2(x)∈On,2(x),G2n,2(x)∈On,2(x),…,Gn,2T(x)∈On,2(x),若这T个平面中的任意相邻平面间夹角均等于γ=2π/T(等分圆周),即有[20]:
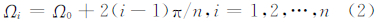
则这n个二维定位构型构成的三维定位构型记为WnT,3α,T,F(x),其中符号W来自于单词“Walker”的首字母。为改善星座的地表覆盖,可通过设置不同轨道平面内卫星的初始相位。GNSS星座则常通过引入调相因子F改善地表覆盖,可将该Walker构型记为 (x)。文献[15]证明,
(x)。文献[15]证明, (x)∈OnT,3(x)。GPS卫星星座轨道倾角恰为55°≈arctan√2。
(x)∈OnT,3(x)。GPS卫星星座轨道倾角恰为55°≈arctan√2。
|
| 图 1 组合Walker构型 Fig. 1 Combined Walker Configuration |
若将S个Walker构型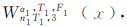
 叠加构成的定位构型称为组合Walker构型,则该构型可记为:
叠加构成的定位构型称为组合Walker构型,则该构型可记为:

式中,∪表示求并集合。
3 组合Walker构型的GDOP极值下面将推导组合Walker构型在地心处GDOP极值的一般条件(由于地球半径相对于卫星轨道较小,则当地心GDOP达到极值时,地表GDOP分布将相对均匀[17])。对于组合定位构型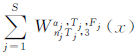 ,其设计矩阵可表示为[15]:
,其设计矩阵可表示为[15]:
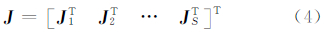
式中,Jj是第j个单Walker定位构型的设计矩阵。若设

则由文献[15]导出的公式(47),可得:
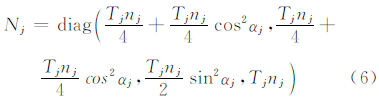
结合式(4),由式(6)可得:
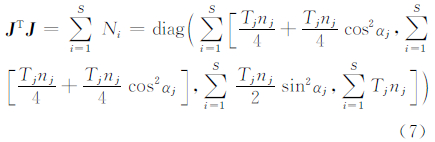
记Mj=Tjnj为第j个单Walker构型的总数,则由文献[15]导出的GDOP极值条件,可得:
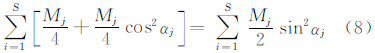
化简式(8)可得:
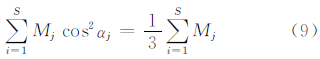
显然,条件方程(9)为欠定方程,唯一确定最小GDOP组合构型的几何条件需要给出一定的条件。此外,当调相因子F=0时,Walker构型可退化为组合圆锥构型。
4 最小GDOP组合Walker构型对比文献[16]中的条件方程(19)可以发现,最小GDOP嵌套圆锥构型张角条件与最小GDOP组合Walker构型倾角条件完全相同。为便于记忆,给出了GDOP最小正多面体支撑Walker构型。
4.1 正多面体支撑Walker构型(1) 正四面体支撑Walker构型
令S=2,M2=3M1,cos2α1=1(极轨道),则由式(9)可得:当cos2α2=1/9(α2≈±19.47°)时, 。
。
(2) 正方体支撑Walker构型
令S=1,则由式(9)可得,当cos2α=1/3(α≈±54.74°)时,可导出正方体支撑Walker构型,该构型显然与单卫星构型 (x)∈OnT,3(x)具有相同的结构。
(x)∈OnT,3(x)具有相同的结构。
(3) 正八面体支撑Walker构型
令S=2,M2=2M1,令α1=0(赤道平面轨道),则由式(9)可得,当α2=90°时,则正八面体支撑Walker构型 ∈O3n1T1,3(x)。
∈O3n1T1,3(x)。
(4) 正二十面体支撑Walker构型
令S=2,M2=5M1,令α1=0(赤道平面轨道),则由式(9)可得,当cos2α2=1/5(α2≈±63.44°)时,则正二十面体支撑Walker构型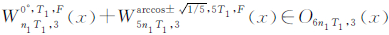 。
。
(5) 正十二面体支撑Walker构型
令S=2,M1=M2,则由式(9)可得,当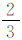 =cos2α1+cos2α2时,总存在
=cos2α1+cos2α2时,总存在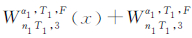 (x)∈O2n1T1,3(x)。类似文献[16],由cos2α1=
(x)∈O2n1T1,3(x)。类似文献[16],由cos2α1= 可得正十二面体支撑Walker构型。
可得正十二面体支撑Walker构型。
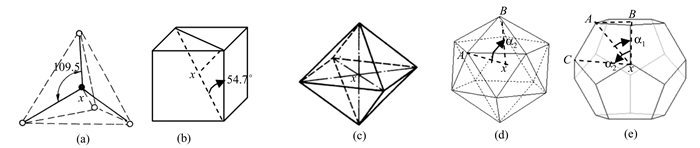
|
| 图 2 正多面体构型 Fig. 2 Regular Polyhedrons Configuration |
令S=2,α1=90°,则由条件式(9)可得:

当且仅当

时,式(10)中的α2存在实数解。例如,正四面体支撑Walker构型和正八面体支撑Walker构型均含一个极轨Walker构型(轨道倾角为90°的Walker构型),且显然满足条件(11)。
当S=2时,存在无穷种含有极轨Walker构型的最小GDOP组合Walker构型,且

可见,引入一个极轨Walker构型后,另外一个Walker构型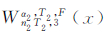 的轨道倾角应在最小GDOP 单Walker构型
的轨道倾角应在最小GDOP 单Walker构型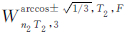 (x)∈On2T2,3(x)的基础上对卫星轨道倾角进行适当调整(调减卫星轨道倾角),以确保组合后的Walker构型仍满足GDOP极值条件。正八面体支撑Walker构型给出了这种调整的极限情形。
(x)∈On2T2,3(x)的基础上对卫星轨道倾角进行适当调整(调减卫星轨道倾角),以确保组合后的Walker构型仍满足GDOP极值条件。正八面体支撑Walker构型给出了这种调整的极限情形。
类似地,当S>2时,还可以导出许多含有极轨Walker构型的最小GDOP组合Walker构型。
4.3 含有赤道平面轨道的组合Walker构型令S=2,α1=0°,则由条件式(9)可得:
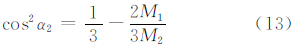
当且仅当
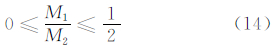
时,式(13)中的α2存在实数解。例如,正八面体支撑Walker构型和正二十面体支撑Walker构型均含一个赤道平面Walker定位构型(轨道倾角为0时的Walker构型),且显然满足条件(14)。
由式(13)可得:

可见,在赤道平面引入零倾角的Walker构型后,另一个Walker构型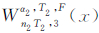 的轨道倾角应在最小GDOP 单Walker构型
的轨道倾角应在最小GDOP 单Walker构型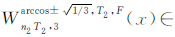 On2T2,3(x)的基础上对轨道倾角进行适当调整(调增轨道倾角),以确保组合后的Walker构型仍满足GDOP极值条件。正八面体支撑Walker构型给出了这种调整的极限情形。
On2T2,3(x)的基础上对轨道倾角进行适当调整(调增轨道倾角),以确保组合后的Walker构型仍满足GDOP极值条件。正八面体支撑Walker构型给出了这种调整的极限情形。
通过仿真分析,应用条件方程(9)讨论GNSS星座构型设计与星座构型二次设计。仿真基于以下假设:
① Walker构型采用MEO卫星,轨道高度采用20 000 km,第一个轨道面的升交点角距设为0°,即式(2)中的Ω0=0;
② 设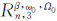 表示由n颗卫星在轨道平面内均匀分布构成的倾角为β的单卫星轨道(ω0、Ω0为第一颗卫星的初始相位和轨道的升交点角距);
表示由n颗卫星在轨道平面内均匀分布构成的倾角为β的单卫星轨道(ω0、Ω0为第一颗卫星的初始相位和轨道的升交点角距);
③ GEO卫星高度设为36 000 km;
④ 地球半径设为6 378.1 km;
⑤ 将地表分为5 120个三角形,计算各三角形中心点处的GDOP(历元t=0时);
⑥ 设高度角大于0时,卫星可见。
在上述假设下,地表的平均GDOP定义为:
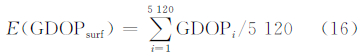
式中,GDOPi是第i个三角形中心点处的GDOP。地表GDOP的方差定义为:
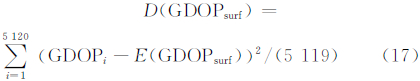
地表最大GDOP取值定义为:

表 1和图 3分别给出了 、
、 、
、 、
、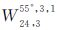 、
、 和
和 等6种Walker星座构型所对应的地表GDOP分布情况。从表 1给出的统计结果中可以发现,调相因子对改善地表GDOP均值和方差均有帮助,但会增大地表最大GDOP的取值。当调相因子为0且不考虑卫星不可见时,构型
等6种Walker星座构型所对应的地表GDOP分布情况。从表 1给出的统计结果中可以发现,调相因子对改善地表GDOP均值和方差均有帮助,但会增大地表最大GDOP的取值。当调相因子为0且不考虑卫星不可见时,构型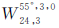 在地心的GDOP较为接近其理论最小值,且地表GDOP的最大值最小,但其GDOP的最小值和方差均相比较大。当调相因子为1时,构型
在地心的GDOP较为接近其理论最小值,且地表GDOP的最大值最小,但其GDOP的最小值和方差均相比较大。当调相因子为1时,构型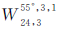 在地心的GDOP、地表GDOP均值、地表GDOP方差、地表最大GDOP均相对较小。对于单卫星系统星座而言,北斗的MEO卫星星座采用
在地心的GDOP、地表GDOP均值、地表GDOP方差、地表最大GDOP均相对较小。对于单卫星系统星座而言,北斗的MEO卫星星座采用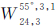 ,从GDOP角度北斗星座优于GLONASS。
,从GDOP角度北斗星座优于GLONASS。
| 星座构型 | E(GDOP″surf) | D(GDOP″surf) | max(GDOP″surf) |
 | 1.824 648 | 0.156 944 | 2.777 694 |
 | 1.805 554 | 0.126 788 | 2.799 434 |
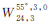 | 1.868 698 | 0.203 468 | 2.716 875 |
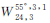 | 1.790 041 | 0.104 520 | 2.772 505 |
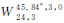 | 1.845 958 | 0.187 242 8 | 2.949 810 |
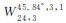 | 1.803 867 | 0.120 335 | 3.029 442 |
如图 3所示,地表GDOP分布的划分具有很强的规律性,且轨道倾角不改变这种划分,而仅改变划分的GDOP取值。因此,相比GNSS星座采用相同的最优轨道倾角(约为55°),借助本文导出的条件方程(9),通过组合具有不同轨道倾角的Walker星座,更有利于改善地表GDOP分布的均匀性。
5.2 GLONASS星座二次设计利用式(9)可给出多种二次设计方案,下面仅讨论以下两种方案。
方案1 在GLONASS中引入一个由24颗卫星构成的Walker星座,则由式(9)可得:

即当θ=45.837 9°时,组合星座最优。星座 和
和 的地表GDOP分布情况由图 3(e)、3(f)给出。
的地表GDOP分布情况由图 3(e)、3(f)给出。
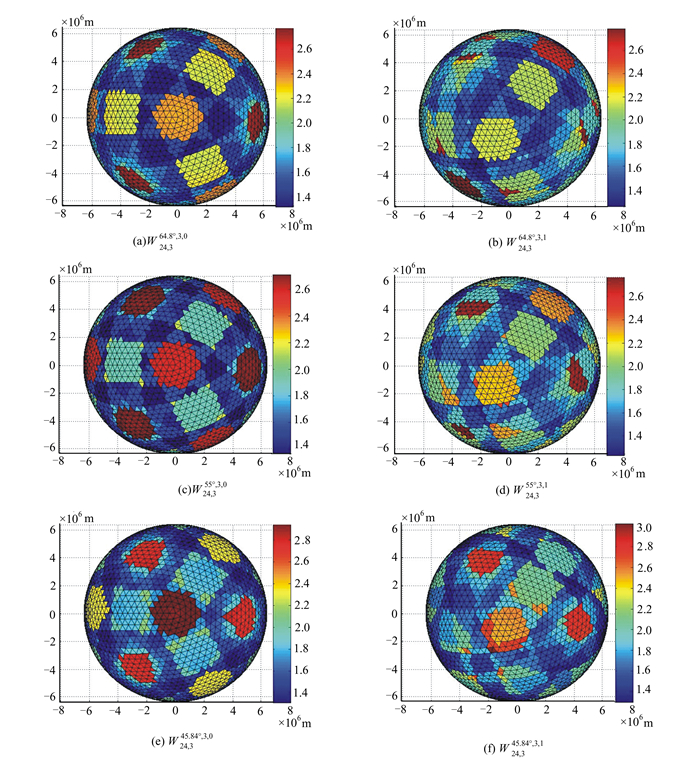
|
| 图 3 地表GDOP分布 Fig. 3 Distribution of Surface GDOP of the Earth |
为了验证方案1,仿真组合星座
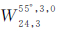 ,并计算地表GDOP分布。从图 4和表 2中可以发现,组合星座
,并计算地表GDOP分布。从图 4和表 2中可以发现,组合星座 的地表GDOP均值、方差和最大值均明显小于组合星座
的地表GDOP均值、方差和最大值均明显小于组合星座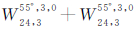 的相应统计量。这进一步验证了通过式(9)组合不同轨道倾角的Walker构型具有更优越的性能。
的相应统计量。这进一步验证了通过式(9)组合不同轨道倾角的Walker构型具有更优越的性能。
| 星座构型 | E(GDOP″surf) | D(GDOP″surf) | max(GDOP″surf) |
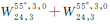 | 1.186 622 | 0.026 549 | 1.824 353 |
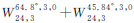 | 1.158 691 | 0.015 800 | 1.548 785 |

|
| 图 4 不同组合Walker构型的性能 Fig. 4 Performance of Different Combined Walker Configurations |
方案2 在GLONASS中引入静地卫星轨道,则由式(9)可得:
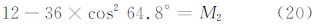
可得,M2=5.473 6,即当引入5~6颗GEO卫星时(由正二十面体支撑Walker构型也可以得到该结论),可改善GLONASS的地表GDOP分布。
为了验证方案2,仿真组合星座
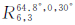 (
(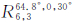 表示6颗均匀分布于倾角为64.8°的倾斜轨道面内,其升交点角距和初始相位分别为30°和0°)和星座
表示6颗均匀分布于倾角为64.8°的倾斜轨道面内,其升交点角距和初始相位分别为30°和0°)和星座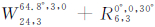 (
(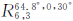 表示6颗均匀分布于赤道面的GEO卫星)。如表 3和图 5所示,对比上述两种组合星座的地表GDOP分布可得,组合星座
表示6颗均匀分布于赤道面的GEO卫星)。如表 3和图 5所示,对比上述两种组合星座的地表GDOP分布可得,组合星座
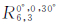 的地表GDOP均值、方差和最大值均明显小于组合星座
的地表GDOP均值、方差和最大值均明显小于组合星座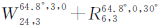 的相应统计量。这表明,要改善GLONASS星座的全球性能,应重点考虑引入小倾角卫星轨道。
的相应统计量。这表明,要改善GLONASS星座的全球性能,应重点考虑引入小倾角卫星轨道。
| 星座构型 | E(GDOP″surf) | D(GDOP″surf) | max(GDOP″surf) |
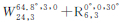 | 1.506 888 778 | 0.054 580 0 | 2.352 829 974 |
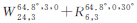 | 1.579 313 149 | 0.092 334 6 | 2.745 334 274 |
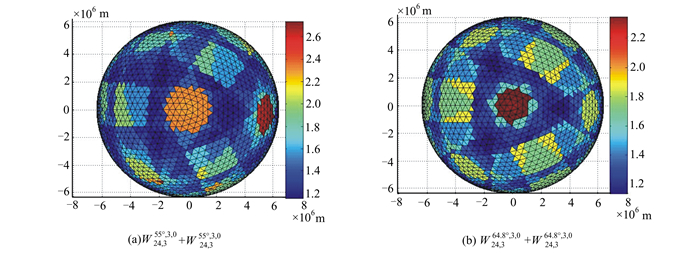
|
| 图 5 GLONASS星座二次设计 Fig. 5 Quadratic Optimization to GLONASS |
由于我国除海南、南海属于低纬度地区,大部分地区位于中纬度,因此,北斗MEO卫星采用55°轨道倾角的Walker构型和GEO混合星座具有现实意义。根据式(9),由于北斗星座引入了一定数目的GEO卫星,打破了55°倾角MEO卫星星座的最优性,可考虑与GLONASS星座进行组合改善全球地表GDOP分布(或根据式(9)调整MEO星座的轨道倾角)。根据星座的最优组合不变性[17],可通过组合GPS星座和GALLIEO星座,进一步改善系统在中高纬度地区的GDOP覆盖性能。
6 结 语(1) GPS卫星星座采用的轨道倾角非常接近单Walker构型的地心GDOP极值条件,但若所有GNSS轨道倾斜轨道倾角均采用54.74°,虽然多系统组合后的定位构型满足地心GDOP极值条件,但这并不满足多系统组合应用的地表均匀覆盖需求。对于新兴的GNSS星座,可采用本文给出的最小GDOP组合Walker构型,改善单一Walker构型的空间覆盖性能。
(2) GLONASS星座构型的轨道倾角采用64.8°,虽然该星座构型不满足地心GDOP极值条件,但在提高高纬地区的信号覆盖具有重要意义。在赤道轨道上引入一定数量的GEO卫星,可以改善GLONASS星座的全球地表GDOP分布,此外,通过引入由24颗卫星构成的轨道倾角为45.84°的Walker构型也可全面改善该星座的地表GDOP全球覆盖性能,该组合星座性能优于由48颗卫星构成的轨道倾角为54.74°的单一Walker构型。
(3) 在GNSS组合Walker星座设计中,使用式(9)将近似等价于地心GDOP极值约束、地表GDOP极值。
(4) 类似于导航卫星信号频率资源的国际分配机制,按照本文导出的条件方程分配和发展国家/区域单Walker构型,可确保组合Walker星座具有最佳定位精度。
(5) Walker星座的调相因子虽然不能改善地心GDOP,对在改善地表GDOP均值和方差方面具有一定的价值。
| [1] | Grafarend E W. Optimization of Geodetic Networks [J]. Boll Geod Sci Aff,1974, 33:351-406 |
| [2] | Schmitt G. Optimal Design of Geodetic Networks [J]. Deutche Geodatische Kommission, Munichen B, 1982, 258: 82-89 |
| [3] | Yang Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1): 1-6(杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010,39(1):1-6) |
| [4] | Yang Yuanxi. Some Notes on Uncertainty,Uncertainty Measure and Accuracy in Satellite Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5):646-650(杨元喜. 卫星导航的不确定性、不确定度与精度若干注记[J]. 测绘学报,2012,41(5):646-650) |
| [5] | Yang Yuanxi, Li Jinlong, Xu Junyi, et al. Contribution of the Compass Satellite Navigation System to Global PNT Users [J]. Chinese Science Bulletin, 2011, 56:2 813-2 819 |
| [6] | Kihara M, Okada T. A Satellite Selection Method and Precision for the Global Positioning System [J]. Navigation, 1984, 31:8-20 |
| [7] | Li Jianwen, Li Zuohu, Zhou Wei, et al. Study on the Minimum of GDOP in Satellite Navigation and Its Applications [J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(S1): 86-88(李建文, 李作虎, 周巍, 等. 卫星导航中几何精度衰减因子最小值分析及应用[J]. 测绘学报, 2011,40(S1): 86-88) |
| [8] | Deng Ping, Yu Lijian. GDOP Performance Analysis of Cellular Location System [J]. Journal of Southwest Jiaotong University,2005, 40(2):184-188(邓平, 余立建. 蜂窝定位系统GDOP性能分析[J]. 西南交通大学学报, 2005,40(2):184-188) |
| [9] | Feng Zunde, Lu Xiushan, Guo Ying. Diagnosis of Figure Advantage in Space Intersecting Model of Distance Measurement [J]. Bulletin of Surveying and Mapping, 2004, 12(1): 24-26(冯遵德, 卢秀山, 郭英. 测距空间交会测量模式中交会图形优劣的诊断[J]. 测绘通报, 2004,12(1): 24-26) |
| [10] | Li Deren. A Thought of Optimization and Design of Geodetic Networks in Consideration of Accuracy and Reliability[J]. Acta Geodaetica et Cartographica Sinica, 1989, 18(4): 241-248(李德仁. 顾及精度与可靠性的测量控制网优化设计的设想[J]. 测绘学报, 1989, 18(4): 241-248) |
| [11] | Li Deren, Zhou Yongqian. A Thought of Optimization and Design of Geodetic Networks in Consideration of Accuracy and Reliability[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1991,16(2):47-54(李德仁, 周勇前. 顾及精度与可靠性的测量控制网优化设计[J]. 武汉测绘科技大学学报, 1991,16(2):47-54) |
| [12] | Gao Yang. Optimal Design of Geodetic Networks Considering both Presicsion and Reliability Critera[J].Acta Geodaetica et Cartographica Sinica, 1987,16(3):232-239(高扬. 同时顾及精度和可靠性准则的控制网优化设计[J]. 测绘学报, 1987,16(3):232-239) |
| [13] | Zhang Zhenglu, Luo Nianxue, Huang Quanyi, et al. A New Method Based on Reliability of Engineering Control Network for Nets Optimization [J]. Geomatics and Information Science of Wuhan University, 2001,26(4):354-360(张正禄, 罗年学, 黄全义, 等. 一种基于可靠性的工程控制网优化设计新方法[J]. 武汉大学学报·信息科学版, 2001,26(4):354-360) |
| [14] | Xue Shuqiang. Matrix Volume and Its Applications in Network Design[D]. Beijing:Chinese Academy of Surveying and Mapping, 2007(薛树强. 矩阵体积及其在网形设计中的应用[D]. 北京:中国测绘科学研究院,2007) |
| [15] | Xue Shuqiang, Yang Yuanxi, Chen Wu, et al. Positioning Configuration with Minimum GDOP from Orthogonal Trigonometric Functions[J]. Geomatics and Information Science of Wuhan University, 2014, 39(7):820-825 (薛树强, 杨元喜, 陈武, 等. 正交三角函数导出的一类最小GDOP测距单点定位构型解集[J]. 武汉大学学报·信息科学版,2014,39(7):820-825) |
| [16] | Xue Shuqiang, Yang Yuanxi. Nested Cones of Single-point-Positioning Configuration with Minimal GDOP[J].Geomatics and Information Science of Wuhan University, 2014,39(11):1 369-1 374 (薛树强, 杨元喜. 最小GDOP测距单点定位构型的一种嵌套圆锥结构[J]. 武汉大学学报·信息科学版,2014,39(11):1 369-1 374) |
| [17] | Xue Shuqiang, Yang Yuanxi. Positioning Configurations with the Lowest GDOP and Their Classification[J]. Journal of Geodesy, 2015, 89(1): 49-71 |
| [18] | Xue Shuqiang, Yang Yuanxi, Dang Yamin, et al. Dynamic Positioning Configuration and Its First-order Optimization[J]. Journal of Geodesy, 2014, 88(2): 127-143 |
| [19] | Lannes A, Teunissen P J G. GNSS Algebraic Structures[J]. Journal of Geodesy, 2011, 85:273-290 |
| [20] | Walker J G. Satellite Constellations[J]. Journal of the British Interplanetary Society, 1984, 37: 559-571 |
| [21] | Yarlagadda R, Ali I, Al-Dhahir N, et al. GPS GDOP Metric[J]. IEE Proceedings—Radar, Sonar and Navigation, 2000, 147: 259-264 |
 2016, Vol. 41
2016, Vol. 41


