文章信息
- 丁国强, 马军霞, 熊明, 周卫东
- DING Guoqiang, MA Junxia, XIONG Ming, ZHOU Weidong
- SINS的SRC-KF姿态估计算法
- The SINS' SRC-KF Attitude Estimation Modeling Algorithm
- 武汉大学学报·信息科学版, 2016, 41(3): 367-372
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 367-372
- http://dx.doi.org/10.13203/j.whugis20140115
-
文章历史
- 收稿日期: 2014-02-17

2. 郑州轻工业学院软件学院, 河南 郑州, 450002;
3. 哈尔滨工程大学自动化学院, 黑龙江 哈尔滨, 150001
2. Software Engineering College, Zhengzhou University of Light Industry, Zhengzhou 450002, China;
3. College of Automation, Harbin Engineering University, Harbin 150001, China
姿态估计是载体姿态控制的关键问题,一般是通过载体捷联惯导系统(strap-down inertial navigation system,SINS)姿态模型和辅助观测信息利用高精度估计算法获得载体姿态估计结果,载体姿态估计精度会直接影响系统姿态、速度及位置量的计算精度。目前SINS姿态实时解算方法主要有旋转矢量法、欧拉法、四元数法以及修正罗德里格参数法等[1],其中四元数法应用最为广泛。但四元数必须进行归一化约束变换,该步骤限制了非线性滤波算法的应用。对此,Markley采用乘性扩展卡尔曼(MEKF)算法处理[2],但是MEKF算法高阶截断误差使其无法获得理想计算结果;Crassidis等提出了USQUE算法[3, 4]来避免四元数归一化约束。近年来,载体姿态的四元数卡尔曼滤波(quaternion Kalman filtering,QKF)算法获得得到广泛应用[5],QKF算法采用四元数伪观测模型,观测噪声与四元数向量是乘性关系,递推更新计算中四元数向量被强制归一化获得单位四元数向量。
目前针对非线性系统应用的采样逼近卡尔曼算法获得快速发展,主要有无迹卡尔曼滤波(unscented Kalman filter,UKF)算法[6]、中心差分滤波(central divided Kalman filter,CDKF)算法[7]以及类似的二阶插值滤波(SDDF)算法[8]和Gauss-Hermite滤波(GHKF)算法[9]等。GHKF算法复杂,计算负担重;UKF算法在高维场合应用中易于发散;CDKF和SDDF算法数值计算稳定性较差。设计高精度稳定数值计算的最优滤波算法成为载体姿态估计的关键问题,而基于球面径向容积积分逼近卡尔曼滤波算法的计算精度可以达到三阶[10, 11]以上,计算稳定性明显优于UKF与CDKF算法。
本文基于SINS姿态估计高精度和数值计算稳定性要求提出了一种SINS四元数姿态估计的球面径向容积卡尔曼(SRC-KF)模型算法,设计了新型四元数观测方程。姿态估计方程和观测方程具有相同的噪声项表达式。利用SINS/CCD姿态仿真平台开展模型算法验证研究。仿真结果表明了SINS的SRC-KF对准模型算法的有效性及计算优势。
1 SRC-KF非线性最优估计算法 1.1 球面径向容积逼近算法在高斯域内考虑函数F(X)数值积分:
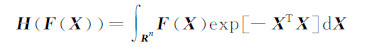
式中,n维状态向量X∈Rn,利用极坐标系中的方向向量Y和球径r表示X为X=rY,其中YTY=1,且有XTX=r2,r∈[0,∞),向量Y定义了单位超球面Un,则有:
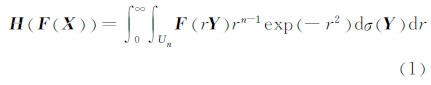
定义球面积分S(r)=∫UnF(rY)dσ(Y),重新整理式(1)为:
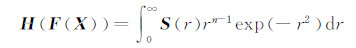
按照Gauss-Hermite数值积分,取ml个高斯求积点获得径向积分逼近计算:
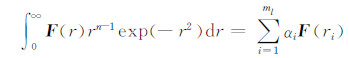
同样,取ms个求积点获得球面积分逼近:
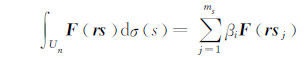
从而获得球面径向容积积分逼近计算:
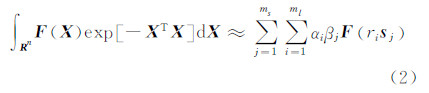
若取加权指数函数ω1(X)和概率密度分布加权函数ω2(X)有:ω1(X)=exp[-XTX],ω2(X)=N(X;η,Σ),且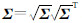 ,那么,有:
,那么,有:
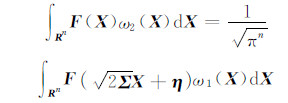
取ml=1,ms=2n,可获得三阶球面径向数值逼近计算:
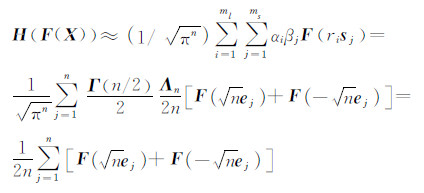
其中,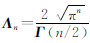 ,则2n个求积点为:
,则2n个求积点为:
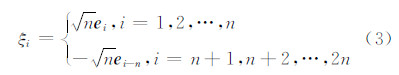
式中,ei表示第i列单位向量,其第i个元素为1,有容积逼近求积式:
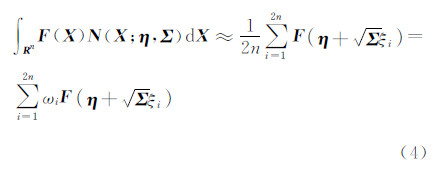
式中,ωi为权值系数,ωi=1/2n。
1.2 SRC-KF最优估计算法设计考虑非线性系统离散化模型方程:
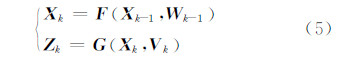
式中,Xk∈Rn和Zk∈Rm表示系统状态向量和量测向量;Wk和Vk是相互独立的过程噪声和观测噪声,具有Wk~N(0,Qk),Vk~N(0,Rk)分布。若观测向量序列Zk={Z1,Z2,…,Zk},系统状态向量和观测向量后验密度函数服从高斯分布。
若k时刻系统状态向量估计为Xk,估计方差矩阵为Pk,则对其实施乔里斯基分解:
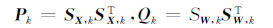
利用式(3)的求积点构造状态向量和过程噪声的采样点及其权值为:
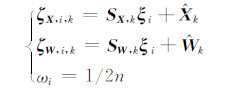
其中,i=1,2,…,2n。
那么{ζX,i,k;ζW,i,k}经由式(5)状态函数映射后获得的采样点更新值为:
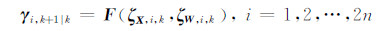
则系统状态向量的预测均值为:
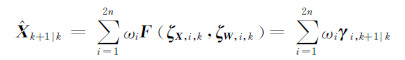
系统状态向量预测方差为:
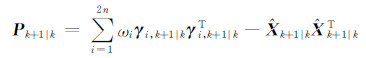
对系统状态向量预测方差和观测噪声方差矩阵同时展开乔里斯基分解,获得乔里斯基因子Pk+1|k=Sk+1|kSk+1|kT,Rk+1=SV,k+1|kSV,k+1|kT,则可以构造采样点为:
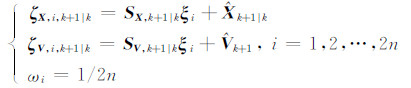
经由式(5)观测方程映射获得采样点更新值:
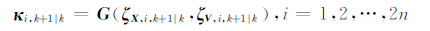
那么观测向量预测值为:
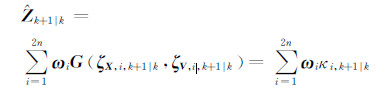
其预测方差矩阵为:
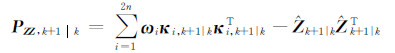
同时状态向量和观测向量交叉协方差为:
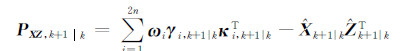
那么,由
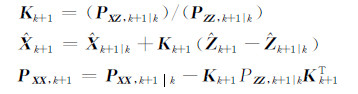
可以获得系统状态向量k+1时刻的估计值及其方差。
2 SINS姿态估计模型算法 2.1 SINS姿态方程四元数是表示载体姿态旋转的一类特殊四维矢量,定义四元数为Θ≡[ϑ0,ϑT]T,其中 =[ϑ1,ϑ2,ϑ3]T为向量分量,ϑ 0为实数分量,其运算要求必须满足规范化限制,即有:
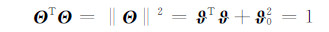
那么由四元数表示的姿态矩阵
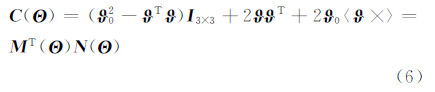
式中,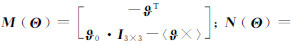
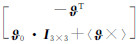 ;I3×3是单位矩阵;〈ϑ ×〉为斜对称矩阵[7]。
;I3×3是单位矩阵;〈ϑ ×〉为斜对称矩阵[7]。
根据四元数微分方程,结合式(6)进一步得到SINS系统姿态四元数微分方程:
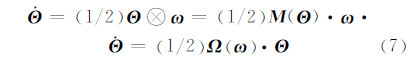
式中,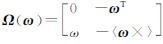 。
。
SINS系统姿态四元数微分方程中的角速率由载体坐标系中三轴速率陀螺测量得到,陀螺测量得到的角速率方程为:
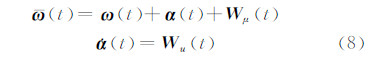
式中,ω(t)为陀螺量测输出角速率向量;α(t)为陀螺随时间的漂移量;Wμ(t)和Wu(t)分别为陀螺测量噪声和陀螺漂移的互不相关的高斯随机白噪声,满足Wu(t)~(0,ρμ2)和Wu(t)~(0,ρu2),从而SINS姿态四元数微分方程为:
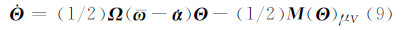
利用飞行器携带的辅助观测设备如星敏感器等可以获得精确的参考观测向量R,若在SINS载体系中得到的观测向量为B,那么由QUEST观测模型[12],有:
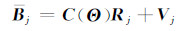
式中,Bj是一个具有观测噪声的3维观测向量;观测噪声Vj是观测传感器的误差向量,具有Vj~(0,ρB2)分布高斯白噪声。根据文献[5]可以得到SINS的伪观测模型方程:
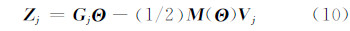
式中,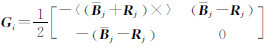 。则由式(10)展开k次观测获得的观测方程:
。则由式(10)展开k次观测获得的观测方程:
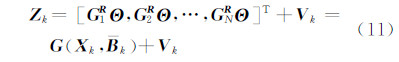
式中,G(Xk,Bk)=[G1RΘ,G2RΘ,…,GkRΘ]kT;Bk=[B1,B2,…,Bk]T。伪观测方程中的第一项GjΘ是四元数向量的线性函数,其矩阵秩[6]为2。伪观测方程中噪声项-M(Θ)Vj/2是四元数相关项,与四元数方程噪声项相似,可以方便开展观测噪声方差计算。
2.3 SINS模型噪声方差分解算法若考虑观测噪声与函数向量Xk相关的观测方程改为Zk=Ge(Xk)Vk,那么状态向量均值为[13]:
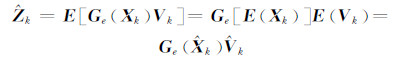
定义Zk外积计算式:
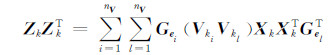
对其两边求期望值得到:
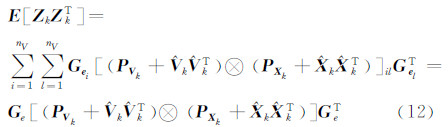
式中,Ge=[Ge1…GenV,式(12)可以简化为:
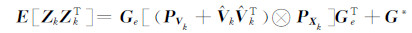
其中,G*=Ge[(PVk+VkVkT)ⓧXkXkT)]GeT,可简化为:
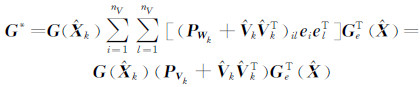
其中,ⓧ表示Kronecker乘积,且对于i=1,2,…,nV,有GeiXk=Ge(Xk)ei成立,从而可得到:
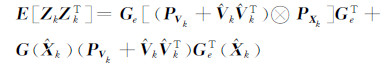
那么,向量Z的噪声方差为:
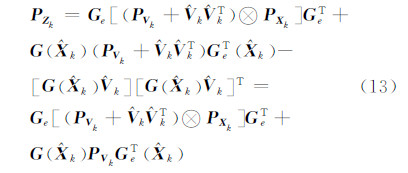
若噪声向量{Vk}是具有零均值高斯白噪声,则式(13)计算可以简化为:
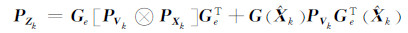
若四元数由k-1时刻到k时刻更新操作产生误差四元数为:
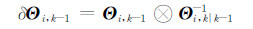
其中,Θi,k-1是k-1时刻更新计算的四元数,Θ i,k|k-1为四元数的一步预测值,那么δΘi,k-1向量部分δϑ i,k-1可表示为:
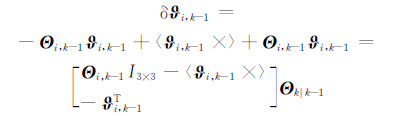
考虑SRC-KF算法中四元数均值计算加权系数,可以把四元数加权求均值问题转化为代价函数的极值计算问题,考虑四元数代价函数
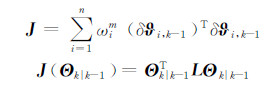
其中,
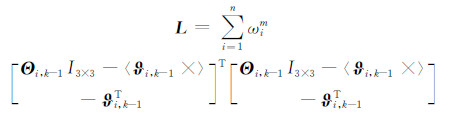
由于Θk|k-1TΘk|k-1=‖Θk|k-1‖=1,设拉格朗日算子λ,利用拉格朗日乘法构造代价函数[7]:
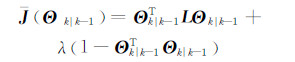
那么,可以通过计算函数最小值,得到:
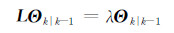
代价函数J最小矩阵L的最小特征值的特征向量就是所求均值四元数。
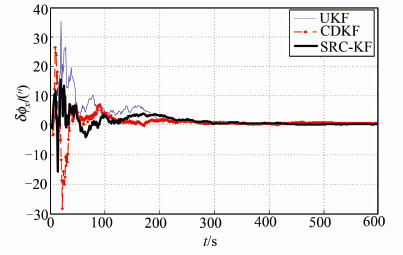
3 SINS系统模型仿真研究本文采用SINS/CCD姿态估计平台系统开展系统模型算法研究,光纤陀螺仪测量载体旋转角速度,利用两个光轴垂直安装的星敏感器获得星光矢量观测量。仿真初始条件设置为载体初始位置为北纬45°,东经126°,初始速度设为0,载体初始姿态角φx=2°,φy=4°,φz=15°,陀螺常值漂移为0.04°/h,随机漂移噪声设为0.005°/h1/2;星敏感器测量噪声为18″,系统仿真时间t=600 s。SRC-KF、CDKF、UKF算法同属于贝叶斯最优滤波算法,但由于采用不同的采样策略,为验证SINS姿态四元数SRC-KF模型算法的有效性及其数值计算比较的优势,本文针对系统模型开展3种算法对比仿真实验,从而获得SINS的图 1的纵摇姿态失准角估计误差δφx,图 2的横摇姿态失准角估计误差δφy数据和图 3的偏航失准角估计误差δφz数据以及表 1的估计误差数据。
|
| 图 1 纵摇角估计误差曲线 Fig. 1 Estimation Error Curves of Pitching Angle |
|
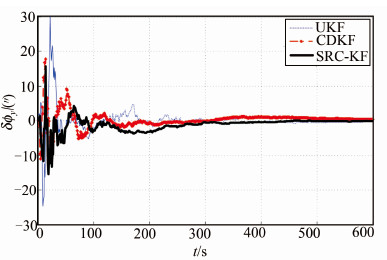
| 图 2 横摇角估计误差数据曲线 Fig. 2 Estimation Error Curves of the Rolling Angle |
|
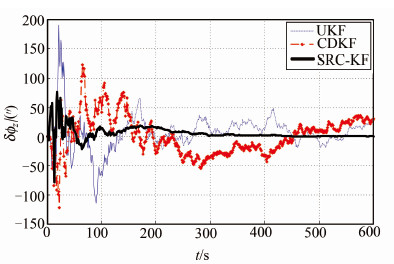
| 图 3 偏航角估计误差数据曲线 Fig. 3 Estimation Error Curves of Yawing Angle |
| 算法 | UKF | CDKF | SRC-KF |
| Δφx/(″) | 9.659 3 | 3.736 0 | 1.4571 |
| Δφy/(″) | 3.921 1 | 2.696 3 | 0.1895 |
| Δφz/(″) | -146.190 6 | 102.877 5 | -10.117 3 |
从仿真比较数据可以看出,SINS四元数姿态估计SRC-KF模型算法的计算精度明显优于CDKF和UKF算法计算精度,小角度的纵摇角和横摇角估计得到的图 1和图 2估计误差数据中SRC-KF算法估计精度在20″之内,而CDKF和UKF算法分别为25″和30″,相比于SRC-KF算法,CDKF和UKF算法的数值计算稳定性明显降低;同样在初始偏航失准角取值为15°情况下,SRC-KF算法计算精度优于其余两种算法,且SRC-KF算法数值收敛很快,稳定性也优于其余两种算法,这说明SRC-KF算法在姿态估计计算方面具有精度优势,原因在于SRC-KF算法采用球面径向容积法可以达到三阶计算精度,而CDKF算法的斯特林插值法和UKF算法的无迹变换法的计算精度仅能达到二阶。
另外,从表 1可以看出,SRC-KF算法的迭代时间小,CDKF算法收敛时间与其相近,UKF算法计算周期较长,原因在于SRC-KF和CDKF算法仅采用2n个采样点,而UKF算法需要2n+1个Sigma采样点,且SRC-KF和CDKF算法仅有一个采样点调整参数,而UKF算法需要3个参数调整采样点权值系数;同时系统两种噪声方差采用同样计算式展开计算,该措施也会影响到算法计算效率。
基于SINS姿态估计高精度稳定数值计算要求,利用球面径向积分数值逼近法设计计算精度达到三阶的SRC-KF算法,实现提高模型算法计算精度目的;利用四元数构建一类乘性噪声的SINS姿态四元数误差模型,系统方程中噪声与四元数状态向量具有乘性关系,利用噪声分离算法可用较小计算负担获得稳定计算性能。经由SINS/CCD姿态仿真平台验证,相比于CDKF和UKF算法,SINS SRC-KF姿态模型算法具有计算精度高且计算稳定特点,在飞行器载体SINS姿态估计应用中具有适用价值。
| [1] | Zhang Tianguang,Wang Xiuping, Wang Lixia. Strapdown Inertial Navigation Technology[M]. 2 nd ed Beijing:National Defense Industry Press, 2007: 287-367(张天光,王秀萍,王丽霞.捷联惯性导航技术(第二版)[M].第二版. 北京:国防工业出版社, 2007:287-367) |
| [2] | Markley F L.Attitude Error Representations for Kalman Filtering[J]. Journal of Guidance, Control, and Dynamics,2003,26(2): 311-317 |
| [3] | Crassidis J, Markley F. Attitude Estimation or Quaternion Estimation [J]. Journal of the Astronautical Sciences,2004,52(2): 221-238 |
| [4] | Shuster M D. Filter Quest or Request[J]. Journal of Guidance, Control, and Dynamics, 2009,32(2):643-645 |
| [5] | Choukroun D, Bar-Itzhack I Y, Oshman Y. Novel Quaternion Kalman Filter [J]. IEEE Transaction on Aerospace and Electronic Systems, 2006,42(1):174-190 |
| [6] | Halil E S, Chingiz H. Pico Satellite Attitude Estimation via Robust Unscented Kalman Filter in the Presence of Measurement Faults [J]. ISA Transactions, 2010, 49(3):249-256 |
| [7] | Ding Guoqing, Zhou Weidong, Hao Yanling. QCDKF Algorithm for a Transfer Alignment System by Using Multiplicative Quaternion Error Model [J]. J Huazhong Univ of Sci& Tech(Natural Science Edition), 2010,38(8):89-94(丁国强,周卫东,郝燕玲. 传递对准误差模型及其QCDKF算法[J].华中科技大学学报(自然科学版),2010,38(8): 89-94) |
| [8] | Ding Guoqiang, Zhou Weidong, Hao Yanling. Study on Divided Difference Filtering and Its Application on Large Initial Misalignment Transfer Alignment Sytem [J]. Journal of Projectiles,Rockets,Missiles and Guidance, 2010,30(4):163-168(丁国强,周卫东,郝燕玲. 插值非线性滤波技术在大失准角传递对准中的应用研究[J]. 弹箭与制导学报,2010,30(4):163-168) |
| [9] | Gao F Q, Chen L R, Ding C H. Simplified Gauss Hermite Filter Based on Sparse Grid Gauss Hermite Quadrature [J]. Telkomnika, 2013, 11(12):7 138-7 145 |
| [10] | Lasserre J B.The Existence of Gaussian Cubature Formulas [J]. Journal of Approximation Theory, 2012, 164(5):572-585 |
| [11] | Bin J, Ming X, Yang C. High-Degree Cubature Kalman Filter [J]. Automatica, 2013,49(2):510-518 |
| [12] | Angelo M, Oshman S. Quaternion -Based Extended Kalman Filter for Determining Orientation by Inertial and Magnetic Sensing [J]. IEEE Transactions on Biomedical Engineering, 2006,53(7): 1 346-1 356 |
| [13] | Liu Zhiping, Zhang Shubi.Variance-covariance Component Estimation Method Based on Generalization Adjustment Factor [J]. Geomatics and Information Science of Wuhan University, 2013, 38(8):925-929(刘志平,张书毕.方差-协方差分量估计的概括平差因子法[J].武汉大学学报·信息科学版,2013,38(8):925-929) |
 2016, Vol. 41
2016, Vol. 41


