文章信息
- 李桢, 黄劲松
- LI Zhen, HUANG Jingsong
- 基于RSSI抗差滤波的WiFi定位
- WiFi Positioning Using Robust Filtering with RSSI
- 武汉大学学报·信息科学版, 2016, 41(3): 361-366
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 361-366
- http://dx.doi.org/10.13203/j.whugis20130801
-
文章历史
- 收稿日期: 2014-12-04

2. 地球空间信息技术协同创新中心, 湖北 武汉, 430079
2. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China
WiFi定位是目前室内定位的主要技术方法,其观测值主要为接收信号强度(received signal strength indication,RSSI)。利用RSSI定位一般有以下两类方法:① 利用信号传播模型将RSSI转换为距离,进行距离交会;② 利用事先采集的信号强度背景场进行空间匹配。其定位精度都依赖于稳定可靠的信号强度值。由于室内环境复杂多变,信号衰减严重,使得RSSI不稳定,滤波是解决该问题的方法之一。
根据处理的对象不同,滤波可分为以下两类:① 对定位坐标进行滤波。如香港理工大学Chan等[1]利用K邻近法进行位置估计,然后对已估计出的位置进行卡尔曼滤波,从而达到平滑去噪的目的。② 直接对RSSI进行滤波,如Youssef等采用离线采集的信号强度进行内插,然后用卡尔曼滤波方法估计位置[2]。
本文对室内环境WiFi信号衰减规律及RSSI统计特性进行了研究,采用抗差卡尔曼滤波方法对RSSI进行滤波并同时估计距离。利用滤波后的观测量进行定位的结果表明,本文方法可明显提高定位精度。
1 信号强度衰减规律及特征 1.1 WiFi信号距离衰减模型WiFi信号工作在2.4 GHz频段,自由空间中,接收设备的接收功率由Friis传输方程[3]给出:
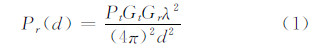
式中,Pr为接收功率;Pt为发射功率;Gt为发射天线增益;Gr为接收天线增益;λ为发射信号的波长;d为收发天线之间的距离。如果选取距离d0作为参考,则有:

为了方便计算,一般将功率转换为以dB为单位,以1 mw作为参考,其相应的单位为dBm,其转换公式为:
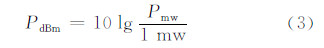
对式(2)进行单位转换,可以得到传统的距离衰减模型:
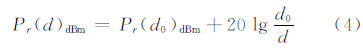
但是由于室内环境复杂多变,导致实际所测信号的强度并不满足以上的规律。为了比较灵活地适应建筑物及阻挡物对信号强度的影响,文献[3]中提出信号强度的衰减因子模型:
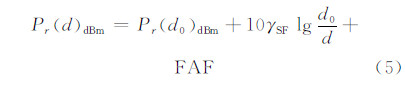
式中,γSF表示同层测试的路径损耗指数值;FAF表示附加衰减因子。
本文对某AP取d0=1 m,Pr(d0)=-29 dBm,分别对Friis传输方程和信号衰减因子模型进行了对比,结果如图 1所示,在该实验环境中,利用实测数据估计式(5)中的参数(衰减因子γSF和路径损耗指数FAF)得:FAF=-1.076;γSF=2.275(不同实验环境中所得到的值稍有不同);其标准差为1.59 dBm。在距离较近时,衰减因子模型、Friis传输方程的计算结果都较接近实测值,但随着距离的增加,Friis传输方程的计算值与实测值相差较大,而衰减因子模型则具有更好的适应性。图 2为衰减因子模型与实测值的差异。

|
| 图 1 衰减曲线拟合结果 Fig. 1 The Fitting Curve of Attenuation Factor Model |

|
| 图 2 实测信号强度和衰减因子模型差值 Fig. 2 Difference of RSSI Between the Measured and Attenuation Factor Model |
衰减因子模型由于受到环境中各种因素的影响而与实际不符,因此,有必要分析实际环境中RSSI的统计特性。文献[4]对走廊和房间内WiFi信号强度的偏度进行了分析,发现信号强度具有左偏特性,不能用高斯分布来简化,他们的研究表明,采用对数衰减模型进行参数拟合后,在18 m范围内,可使测距精度达到3 m。
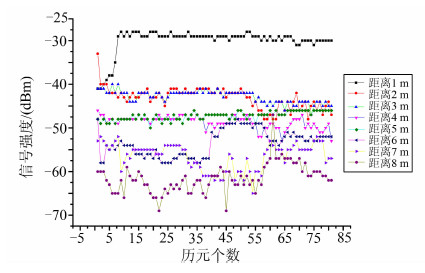
为了研究信号强度的统计特性,本文在室内对某个AP不同距离的RSSI进行了连续观测,得到不同距离RSSI时间序列如图 3所示。
|
| 图 3 不同距离信号强度时间序列(静态) Fig. 3 RSSI Time Sequence with Different Distances(Static) |
图 3表明在短距离(一般小于3 m),由于信号强度比较强,不易受到外界环境的干扰。而当距离大于6 m,信号强度本身比较弱,较易受到外界环境影响,波动幅度也较大,信号强度的较大波动降低了WiFi定位精度。
本文主要从均值μ、方差σ2、偏度α (式(6))和峰度β(式(7))等统计量的角度对数据进行了分析,结果如表 1所示。
| 距离/m | 均值 | 方差 | 偏度 | 峰度 |
| 1 | -29.87 | 1.07 | -3.49 | 17.56 |
| 2 | -44.25 | 1.87 | 0.52 | 4.86 |
| 3 | -44.03 | 1.45 | -0.36 | 2.54 |
| 4 | -48.67 | 1.09 | -1.02 | 4.09 |
| 5 | -45.94 | 0.74 | -0.19 | 3.31 |
| 6 | -51.48 | 2.18 | 0.08 | 2.28 |
| 7 | -55.21 | 2.11 | -0.61 | 2.98 |
| 8 | -59.97 | 2.33 | 0.67 | 6.40 |

表 1表明,8 m以内的信号强度偏度值大部分表现出左偏特性,信号强度分布表现为长尾,这与文献[4]的实验结论一致。本文还计算了信号强度的方差与距离的相关系数为0.578;表明信号强度的采集精度不会随着距离的增加而降低(但是由于距离与RSSI之间的对数关系,不敏感的信号强度导致较大距离误差)。由于正态分布的峰度值为3,而本文所得峰度值表明RSSI不符合正态分布。
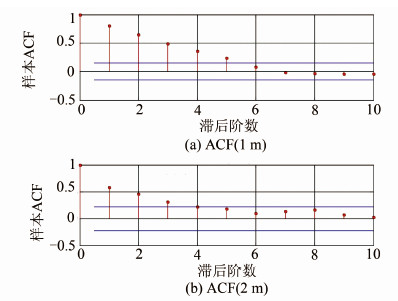
本文对不同距离所采集的信号强度值进行了自相关分析。图 4只给出2 m内信号强度值自相关系数,表明滞后8阶自相关系数将小于0.2。在信号强度采集过程中,为了得到较为真实的信号强度值,一般采取多次测量后取平均值的方式,该统计结果表明同一个点的测量次数应大于8。
|
| 图 4 不同距离自相关系数图(2 m内) Fig. 4 Autocorrelation Coefficient Map with Different Distances(Within 2 m) |
在信号强度的采集过程中,RSSI可能出现粗差,因此,在滤波器的构建中必须要处理好信号强度中的粗差。基于对RSSI的统计分析,本文采用抗差M估计方法进行信号强度的卡尔曼滤波。估计的准则是寻找一个非负的凸标量函数,使得:
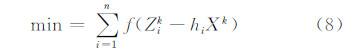
式中,Zik 表示时刻k观测向量中第i个元素,观测向量的维数是n;hi表示观测矩阵H的第i行,hi=(hi1,hi2,hi3,…,him);m是待估向量的维数。为了求得式(8)的最小值,令e(k)i=Zik -hiXk,对Xk求导并令其为0,可得:
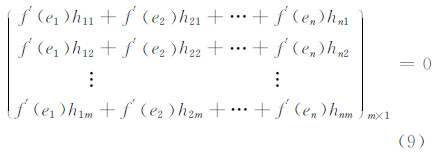
式(9)又可以写成:

式中,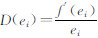 。
。
式(10)写成矩阵形式为:

式中,Dk=diag[D(e1),D(e2),…,D(en)]。
利用M估计对卡尔曼滤波进行解算,偏差大的测量值主要是通过新息来影响滤波结果,因此,在出现粗差时,应采取适当的方法来对新息进行修正,可在一定程度上减小粗差对估计值的影响。新息中的粗差通过增益矩阵Kk影响状态滤波值,根据新息来调节增益矩阵Kk可以削弱或消除粗差的影响[5]。调整后的增益矩阵为:

式中,D即为等价权函数。
其卡尔曼滤波的递推公式为:

一般对于具有左偏特性的分布,类似于IGG方案[6, 7],其等价权函数D(ek)为:
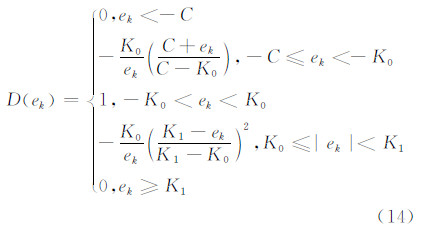
式中,K0、K1、C可根据经验选取,一般选取K0为1.0~1.5;K1可以有较大的变动,对于具有较强几何检核的系统,K1可以选较小数值。一般地,为了顾及非对称分布,C的取值要比K1大。
分析式(14),本文在合理假设的前提下尝试寻找K0、K1、C与观测值之间的关系,从而达到参数K0、K1、C自适应的目的。以上参数表征了观测残差的某一范围,根据经验,本文选取残差的两倍中误差为K0;选取残差的3倍中误差为K1和C。
本文采用Friis传输方程作为RSSI滤波的系统状态方程,选取距离、速度和RSSI作为系统状态空间。系统的观测方程中只有信号强度的观测值。由于WiFi采样时间间隔比较短,则在短时间内,用户的运动可以近似地用匀加速度运动来描述。滤波系统的状态方程可以表述为:
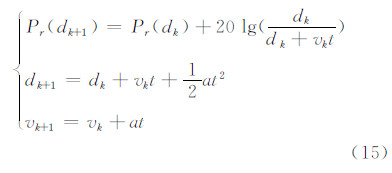
式中,d表示用户当前位置距离某AP的距离;t表示采样间隔;a表示采样间隔时间内用户的运动加速度;v表示用户当前运动速度,其方向为用户远离AP时为正,靠近AP时取值为负。
由于本文所用的WiFi的测量值只有RSSI,若用户设备的信号强度测量误差为r,易得该系统的观测方程为:
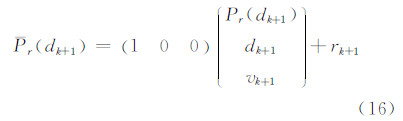
滤波系统经过线性化后的状态转移矩阵为:

式中,dk0 、vk0 表示k时刻的状态概略值。
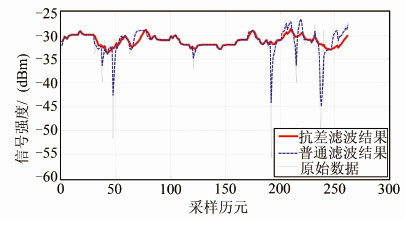
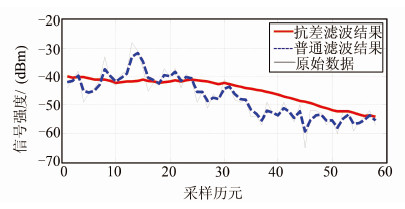
3 信号强度滤波实例分析为了对比抗差滤波和普通滤波的效果,本文分别在静态情形下和动态场景中对所采集的RSSI进行了处理,如图 5和图 6所示。当环境发生变化时,信号强度值的波动较大,如图 5中的历元50、190和240附近。试验结果表明,无论是在静态还是动态情形下,基于M估计的抗差滤波都比普通滤波更能适应环境变化,且能取得较好的信号平滑效果。
|
| 图 5 RSSI滤波效果对比(静态) Fig. 5 Comparison of RSSI Filtering Effect(Static) |
|
| 图 6 RSSI滤波效果对比(动态) Fig. 6 Comparison of Distance Filtering Effect(Dynamic) |
为了进一步验证信号强度抗差滤波的定位效果,基于距离交会进行了定位实验。本定位实验场面积为10 m×9 m,实验场景见图 7。在室内布设4个AP,按照距离交会定位需要对各个AP按照距离衰减因子模型进行标定,各AP标定结果如表 2。
| AP名 | X | Y | γSF | FAF | 1 m处RSSI |
| AP1 | 9.0 | 7.8 | 2.556 | 0.647 | -27 |
| AP2 | 0.0 | 0.6 | 2.275 | -1.076 | -30 |
| AP3 | 9.0 | 1.8 | 2.970 | 0.572 | -21 |
| AP4 | -1.2 | 7.8 | 2.751 8 | 1.314 7 | -28 |

|
| 图 7 实验场景及实验用AP Fig. 7 The Scene and AP Used in Experiment |
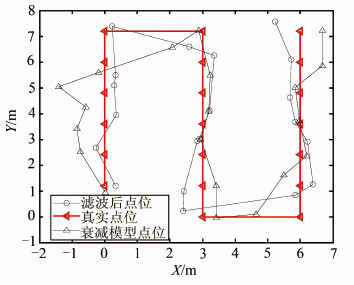
本文分别进行了动态和静态的定位实验。在静态定位中,选取了20个参考点,其坐标精确已知。在这20个点上进行了多次测量,分别用抗差滤波方法和距离衰减因子模型进行处理,得到定位结果点位(多次测量平均值)如图 8。表 3为定位结果与已知坐标的差值。
|
| 图 8 抗差滤波、衰减模型和真实点位 Fig. 8 The Points of Robust Filtering, Attenuation Factor Model and the Original |
| /m | ||||||
| 点号 | 抗差滤波偏差 | 衰减模型偏差 | ||||
| dX | dY | 点位RMS | dX | dY | 点位RMS | |
| 1 | -0.34 | 0.0 | 0.38 | -0.02 | 0.27 | 0.25 |
| 2 | 0.28 | -0.28 | 0.42 | 0.76 | -0.11 | 0.81 |
| 3 | -0.36 | -0.34 | 0.47 | 0.85 | 0.20 | 0.84 |
| 4 | -0.29 | -0.30 | 0.41 | 0.585 | 0.54 | 0.78 |
| 5 | -0.33 | 0.5 | 0.56 | 1.41 | 0.96 | 1.8 |
| 6 | -0.22 | -0.18 | 0.31 | 0.18 | 1.61 | 1.62 |
| 7 | 0.40 | 0.62 | 0.75 | 0.92 | 0.62 | 1.20 |
| 8 | -0.35 | -0.24 | 0.39 | 0.12 | -1.22 | 1.31 |
| 9 | -0.22 | 0.69 | 0.74 | -0.23 | -0.68 | 0.68 |
| 10 | 0.08 | 0.58 | 0.56 | -0.19 | -0.48 | 0.53 |
| 11 | 0.16 | -0.52 | 0.48 | 0.05 | -0.62 | 0.64 |
| 12 | 0.58 | 0.21 | 0.63 | -0.42 | 0.01 | 0.39 |
| 13 | 0.59 | -0.21 | 0.59 | -0.43 | 0.03 | 0.45 |
| 14 | 0.15 | -0.82 | 0.85 | 1.36 | -0.10 | 1.37 |
| 15 | -0.38 | -0.05 | 0.36 | 0.50 | -0.43 | 0.67 |
| 16 | -0.23 | -0.50 | 0.58 | -0.21 | 0.04 | 0.23 |
| 17 | 0.16 | -0.08 | 0.21 | 0.03 | -0.11 | 0.12 |
| 18 | 0.33 | 0.19 | 0.37 | 0.15 | -0.20 | 0.31 |
| 19 | 0.27 | -0.10 | 0.25 | -0.68 | 0.14 | 0.71 |
| 20 | 0.77 | -0.38 | 0.86 | -0.69 | -0.04 | 0.68 |
通过对多次观测的信号强度值进行滤波可以有效地剔除观测值中的噪声。从表 3可以看出,在通过滤波得到稳定信号强度的基础上,采用信号强度距离交会平均点位误差为0.544 m;X方向的均方根误差为0.363 m;Y方向的均方根误差为0.406 m,而直接采用距离衰减因子模型进行交会平均点位误差为0.871 m;X方向的均方根误差为0.636 m,Y方向的均方根误差为0.598 m。在静态情形下,通过对RSSI进行滤波处理可以提高定位精度。
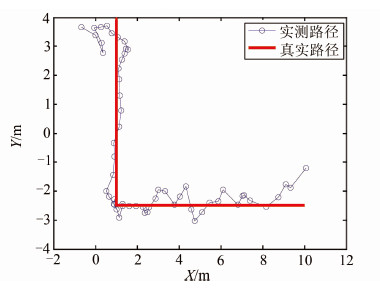
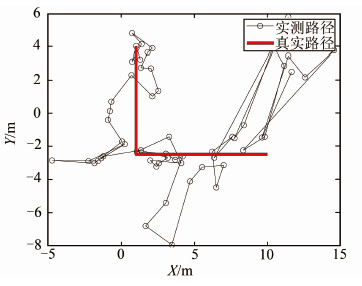
在动态情形下,各定位AP信息与静态情形一致,如表 2。手持设备以人步行速度移动,进行实时滤波和定位处理。抗差滤波定位结果和衰减因子模型定位结果分别如图 9和图 10。抗差滤波算法所有历元定位的平均点位中误差为1.406 m;而衰减因子模型所有历元定位的平均点位中误差为5.383 m。
|
| 图 9 抗差滤波处理后的路径 Fig. 9 The Path with Robust Filter |
|
| 图 10 无滤波处理的路径 Fig. 10 The Path Without Filter |
图 9、图 10表明,动态情形下采用本文的抗差滤波算法仍能获得较好的定位效果,而采用原始信号进行距离交会定位则表现为噪声状态,几乎将真实的路径淹没了。
4 结 语本文首先探讨了信号强度的衰减规律及其统计特性,根据其左偏特性,选取相适应的影响函数。在抗差滤波中利用影响函数对增益矩阵进行修正达到了抗差的效果。
本文的实验表明,与距离衰减因子模型相比,无论静态还是动态情形,抗差滤波方法明显好于距离衰减因子模型,采用抗差滤波算法可以为WiFi定位提供较平滑的信号强度,从而提高WiFi定位精度。
| [1] | Chan E C L, George B, Mak S C. Using WiFi Signal Strength to Localize in Wireless Sensor Networks[C]. The WRI International Conference on Communications and Mobile Computing, Yunnan,China, 2009 |
| [2] | Seifeldin M A,El-keyi A F, Youssef M A. Kalman Filter-based Tracking of a Device-free Passive Entity in Wireless Environments[C].The 6th ACM International Workshop on Wireless Network Testbeds, Experimental Evaluation and Characterization, New York, USA, 2011 |
| [3] | Wan Qun, Guo Xiansheng, Chen Zhangxin.The Principle and Application of Indoor Localization[M].Beijing: Electronic Industry Press,2012:80-81(万群,郭贤生,陈章鑫.室内定位理论、方法和应用[M].北京:电子工业出版社,2012:80-81) |
| [4] | Jiang Li,Xie Yongping.Research on Indoor Ranging based on WiFi[OL]. China Sciencepaper Online, http://www.paper.edu.cn/releasepaper/content/201005-262,2010-05-14(姜莉,解永平.基于WiFi的室内测距研究[OL].中国科技论文在线,http://www.paper.edu.cn/releasepaper/content/201005-262,2010-05-14) |
| [5] | Wang Jian, Wang Jinling,Gao Jinxiang. Research on GNSS Navigation Model Based on Robust EKF[J]. Journal of China University of Ming & Technology, 2008,37(4):473-477 (王坚,王金岭,高井祥. 基于抗差EKF的GNSS导航模型研究[J]. 中国矿业大学学报,2008,37(4):473-477 ) |
| [6] | Yang Yuanxi. The Estimation of Adaptive Least Square[J]. Acta Geodaetica et Cartographica Sinica,1996,25(3):206-211(杨元喜. 自适应抗差最小二乘估计[J]. 测绘学报,1996,25(3):206-211) |
| [7] | Zhang Shuangcheng, Yang Yuanxi, Zhang Qin. An Algorithm of GPS Navigation Based on Robust Self-Tuning Kalman Filtering[J]. Geomatics and Information Science of Wuhan University, 2005,30(10):881-884(张双成, 杨元喜, 张勤.一种基于抗差自校正Kalman滤波的GPS导航算法[J]. 武汉大学学报·信息科学版, 2005, 30(10):881-884) |
 2016, Vol. 41
2016, Vol. 41


