文章信息
- 汪奇生, 杨德宏, 杨腾飞
- WANG Qisheng, YANG Dehong, YANG Tengfei
- EIV模型参数估计的新方法
- A New Method of Parameter Estimation for the EIV Model
- 武汉大学学报·信息科学版, 2016, 41(3): 356-360
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 356-360
- http://dx.doi.org/10.13203/j.whugis20140182
-
文章历史
- 收稿日期: 2014-06-17

2. 湖南软件职业学院, 湖南 湘潭, 411100
2. Hunan Software Vocational Institute, Xiangtan 411100, China
总体最小二乘(TLS)自从被Golub提出以来[1],在各个领域都得到了广泛的应用。由于其能顾及系数矩阵的误差,在理论上较最小二乘(LS)严密。对于测量数据处理中系数矩阵含有误差的总体最小二乘问题,通常需要建立相应的EIV( errors-in-variables)模型来进行参数估计。关于EIV模型参数估计的算法,相关学者进行了一些研究。其中包括将观测值和系数矩阵元素看成是独立等精度的总体最小二乘算法(包括混合总体最小二乘LS-TLS)[2, 3, 4, 5] ;将观测值和系数矩阵元素看成是独立但不等精度的加权总体最小二乘(WTLS)[6, 7, 8, 9];顾及系数矩阵重复元素或考虑系数矩阵结构性质的结构总体最小二乘(包括混合结构总体最小二乘)(STLS)[10, 11]以及其他的扩展算法[12]。近年来,EIV模型参数估计的算法在理论上已经取得了许多成果,但对于简化EIV模型参数估计的算法以及确定其精度评定公式将是总体最小二乘研究的重要目标[12]。鉴于此,本文根据非线性最小二乘平差理论并用结构矩阵来顾及系数矩阵的重复元素,提出了一种EIV模型参数估计的新方法,并给出了精度评定公式。同时,新方法将总体最小二乘、加权总体最小二乘以及结构总体最小二乘等3种算法统一起来,而且算法的推导过程及其迭代格式较为简单。最后通过算例进行了具体分析,结果验证了本文方法的有效性和可行性。
1 EIV模型及其估计新方法 1.1 总体最小二乘平差模型(EIV模型)总体最小二乘平差模型(EIV模型):
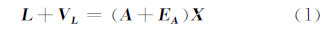
式中,L为m×1的观测向量;VL为m×1的观测值改正向量;A为m×n的系数矩阵;EA为m×n的系数改正矩阵;X为n×1的参数估值向量。其随机模型为:
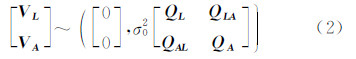
式中,VA=vec(EA)为mn×1的向量,vec(EA)即将矩阵EA从左至右逐列拉直成mn×1的向量;σ02为单位权方差;QL为m阶观测值的协因数阵;QA为mn阶的系数矩阵元素的协因数阵;QLA为m×mn的观测值与系数矩阵元素的互协因数阵,且QLA=QALT。其估计准则为:

从式(1)可以看出,由于EIV模型考虑了系数矩阵的误差,其平差模型很难直接求解。特别是在加权情况下,目前在测量数据处理领域的求解方法基本都是采用迭代方法。
1.2 EIV模型参数估计的新方法由于总体最小二乘属于非线性估计[12],根据文献[8]对EIV模型进行线性化,然后逐次迭代求解,则可将式(1)在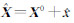 处展开可得:
处展开可得:

式中,EAX0=((X0)TⓧIm×n)VA=FVA,其中ⓧ为矩阵的克罗内克积。在测量数据处理中,一些平差模型的系数矩阵并不是所有元素都含有误差,甚至有些元素是有常数项组成,这就在VA中产生许多不需要改正的元素(改正数为0)。因此,可将系数矩阵的改正向量用结构矩阵来表示:

式中,VA是t×1的系数矩阵中含误差的非重复的元素的改正数(数量为t个);D是mn×t的结构矩阵。由此,可将式(4)进一步表示为:
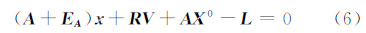
式中,R=[-Im FD]为m×(m+t)的矩阵; V=[VL VA]T为(m+t)×1的改正向量;Im为m阶单位矩阵。在考虑观测值与系数矩阵元素独立(不相关)不等精度时,则此时EIV模型的随机模型为:

式中,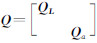 为(m+t)阶的协因数阵;Qa为t阶的系数矩阵含误差非重复元素的协因数阵。则总体最小二乘平差准则为:
为(m+t)阶的协因数阵;Qa为t阶的系数矩阵含误差非重复元素的协因数阵。则总体最小二乘平差准则为:

根据平差准则可构造目标函数:

式中,k为m×1的拉格朗日常数向量。
根据拉格朗日求极值原理,要使式(9)求得最小值,则φ关于V和x的偏导要等于零,即有
:
将式(10)化简整理可得:

根据式(11)再结合式(6)可得:
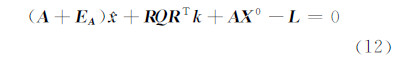
根据式(12)、式(11)的第二式,则有:

式中,i为迭代第i步。EIV模型的总体最小二乘解便可通过上述方程组逐步迭代求得,即根据给定的初值EA(0) 和X0(0),可以求解式(12),得到待求参数x1和拉格朗日常数k1以及误差向量V,将更新得到的EA和X0作为新的初值代入式(13)重新计算,直到满足收敛条件为止。
通过上述推导,根据式(13)的迭代格式,可以将EIV模型参数的总体最小二乘估计几种常见算法统一起来。
1) 总体最小二乘(包括混合总体最小二乘)。如果观测值和系数矩阵元素独立等精度则权阵为单位矩阵,可以通过式(13)进行迭代。如果系数矩阵还存在常数项,则只需构造结构矩阵D来进行计算。
2) 加权总体最小二乘。如果观测值和系数矩阵元素独立但不等精度,则按式(13)的迭代格式进行解算即可。
3) 结构总体最小二乘(包括混合结构总体最小二乘)。如果系数矩阵的元素存在明显的规律性或含有重复元素,则只需构造其相应的结构矩阵便可通过式(13)进行迭代计算。
由此,EIV模型参数估计新方法的具体解算步骤如下。
1) 给参数赋初值X0(0)(一般选取最小二乘解为初值),根据算法的类型构造结构矩阵D(如是总体最小二乘则不需构造结构矩阵),设EA(0)=0由参数的初值X0(0)加上结构矩阵D构造R(0)。
2) 根据式(13)计算x和k,并根据X0(i+1)=X0(i)+x(i+1)V(i+1)=QR(i)Tk(i+1)EA(i+1) =vec-1(VA(i+1) )计算新的迭代值,其中vec-1(·)表示vec(·)的逆运算,即将mn×1的列向量重新构造成m×n的矩阵。
3) 根据新值重复步骤2),直到|x(i+1)|<ε,通常取ε=10-10。
1.3 精度评定单位权中误差评定公式为:
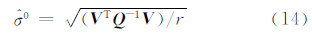
式中,V=QRTk;r为自由度,在测量数据处理中自由度可以理解为多余观测量,在总体最小二乘的EIV模型中,观测值除了原观测向量还包括系数矩阵含误差的值,本文为(m+t)个,必要观测数(即待估参数)除了原有参数也要包括系数矩阵含误差的元素,因为只有得到原参数和系数矩阵元素的改正数,才能进行迭代运算的参数更新,进而才能对式(13)进行解算,因此,必要观测数为(n+t),r=(m+t)-(n+t)。总体最小二乘的自由度与最小二乘相同,这与文献[7, 8]的结论是一致的。由式(13)根据方块矩阵求逆,可得到迭代到最后一步时,参数改正数的表达式:
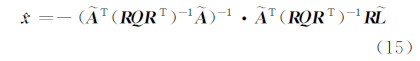
式中,Ã为改正后的观测矩阵;R =[-Im FD]·[L hA]T,QLL=Q,Ã=A+E,D·hA=vec(A),hA是t×1的系数矩阵中含误差的非重复的元素。根据协因数传播定律,可得:
=[-Im FD]·[L hA]T,QLL=Q,Ã=A+E,D·hA=vec(A),hA是t×1的系数矩阵中含误差的非重复的元素。根据协因数传播定律,可得:
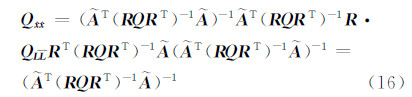
则参数精度评定公式为:

为了验证本文方法能对结构总体最小二乘进行解算,采用一个坐标转换的算例来进行分析,其三维坐标观测值如表 1所示,由于三维坐标转换模型的系数矩阵不但含有常数列,而且其他列还含有重复元素和常数项,很显然这是一个混合结构总体最小二乘[11]。要求解三维坐标转换的总体最小二乘解,既要考虑系数矩阵的误差,又要顾及系数矩阵的重复元素。而混合总体最小二乘只能顾及系数矩阵的前三列常数列,对后四列的重复元素和常数元素无法顾及,所以要求解最优解一般是采用加权总体最小二乘法[6]。即对系数矩阵的每个元素赋予权重来进行求解,这样的处理方法虽然能求得参数的解,但构造权阵时较为麻烦。而本文方法可以用来解决这样的混合总体最小二乘,即先构造结构矩阵,其构造方法如下:
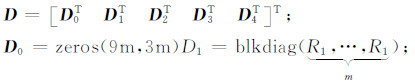

| 点号 | 原始坐标/m | 目标坐标/m | ||||
| X | Y | Z | X | Y | Z | |
| 1 | -2 802 191.348 2 | 5 009 064.765 7 | 2 772 381.176 8 | -2 802 088.418 2 | 5 009 123.156 9 | 2 772 386.569 9 |
| 2 | -2 810 175.651 5 | 5 016 086.112 0 | 2 751 955.053 1 | -2 810 072.730 9 | 5 016 144.572 1 | 2 751 960.500 7 |
| 3 | -2 820 567.227 2 | 5 009 905.344 4 | 2 752 470.385 8 | -2 820 464.394 2 | 5 009 963.991 7 | 2 752 475.921 1 |
| 4 | -2 817 162.653 8 | 5 002 454.352 0 | 2 769 299.110 6 | -2 817 059.835 1 | 5 002 512.999 3 | 2 769 304.628 8 |
| 5 | -2 825 775.818 2 | 4 995 785.495 5 | 2 772 390.169 5 | -2 825 673.090 6 | 4 995 844.301 3 | 2 772 395.762 9 |
| 6 | -2 821 096.763 4 | 4 981 344.211 2 | 2 802 869.494 4 | -2 820 994.060 5 | 4 981 403.048 6 | 2 802 875.077 3 |
| 7 | -2 824 710.665 4 | 4 984 669.284 6 | 2 793 431.999 9 | -2 824 607.984 6 | 4 984 728.145 8 | 2 793 437.599 7 |
| 8 | -2 827 287.538 0 | 4 983 602.697 4 | 2 792 671.081 7 | -2 827 184.875 9 | 4 983 661.601 6 | 2 792 676.704 2 |
| 9 | -2 759 256.958 4 | 5 019 419.072 5 | 2 796 705.276 2 | -2 759 153.720 2 | 5 019 476.803 6 | 2 796 710.316 7 |
| 10 | -2 800 063.333 9 | 5 001 135.290 0 | 2 788 830.195 9 | -2 799 960.417 6 | 5 001 193.709 4 | 2 788 835.580 2 |
| 11 | -2 841 162.870 7 | 4 981 982.504 1 | 2 781 464.448 9 | -2 841 060.290 2 | 4 982 041.618 3 | 2 781 470.180 5 |
式中,m是控制点的个数,分别采用最小二乘、加权总体最小二乘法以及本文方法(STLS)(以最小二乘解为初值)来进行求解,解算的结果如表 2所示,测向量和系数矩阵的改正值的结果如表 3所示。
| 估计方法 | ΔX/m | ΔY/m | ΔZ/m | ωX/(10-5rad) | ωY/(10-5rad) | ωZ/(10-5rad) | m | σ0/mm |
| LS | -3.879 4 | 7.231 9 | 3.952 0 | 0.304 2 | -0.690 2 | 1.696 7 | 0.999 999 04 | 3.975 |
| WTLS | -3.879 4 | 7.231 9 | 3.951 9 | 0.304 2 | -0.690 2 | 1.696 7 | 0.999 999 04 | 2.810 |
| STLS | -3.879 4 | 7.231 9 | 3.951 9 | 0.304 2 | -0.690 2 | 1.696 7 | 0.999 999 04 | 2.810 |
| EA | VL | ||||||
| 0 | 0 | 0 | 0 | -0.000 560 489 3 | -0.001 881 515 3 | -0.002 667 601 6 | 0.002 667 632 2 |
| 0 | 0 | 0 | 0.000 560 489 3 | 0 | 0.002 667 601 6 | -0.001 881 515 3 | 0.001 881 470 1 |
| 0 | 0 | 0 | 0.001 881 515 3 | -0.002 667 601 6 | 0 | 0.000 560 489 3 | -0.000 560 514 0 |
| 0 | 0 | 0 | 0 | -0.001 121 354 1 | -0.000 727 307 2 | -0.000 280 937 3 | 0.000 280 942 1 |
| 0 | 0 | 0 | 0.001 121 354 1 | 0 | 0.000 280 937 3 | -0.000 727 307 2 | 0.000 727 299 7 |
| 0 | 0 | 0 | 0.000 727 307 2 | -0.000 280 937 3 | 0 | 0.001 121 354 1 | -0.001 121 359 3 |
| 0 | 0 | 0 | 0 | 0.000 040 802 3 | 0.000 963 434 9 | 0.001 581 488 4 | -0.001 581 506 0 |
| 0 | 0 | 0 | -0.000 040 802 3 | 0 | -0.001 581 488 4 | 0.000 963 434 9 | -0.000 963 408 8 |
| 0 | 0 | 0 | -0.000 963 434 9 | 0.001 581 488 4 | 0 | -0.000 040 802 3 | 0.000 040 816 2 |
| 0 | 0 | 0 | 0 | 0.000 087 627 9 | 0.000 672 184 1 | 0.001 203 295 1 | -0.001 203 307 0 |
| 0 | 0 | 0 | -0.000 087 627 9 | 0 | -0.001 203 295 1 | 0.000 672 184 1 | -0.000 672 164 0 |
| 0 | 0 | 0 | -0.000 672 184 1 | 0.001 203 295 1 | 0 | -0.000 087 627 9 | 0.000 087 638 3 |
| 0 | 0 | 0 | 0 | 0.000 867 451 5 | -0.0010519521 | -0.002 577 559 9 | 0.002 577 586 2 |
| 0 | 0 | 0 | -0.000 867 451 5 | 0 | 0.002 577 559 9 | -0.001 051 952 1 | 0.001 051 912 0 |
| 0 | 0 | 0 | 0.001 051 952 1 | -0.002 577 559 9 | 0 | -0.000 867 451 5 | 0.000 867 431 3 |
| 0 | 0 | 0 | 0 | -0.002 711 875 1 | 0.001 149 986 6 | 0.004 651 481 7 | -0.004 651 524 4 |
| 0 | 0 | 0 | 0.002 711 875 1 | 0 | -0.004 651 481 7 | 0.001 149 986 6 | -0.001 149 917 0 |
| 0 | 0 | 0 | -0.001 149 986 6 | 0.004 651 481 7 | 0 | 0.002 711 875 1 | -0.002 711 842 1 |
| 0 | 0 | 0 | 0 | 0.000 787 089 9 | -0.001 657 898 9 | -0.003 775 224 1 | 0.003 775 261 3 |
| 0 | 0 | 0 | -0.000 787 089 9 | 0 | 0.003 775 224 1 | -0.001 657 898 9 | 0.001 657 838 8 |
| 0 | 0 | 0 | 0.001 657 898 9 | -0.003 775 224 1 | 0 | -0.000 787 089 9 | 0.000 787 059 5 |
| 0 | 0 | 0 | 0 | 0.000 317 22 6 | -0.001 373 758 7 | -0.002 689 293 7 | 0.002 689 321 8 |
| 0 | 0 | 0 | -0.000 317 229 6 | 0 | 0.002 689 293 7 | -0.001 373 758 7 | 0.001 373 715 3 |
| 0 | 0 | 0 | 0.001 373 758 7 | -0.002 689 293 7 | 0 | -0.000 317 229 6 | 0.000 317 207 1 |
| 0 | 0 | 0 | 0 | 0.000 144 018 7 | 0.000 280 227 1 | 0.000 283 067 5 | -0.000 283 071 5 |
| 0 | 0 | 0 | -0.000 144 018 7 | 0 | -0.000 283 067 5 | 0.000 280 227 1 | -0.000 280 222 1 |
| 0 | 0 | 0 | -0.000 280 227 1 | 0.000 283 067 5 | 0 | -0.000 144 018 7 | 0.000 144 021 6 |
| 0 | 0 | 0 | 0 | 0.000 651 659 4 | 0.001 445 333 9 | 0.002 010 251 0 | -0.002 010 272 9 |
| 0 | 0 | 0 | -0.000 651 659 4 | 0 | -0.002 010 251 0 | 0.001 445 333 9 | -0.001 445 299 2 |
| 0 | 0 | 0 | -0.001 445 333 9 | 0.002 010 251 0 | 0 | -0.000 651 659 4 | 0.000 651 678 3 |
| 0 | 0 | 0 | 0 | 0.001 497 839 3 | 0.002 181 265 7 | 0.002 261 033 0 | -0.002 261 061 9 |
| 0 | 0 | 0 | -0.001 497 839 3 | 0 | -0.002 261 033 0 | 0.002 181 265 7 | -0.002 181 224 8 |
| 0 | 0 | 0 | -0.002 181 265 7 | 0.002 261 033 0 | 0 | -0.001 497 839 3 | 0.001 497 863 0 |
从表 2可以发现,采用本文方法按照混合结构总体最小二乘算法得到的平差结果与加权总体最小二乘的结果完全一致,且单位权中误差都较最小二乘法小。从表 3可以看出,采用本文方法求得的系数矩阵的改正值完全符合系数矩阵的结构规律,即保证系数矩阵相同元素得到相同的改正数,常数项的改正数为0,这与采用加权总体最小二乘法得到的结果一致,但相比之下,本文方法更方便。因为本文方法通过构造结构矩阵来估计系数矩阵的重复元素和常数项。对于三维坐标转换的布尔沙转换模型,结构矩阵中的4个矩阵R是固定的,只需根据参与平差时的控制点个数来最终确定矩阵D。而采用加权总体最小二乘法在构造权矩阵时是比较麻烦的(详见文献[6]),相比之下,通过本文方法构造的结构矩阵的规律性更强,平差解算较为简单。
3 结 语1) 本文根据非线性最小二乘平差理论,并采用构造结构矩阵的方法来顾及系数矩阵的常数项和重复元素,提出了一种EIV模型参数估计新方法,并详细推导了其解算步骤。该方法将测量数据处理中的总体最小二乘(包括混合总体最小二乘)、加权总体最小二乘以及结构总体最小二乘(包括混合总体最小二乘)等3种算法统一起来。算法的推导过程及迭代格式简单,且易于理解。
2)新方法不仅推导了参数的求解算法,而且给出了参数的精度评定公式,通过算例的分析并与文献中的算法进行比较,验证了公式的正确性。
3)将本文的新方法通过两个算例进行分析,结果验证了本文的方法能运用到总体最小二乘、加权总体最小二乘以及结构总体最小二乘等3种算法中。
| [1] | Golub G H, van Loan. An Analysis of the Total Least Squares Problem[J].SIAM J Numer Anal, 1980, 17: 883-893 |
| [2] | Kong Jian,Yao Yibin,Wu Han.Iterative Method for Total Least-Squares[J]. Geomatics and Information Science of Wuhan University, 2010,35(6):711-714(孔建,姚宜斌,吴寒. 整体最小二乘的迭代解法[J].武汉大学学报·信息科学版,2010,35(6): 711-714) |
| [3] | Wang Qisheng,Yang Dehong,Yang Jianwen. An Iteration Algorithm of Linear Regression Based on Total Least Squares[J].Journal of geodesy and geodynamics,2013,33(6):112-114(汪奇生,杨德宏,杨建文. 基于总体最小二乘的线性回归迭代算法[J]. 大地测量与地球动力学,2013,33(6):112-114) |
| [4] | Qiu Weining,Tao Benzhao,Yao Yibin, et al. The Theory and Method of Surveying Data Processing [M]. Wuhan: Wuhan University Press, 2008(邱卫宁,陶本藻,姚宜斌,等.测量数据处理理论与方法[M].武汉: 武汉大学出版社,2008) |
| [5] | Ding Keliang, Sheng Yunzhong, Ou Jikun.Methods of Line Fitting Based on Total Least-Squares[J]. Journal of Liaoning Technical University (Natural Science),2010,29(1): 44-47(丁克良,沈云中,欧吉坤. 整体最小二乘法直线拟合[J]. 辽宁工程技术大学学报(自然科学版), 2010,29(1) :44-47) |
| [6] | Yuan Qing, Lou Lizhi, Chen Weixian.The Application of the Weighted Total Least-Squares on Three Dimensional-Datum Transformation[J]. Acta Geodaetica et Cartographica Sinica, 2011,(Supp.): 115-119)(袁庆, 楼立志, 陈玮娴. 加权总体最小二乘在三维基准转换中的应用[J]. 测绘学报, 2011(增刊): 115-119) |
| [7] | Schaffrin B,Wieser A. On Weighted Total Least-Squares Adjustment for Linear Regression [J]. Journal of Geodesy, 2008,82(7): 415-421 |
| [8] | Shen Y Z,Li B F, Chen Y. An Iterative Solution of Weighted Total Least-Squares Adjustment[J]. Journal of Geodesy,2011, 85(4): 229-238 |
| [9] | Xu P L,Liu J N,Shi C.Total Least Squares Adjustment in Partial Errors-in-variables Models: Algorithm and Statistical Analysis[J]. Journal of Geodesy,2012, 86:661-675 |
| [10] | Mahboub V.On Weighted Total Least-Squares for Geodetic Transformations [J].Journal of Geodesy, 2012,86(5): 359-367 |
| [11] | Hu Chuan,Chen Yi, Peng You. On Mixed Structured Total Least Squares for Paramet Ersestimation[J].Journal of Geodesy and Geodynamics,2013,33(4):56-60(胡川,陈义,彭友.混合结构总体最小二乘参数估计[J].大地测量与地球动力学, 2013, 33(4): 56-60) |
| [12] | Liu Jingnan,Zeng Wenxian,Xu Peiliang. Overview of Total Least Squares Methods[J]. Geomatics and Information Science of Wuhan University, 2013, 38(5): 505-512(刘经南,曾文宪,徐培亮.整体最小二乘估计的研究进展[J].武汉大学学报·信息科学版, 2013, 38(5): 505-512) |
 2016, Vol. 41
2016, Vol. 41


