文章信息
- 孙文川, 暴景阳, 金绍华, 肖付民, 崔杨
- SUN Wenchuan, BAO Jingyang, JIN Shaohua, XIAO Fumin, CUI Yang
- 多波束海底地形畸变校正与声速剖面反演
- Inversion of Sound Velocity Profiles by Correcting the Terrain Distortion
- 武汉大学学报·信息科学版, 2016, 41(3): 349-355
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 349-355
- http://dx.doi.org/10.13203/j.whugis20140142
-
文章历史
- 收稿日期: 2014-10-22

2. 大连舰艇学院海洋测绘系, 辽宁 大连, 116018
2. Department of Hydrography and Cartography, Dalian Naval Academy, Dalian 116018, China
声速剖面采样是多波束测深过程中测区声速信息的主要获取方式。目前,我国声速剖面站的布设时间均是一天内水温变化的极值点附近(每天的早晨8点、中午2点和晚上8点),声速剖面改正主要采用时间就近原则[1],由于声速剖面在时间上和空间上的可变性[2],采用以上方法进行声速改正必然导致有限的声速剖面数据不能满足水深数据进行声速改正的精度要求,从而引入测深误差,导致海底地形的畸变;在使用CARIS HIPS软件系统进行水深数据处理过程中,通过调整Refraction选项卡的Coefficients参数,以人工干预的方式削弱声速误差对水深数据的影响,该方法虽然有效,但人工的干预既缺乏数学依据,又降低了多波束数据的处理效率。
国内外的研究表明,在近海和远洋海域,声速变化呈现一定的规律性,在一定程度上是可以预估的[1, 2, 3]。声速剖面结构参数化模型能够实现对声速剖面数据的简化描述与扩展[4, 5],其中经验正交函数能够利用海洋中声速剖面数据的时空相关性,通过对具有相同特性的声速剖面群(同一水域内多个声速剖面)进行特征向量提取(模态分解),进而结合采样数据重构连续的声速剖面。LeBlanc等的研究表明,EOF是描述声速剖面最有效的基函数[6, 7],近年来的相关研究证明了这种方法的可行性和有效性[8, 9, 10]。
本文基于以上特点(本文基于多波束作业实测数据),对测区内采集的实测声速剖面数据进行EOF特征向量提取;结合遗传算法,重构与水深对应的声速剖面对畸变海底回波数据进行声速改正;以畸变改正量为依据对声速剖面重构结果进行优化,最终反演出测区内对应水深数据的声速剖面,实现对测区内声速剖面的加密。实例计算表明,采用本文方法得到的声速剖面与实际声速剖面有较好的一致性,用改正后的水深数据能较好地解决因声速误差引起的海底地形畸变;在克服了传统声速剖面改正方法不足的同时,有效地提高了水深数据的测量精度和数据处理效率。
1 声速误差引起海底地形畸变由于海水介质各层的温度、盐度和压力的不同,导致了海水中各层声速的变化,进而引起声线传播方向不断地偏折和弯曲。如果使用平均声速或不正确的声速剖面,声速剖面的差异将通过声线弯曲直接影响海底探测精度,导致海底形态的畸变[2, 11, 12, 13, 14]。因此,在采用替代声速剖面(时间或距离最近的声速剖面,而非实时获得的声速剖面)进行水深数据声速改正时,声速剖面的差异必然会影响水深数据的声速改正结果,引入附加的水深误差,易产生海底地形畸变。
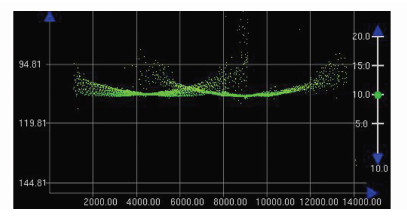
当表层声速偏小,下部声速偏大,测量时会在水深条带横向剖面上出现对称上翘,即虚假的凹形地形;若表层声速偏大,下部偏小则表现为对称下弯,即凸形地形。如果相邻两个测深条带都出现地形畸变,在两个测深条带的重叠处就会出现沿着航迹方向的“沟垄”或“脊背”[11, 15]。如图 1所示,由于声速误差的影响,两个测深条带都出现了因声速误差引起的典型的凹形地形(“笑脸”),在条带重叠处出现了明显的“脊背”。
|
| 图 1 声速误差引起的地形畸变 Fig. 1 Terrain Distortion Caused by the Sound Velocity Errors |
海洋声学反演是通过观测数据推测海洋声传播介质特征及其参数的研究手段之一,国内外许多学者也提出了一些利用水声设备反演海水声速剖面的方法[16, 17, 18, 19, 20, 21]。本文通过对测区内实测的声速剖面采样数据进行EOF分析,即可得到能够代表测区声速变化规律的模态向量和声速剖面重构系数范围;以此为依据重构声速剖面,对平坦海底的水深数据进行声速改正,结合改正后畸变海底的地形改正程度构建适应度函数,通过遗传算法[22],确定此处水深数据对应声速剖面的最佳重构系数,从而达到对水深数据所对应的声速剖面进行反演的目的。
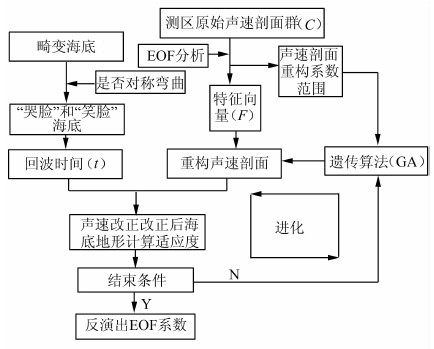
2.1 基于平坦海底地形形变的声速剖面反演流程对多波束扫测过的水域进行声速剖面反演,其过程如图 2所示。
|
| 图 2 遗传算法反演声速剖面流程 Fig. 2 Flowchart of Inversion of Sound Velocity Profile by GA |
1) 在水深数据中选取畸变海底对应的水深数据(呈现左右对称的“哭脸”或“笑脸”回波序列),记录其回波时间(从原始数据包中提取回波时间),同时将测区内实测的声速剖面群进行EOF分解得到测区声速剖面的特征向量,并计算重构系数的取值范围;
2) 依据得到的重构系数范围初始化种群,得到初始的声速剖面重构系数,其与特征向量结合得到重构的声速剖面;
3) 将得到的声速剖面用于对回波序列进行声速改正,得到改正后的海底地形并计算其适应度,经过遗传算法的进化过程,声速剖面的重构系数被逐渐优化,适应度较高的个体(即接近真实声速剖面的重构系数)被保存下来,保存下来的个体继续重复以上的进化过程;
4) 最后,当进化过程满足结束条件时,最为优秀的个体(最优的重构系数)被保存下来,再经过EOF重构过程,得到与水深数据相对应的声速剖面反演结果。
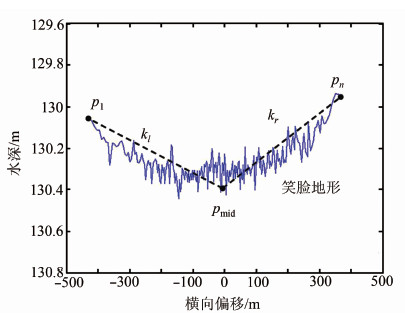
2.2 基于海底地形畸变程度的适应度构建由上述分析可知,平坦海底得到的回波时间由于采用了错误的声速剖面进行声速改正,出现了“哭脸”和“笑脸”地形;如图 3所示,当“笑脸”地形出现时,多波束测量的1 ping水深由左至右呈现先增大后减小的趋势,其与真实海底(水深值均匀变化)存在显著差异,为了判断地形畸变的大小,构造适应度函数如下:
|
| 图 3 适应度函数构造示意图 Fig. 3 Construction of the Fitness Function |
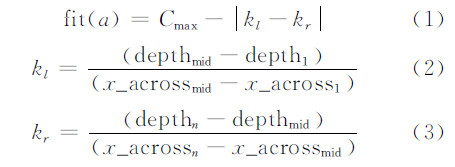
式中depthi为第i个波束所对应的水深值;x_acrossmid为中央波束所对应的横向偏移。如图 3中所示,以中央波束为界,将1 ping的水深点分为左右两部分,分别求左半部分的斜率kl和右半部分的斜率kr。当“笑脸”地形出现时,1 ping水深出现起伏,丨kl-kr丨≠0,且“笑脸”地形越明显时,丨kl-kr丨的值也越大;当丨kl-kr丨=0时,地形接近平坦海底,为了使平坦的海底有较大的适应度,式中加入了较大的常数Cmax,当海底趋于平坦时,fit(a)变大且趋于Cmax(即所采用的声速剖面趋近于真实声速剖面),使较优秀的个体能够在进化过程中被保存下来。
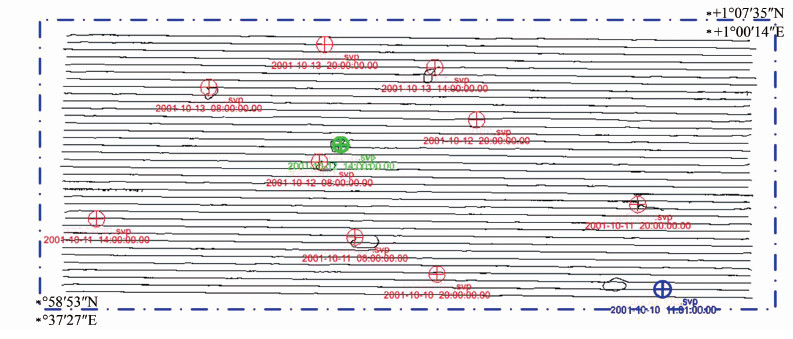
3 实例计算 3.1 消除海底地形形变反演声速剖面 3.1.1 反演声速剖面位于测区中央为了验证反演方法的有效性,实验选取°一次测量任务中测区(测区范围为:*°58′53″N,*37′27″E~*+1°07′35″N,*+1°00′14″E)内连续3 d(10月10日~10月13日)测得的11组声速剖面数据(图 4中十字标记)和48条测线(图 4中黑线)。
|
| 图 4 测区声速剖面分布图 Fig. 4 Disribution of Sound Velocity Profile in Survey Area |
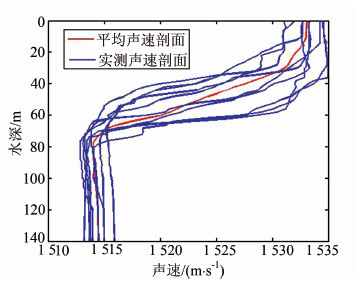
首先从11个声速剖面中选取一个实测声速剖面(图 4中测区中部粗十字标记)作为待反演声速剖面(选取的实测声速剖面仅用于和反演结果进行比对,不参与反演运算),用剩余的10组声速剖面(图 4中十字标记)按时间最近法则对测区内水深数据进行声速改正;选取因声速剖面缺失(待反演声速剖面附近)造成水深出现“笑脸”的70 ping数据(图 1)作为形变海底;对选取的10组声速剖面进行EOF分析(图 5、图 6),得到模态向量和重构系数取值范围(表 1)。
| 反演参数 | 参数标识 | 下边界 | 上边界 |
| 第一阶 | a1 | -85.23 | 87.88 |
| 第二阶 | a2 | -27.13 | 28.08 |
| 第三阶 | a3 | -14.21 | 13.79 |
| 第四阶 | a4 | -11.40 | 11.20 |
| 第五阶 | a5 | -9.08 | 11.53 |
| 第六阶 | a6 | -8.66 | 7.82 |
|
| 图 5 实测声速剖面 Fig. 5 Real Sound Velocity Profiles |
|
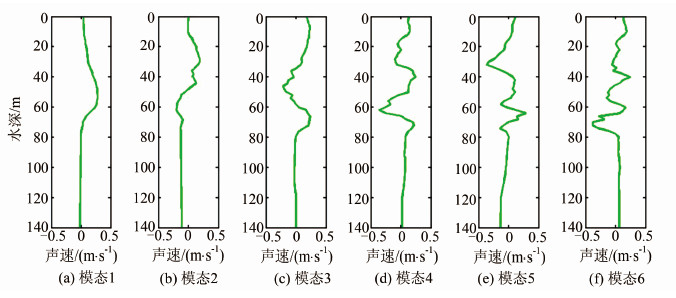
| 图 6 实测声速剖面提取模态向量 Fig. 6 Mode Vectors of Real Sound Velocity Profiles |
取其前6维向量(图 6)(研究证明,前6维向量所能表示声速剖面起伏的能量百分比能达到96%以上[14, 23])和水深数据中随机抽取的第22ping回波数据按§2.1中的方法进行声速剖面反演。根据表 1中的EOF重构系数范围初始化种群,其中,种群大小为50,杂交概率为0.8,变异概率为0.15;采用2.2中构建的适应度函数,取Cmax=100,进行2 000代进化,得到优化的声速剖面重构系数(a1=16.90,a2=9.14,a3=11.35,a4=-6.02,a5=-5.35,a6=-5.31),用其重构的声速剖面(图 7中星线)对第22 ping水深数据进行声速改正,得到海底地形(图 8中星线)。
|
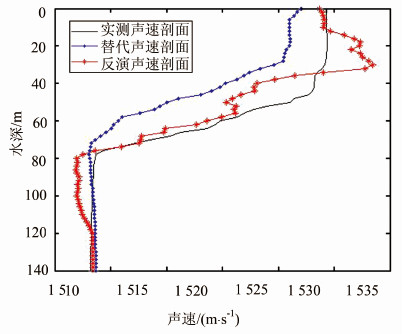
| 图 7 测区中央声速剖面对比 Fig. 7 Comparison of Sound Velocity Profiles in the Middle of Survey Area |
|
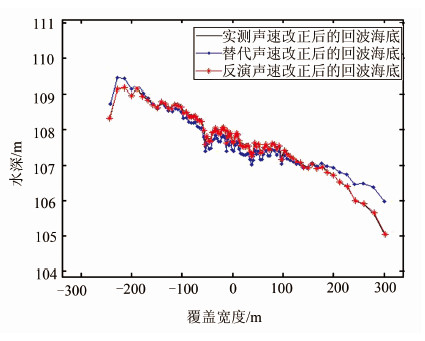
| 图 8 不同声速改正后水深效果图 Fig. 8 Terrains Corrected by Sound Velocity Profiles |
图 7中,实线为实验前选取的实测待反演声速剖面,点线为依据时间最近原则选取的声速剖面(替代声速剖面),星线为本文方法反演得到的声速剖面。由图中可以看到,反演得到声速剖面的变化趋势和实测声速剖面更为接近(通常,通过声学信号反演海水声速剖面只能得到声传播路径上等效声速剖面[15],由于用来进行反演的10个声速剖面的跃层分别出现在10~60 m之间,导致反演结果在10~60 m之间出现围绕实测声速剖面的波动,形成了小范围的等效声速剖面);将替代声速剖面和反演声速剖面分别与实测声速剖面进行比对,其误差统计结果如表 2所示,反演得到的声速剖面结果更加接近实测声速剖面,其误差的均值和中误差都优于替代声速剖面。
| /(m·s-1) | ||||
| 误差 | 最大值 | 最小值 | 平均值 | 中误差 |
| 替代SVP | 11.10 | 0.02 | -3.12 | 3.64 |
| 反演SVP | 6.07 | 0.03 | -0.69 | 2.19 |
将用于反演的第22 ping回波时间经不同声速剖面改正后的水深效果如图 8所示,从图中可以看出,由反演得到的声速剖面进行声速改正后的海底地形更为接近真实海底;其与真实水深的误差较之替代声速剖面更小(表 3),达到厘米级,具有更高的精度。
| /m | ||||
| 误差 | 最大值 | 最小值 | 平均值 | 中误差 |
| 替代SVP | 0.97 | 0.01 | -0.12 | 0.25 |
| 反演SVP | 0.06 | 0.00 | -0.04 | 0.03 |
为了进一步验证反演方法的有效性,在此对位于测区边缘(图 4中测区右下角粗十字标记的声速剖面,采集时间为2001年10月10日 13:31:00)的声速剖面进行反演,采用剩余的10组声速剖面和测线编号为001的水深数据进行声速反演,其反演结果如图 9所示。
|
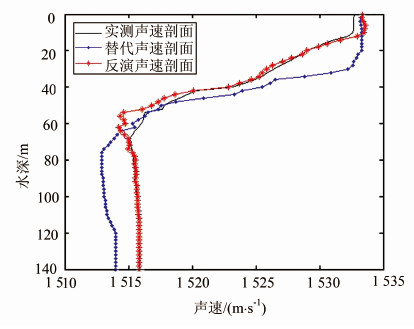
| 图 9 测区边缘声速剖面对比 Fig. 9 Comparison of Sound Velocity Profiles in the Edge of Survey Area |
图 9中黑色实线为实验前选取的实测待反演声速剖面(采集时间为2001年10月10日 13:31:00),虚线为依据时间最近原则选取的声速剖面(替代声速剖面,采集时间为2001年10月10日 20:00:00),星线为本文方法反演得到的声速剖面。显然,反演的声速剖面较替代声速剖面更为接近实测声速剖面,对应的声速剖面误差统计结果(表 4)和水深误差统计结果(表 5)均显示反演得到的声速剖面与实测声速剖面间的误差较小,其对应的水深数据声速改正结果也更加接近真实海底,具有较高的精度,说明本文方法对测区边缘的声速剖面也有较好的反演效果。
| /(m·s-1) | ||||
| 误差 | 最大值 | 最小值 | 平均值 | 中误差 |
| 替代SVP | 5.80 | -2.60 | -0.25 | 2.52 |
| 反演SVP | 0.87 | -1.89 | -0.18 | 0.60 |
| /m | ||||
| 误差 | 最大值 | 最小值 | 平均值 | 中误差 |
| 替代SVP | 0.48 | -0.02 | 0.06 | 0.10 |
| 反演SVP | 0.02 | 0.08 | 0.04 | 0.02 |
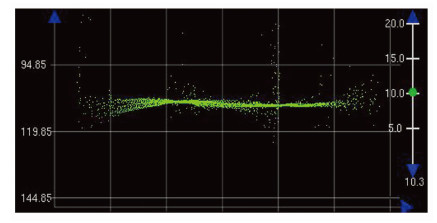
分别对图 1中相邻两个条带对应的声速剖面进行反演,用得到的反演声速剖面对两条带测深数据(连续)进行声速改正,改正效果如图 10,用反演的声速剖面进行声速改正后的水深数据,与图 1对比,其有效地削弱了因声速误差引起的地形弯曲;在条带重叠处,因声速误差引起的“脊背”现象也得到了明显的改善,条带间水深平滑过渡,条带拼接良好,再次证明了反演声速剖面的有效性。
|
| 图 10 经反演声速剖面改正后的水深数据 Fig. 10 Terrains Corrected by the Inversion Result of Sound Velocity Profile |
在分析了声速剖面误差对海底地形影响的基础上,将声速剖面EOF分析方法和遗传算法相结合,依据海底地形畸变程度构造适应度函数,提出了通过校正地形畸变反演声速剖面的方法。实例计算表明,本文的声速剖面反演方法能较好的消除因声速误差引起的多波束条带测深数据的“哭笑脸”现象;通过声速剖面的比对证明了反演声速剖面较替代声速剖面更接近声速剖面的实测值;最后对加密前后水深误差进行统计,论证了经本文方法得到的声速剖面改正后的水深数据具有更高的精度,缩小了条带重叠处的水深差异。
| [1] | Zhu Xiaochen. Research on Data Processing Critical Modeling and Application on Multibeamecho Sounding[D]. Dalian: Dalian Naval Academy, 2011(朱小辰. 多波束测深数据处理关键模型及应用研究[D]. 大连:海军大连舰艇学院,2011) |
| [2] | Li Jiabiao. Principles Multibeam Survey Techniques and Methods[M]. Beijing: Ocean Press, 1999 (李家彪.多波束勘测原理技术与方法[M]. 北京:海洋出版社,1999) |
| [3] | Kammerer E, John E, Clarke H. New Method for the Removal of Refraction Artifacts in Multibeam Echosounder Systems[C]. Canadian Hydrographic Conference Montréal, Canada, 2000 |
| [4] | Zhang Xu, Zhang Yonggang, Zhang Jianxue, et al. A New Model for Calculating Sound Speed Profile Structure[J]. Acta Oceanologica Sinica, 2011, 33(5): 54-60(张旭, 张永刚, 张健雪, 等. 一种新的声速剖面结构参数化方法[J]. 海洋学报, 2011, 33(5): 54-60) |
| [5] | Ding Jisheng, Zhou Xinghua, Tang Qiuhua, et al. Expression of Multi-beam Echo Sounding Sound Velocity Profile with Empirical Orthogonal Functions [J]. Geomatics and Information Science of Wuhan University,2007, 32(5): 446-449(丁继胜, 周兴华, 唐秋华, 等. 多波束勘测声速剖面场的EOF表示方法[J]. 武汉大学学报·信息科学版, 2007, 32(5): 446-449) |
| [6] | Blanc L R, Middleton F H. An Underwater Acoustic Sound Velocity Data Model [J]. J Acoust Soc Am, 1980, 67: 2 055-2 062 |
| [7] | Shen Yuanhai, Ma Yuanliang, Tu Qingping, et al. Feasibility of Description of the Sound Speed Profile in Shallow Water via Empirical Orthogonal Function (EOF) [J]. Applied Acoustics, 1999, 18(2): 21-25(沈远海, 马远良, 屠庆平, 等. 浅水声速剖面用经验正交函数(EOF) 表示的可行性研究[J]. 应用声学, 1999, 18(2): 21-25) |
| [8] | Peng Linhui, Wang Ning, Qiu Xiaofeng, et al. Modal Wave Number Tomography for South China Sea Front[J]. China Ocean Engineering, 2003, 17(2): 289-294 |
| [9] | He Li, Li Zhenglin, Zhang Renhe, et al. Expression of Sounding Sound Velocity Profile with EOF and Matched Field Inversion in East China Sea[J]. Progress in Natural Science, 2006, 16(3): 351-355(何利, 李整林, 张仁和, 等. 东中国海声速剖面的经验正交函数表示与匹配场反演[J]. 自然科学进展, 2006, 16(3): 351-355) |
| [10] | Dong Qingliang, Han Hongqi, Fang Zhaobao,et al. The Influence of Sound Speed Profiles Correction on Multibeam Survey[J]. Hydrographic Surveying and Charting, 2007,27(2): 56-58(董庆亮, 韩红旗, 方兆宝, 等. 声速剖面改正对多波束测深的影响[J]. 海洋测绘, 2007,27(2): 56-58) |
| [11] | Li Jiabiao, Zheng Yulong, Wang Xiaobo, et al. The Main Affecting Factors of Multibeam Bathymetry Accuracy[J]. Hydrographic Surveying and Charting, 2001,21(1): 26-32(李家彪, 郑玉龙, 王小波, 等. 多波束测深及影响精度的主要因素[J]. 海洋测绘, 2001,21(1): 26-32) |
| [12] | Zhao Jianhu, Liu Jingnan. Multibeam Bathymetric Survey and Image Processing[M]. Wuhan: Wuhan University Press, 2009(赵建虎, 刘经南. 多波束测深及图像数据处理[M]. 武汉: 武汉大学出版社, 2008) |
| [13] | Dong Qingliang, Cui Minxun, Zhou Junhua, et al. Analysis and Processing of Transform Geography of Convex and Cave in Multibeam Sounding System[J]. Hydrographic Surveying and Charting, 2011, 31(1): 32-35(董庆亮, 崔民勋, 周君华, 等. 多波束测深系统中凹凸变形地形的分析与处理[J]. 海洋测绘, 2011, 31(1): 32-35) |
| [14] | He Li, Li Zhenglin, Peng Zhaohui, et al. Inversion for Sound Speed Profiles in the Northern of South China Sea[J]. Scientia Sinica Phys, Mech & Astron, 2011, 41(1): 49-57(何利, 李整林, 彭朝晖, 等. 南海北部海水声速剖面声学反演[J]. 中国科学(物理学,力学,天文学), 2011, 41(1): 49-57) |
| [15] | Jin G, Lynch J F, Chiu C S, et al. A Theoretical and Simulation Study of Acoustic Normal Mode Coupling Effects Due to the Barents Sea Polar Front with Applications to Acoustic Tomography and Matched Field Processing[J]. J Acoust Soc Am, 1996, 101(1): 193-205 |
| [16] | Lindsay C E, Chapman N R. Matched Field in Version Study of Geo Acoustic Model Parameter Using Adaptive Simulated Annealing[J]. IEEE Journal of Oceanic Engineering, 1993, 18(3): 224-231 |
| [17] | Vaccaro R J. The Past, Present and Future of Underwater Acoustic Signal Processing[J] . IEEE Signal Processing Magazine, 1998, 7: 21-51 |
| [18] | Zhang Zhongbing, Ma Yuanliang, Ni Jinping, et al. A New and Practical Method for Inverting Sound Speed Profile in Shallow Water[J]. Journal of Northwestern Polytechnical University, 2002, 20(1) : 36-39(张忠兵, 马远良, 倪晋平, 等. 基于声线到达时差的浅海声速剖面反演[J]. 西北工业大学学报, 2002, 20(1) : 36-39) |
| [19] | Lei Yingjie, Zhang Shanwen, Li Xuwu, et al. MATLAB Genetic Algorithm Toolbox and Application[M]. Xi'an: Xi'an University of Electronic Science and Techonoldgy Press, 2005(雷英杰, 张善文,李续武, 等. MATLAB遗传算法工具箱及应用[M]. 西安: 西安电子科技大学出版社, 2005) |
| [20] | Zhang Xu, Zhang Yonggang, Zhang Jianxue, et al. EOF Analysis of Sound Speed Profile in East Water of Taiwan[J]. Advances in Marine Science,2010, 28(4): 498-506(张旭, 张永刚, 张健雪, 等. 台湾以东海域声速剖面序列的EOF分析[J]. 海洋科学进展, 2010, 28(4): 498-506) |
| [21] | Lu Xiuping, Bian Shaofeng, Huang Motao, et al. An Improved Method for Calculating Average Sound Speed in Constant Gradient Sound Ray Tracing Technology[J]. Geomatics and Information Science of Wuhan University,2012, 37(5): 590-593 (陆秀平, 边少锋, 黄谟涛, 等. 常梯度声线跟踪中平均声速的改进算法[J]. 武汉大学学报·信息科学版, 2012, 37(5): 590-593) |
| [22] | Zhao Jianhu, Zhou Fengnian, Zhang Hongmei, et al. Classification of Sound Speed Profile with SOFM Neuron Network [J]. Geomatics and Information Science of Wuhan University,2007, 32(2): 164-167(赵建虎, 周丰年, 张红梅, 等. 基于自组织神经网络的声速剖面分类方法研究[J]. 武汉大学学报·信息科学版, 2007, 32(2): 164-167) |
| [23] | Zhao Jianhu, Zhou Fengnian, Zhang Hongmei, et al. Establishment of Spatial Model for Sound Velocity in Local [J]. Geomatics and Information Science of Wuhan University,2008, 32(2): 199-202(赵建虎, 周丰年, 张红梅, 等.局域空间声速模型的建立方法研究[J]. 武汉大学学报·信息科学版, 2008, 33(2): 199-202) |
 2016, Vol. 41
2016, Vol. 41


