文章信息
- 郭东美, 鲍李峰, 许厚泽
- GUO Dongmei, BAO Lifeng, XU Houze
- 中国大陆厘米级大地水准面的地形影响分析
- Analysis of Terrain Effects in cm-order Geoid Computations in Chinese Mainland
- 武汉大学学报·信息科学版, 2016, 41(3): 342-348
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 342-348
- http://dx.doi.org/10.13203/j.whugis20130494
-
文章历史
- 收稿日期: 2014-03-05

2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 湖北 武汉, 430077
2. State Key Laboratoty of Geodesy and Earth's Dynamics, Wuhan 430077, China
随着航空重力和卫星重力的快速发展,精确处理地球外空间各种类型重力场元的地形影响已成为地球重力场面临的重要课题。同时厘米级大地水准面精化对地形影响处理技术提出了更高要求,研究开发适合厘米级精度的地形影响算法,已成为厘米级大地水准面能否实现的关键因素之一。目前大地水准面计算中地形影响通常采用地形改正[1, 2]或Molodensky算法[3]进行处理,本文研究在传统方法的基础上提出改进,以满足当前高精度重力场计算的需要。
对于地形改正,按采用的基准面的不同可以分为平面地形改正[4]、球面地形改正和椭球面地形改正[5]。平面地形改正法将适合观测数据范围较小且地形起伏不大的数据预处理。然而对于区域性的,乃至全球尺度问题,需要利用球坐标进行表达与处理。此时建立在直角坐标系中的数据处理、分析及反演解释方法已不再适用[6]。现在地面重力勘探工作多处于地形起伏较大地区,且航空重力和卫星重力则需要对大范围的数据进行处理,发展球坐标系内高精度的地形改正方法显得尤其重要。鉴于此,本文提出基于国际通用的GRS80椭球采用空间域Tesseroid单元体[7]引力效应计算地形改正的方法,以适合于观测数据范围较大或地形起伏较大的地形数据预处理。
对于Molodensky边值问题[8, 9],由于以地球近似表面作为边界面,不需作与地球质量及地球密度相关的各种改正(如布格改正、均衡改正、赫尔默特压缩等),因而该边值问题始终是物理大地测量中的重要研究方向。目前,在对似大地水准面计算中,通常只考虑Molodensky一阶项对高程异常的贡献。但是已有结果表明,对于一般山区地形影响二阶项能达到1 dm,对于高山区能达到几dm,而且当地形倾角很大时高阶项存在不收敛现象[10]。因此,对于我国厘米级似大地水准面精化任务,需要顾及二阶项甚至更高阶项对高程异常的贡献。如何准确计算Molodensky高阶项对高程异常的影响是大地水准面实现优于厘米级精度必须解决的关键问题之一。本文基于Molodensky级数解算法,以Molodensky一阶项公式为依据,建立高阶项对高程异常影响的模型,研究实现Molodensky Ⅰ/Ⅱ及高阶项对高程异常贡献的高精度算法。
此外,我国目前计算重力大地水准面时,通常方案是采用地形改正代替Molodensky一阶项进行计算。但是从理论上讲,重力大地水准面的计算应采用严格的Molodensky公式,采用局部地形改正代替Molodensky一阶项计算重力大地水准面虽然可节省大量计算时间,但却又是一种近似的方法,其近似性的影响有多大迄今未见研究。本文利用地形改正代替Molodensky级数解计算了重力大地水准面的近似误差。
1 厘米级精度的高程异常地形影响的计算方法与模型 1.1 质量棱柱积分与质量线积分地形校正方法相对于点P(xP,yP,hP),地形改正的公式为[10]:
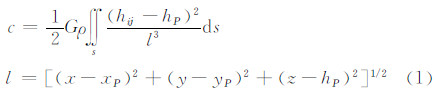
式中,hij和hP 分别是流动点Q和积分点P的高程;G为牛顿引力常数;ρ为地形密度(假设为常数)。
在实际计算时,DTM 通常以规则格网数据表示,并假定每个格网内的地形用一个质量均匀分布而高程不变的棱柱体代替,则得到用质量棱柱地形模型表示的地形改正公式为:
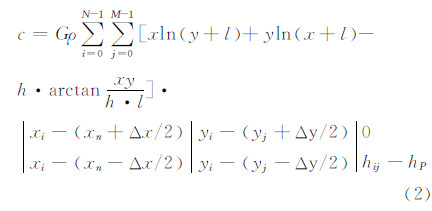
在上述质量棱柱地形模型中,如果假设地形质量集中分布于柱体中心线上,则用质量线地形模型表示的地形改正公式为:
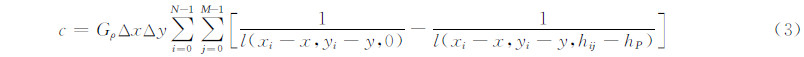
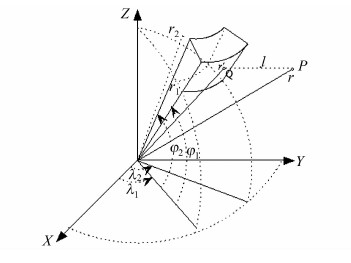
扇形柱体概念最早由 Anderson于1976年提出[11]。扇形柱体是一个周围被基于球面或椭球面的地表体单元包围的单位元,其高度基于椭球面或球面是一个常数(图 1)。
|
| 图 1 扇形柱体几何模型 Fig. 1 Geometry Model of the Tesseroid |
忽略地球曲率的影响,用球面扇形柱体近似椭球面扇形柱体。对于以地心为圆心,高度分别为H =0、H = h1的两个球面,其半径可分别近似表示为:r1=Rradii+0,r2=Rradii+h1,Rradii 表示所选等质圆的半径(一般是地球的平均半径)。则球面扇形柱体的重力位可表示为:
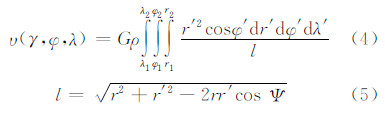
式中,l为计算点和积分点之间的距离;Ψ是点P和点Q之间的夹角:
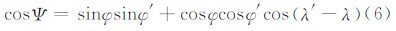
由于椭球积分困难,扇形柱体的重力位不能进行解析计算,但是可通过数值计算得到近似解,式(4)可以进行级数展开。通过计算得知,最有效的展开点是扇形柱体的几何中心点:
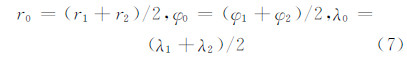
式(4)的积分核可展开为:
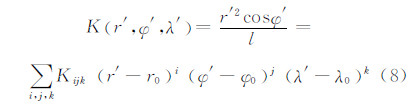
其中,
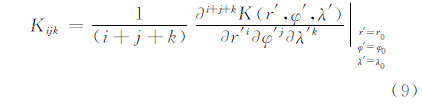
把式(8)代入式(4)并级数展开:
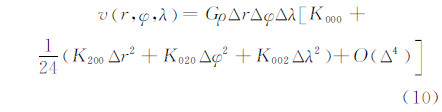
式中,Δr = r2-r1 = h2-h1,Δφ = φ2-φ1,Δλ = λ2-λ1。参数Kijk具体公式详见参考文献[11]。
1.3 Molodensky级数解的严密公式众所周知,Molodensky边值问题的界面——近似地形表面极不规则,故求解十分复杂,有众多学者对此作详细的研究[12]。顾及Molodensky三阶项影响的高程异常可表示为:
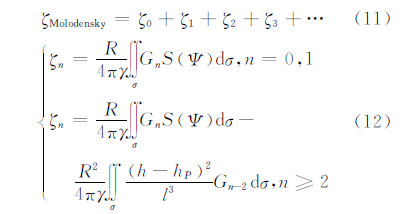
式中,S (Ψ) 是为以球面角距Ψ为变量的Stokes核函数:
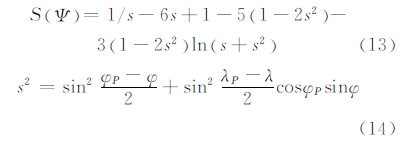
式(12)中,G0为空间异常;R为地球平均半径dσ为单位球面的面积元;γ为正常重力;Gn 由式(15)计算得到:
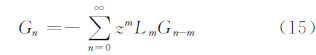
式中,Ln是奇异积分算子,可写成:
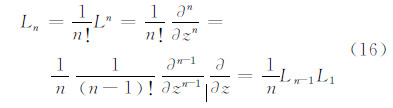
或
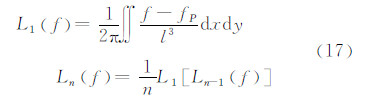
递推公式求解的关键在于奇异积分算子L1的计算:
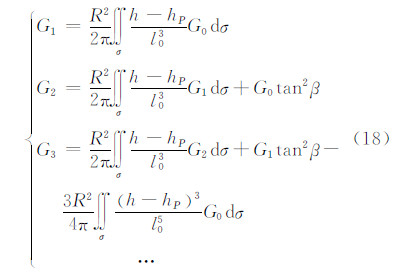
式中,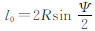 ,Ψ为计算点和流动点之间的球面夹角; h和hP分别为dσ和p点的高程; β 为地形倾角:
,Ψ为计算点和流动点之间的球面夹角; h和hP分别为dσ和p点的高程; β 为地形倾角:
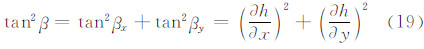
式(19)可由格网地形数值计算:
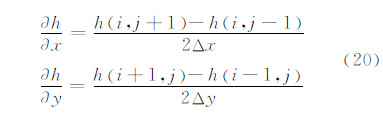
综合利用EGM2008重力场模型、GTOPO30地形资料及测高资料分析厘米级高程异常的地形影响。测试范围为我国陆地及近海区域的10°N~58°N、69°E~145° E范围。本文分别采用平面质量棱柱积分法、平面质量线积分法、球面质量棱柱积分法、椭球面扇形柱状积分法四种模型计算地形改正,比较不同积分单元和参考面对地形改正的影响;以Molodensky一阶项算法为依据,讨论Molodensky二阶项和三阶项对厘米级高程异常的影响;利用地形改正代替Molodensky级数解近似计算重力大地水准面,研究近似误差的影响。
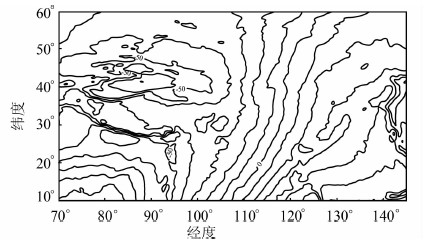
2.1 数据描述搜集研究区域内的GTOPO30和卫星测高数据。陆地上地形影响直接采用GTOPO30数据计算;海洋上地形影响采用Topex/Poseidon卫星测高数据减去EGM2008大地水准面高计算。采用EGM2008重力场模型计算重力异常及大地水准面高。EGM2008模型高程异常在我国大陆的总体精度为20 cm,模型空间异常在我国大陆的总体精度为10.5 mGal。图 2给出了由EGM2008重力位模型计算的大地水准面起伏。
|
| 图 2 由EGM2008重力位模型计算的大地 水准面起伏 Fig. 2 Geoid Undulations Calculated with EGM2008 Geopotential Coefficient Model |
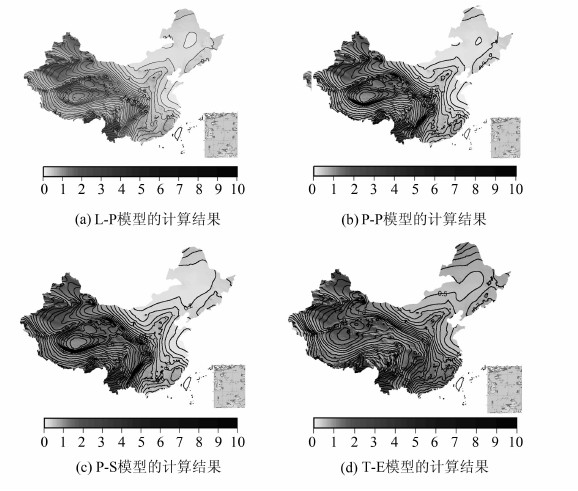
为了比较不同积分单元和不同参考面对地形改正计算的影响,本文分别采用平面质量棱柱积分法(P-P)、平面质量线积分法(L-P)、球面质量棱柱积分法(P-S)、椭球面扇形柱状积分法(T-E)4种模型计算地形改正。所有与地形影响有关的积分公式均采用2维FFT技术和100%填零计算,积分半径选取球面距离Ψmax= 5°。图 3给出了由4种模型计算的地形改正值。图 3(a)~3(c)计算中采用到的参数G=6.673·10-11m3 ·kg-1 ·s-2,ρ =2.67 g\5cm-3,R=6 378 137 m。图 3(d)计算中扇形柱体模型的边界设定为同心椭球半径r1 = R+hP 和 r2 = R+hij,椭球模型选用国际通用的GRS80椭球,其长半轴半径为 6 378 137.000 00 m;椭球短半轴半径为6 356 752.314 14 m,地壳密度取 2.67 g\5cm-3。表 1给出了4种模型计算的地形改正值的统计结果。
| /m | |||||
| 模型 | 最大值 | 最小值 | 平均值 | 均方差 | 标准差 |
| L-P | 6.24 | 0.00 | 0.65 | 1.17 | 0.97 |
| P-P | 6.83 | 0.00 | 0.70 | 1.26 | 1.05 |
| P-S | 9.05 | 0.00 | 0.75 | 1.33 | 1.11 |
| T-E | 9.46 | 0.01 | 1.01 | 1.62 | 1.22 |
|
| 图 3 采用不同质量单元计算的地形改正值 Fig. 3 Effect of Terrain Corrections on Height Anomalous Calculated by Different Mass Elements |
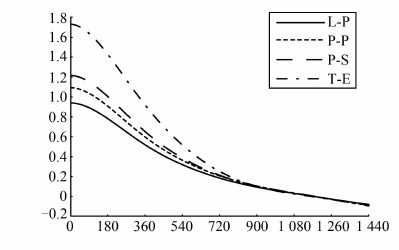
从表 1结果可以看出,椭球面扇形柱状积分法计算的地形改正值最大,球面质量棱柱积分法计算的地形改正值次之,平面质量线积分法计算的地形改正值最小。比较图 3四幅图可以看出,地形改正值与地形起伏有强相关性,且椭球面扇形柱状积分法计算的地形改正值较其他三幅图能更好地反映山区地形起伏的信息。为了进一步比较上述四种模型计算的地形改正的差异,图 4给出了地形对高程异常影响的协方差函数。从图 4可以清楚看出椭球面扇形柱状积分法计算地形改正在高频部分的优越性。因此,对于地形复杂区域的地形改正计算应优先选取椭球面扇形柱状积分法。
|
| 图 4 地形改正对高程异常影响的协方差函数 Fig. 4 Covariance Function in the Effect of Terrain Corrections on Height Anomaly |
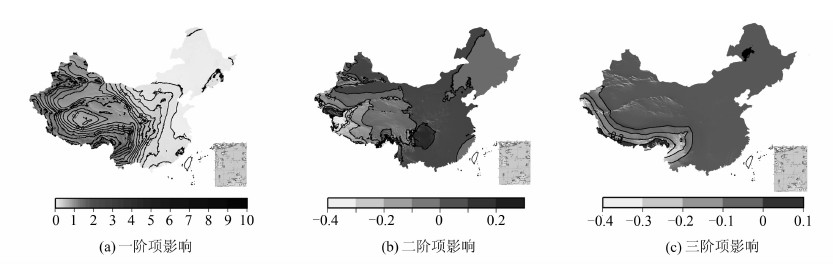
我国大地水准面计算工作中通常只考虑Molodensky一阶项,这里我们利用EGM2008重力场模型计算重力异常G0和大地水准面高ζ0,基于式(18)讨论二阶项和三阶项对厘米级高程异常的影响。计算中,积分半径选取Ψmax = 5°,积分公式均采用2维FFT技术计算。图 5给出了Molodensky一阶项至三阶项对高程异常的贡献。
|
| 图 5 Molodensky各项对高程异常的贡献 Fig. 5 The Effect of Molodensky Terms on Height Anomaly |
从图 5可以看出,一阶项对高程异常影响的大小与地形的起伏相关,其对高程异常贡献最大可达到10 m。二阶项在东部平原地区较小,但在中部和西部山区二阶项对高程异常的影响能达到分米级。鉴于目前厘米级大地水准面的任务,计算时必须顾及Molodensky二阶项的影响。三阶项影响在东部和中部都比较小,计算中可以忽略不计。然而在喜马拉雅地区三阶项影响可达到厘米级,故在计算青藏高原大地水准面时需考虑三阶项的影响。
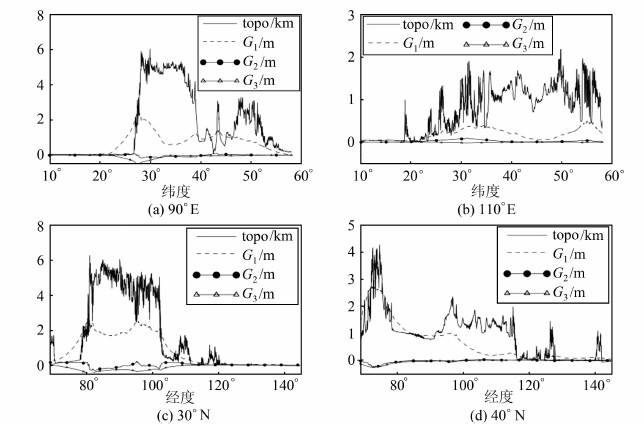
为了更直观地表现Molodensky各项对高程异常的影响,本文选取了4个剖面——90°E、110°E、30°N 和40°N,并给出了3个剖面处的一阶项至三阶项结果。由图 6结果可见,地形影响与高程大小没有明显的关系,而与高程起伏剧烈程度有关,比如图 6(a)中 28°N 和44°N,图 6(b)中34°N 和 54°N,图 6(c)中80°E、95°E处,图 6(d)中73°E处。故在地形变化较为复杂的地区应考虑二阶项甚至三阶项的影响。
|
| 图 6 一阶项至三阶项对高程异常影响的剖面图 Fig. 6 Profiles of Topography Height, Effects of G1 to G3 Terms on Height Anomaly Along Profiles |
我国目前计算重力大地水准面时,通常采用地形改正代替Molodensky 级数解近似计算。然而采用地形改正代替Molodensky级数解计算重力大地水准面的近似误差影响迄今未见研究,因此,本文将重点讨论利用地形改正代替Molodensky级数解计算重力大地水准面的近似误差影响。
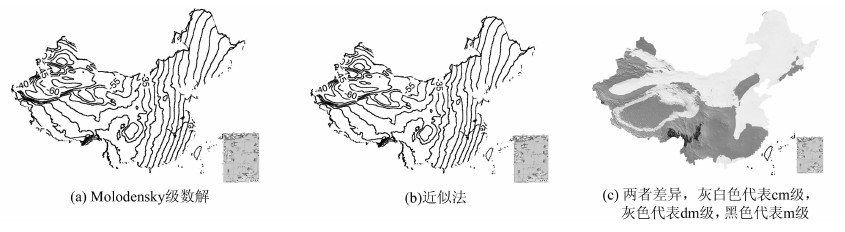
为了讨论两种方法近似误差的影响,分别采用Molodensky级数解法计算至三阶项及利用地形改正近似算法两种方法计算了中国大陆的重力大地水准面。图 7给出了两种方法计算的重力大地水准面模型,图 7(a)为由Molodensky算法计算的重力大地水准面,图 7(b)为利用地形改正的近似算法计算的重力大地水准面。图 7(c)给出了两种方法计算的大地水准面模型的差异,灰白色表示厘米级差异,灰色表示分米级差异,黑色表示米级差异。从图 7(c)结果可以看出两种方法计算的大地水准面差异与地形相关,在中国东部平原、内蒙古和塔里木盆地地区两者相差厘米级,而四川盆地、云南、贵州高原和西藏高原存在分米级差异,可见目前采用地形改正代替Molodensky级数解计算大地水准面的近似方法不适用于山区。
|
| 图 7 中国大陆重力大地水准面模型及差异 Fig. 7 Chinese Mainland Gravimetric Geoid Models and It’s Difference |
本文讨论了中国大陆厘米级高程异常的地形影响,推导了基于国际通用的GRS80椭球面采用扇形柱体计算地形改正的公式,给出了Molodensky一阶项至三阶项对高程异常贡献的严密级数展开式,并讨论了利用地形改正值代替Molodensky级数解计算重力大地水准面的近似误差影响。通过实际的算例分析,得出如下结论:
1) 分别利用平面质量线积分法、平面质量棱柱积分法、球面质量棱柱积分法、椭球面扇形柱状积分法计算地形改正值,结果表明四种模型得到的地形改正值在地形起伏大的地区差异较大,并且椭球面扇形柱状积分法计算的地形改正值包含了更多的地形起伏信息。因此在山区及地形起伏较大的地区应优先考虑椭球面扇形柱状积分法计算地形改正。
2) 基于Molodensky级数解算法,以Molodensky一阶项公式为依据,建立高阶项对高程异常影响的模型,给出Molodensky一阶项至三阶项对高程异常贡献的高精度算法。试验结果表明,一阶项对高程异常的影响与海拔高度没有明显的关系,而与地形的起伏剧烈程度有关;在丘陵和山区二阶项的影响达到分米级,故要使大地水准面达到厘米级精度,至少需顾及Molodensky二阶项的影响。
3) 利用地形改正代替Molodensky级数解计算重力大地水准面,研究不同地形起伏下的近似误差影响。试验结果表明,目前采用的利用地形改正近似算法在山区会导致分米级的误差。故利用地形改正代替Molodensky级数解计算大地水准面的近似算法,难以满足目前厘米级大地水准面精化的需求。
| [1] | Xu Houze. Some Problems on the Precise Determination of Regional Geoid in China[J]. Geospatial Information, 2006,4(5):1-3(许厚泽.我国精化大地水准面工作中若干问题的讨论[J].地理空间信息,2006,4(5):1-3) |
| [2] | Li Jiancheng.Study and Progress in Theories and Crucial Techniques of Modern Height Measurement in China[J]. Geomatics and Information Science of Wuhan University, 2007,32(11): 980-987(李建成.我国现代高程测定关键技术若干问题的研究及进展[J].武汉大学学报·信息科学版, 2007,32(11): 980-987) |
| [3] | Vacko M, Mojzeš M, Janák J, et al. Comparison of Two Different Solutions to Molodensky's G1 Term[J]. Studia Geophysica et Geodaetica, 2008,52(1): 71-86 |
| [4] | Guo Dongmei, Xu Houze. Research on the Singular Integral of Local Terrain Correction Computation[J]. Chinese Journal of Geophysics, 2011,54(2), doi:10.3969/j.issn.0001-5733.2011.04.012 |
| [5] | Kloch G, Krynski J . On the Determination of the Terrain Correction Using the Spherical Approach. International Association of Geodesy Symposia[J]. Gravity, Geoid and Earth Observation, 2010, 135 (1): 389-395 |
| [6] | Wild-Pfeiffer F,Heck B.Topographic and Isostatic Reductions for Use in Satellite Gravity Gradiometry[C].VIHotine-Marussi Symposium of Theoretical and Computational Geodesy: Challenge and Role of Modern Geodesy, Wuhan, 2006 |
| [7] | Heck B,Seitz K. A Comparison of the Tesseroid, Prism and Point-Mass Approaches for Mass Reductions in Gravity Field Modeling[J]. Journal of Geodesy, 2007,81:121-136 |
| [8] | Pellinen L P.On the Identity of Various Solutions of Molodensky's Problem with the Help of a Small Parameter[C]. International Symposium on Earth Gravity Models and Related Problems, Saint Louis, Missouri, 1972 |
| [9] | Forsberg R, Tscherning C C. Topographic Effects in Gravity Field Modelling for BVP[R]. Geodetic Boundary Value Problems in View of the One Centimetre Geoid, Lecture Notes in Earth Sciences, 1997 |
| [10] | Zhang Chuanyin, Chao Dingbo, Ding Jian,et al. Arithmetic and Characters Analysis of Terrain Effects for cm-order Precision Height Anomaly[J]. Acta Geodaetica et Cartographic Sainica, 2006, 35(4): 308-314(章传银,晁定波,丁剑,等.厘米级高程异常地形影响的算法及特征分析[J]. 测绘学报,2006, 35(4): 308-314) |
| [11] | Anderson E G. The Effect of Topography on Solutions of Stokes's Problem [R]. University of New South Wales, Kensington,1976 |
| [12] | Li Y C, Sideris M G. Improved Gravimetric Terrain Corrections[J]. Geophysical Journal of International, 1994,119: 740-752 |
 2016, Vol. 41
2016, Vol. 41


