文章信息
- 潘林, 蔡昌盛, 李施佳
- PAN Lin, CAI Changsheng, LI Shijia
- 北斗接收机初始相位偏差特性分析
- The Characteristics of BeiDou Receiver Initial Phase Bias
- 武汉大学学报·信息科学版, 2016, 41(3): 336-341
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 336-341
- http://dx.doi.org/10.13203/j.whugis20140112
-
文章历史
- 收稿日期: 2014-09-29

2. 武汉大学测绘学院, 湖北 武汉, 430079
2. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
利用IGS分析中心提供的精密轨道和精密钟差数据进行精密单点定位(PPP),静态观测可以得到cm级甚至mm级的定位精度,动态观测可以得到cm级到dm级的定位精度[1, 2]。但是在传统的PPP中,载波相位观测值中存在源自于接收机和卫星的初始相位偏差,这些初始相位偏差与整周模糊度难以分离[3],破坏了模糊度的整数特性,致使模糊度只能当作浮点数处理,导致PPP需要很长的收敛时间并且限制了PPP精度的进一步提高。精确估计出载波相位观测值中存在的初始相位偏差可以恢复模糊度的整数特性,从而正确固定模糊度,达到提高定位精度、缩短收敛时间的目的[4]。
目前,国内外学者已对卫星初始相位偏差的特性和估计方法进行了大量研究[3, 5, 6, 7, 8, 9, 10, 11],但在接收机初始相位偏差方面的研究报道却相对较少。Wang等人对GPS接收机的初始相位偏差特性进行了分析[10]。张小红等人推导了接收机端宽巷模糊度初始相位偏差的计算方法,并对其时变特性进行了分析[12]。分析接收机初始相位偏差的特性,对于非差整周模糊度的正确解算有重要的指导意义。本文利用组成零基线的两台北斗接收机所观测的数据,通过接收机间单差操作消除卫星的初始相位偏差以及其他误差,从而计算出接收机间单差的频率间接收机初始相位偏差,在此基础上对其特性进行了分析。
1 接收机初始相位偏差计算方法对于一个双频接收机,测码伪距和载波相位观测值可以表示如下[13]:
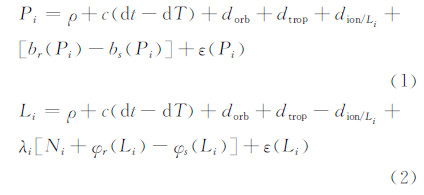
式中,i(i=1,2)表示卫星的两个频率;P是伪距观测值(m);L是载波相位观测值(m);ρ是卫星到测站之间的几何距离(m);c是光速(m/s);dt是接收机钟差(s);dT是卫星钟差(s);dorb是卫星轨道误差(m);dtrop是对流层延迟(m);dion是电离层延迟(m);br是接收机硬件延迟(m);bs是卫星硬件延迟(m);λ是载波相位观测值的波长(m/cycle);N是载波相位观测值上的整周模糊度(cycle);φr是接收机初始相位偏差(cycle);φs是卫星初始相位偏差(cycle);ε为观测噪声及多路径误差(m)。
由双频观测值得到MW (Melbourne-Wubbena)及GF(Geometry-Free)组合观测值,公式如下[14]:
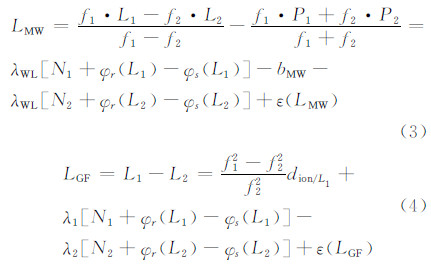
式中,f是载波相位观测值的频率(Hz);λWL是宽巷波长(m/cycle),λWL=c/(f1-f2);bMW是MW组合观测值中的硬件延迟(m),bMW={f1[br(P1)-bs(P1)] +f2[br(P2)-bs(P2)]}/(f1+f2)。
接收机间单差可以消除与卫星有关的误差,包括卫星初始相位偏差,这样就可以对接收机初始相位偏差进行估计。零基线试验中两台接收机共用一个天线,故使用零基线的数据进行接收机间单差还可以消除GF组合观测值中残留电离层误差的影响。MW和GF组合观测值的接收机间单差公式如下:
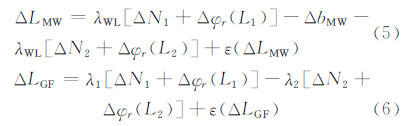
式中,ΔbMW是接收机间单差的MW组合观测值硬件延迟,ΔbMW= [f1Δbr(P1)+f2Δbr(P2)]/(f1+f2)。
若忽略噪声项的影响,由ΔLMW可以求得包含接收机初始相位偏差、接收机硬件延迟的单差宽巷模糊度,公式如下:

假设接收机初始相位偏差和硬件延迟对ΔNWL和ΔLGF观测值的影响非常小,联合式(6)和式(7)可以求得单差整周模糊度,公式如下:
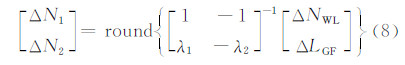
式中,round{·}表示四舍五入取整运算。
因为ΔLGF观测值中只含有整周模糊度项和接收机初始相位偏差项,在得到两个频率上的单差整周模糊度ΔN1与ΔN2之后,就可以利用式(9)计算出接收机间单差的频率间接收机初始相位偏差:
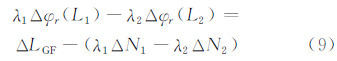
由式(8)计算出的ΔN1与ΔN2直接关系到接收机间单差的频率间接收机初始相位偏差求解,所以必须对ΔN1与ΔN2的正确性进行检验。由式(8)计算出ΔN1与ΔN2之后,可以求得双差整周模糊度:
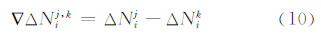
式中,j与k分别代表一颗北斗卫星,其中k代表参考卫星,并且满足j≠k。由式(10)得到的双差整周模糊度可以称之为“推导出的双差整周模糊度”,记做(▽ΔN)推。
利用零基线的观测数据直接进行双差操作可以消除除双差整周模糊度和观测噪声以外的其他所有项:

由式(11)、式(12)得到的双差整周模糊度可称为“计算出的双差整周模糊度”,记作(▽ΔN)计。利用该值可以验证获得的单差整周模糊度值是否正确。如果(▽ΔN)推与(▽ΔN)计相等,那么表明根据式(8)获得的ΔN1与ΔN2计算准确,这样就保证了根据式(9)计算的接收机间单差的频率间接收机初始相位偏差的正确性。
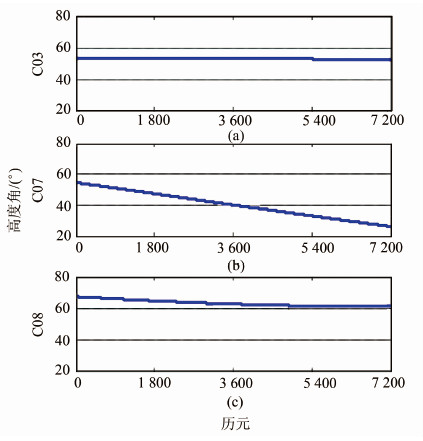
2 结果与分析选取司南K505型接收机2013-04-01所观测的北斗三频(B1、B2、B3)零基线数据进行分析,数据采样间隔是1 s。 选取C03、C07、C08三颗北斗卫星B1、B2上相同时间段的2 h观测数据进行分析,C03、C07、C08三颗北斗卫星的高度角如图 1所示。为了抑制观测噪声对求取接收机间单差的频率间接收机初始相位偏差的影响,所以选取卫星高度角较高的三颗北斗卫星进行分析。
|
| 图 1 C03、C07、C08三颗北斗卫星的高度角 Fig. 1 BeiDou Satellite Elevation Angles of C03, C07 and C08 |
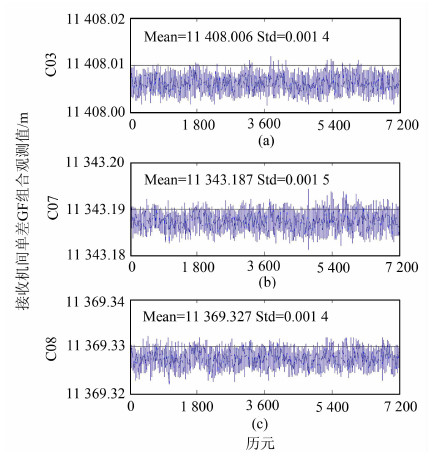
根据式(7)、式(6)计算出接收机间单差宽巷模糊度与GF组合观测值,根据式(8)计算出接收机间单差整周模糊度,根据式(9)求得接收机间单差的频率间接收机初始相位偏差。 图 2和图 3分别给出了C03、C07、C08三颗北斗卫星的接收机间单差宽巷模糊度与GF组合观测值。从图中可知,接收机间单差宽巷模糊度与GF组合观测值时间稳定性很好,为了进一步削弱噪声的影响,求取了接收机间单差宽巷模糊度与GF组合观测值的均值,然后将该均值带入到式(8)中,从而计算出接收机间单差整周模糊度,结果如表 1所示。在求取接收机间单差宽巷模糊度与GF组合观测值的均值之前,还需进行周跳探测与修复,本文使用TurboEdit方法[15]进行周跳探测和修复。

|
| 图 2 C03、C07、C08三颗北斗卫星的接收机 间单差宽巷模糊度 Fig. 2 Single-Difference-Between-Receivers Wide-Lane Ambiguities of BeiDou Satellites C03, C07 and C08 |
|
| 图 3 C03、C07、C08三颗北斗卫星的 接收机间单差GF组合观测值 Fig. 3 Single-Difference-Between-Receivers GF Carrier Phase Observations of BeiDou Satellites C03, C07 and C08 |
| C03 | C07 | C08 | |
| ΔN1 | -246 429 | -262 280 | -246 289 |
| ΔN2 | -236 490 | -248 486 | -236 226 |
| ▽ΔN1 | -140 | -15 991 | - |
| ▽ΔN2 | -264 | -12 260 | - |
为了对接收机间单差整周模糊度的正确性进行检验,需要验证(▽ΔN)推与(▽ΔN)计是否一致。根据式(10)可以得到(▽ΔN)推,由于C08高度角最高,所以选取C08为参考卫星,(▽ΔN)推计算结果如表 1所示。根据式(11)、式(12)可以得到(▽ΔN)计,同样选取C08为参考卫星,(▽ΔN)计计算结果如表 2所示。比较表 1和表 2可知,C03与C07卫星B1、B2上的(▽ΔN)计和(▽ΔN)推是一致的,这就表明求得的接收机间单差整周模糊度是正确的。
| ▽ΔN1 | ▽ΔN2 | |||
| Mean | Std | Mean | Std | |
| C03 | -140.000 | 0.005 | -264.000 | 0.004 |
| C07 | -15 991.001 | 0.005 | -12 260.001 | 0.004 |
在得到接收机间单差整周模糊度后,根据式(9)可求得接收机间单差的频率间接收机初始相位偏差,C03、C07、C08三颗北斗卫星B1、B2上的单差频率间相位偏差如图 4所示。图 4中红线表示小波去噪的结果,使用的小波基函数是sym4。从图 4中可知,三颗北斗卫星的单差频率间相位偏差均不在零附近变动,表明载波相位观测值中确实存在接收机初始相位偏差。与图 1对比可以发现,单差频率间相位偏差并不随卫星高度角变化而变化,表明其值具有较好的时间稳定性。为了检验三颗北斗卫星单差频率间相位偏差的变化趋势是否一致,特求取了小波去噪后三颗北斗卫星单差频率间相位偏差的相关系数,结果如表 3所示。由表 3可知,三颗北斗卫星的相关系数均在0.85以上,表明其变化趋势是一致的,并且从图 4中可知,三颗北斗卫星单差频率间相位偏差的均值相等,表明不同卫星相同频率组合上的单差频率间相位偏差一致。

|
| 图 4 C03、C07、C08三颗北斗卫星B1、B2上接 收机间单差的频率间接收机初始相位偏差 Fig. 4 Single-Difference-Between-Receivers Inter-Frequency Receiver Initial Phase Bias on B1and B2 of C03, C07 and C08 |
| B1- B2 | B1- B3 | |
| C03-C07 | 0.87 | 0.92 |
| C07-C08 | 0.86 | 0.92 |
| C03-C08 | 0.89 | 0.94 |
为了探究不同频率组合接收机间单差的频率间接收机初始相位偏差情况,求取了C03、C07、C08三颗北斗卫星B1、B3上的单差频率间相位偏差,结果如图 5所示。从图 5中可知,B1、B3上的单差频率间相位偏差和B1、B2相比,有0.025 m的偏差,并且B2(24.83 cm)与B3(23.63 cm)的波长相差不大,表明不同频率组合上的单差频率间相位偏差不同。由表 3中的相关系数可知,三颗北斗卫星B1、B3上的单差频率间相位偏差也是一致的。

|
| 图 5 C03、C07、C08三颗北斗卫星B1、B3上接收机间单差的频率间接收机初始相位偏差 Fig. 5 Single-Difference-Between-Receivers Inter-Frequency Receiver Initial Phase Bias on B1 and B3 of C03, C07 and C08 |
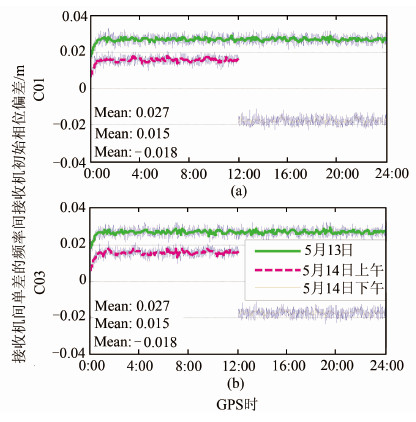
为了探究不同型号接收机的情况,选取Trimble NetR9型接收机2014-05-13、14日零基线数据进行分析,数据采样间隔是30 s。两天数据共分三组实验:5月13日,0:00接收机启动,24:00接收机关闭;5月14日上午,0:02接收机启动,12:00卫星信号输入电缆与信号分配器(splitter)断开连接,达到卫星信号完全失锁状态;5月14日下午,12:02卫星信号输入电缆与信号分配器重新连接,24:00接收机关闭。
图 6是三组数据中C01、C03两颗北斗卫星B1、B2上接收机间单差的频率间接收机初始相位偏差结果。图 6中蓝线表示原始结果,其他颜色线表示小波去噪结果。图 6中三组数据结果再次表明单差频率间相位偏差具有较好的时间稳定性。三组数据中,对于同一组数据,C01与C03卫星单差频率间相位偏差均值相等,两者的相关系数均在0.9以上,表明不同卫星相同频率组合上的单差频率间相位偏差一致。从5月13日与5月14日上午数据结果可知,接收机重启后,即接收机刚开始跟踪卫星时,单差频率间相位偏差有一个明显的收敛过程,需要约1 h收敛到稳定值。从5月13日与5月14日上午数据结果还可知,接收机重启后,单差频率间相位偏差发生明显偏移。从5月14日下午数据结果可知,卫星信号完全失锁后,单差频率间相位偏差同样发生明显偏移,但和接收机重启不同的是,并没有一个明显的收敛过程。结果表明,单差频率间相位偏差并不具有长期稳定性,接收机重新跟踪卫星后,其值会发生变化。
|
| 图 6 C01、C03两颗北斗卫星B1、B2上接收机间单差 的频率间接收机初始相位偏差 Fig. 6 Single-Difference-Between-Receivers Inter-Frequency Receiver Initial Phase Bias on B1 and B2of C01 and C03 |
本文利用组成零基线的两台北斗接收机所观测的数据,通过接收机间单差操作消除卫星的初始相位偏差,从而计算出接收机间单差的频率间接收机初始相位偏差。通过对北斗卫星B1、B2与B1、B3上单差频率间相位偏差分析,得出以下结论:单差频率间相位偏差具有短期稳定性,并不随卫星高度角变化而变化;接收机刚开始跟踪卫星时,单差频率间相位偏差需要一定的收敛时间才能达到稳定值;单差频率间相位偏差并不具有长期稳定性,接收机重新跟踪卫星后,其值会发生变化;接收机单差频率间相位偏差针对不同卫星在相同频率组合上是一致的。本文方法同样适用于GPS、Galileo等GNSS系统的接收机初始相位偏差分析。
| [1] | Zumberge J F, Heflin M B, Jefferson D C, et al. Precise Point Positioning for the Efficient and Robust Analysis of GPS Data from Large Networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5 005-5 017 |
| [2] | Gao Yang, Chen K. Performance Analysis of Precise Point Positioning Using Real-time Orbit and Clock Products[J]. Journal of Global Positioning Systems, 2004, 3(1/2): 95-100 |
| [3] | Ge Maorong, Gendt G, Rothacher M, et al. Resolution of GPS Carrier-phase Ambiguities in Precise Point Positioning (PPP) with Daily Observations[J]. Journal of Geodesy, 2008, 82(7): 389-399 |
| [4] | Ge Maorong, Chen J, Dousa J, et al. Development of the GFZ Real-time Precise Point Positioning Service[C]. EGU General Assembly 2011, Vienna, Austria, 2011 |
| [5] | Geng Jianghui, Teferle F N, Shi Chuang, et al. Ambiguity Resolution in Precise Point Positioning with Hourly Data[J]. GPS Solutions, 2009, 13(4): 263-270 |
| [6] | Zhang Xiaohong, Li Pan, Guo Fei. Ambiguity Resolution in Precise Point Positioning with Hourly Data for Global Single Receiver[J]. Advances in Space Research, 2013, 51(1): 153-161 |
| [7] | Li Xingxing, Zhang Xiaohong. Improving the Estimation of Uncalibrated Fractional Phase Offsets for PPP Ambiguity Resolution[J]. Journal of Navigation, 2012, 65(3): 513-529 |
| [8] | Laurichesse D, Mercier F, Berthias J P, et al. Integer Ambiguity Resolution on Undifferenced GPS Phase Measurements and Its Application to PPP and Satellite Precise Orbit Determination[J]. Journal of the Institute of Navigation, 2009, 56(2): 135-149 |
| [9] | Collin P. Isolating and Estimating Undifferenced GPS Integer Ambiguities[C]. Proceedings of ION National Technical Meeting, San Diego, USA, 2008 |
| [10] | Wang Min, Gao Yang. An Investigation on GPS Receiver Initial Phase Bias and Its Determination[C]. Proceedings of the 2007 National Technical Meeting of the Institute of Navigation, San Diego, USA, 2007 |
| [11] | Zhang Xiaohong, Li Pan, Zhu Feng. Estimation and Analysis for Widelane Carrier Phase Fractional Bias of Satellite[J]. Geomatics and Information Science of Wuhan University, 2012, 37(10): 1 177-1 180(张小红,李盼,朱锋. 卫星端宽巷载波相位小数偏差估计方法研究与结果分析[J]. 武汉大学学报·信息科学版,2012,37(10):1 177-1 180) |
| [12] | Zhang Xiaohong, Li Pan, Li Xingxing, et al. An Analysis of Time-varying Property of Widelane Carrier Phase Ambiguity Fractional Bias[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(6): 798-803 (张小红,李盼,李星星,等. 宽巷载波相位模糊度小数偏差时变特性分析[J]. 测绘学报,2013,42(6):798-803) |
| [13] | Cai Changsheng, Gao Yang. Modeling and Assessment of Combined GPS/GLONASS Precise Point Positioning[J]. GPS Solutions, 2012, 17(2): 223-236 |
| [14] | Cai Changsheng, Liu Zhizhao, Xia Pengfei, et al. Cycle-slip Detection and Repair for Undifferenced GPS Observations under High Ionospheric Activity[J]. GPS Solutions, 2012, 17(2): 247-260 |
| [15] | Blewitt G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199-202 |
 2016, Vol. 41
2016, Vol. 41



