文章信息
- 孙文, 吴晓平, 王庆宾, 周睿, 刘晓刚
- SUN Wen, WU Xiaoping, WANG Qingbin, ZHOU Rui, LIU Xiaogang
- 分形插值曲面及其在重力场格网加密中的应用
- Fractal Interpolating Curve Surface and Its Application in Gravity Anomaly Gridding Process
- 武汉大学学报·信息科学版, 2016, 41(3): 331-335
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 331-335
- http://dx.doi.org/10.13203/j.whugis20130492
-
文章历史
- 收稿日期: 2015-04-06

2. 信息工程大学地理空间信息学院, 河南 郑州, 450001;
3. 西安测绘研究所, 陕西 西安, 710054;
4. 地理信息工程国家重点实验室, 陕西 西安, 710054;
5. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉, 430079
2. Institute of Geospatial Information, Information Engineering Uniersity, Zhengzhou 450001, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
4. National Key Laboratory of Geo-Information Engineering, Xi'an 710054, China;
5. Key Laboratory of Geo-space Environment and Geodesy of Ministry of Education, Wuhan University, Wuhan 430079, China
重力场数据通常以按照经纬度划分的格网形式保存和使用,即以格网平均值及格网中心点坐标作为单个格网数据。如此,则引入了代表误差的概念,由亨特代表误差经验公式[1]可估计代表误差的大小:

式中,x、y分别表示经纬度方向的格网边长;E、C为代表误差及系数。由式(1) 可知,较高的分辨率对应较小的代表误差。故在重力辅助惯性导航中,通常将已有较低分辨率的重力异常源数据加密成为较高分辨率的格网数据,从而减小代表误差,降低误匹配概率,进一步提高匹配效能;同时,在某些数据较稀少的地区,要获得与数据密集地区相一致的数据分辨率,需要采用一定的加密算法来实现,上述两种需求可统一为规则格网重力场的加密处理过程。
重力异常数据的加密与格网化方法有多种[2, 3, 4, 5],主要包括Kriging插值法、Shepard插值法及其改进方法以及径向基函数法(radial basic function,RBF)等。众多学者对这些方法开展了卓有成效的研究,但这些研究主要集中于离散数据的格网化研究,较少涉及规则格网加密。此外,文献[6]将计算机构图中的孔斯曲面引入了导航用重力异常图重构,获得了较好的结果,进一步丰富了重力数据格网化和加密的方法。Kriging和Shepard插值法多用于离散数据的格网化处理,而在 规则格网加密过程中较少使用;RBF法关键在于基函数的选取,如样条法、二次曲面法等,在加密处理时使用较多。本文将分形插值曲面(fractal interpolating curve surface,FIC)理论引入重力异常的加密处理,将为相关研究提供有益参考。
1 分形插值曲面理论分形思想由Barnsley于1986年首先提出[7],强调自然界局部特征与整体的相似性,根据该思想发展出的分形插值曲线及曲面理论,为数据拟合与内插开辟了崭新的研究领域。
分形插值曲面的基本原理为[8]:对于给定的标准格网,设 I=[a,b],J=[c,d],D=I×J为数据的覆盖范围,经纬度方向格网分辨率分别为dB、dL,将区域划分为N×M个格网。对于每个格网中心点(Bi,Lj),其中a<Bi<b,c<Lj<d,其对应重力异常为Δgij。加密时,设每个格网内加密成n×m个格网。现欲构造分形曲面函数f,使得f(Bi,Lj)=Δgij,1≤i≤N,1≤j≤M。令纬度方向的压缩变换为:

经度方向的压缩变换为:

由整体与局部的相似性,压缩变换应满足如下条件:φi(B1)=BN-1,φi(Bn)=BN,λj(L1)=LM-1,λj(Ln)=LN,由此4个条件可解得:
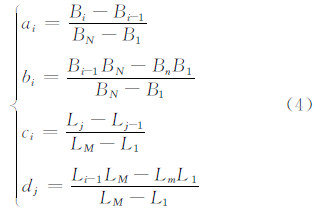
令函数f的压缩变换为:
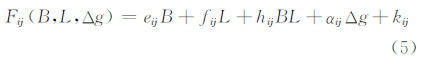
式中,0<αij<1为垂直比例因子,决定了分形曲面的维数即曲面的粗糙程度。插值后,原节点数据不变,故式(5)满足以下条件:

将原格网节点值代入式(6)并顾及式(2)~式(4),可解得式(5)中的系数为:

将系数代入式(5),即可求出加密后的格网重力异常值。
分形插值曲面模型的本质是将区域整体的变化趋势映射到局部区域,即格网中的重力异常变化趋势与整体的变化趋势相一致,从而实现内插加密过程。
2 RBF插值算法当应用于重力场格网化处理时,RBF插值算法可简单表示为:

式中,βij为未知系数;φ(rij)表示 基函数,以点间的距离为变量。求解时,选取适当的基函数,根据各个已知格网点之间的距离和实际重力异常值,求解未知系数,进而代入式(8)求解未知点的重力异常值,完成格网加密计算。因此,对于RBF算法来说,基函数的选取好坏是其计算精度的关键,常用的基函数有Gauss函数、Multi-Quadric函数等。文献[5]提出了一种基于Green函数的基函数,并将其成功应用于地球物理相关数据的处理中,得到较好效果。本文利用文献[9]提供的GMT软件实现了基于Green函数的径向基函数插值方法,其具体的理论推导见文献[5],限于篇幅,本文不再赘述。
3 算例分析 3.1 数据与实验本文实验采用数据为某地区5°×5°范围、分辨率为2′×2′的格网重力异常值,其数据统计特征:最大值为109.57 mGal,最小值为-52.23 mGal,平均值为1.83 mGal,标准差为16.84 mGal。
其具体实验设计为:分别采用FIC及RBF方法,将原始2′×2′数据加密为0.2′×0.2′格网数据。评定精度时,以原始格网点所在位置为中心、以1′为半径将加密后的半径区域内所有数据直接取平均,作为该原始格网点的插值结果,并与原始值作比较从而评价加密结果的精度。
3.2 结果与分析分别采用FIC及RBF法,对原始格网数据进行加密处理,得到的结果等值线图[9]及三维趋势图[10]分别如图 1、图 2所示(图中经纬度已经过处理,非真实坐标,下同),其中FIC中垂直比例因子通过多次实验设为0.01。

|
| 图 1 RBF插值结果三维趋势图 Fig. 1 3D Tendency Map of the RBF Method Result |

|
| 图 2 FIC插值结果三维趋势图 Fig. 2 3D Tendency Map of the FIC Method Result |
比较图 1、图 2的三维趋势图也可以明显看出,图 2中的三维趋势图相比图 1变化更为剧烈,尤其是图中方框部分区域。其原因在于FIC方法将整体趋势映射到局部,必然导致局部的值出现较大振荡。另外,垂直比例因子的正确选取与否和最终结果的精度有较大的关联。
3.3 基于完全布格异常的FIC插值为了解决上述局部误差过大的问题,利用基于“移去-恢复”思想进行插值。其具体方法是:利用地形数据求解完全布格异常,然后将完全布格异常作为原始数据进行插值,最后将插值结果恢复为空间异常。空间异常经过局部地形改正即为完全布格异常。相比空间异常,完全布格异常的变化趋势较为平缓,更加适合插值过程[6]。
局部地形改正的平面近似计算公式为[1]:

式中,Cp表示地形改正;fρ为引力常数与地壳平均密度的乘积;σ为积分区域;σ0为中央区;σ-σ0表示积分区域中中央区以外部分,称为近区,h、hp分别为流动点和计算点的高程。由于中央区存在奇异积分,故采用棱柱积分计算,而近区采用离散求和进行求解。
利用地形改正的计算结果,完全布格异常可由式(10)计算:
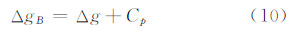
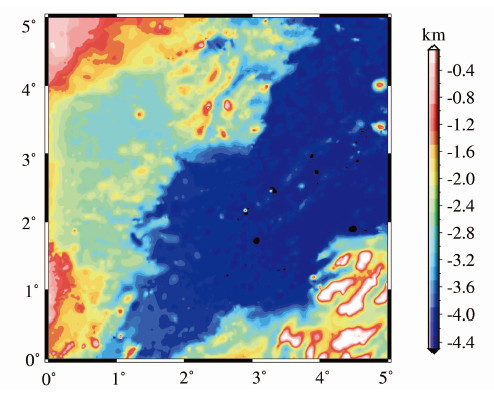
式中,ΔgB为完全布格异常;Δg为空间异常 。地形数据选择SRTM3数据[11],分辨率为3″×3″,高程标称精度±16 m。为了与实验格网分辨率相适应,采用直接取平均的方法处理2′×2′及0.2′×0.2′两种分辨率的地形图,0.2′×0.2′的等值线图如图 3所示。
|
| 图 3 地形示意图(0.2′×0.2′分辨率) Fig. 3 Contour Map of Terrain (0.2′×0.2′ Resolution) |
然后,分别利用式(9)计算两种分辨率的地形改正值,积分半径为60 km,中央区积分半径为5 km[12],利用式(10)将2′×2′分辨率的空间异常处理为完全布格异常,并作为插值的原始数据,即“移去”过程;插值完成后,利用式(10)将完全布格异常恢复成空间异常,即“恢复”过程。
基于“移去-恢复”法,利用FIC方法重新进行了插值加密处理(简称BAFIC),其三维趋势图如图 4所示。

|
| 图 4 BAFIC插值结果三维趋势图 Fig. 4 3D Tendency Map of the BAFIC Method Result |
其插值精度统计结果列于表 1。
| /mGal | ||||
| 方法 | 最大值 | 最小值 | 平均值 | 均方根 |
| RBF | 11.95 | -24.34 | -0.01 | 3.25 |
| FIC | 42.74 | -66.34 | -0.14 | 2.72 |
| BAFIC | 16.59 | -17.29 | -0.01 | 2.08 |
由表 1中的均方根项统计结果可以看出,FIC方法具有比RBF方法更高的精度;但同时需要注意的是,相比FIC方法,RBF方法的插值结果与真值的差值最大值、最小值、均值相比有优势;由表 1、图 2、图 4可以看出,基于完全布格异常的FIC插值法不仅在精度上有所提高,而且削弱了误差的最大值与最小值,极大地缩小了局部误差,使局部地区的重力异常在插值后的变化趋势仍然能够保持得较为平缓,这从三维趋势图中的方框部分区域可以明显看出。从频域的角度来说,地形起伏主要表现重力场信号的高频部分,移去地形部分影响后,完全布格异常信号能量主要集中于中低频部分,有利于内插和外推。
4 结 语本文出于规则格网重力异常加密及导航用重力异常图重构的需要,引入分形插值曲面理论,算例表明,在垂直比例因子正确的条件下,FIC具有比RBF更高的插值精度,但在局部地区的误差会出现较大起伏,这是由于分形曲面将整体映射到局部,从而使得局部与整体的趋势具有相似性,进而导致局部的起伏较大。为了解决这一问题,引入基于完全布格异常的FIC插值法,由于完全布格异常具有比空间异常更加平滑的空间特征,更加有利于内插和外推。算例结果也充分说明,相比FIC,基于完全布格异常的FIC插值法不仅精度有所提高,而且在局部地区的误差极值有较大降低,插值结果具有更高的可信度与实用性。另外,本文垂直比例因子通过多次试验得出,但在实际应用时如何正确高效地选取垂直比例因子,有待进一步深入研究。
| [1] | Lu Zhonglian. Theory and Method of the Earth's Gravity Field[M]. Beijing: People's Liberation Army Publishing House, 1996:217-218(陆仲连. 地球重力场理论与方法[M]. 北京: 解放军出版社, 1996: 217-218) |
| [2] | Wu Taiqi, Huang Motao, Ouyang Yongzhong, et al.The Study of High Precision Interpolation Technology in Marine Gravity Anomaly[J]. Science of Surveying and Mapping, 2008, 33(5): 70-72(吴太旗, 黄谟涛, 欧阳永忠, 等. 高精度海洋重力异常格网插值技术研究[J]. 测绘科学, 2008, 33(5): 70-72) |
| [3] | Liu Xiaogang, Wu Xiaoping, Wang Baojun, et al. Study on Gridding Methods of Satellite Gravity Gradient Data[J].Journal of Geodesy and Geodynamics, 2010, 30(6): 60-65(刘晓刚, 吴晓平, 王宝军, 等. 卫星重力梯度数据的网格化方法研究[J]. 大地测量与地球动力学, 2010, 30(6): 60-65) |
| [4] | Li Zhenhai, Wang Haihong.Comparison Among Methods for Gravity Data Gridding[J]. Journal of Geodesy and Geodynamics, 2010, 30(1): 140-144(李振海, 汪海洪. 重力数据网格化方法比较[J]. 大地测量与地球动力学, 2010, 30(1): 140-144) |
| [5] | Wessel P, Becker J M. Interpolation Using a Generalized Green's Function for a Spherical Surface Spline in Tension[J]. Geophys J Int, 2008, 174: 21-28 |
| [6] | Li Shanshan, Wu Xiaoping, Zhao Dongming. Coons Curved Surface Reconstruction Method of Marine Gravity Anomaly Map for Navigation[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(5): 508-515(李姗姗, 吴晓平, 赵东明. 导航用海洋重力异常图的孔斯曲面重构方法[J]. 测绘学报, 2010, 39(5): 508-515) |
| [7] | Barnsley M F, Demko S G. Iterated Function Systems and the Global Construction of Fractals[C]. Proceeding of the Royal Soc, London, 1986 |
| [8] | Xie Heping, Sun Hongquan.Theory and Application of Fractal Interpolating Curve[J]. Applied Mathematics and Mechanics, 1998, 19(4): 297-306(谢和平, 孙洪泉. 分形插值曲面理论及其应用[J]. 应用数学和力学, 1998, 19(4): 297-306) |
| [9] | Wessel P, Smith W H F. GMT Manual Pages[R]. School of Ocean and Earth Science and Technology, University of Hawaii at Manoa & NOAA, 2009 |
| [10] | Wang Jian, Bai Shibiao, Chen Ye.Geographic Information Mapping with Surfer 8[M]. Beijing: China Map Publishing House, 2004(王建, 白世彪, 陈晔. Surfer 8地理信息制图[M]. 北京: 中国地图出版社, 2004) |
| [11] | Chen Junyong.Quality Evaluation of Topographic Data from SRTM3 and GTOPO30[J]. Geomatics and Information Science of Wuhan University, 2005, 30(11): 941-944(陈俊勇. 对SRTM3和GTOPO30地形数据质量的评估[J]. 武汉大学学报·信息科学版, 2005, 30(11): 941-944) |
| [12] | Pang Zhenxing, Zhang Chuanding.Terrain Correction Computation by Controlling the Integral Radius Using the FFT Method[J]. Science of Surveying and Mapping, 2009, 34(4): 188-191(庞振兴, 张传定. 积分半径可控地形改正FFT算法的研究[J]. 测绘科学, 2009, 34(4): 188-191) |
 2016, Vol. 41
2016, Vol. 41


