文章信息
- 范磊, 钟世明, 李子申, 欧吉坤
- FAN Lei, ZHONG Shiming, LI Zishen, OU Jikun
- 跟踪站分布对非组合精密单点定位提取GPS卫星差分码偏差的影响
- Effect of Tracking Stations Distribution on the Estimation of Differential Code Biases by GPS Satellites Based on Uncombined Precise Point Positioning
- 武汉大学学报·信息科学版, 2016, 41(3): 316-321
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 316-321
- http://dx.doi.org/10.13203/j.whugis20140114
-
文章历史
- 收稿日期: 2015-02-10

2. 中国科学院测量与地球物理研究所大地测量与地球动力学国家重点实验室, 湖北 武汉, 430077;
3. 武汉大学卫星导航定位技术研究中心, 湖北 武汉, 430079;
4. 中国科学院光电研究院, 北京, 100094
2. State Key Laboratory of Geodesy and Earth's Dynamics, Institute of Geodesy and Geophysics, Chinese Academy of Sciences, Wuhan 430077, China;
3. GNSS Research Center, Wuhan University, Wuhan 430079, China;
4. Academy of Opto-Electronics, Chinese Academy of Sciences, Beijing 100094, China
差分码偏差(differential code bias,DCB)是发生在GPS卫星和接收机不同频率之间或相同频率不同码之间的硬件延迟偏差[1],其实质为不同码之间的时空参考点不同而导致的时间延迟差异[2],是GPS数据处理中不可忽略的误差项。DCB于卫星发射之前在地面实验室经过了标定,但随着卫星长期在轨运行,其值与初标定值并不相符,但在一定期间内保持得比较稳定[3]。因此,国内外很多学者和机构研究了卫星在轨期间DCB的估计方法,其中欧洲定轨中心(Center for Orbit Determination in Europe,CODE)和美国喷气推进实验室(Jet Propulsion Laboratory,JPL)通过全球200多个IGS(international GNSS service)跟踪站的相位平滑伪距观测值,利用全球单层电离层模型进行了DCB的精确估计[4, 5]。由于DCB的解算精度很大程度上取决于电离层建模精度[6, 7, 8],利用全球电离层模型必须保证足够多跟踪站的数据,而区域导航系统(如目前的BDS(BeiDou navigation satellite system))的跟踪站布设数量及分布范围均有限,无法利用CODE策略来估计DCB,鉴于此,近年发展起来的“IGGDCB(Institute of Geodesy and Geophysics DCB)两步法”利用区域电离层模型通过较少的跟踪站即可精确估计DCB[1]。
非组合精密单点定位有效利用了原始信息,规避了传统PPP(precise point positioning)消电离层组合观测值的噪声和多路径误差的放大效应,并能精确提取出包含站星方向上电离层斜延迟和DCB的组合电离层观测量[9],可用于GPS卫星DCB的精确确定。由于非组合PPP充分利用了相位数据,同时避免了平滑伪距电离层观测值易受平滑弧段长度和与跟踪站有关的误差影响,因而其电离层延迟的提取精度优于传统相位平滑码方法[10],具有很高的应用价值。
本文在已有研究的基础上提出了将非组合PPP与“IGGDCB两步法”相结合的卫星DCB提取新思路,充分吸收这两种方法的优点,并利用新方法重点探讨了跟踪站的不同分布和数量对DCB估计精度的影响,这对区域导航系统(如目前的BDS)的DCB估计具有一定的参考价值。
1 非组合精密单点定位提取组合电离层观测量非组合精密单点定位利用GPS双频伪距和相位观测值,其观测方程为:
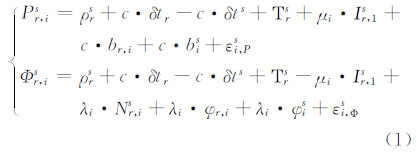
式中,s表示GPS卫星PRN号;r表示测站编号;i表示频率(i=1,2);Pr,is为测码伪距观测值;Φr,is为载波相位观测值;ρrs表示站星距;δtr为接收机钟差;δts表示卫星钟差;Τrs为站星方向上对流层斜延迟;μi表示与频率有关的常系数(μi=f12/fi2);Ιr,1s为站星方向上L1频点的电离层斜延迟;Νr,is为相关频率的模糊度参数;br,i和bis表示接收机端和卫星端硬件延迟的伪距偏差;φr,i和φis表示接收机端和卫星端对应的相位偏差;εi,Ps和εi,Φs包括多路径效应和观测值噪声。
IGS发布的卫星钟差产品是利用全球IGS跟踪站双频消电离层组合进行估计的,其并不等于实际的卫星钟差,而是包含了消电离层组合的差分码偏差项:
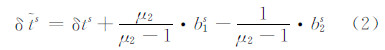
因此,若要利用IGS的钟差产品进行非组合PPP解算,需要对式(1)进行如下变换:
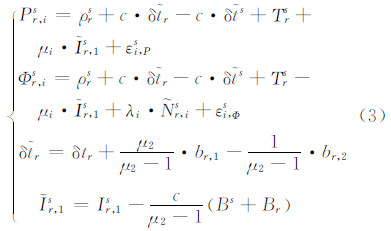
式中,Br=br,1-br,2和Bs=b1s-b2s分别表示接收机和卫星的差分码偏差,新的组合模糊度参数 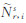 则包括了实际模糊度、相位偏差以及接收机和卫星差分码偏差。式(3)包含站星方向上电离层斜延迟以及接收机和卫星DCB的新电离层观测量
则包括了实际模糊度、相位偏差以及接收机和卫星差分码偏差。式(3)包含站星方向上电离层斜延迟以及接收机和卫星DCB的新电离层观测量 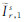 。这样,非组合PPP通过引入IGS的精密轨道和卫星钟差,估计跟踪站坐标、接收机钟差、天顶对流层延迟、组合电离层观测量和组合模糊度这5类参数。
。这样,非组合PPP通过引入IGS的精密轨道和卫星钟差,估计跟踪站坐标、接收机钟差、天顶对流层延迟、组合电离层观测量和组合模糊度这5类参数。
逐个利用各个跟踪站的组合电离层观测量进行区域电离层建模,将接收机和卫星DCB组合项与电离层斜延迟分离。考虑到区域建模,其模型选用三角级数函数模型[11, 12]:
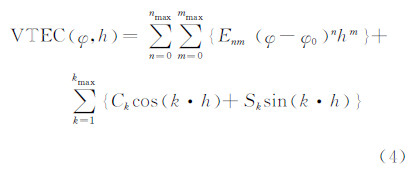
式中,φ为电离层穿刺点处的地磁纬度;φ0为接收机所在位置的地磁纬度;nmax、mmax与kmax分别表示多项式函数及三角级数函数的最大阶次,其取值大小取决于电离层活跃程度,考虑到实验期间电离层较活跃,参考文献[1]的设置,各项取值为nmax=mmax=2,kmax=5。Enm、Ck和Sk表示待估的模型系数,h为电离层穿刺点处与地方时相关的函数。经过区域电离层建模后,组合电离层观测量可表示为如下形式:
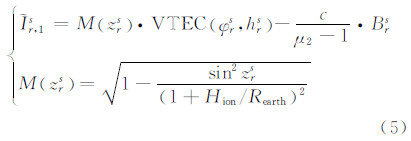
式中,Brs=Bs+Br;M(zrs)为用于将VTEC转换到站星方向上电离层总电子含量(STEC)的投影函数,其中zrs表示卫星的天顶距;Hion为电离层薄层的高度,本文选取为400 km;Rearth为地球的半径(km)。将 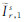 作为观测量,通过最小二乘即可求出每个跟踪站的Enm、Ck、Sk和Brs。
作为观测量,通过最小二乘即可求出每个跟踪站的Enm、Ck、Sk和Brs。
利用所有跟踪站估计出的Brs作为观测量进行接收机和卫星DCB的分离。由于接收机DCB与卫星DCB是线性相关的,其构造方程系数矩阵秩亏为1,因此,必须引入一个基准才能将接收机和卫星的DCB分离。本文采用所有可估卫星的DCB之和(重心基准)为零[5],可构造如下带有约束条件的观测方程:
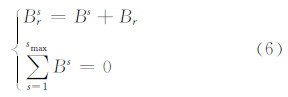
式中,smax表示可估计卫星的总数。
3 PPP误差改正及处理策略在非组合PPP中,首先采用MW组合和消电离层组合进行周跳探测和粗差剔除,同时对钟跳进行探测和修复。利用式(3)生成函数模型,并对天线相位中心、相位缠绕效应、相对论效应、地球自转效应以及固体潮和海洋负荷潮进行改正。对于部分只提供C1观测值而不提 供P1观测值的C1/P2型接收机还需要进行P1-C1偏 差的改正,采用CODE发布的P1-C1当月产品。为了解决PPP收敛过程中参数不稳定的问题,采用正反向平滑滤波进行数据处理。
4 实验分析 4.1 实验方案设计为了分析比较跟踪站分布和数量的不同对上述方法提取 GPS卫星DCB的影响,本文分别选取了欧洲区域和全球范围内的不同数量IGS跟踪站,利用2013年年积日255日~269日共15 d的实测数据进行处理,设计了表 1所示的4套方案。
| 方案1 | 方案2 | 方案3 | 方案4 | |
| 跟踪站分布 | 欧洲 | 欧洲 | 全球 | 全球 |
| 跟踪站总数量 | 6 | 20 | 6 | 24 |
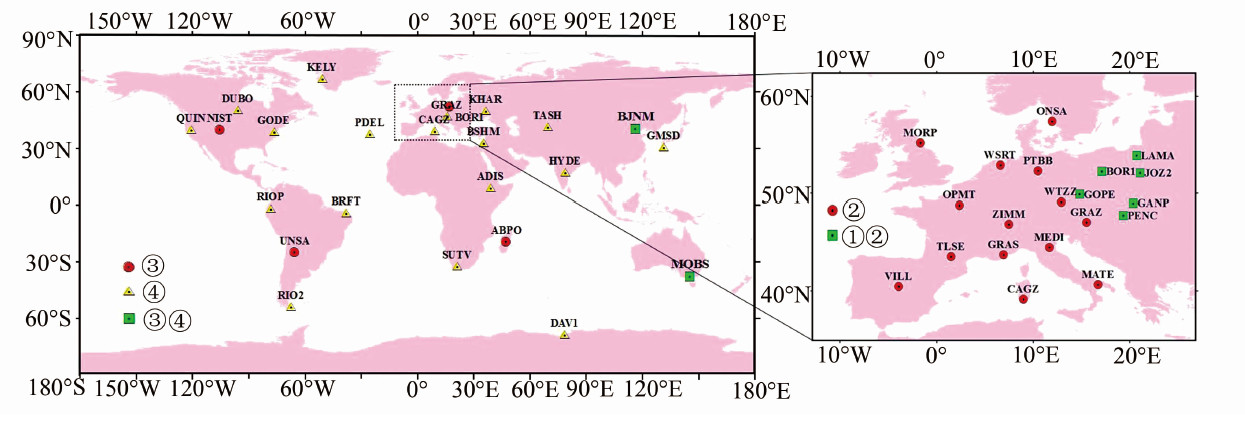
图 1显示了4种不同方案所选用跟踪站的分布。可以看出,方案1和方案2代表了跟踪站在欧洲集中分布条件下不同数量的情况,方案3和方案4代表了跟踪站全球均匀分布条件下不同数量的情况。
|
| 图 1 Distribution of Tracking Stations in Four Design Schemes Fig. 1 4种实验方案的跟踪站分布 |
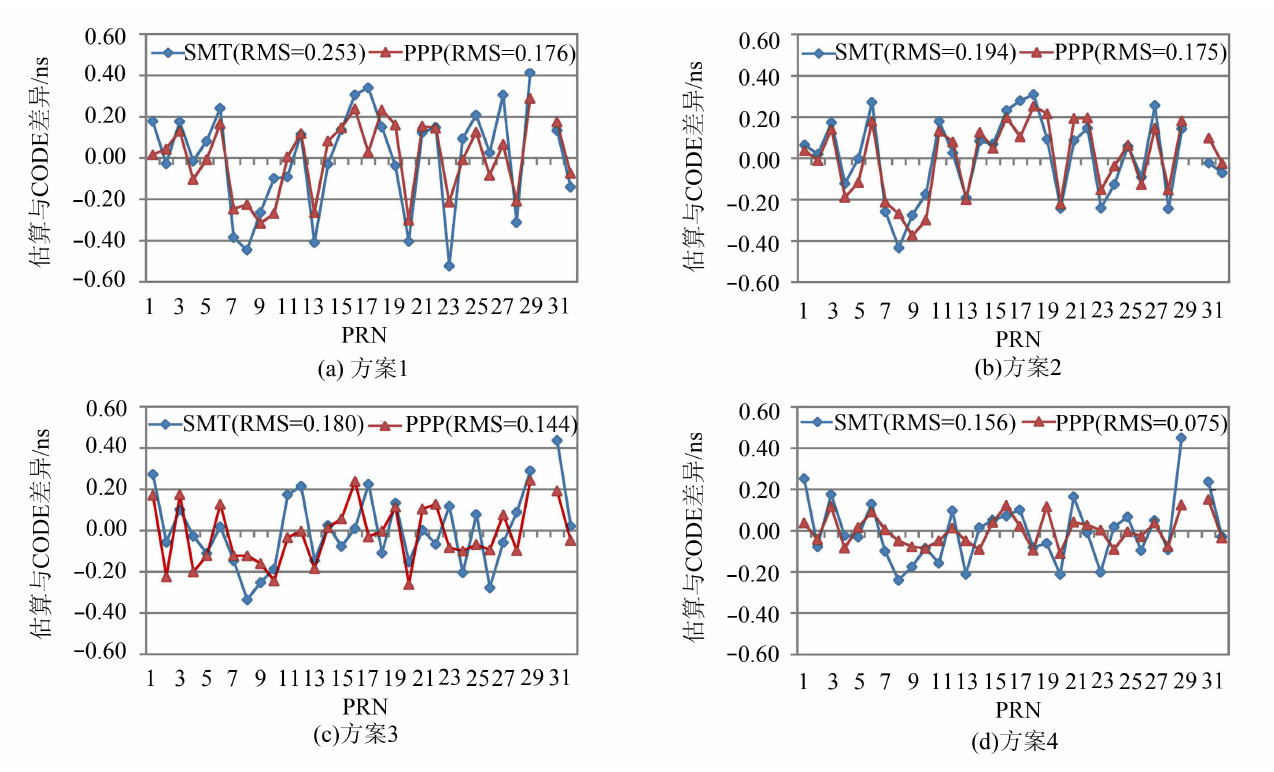
为了考察不同方案中卫星DCB估计的量值,实验将15 d各颗卫星单天解算的DCB取均值,并与CODE当月发布的DCB产品作差,结果如图 2。图中PPP表示非组合精密单点定位法提取DCB,SMT表示载波相位平滑码法提取DCB。需要说明的是,由于PRN30卫星在时段内不可用,实验采用的是剩下31颗卫星的重心基准,这样与CODE产生了由基准不一致导致的差异,因此,需要将CODE的产品转换至实验所采用的基准下,图 2是在统一基准下的结果。从图 2可以看出,利用本文提出的方法在4种方案中均能精确提取各颗GPS卫星的DCB,其RMS优于0.2 ns,并且在精度上优于载波相位平滑码方法。在本文方法中,方案1、方案2计算结果相当,其RMS均为0.18 ns,大部分卫星DCB在0.2 ns以内。相比方案1、方案2之间的差异,方案4较方案3在RMS上有明显的提高,其中方案4的RMS优于0.1 ns。考察4种方案可以发现,即使方案3比方案2所用跟踪站数目更少,DCB估计精度却更高,说明利用全球分布的跟踪站能得到更优的计算结果。
|
| 图 2 Difference Between Mean Value of Satellite DCB Estimates and CODE’s Monthly DCB Value in Four Schemes Fig. 2 4种方案卫星DCB均值与CODE月均值的差值 |
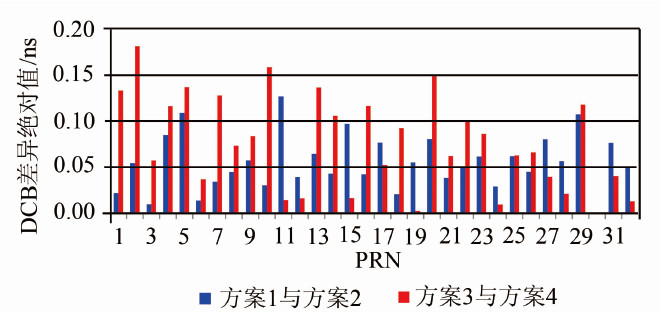
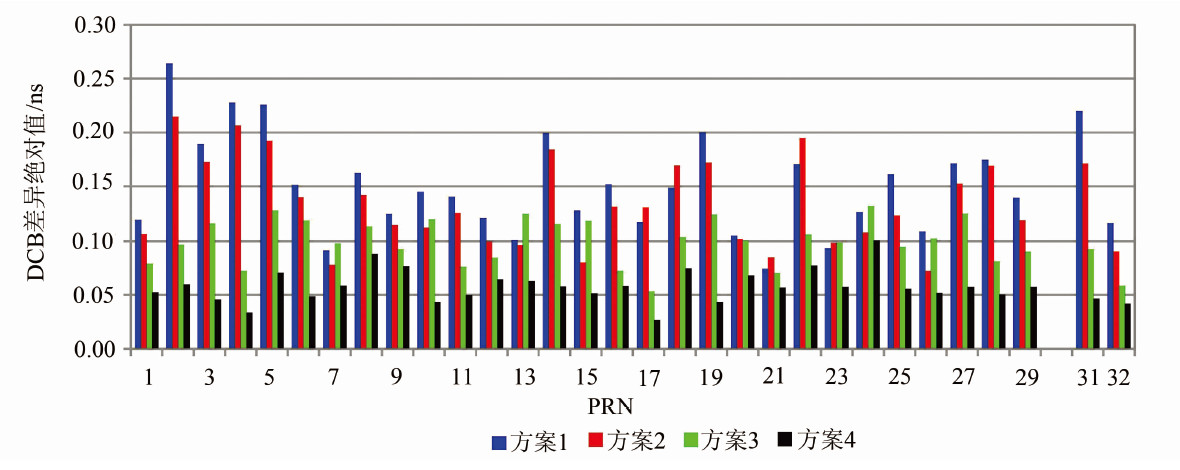
图 3显示了方案1、方案2之间与方案3、方案4之间卫星DCB均值差异的绝对值。从图 3中可以看出,方案1、方案2的范围为[0.01,0.13],其中除了PRN11卫星的差异达到了0.13 ns,其余卫星的差异均小于0.1 ns或在0.1 ns附近,这说明在区域集中分布的情况下,增加跟踪站的数量并不能显著提高DCB的估计精度。方案3、方案4的范围为[0.00,0.18],其中有11颗卫星的差异大于0.1 ns,这说明在全球分布情况下,增加跟踪站的数量能明显提高DCB的估计精度。这是因为区域布站时测站分布较密集,各站建模重叠范围较大,从而具有很强的相关性,这样实际上并没有减小建模误差,以上结果也表明仅增加观测样本对提高电离层建模精度贡献有限;对于较为分散的全球布站,一方面所有测站上空重叠范围较小,相关性较弱,这样建模精度较高的地区有利于“弥补”建模精度较低的地区,整体上减小了区域模型误差,从而提高了电离层整体建模精度;另一方面与CODE均采用全球布站建模,DCB估值的自洽性更好。
|
| 图 3 PPP法方案间卫星DCB差异的绝对值 Fig. 3 Absolute Value of the Difference by PPP Among Schemes |
为了考察各颗卫星DCB单天解的稳定性(天与天之间DCB估值的变化幅度),实验计算了15 d内每颗卫星DCB估值的标准偏差(STD),其结果如图 4。整体上来看,绝大部分STD统计量均优于0.2 ns。实验中,方案1的STD较方案2稍大,只有5颗卫星(PRN17、PRN18、PRN21、PRN22和PRN23)结果相反,这说明了在区域集中分布条件下增加跟踪站的数目可以改善DCB解的稳定性,原因是增加观测数据样本有利于提高电离层模型的拟合精度,从而提高DCB估值的稳定性。方案4与方案3相比,所有卫星的估计精度要高,说明在全球范围内增加跟踪站数目能显著改善了DCB解的稳定性。方案2和方案3相比,大多数卫星方案3的STD较方案2明显变小,但有7颗卫星方案3的STD较方案2稍大,这说明即使在跟踪站数量较少的情况下,全球布站仍有利于获得更高的稳定性,原因是全球布站有利于降低模型之间的相关性,从而整体上减小模型误差,使估值稳定性提高,然而数据样本数的减小在一定程度上削弱了模型的拟合精度而导致降低估值稳定性,因此最终结果是两者综合影响所致。从以上实验结果可以看出,模型相关性的影响更大。
|
| 图 4 PPP法四种方案各颗卫星DCB的稳定性 Fig. 4 The Day-to-day Variation of Satellite DCB Estimated by PPP in Four Schemes |
值得说明的是,由于实验所选取数据的年份正值太阳活动的高峰年,这直接影响到电离层的活跃度,因而在实验时间范围内区域电离层建模精度会受到很大的影响,实验结论相对较为保守。先前的研究表明,太阳活动峰年与谷年之间对卫星DCB的STD影响可以高达0.1 ns左右[1],由此看来,若在太阳活动的影响较小的年份,DCB估值会得到更高的精度。
5 结 语本文提出了利用非组合精密单点定位和“IGGDCB两步法”相结合的GPS卫星差分码偏差估计的新思路,并着重探究了跟踪站的分布对该方法估值的影响。设计了区域集中分布和全球均匀分布的不同数量的跟踪站的四种方案,通过15天的实测数据进行分析,发现利用上述方法在四种方案中均能精确提取卫星DCB,外符合精度上优于载波相位平滑码方法。本文经过进一步比较分析得出了以下结论:
1)区域分布条件下,增加跟踪站数量有利于提高DCB单天解稳定性,但对提高外符合精度贡献有限;
2)全球分布的跟踪站即使在数量较少的情况下依然优于区域数量较多跟踪站的外符合精度及单天解稳定性;
3)全球分布条件下,增加跟踪站数量能显著提高DCB估值的外符合精度及单天解稳定性,其数值均小于0.1 ns。
| [1] | Li Zishen, Yuan Yunbin, Li Hui, et al. Two-step Method for the Determination of the Differential Code Biases of COMPASS Satellites[J]. Journal of Geodesy, 2012,86(11):1 059-1 076 |
| [2] | Dai Wei, Jiao Wenhai, Jia Xiaolin. Application Research for Compass Navigation Satellite Interfrequency Bias Correction Terms[J]. Journal of Geomatics Science and Technology, 2009,26(5): 367-369(戴伟, 焦文海, 贾小林. Compass导航卫星频间偏差参数使用方法[J]. 测绘科学技术学报, 2009,26(5): 367-369) |
| [3] | Sardon E, Zarraoa N. Estimation of Total Electron Content Using GPS Data: How Stable are the Differential Satellite and Receiver Instrumental Biases[J]. Radio Science, 1997, 32(5): 1 899-1 910 |
| [4] | Komjathy A,Sparks L, Wilson B D, et al. Automated Daily Processing of more than 1 000 Ground-Based GPS Receivers for Studying Intense Ionospheric Storms[J]. Radio Science, 2005, 40(6):293-304 |
| [5] | Europe Center for Orbit Determination in Europe. CODE Analysis Strategy Summary[EB/OL]. http://igscb.igs.org/igscb/center/analysis/code.acn,2013 |
| [6] | Chang Qing, Zhang Donghe, Xiao Zuo, et al. A Method for Estimating GPS Instrumental Biases and Its Application in TEC Calculation[J]. Chinese Journal of Geophysics, 2001,44(5): 596-601(常青,张东和,萧佐,等. GPS系统硬件延迟估计方法及其在TEC计算中的应用[J]. 地球物理学报,2001, 44(5):596-601) |
| [7] | Brunini C, Azpilicueta F J. Accuracy Assessment of the GPS-based Slant Total Electron Content[J]. Journal of Geodesy, 2009, 83(8): 773-785 |
| [8] | Zhang Hongping, Shi Chuang, Tang Weiming. United Solution to Polynomial VTEC Modeling and DCB Analysis Using Ground-Based GPS Observations[J]. Geomatics and Information Science of Wuhan University, 2008,33(8): 805-809(章红平, 施闯, 唐卫明. 地基GPS区域电离层多项式模型与硬件延迟统一解算分析[J]. 武汉大学学报·信息科学版), 2008,33(8): 805-809) |
| [9] | Li Wei, Cheng Pengfei, Bei Jinzhong. Regional Ionosphere Delays' Calibration and Accuracy Assessment Based on Uncombined Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2011,36(10):1 200-1 203(李玮,程鹏飞,秘金钟.利用非组合精密单点定位提取区域电离层延迟及其精度评定[J]. 武汉大学学报·信息科学版,2011,36(10):1 200-1 203) |
| [10] | Zhang Baocheng, Ou Jikun, Yuan Yunbin,et al. Calibration of Slant Total Electron Content (sTEC) and Satellite-Receiver's Differential Code Biases (DCBs) with Uncombined Precise Point Positioning (PPP) Technique[J]. Acta Geodaetica et Cartographica Sinica, 2011,40(4): 447-453(张宝成, 欧吉坤, 袁运斌, 等. 利用非组合精密单点定位技术确定斜向电离层总电子含量和站星差分码偏差[J]. 测绘学报, 2011,40(4): 447-453) |
| [11] | Yuan Yunbin, Ou Jikun. A Generalized Trigonometric Series Function Model for Determining Ionospheric Delay[J]. Progress in Natural Science, 2004, 14(11): 1 010-1 014 |
| [12] | Liu Jingbin, Wang Zemin, Zhang Hongping, et al. Comparison and Consistency Research of Regional Ionospheric TEC Models Based on GPS Measurements[J]. Geomatics and Information Science of Wuhan University, 2008,33(5):479-483(柳景斌,王泽民,章红平,等.几种地基 GPS 区域电离层 TEC 建模方法的比较及其一致性研究[J]. 武汉大学学报·信息科学版,2008,33(5): 479-483) |
 2016, Vol. 41
2016, Vol. 41


