文章信息
- 范士杰, 陈冠旭, 刘焱雄, 牟春霖
- FAN Shijie, CHEN Guanxu, LIU Yanxiong, MU Chunlin
- 低高度角双频非差数据的周跳探测方法研究
- Cycle-Slip Detection Methods for Dual-frequency Un-difference Data at Low Elevation Angle
- 武汉大学学报·信息科学版, 2016, 41(3): 310-315
- Geomatics and Information Science of Wuhan University, 2016, 41(3): 310-315
- http://dx.doi.org/10.13203/j.whugis20140124
-
文章历史
- 收稿日期: 2014-11-25

2. 国家海洋局第一海洋研究所, 山东 青岛, 266061
2. The First Institute of Oceanography, State Oceanic Administration, Qingdao 266061, China
载波相位观测值的周跳探测与修复是高精度GPS定位数据处理的难点和关键。在精密单点定位(precise point positioning,PPP)中,双频非差观测数据的周跳探测尤为困难。目前,针对非差数据的周跳探测主要有电离层残差法[1]、MW组合法[2, 3]、TurboEdit方法[4]、LAMBDA方法[5]、TECR方法[6]。由于低高度角观测数据的测量噪声大,易受多路径效应影响等特点,采用上述算法进行周跳的探测时,容易出现误判或漏判的情况。电离层残差法可以准确地探测出小周跳,但是现有算法中固定而经验化的判定阈值影响了其探测效果,尤其是低高度角观测数据的周跳探测效果不甚理想;MW组合法在处理低高度角观测数据时,现有算法中的判定条件同样存在阈值计算不合理的情况。因此,本文基于电离层残差组合和MW组合,对低高度角双频非差数据的周跳探测算法进行改进。首先对电离层残差法中判定阈值的计算方法进行改进,引入时间窗口方法,利用周跳检测量的误差分布合理确定判定阈值的大小,从而克服经验阈值的局限性;然后对MW组合方法中的判定条件进行了改进,采用加权递推平滑和时间窗口相结合的方法进行宽巷模糊度的精确估计和精度评价,即采用高度角加权递推平滑的方法精确估计观测弧段宽巷模糊度的平滑值,同时利用时间窗口方法准确地估算宽巷模糊度值的中误差,由此确定更为合理的判定阈值。最后利用IGS站点观测数据进行了验证,改进算法取得了较好的周跳探测效果。
1 基于电离层残差组合的算法改进1985年Goad提出的电离层残差法是以历元间电离层残差相位组合的变化作为周跳检验量,取0.28周(cycle)为判定阈值。由于周跳检验量中包含电离层残差项,当发生电离层闪烁或异常跳变时,该方法可能会出现误判和漏判。此后的TurboEdit算法对此作了改进,将经过测码伪距修正的电离层残差组合在历元间的变化作为新的周跳检验量(式(1)),并以固定经验值6周作为判定阈值。但是过大的判定阈值大大降低了该算法的周跳探测效果,后来又将阈值改为0.28周和0.07周等固定经验值[7, 8, 9]。
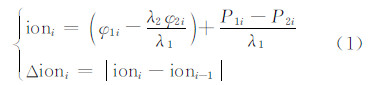
式中,ioni为第i历元经测码伪距修正的电离层残差组合;Δioni为第i历元的周跳检验量;φ1i和φ2i分别为第i历元L1、L2波段的载波相位观测值;P1i和P2i分别为第i历元L1、L2波段的测码伪距观测值;λ1和λ2分别为L1、L2波段的波长。
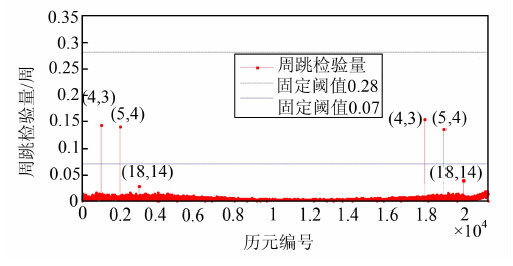
本文利用 IGS跟踪站shao的观测数据对上述算法进行验证,取PRN28卫星的一个完整观测时段(7 h左右),在低高度角观测历元加入模拟周跳(4,3)、(5,4)和(18,14),采用上述电离层残差法进行周跳探测的结果如图 1所示。由图 1可知,模拟周跳使检验量有明显跳动,但固定阈值0.28周不能判定出这3种周跳;固定阈值0.07周能够探测出周跳(4,3)和(5,4),却无法判定出周跳(18,14)。因此,过于经验化的判定阈值严重限制了电离层残差法的周跳探测能力。
|
| 图 1 原电离层残差法的周跳探测结果 Fig. 1 Cycle-Slip Detection Results of Original Ionosphere Residual Algorithm |
本文对上述算法进行了如下改进:仍将式(1)中的Δioni作为周跳检验量,在确定周跳的判定条件时,引入时间窗口方法,利用周跳检测量的误差分布合理确定判定阈值的大小,从而克服经验阈值的局限性。具体做法如下:选取时间窗口大小为k个历元,首先利用当前历元i之前k个历元的检验量数据求得其中误差σΔioni(式(2));然后利用式(3)进行判断,若式(3)中的两个不等式同时成立,则存在周跳;若第一个不等式成立,第二个不成立,则存在粗差。重复上述过程直至最后一个观测历元。
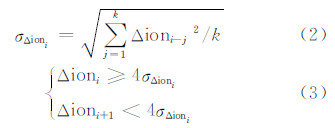
大量的实验表明,对于采样率为1 s的观测数据,时间窗口的长度k取值为120~480时的探测效果较好。本文k取 为300,即选用当前历元前300个历元作为一个窗口。对于不足一个时间窗口长度的观测数据,则仍然采用经验阈值进行周跳的判定。采用时间窗口的方式可以使周跳判定阈值能够与观测数据的噪声水平,特别是低高度角处较大的测量噪声相符合。时间窗口的长度过短,周跳判定阈值会受到未平滑的测量噪声影响,而出现频繁的不规则波动;时间窗口的长度过长,则会使与当前历元观测噪声相差较大的观测数据参与判定阈值的计算,两种情况均会降低周跳判定阈值的准确度,从而影响周跳探测的效果。
通过实验发现,时间窗口的长度超出建议的区间,误判率将会明显升高,且与建议区间的偏差越大,误判情况也就越严重。然而,已有文献关于时间窗口长度的建议不尽相同,作者以为这与所用实验数据的观测噪声不同有关。因此,建议利用部分观测数据作为样本,对算法进行训练,以误判率为标准确定合适的时间窗口长度范围。上述时间窗口法同样适用于不同采样率(如30 s、15 s等)观测数据的周跳探测,其时间窗口的长度须通过对样本数据的训练来进行相应地调整。另外,不同于以往基于时间窗口的算法,将多个未探测历元参与到同一时间窗口进行滑动,本文提出的改进算法采用逐历元滑动检测的方式进行周跳的探测,以避免一个时间窗口内出现多个周跳的情况,进一步提高周跳探测效果,增强周跳探测结果的可信度。
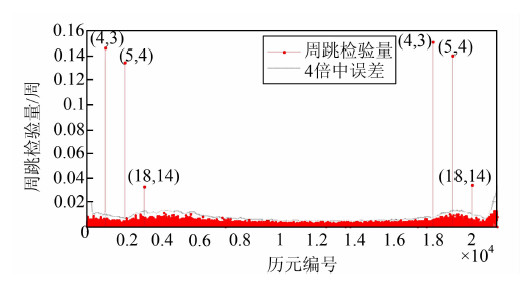
采用上述改进的电离层残差法对图 1中的数据重新进行周跳的探测,结果如图 2所示。从图 2中可以明显地看出:改进算法的判定阈值随着周跳检验量的观测质量而变化,与检验量的误差分布相一致,很好地克服了经验阈值的局限性,可以精确地探测出(4,3)、(5,4)和(18,14)等模拟周跳。
|
| 图 2 改进电离层残差法的周跳探测结果 Fig. 2 Cycle-Slip Detection Results of Improved Ionosphere Residual Algorithm |
1985年 Melbourne和Wubbena首次提出MW组合,1990年Blewitt将其用于探测GPS非差观测数据中的宽巷周跳,称为MW组合法。宽巷模糊度( NW)可由式(4)计算,实际应用中,利用式(5)进行NW平滑值和中误差的递推计算,周跳的判定条件为式(6)。
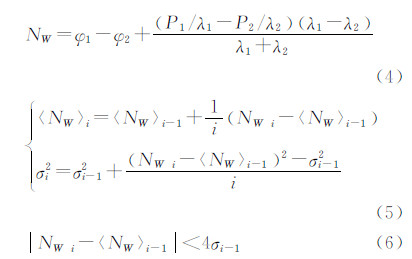
式中,〈NW〉i和σi分别为利用第i历元之前的全部数据等权递推计算得到的NW平滑值和中误差。
后来有学者引入时间窗口对上述算法进行了改进[10, 11],也就是将平滑值〈NW〉i的等权递推计算方式改为滑动平均,即首先选定一个适当的时间窗口大小m,然后利用当前历元i之前的m个历元的数据计算其平滑值,而不是利用该历元之前的全部数据。为便于描述,本文将上述改进方法称之为“时间窗口法”。
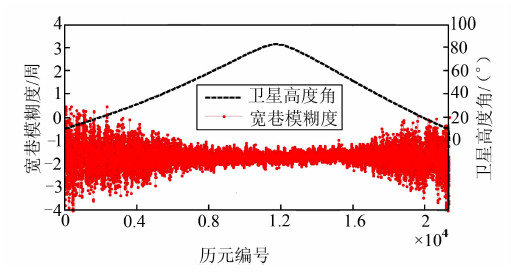
对于可视卫星的一个完整数据观测时段,若不存在周跳,则宽巷模糊度平滑值〈NW〉i的精度将不断提高,故“时间窗口法”的计算方式将人为地降低宽巷模糊度平滑值的精度。由图 3可以看出,单历元双频数据估算的宽巷模糊度值(NW)的精度随卫星高度角的大小而变化[12]。观测时段两端数据的卫星高度角较小,包括多路径误差在内的各项误差影响较大,进而导致NW估值的精度较低;而观测时段中间数据的卫星高度角较大,数据观测质量较好,NW估值的精度则较高。
|
| 图 3 宽巷模糊度和卫星高度角随 历元时间的变化 Fig. 3 The Variation of Wide Lane Ambiguity and Satellite Elevation Angle with Observation Epochs |
因此,本文仍然利用观测历元i之前的全部数据递推计算宽巷模糊度(NW)的平滑值,同时考虑不同卫星高度角的数据对平滑值计算的影响,采用卫星高度角的正弦函数确定相应历元MW组合观测值的权,并利用式(7)递推计算其加权平滑值(加权递推平滑),以保证宽巷模糊度平滑值的精确估计,为后续周跳判定阈值的合理确定打下良好的基础。
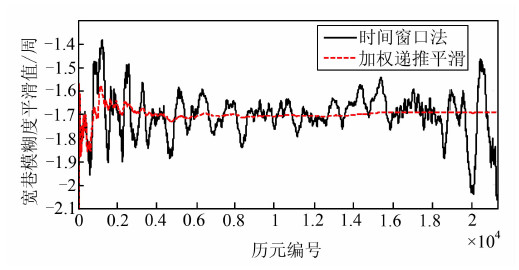
分别采用时间窗口法和加权递推平滑计算宽巷模糊度的平滑值,对比结果见图 4。从图 4中可以看出加权递推平滑可以得到更加稳定和准确的宽巷模糊度平滑值,而利用时间窗口法计算得到的宽巷模糊度平滑值的波动较大,仍然包含了较大测量噪声的影响,由此难以准确地估计宽巷模糊度值的精度,不利于后续周跳判定阈值的合理确定。随着卫星高度角的减小,在观测时段的尾部容易出现周跳误判的情况。
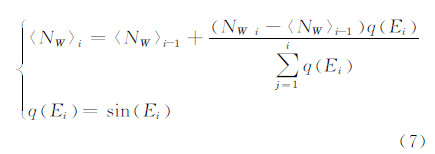
式中,Ei为第i历元的卫星高度角。
|
| 图 4 两种宽巷模糊度平滑值计算方法的结果对比 Fig. 4 The Comparison Between Two Results of Wide Lane Ambiguity from Different Computing Methods |
由图 3可知,观测时段中间和两端数据的观测质量不同,原MW组合算法利用当前历元之前的全部数据估算宽巷模糊度值的中误差,不能很好的反映其误差分布,从而导致其精度评价与实际情况不符。观测时段的中间历元递推计算中误差时,若用了之前全部历元数据,则会因质量较差的前端数据使中误差的计算值偏大,增加周跳探测的漏判率;对于时段尾部历元,若用了之前全部历元数据,则会因质量较好的中间数据使中误差的计算值偏小,增加周跳探测的误判率。故本文仍然采用时间窗口方法,选取时间窗口大小为m个历元,利用式(8)估算宽巷模糊度(NW)的中误差,由此确定更为合理的判定阈值,则周跳的判定条件见式(9)。其中,时间窗口大小m的取值与本文改进的电离层残差法的时间窗口取值一致。
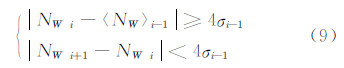
若式(9)中的两个不等式同时成立,则存在周跳;若第一个不等式成立,第二个不成立,则存在粗差。
综上所述,本文在原MW组合法和改进的时间窗口法的基础上,充分利用各自算法中的优点,提出了加权递推平滑与时间窗口相结合的MW组合周跳探测的新方法(本文称之为“改进的MW组合新方法”)。
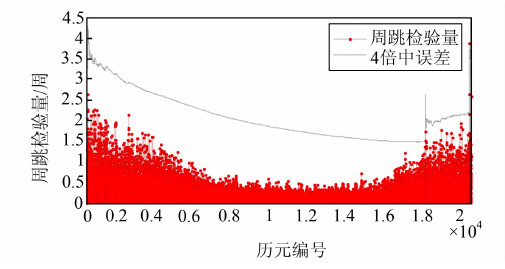
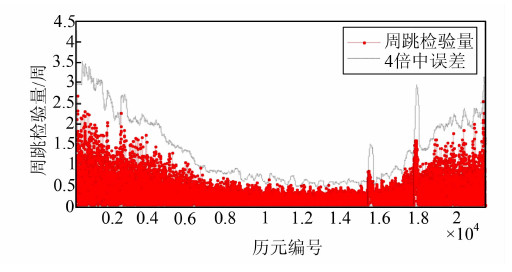
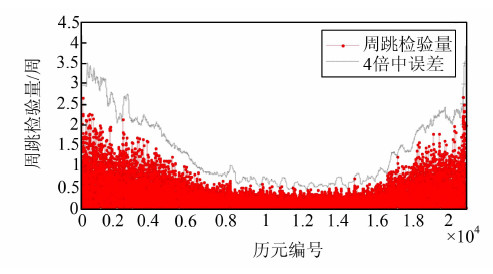
选取PRN28卫星的一个完整数据观测时段,分别采用原MW组合法、时间窗口法和改进的MW组合新方法进行周跳的探测,结果如图 5~图 7所示。从图 5可以看出,观测时段两端的周跳检验量的波动较大,而中间的波动较小,利用当前历元之前的全部数据进行精度评价与实际情况不符,时段中间历元计算的中误差偏大,时段尾部历元计算的中误差偏小,进而导致第18 745历元和21 167历元处出现周跳误判的情况。而从图 6和图 7中可以看出,时间窗口法和改进的MW组合新方法均利用时间窗口方式计算宽巷模糊度(NW)的周跳判定阈值(即四倍中误差),更好地反映了其误差分布,其周跳判定阈值有一定的吻合性,趋势一致,低高度角处对大于2~3周的宽巷周跳均保持着相似的探测敏感度。但是,时间窗口法于15 210和17 599历元处发生了周跳误判的情况。分析其原因可能是周跳检验量受到了低高度角处较大测量噪声的影响,造成了周跳误判的情况。从图 7可以看出,改进的MW组合新方法的探测结果没有出现误判现象。这是由于改进算法得到的宽巷模糊度平滑值更加精确,准确地估计了宽巷模糊度值的误差分布,从而确定了更加合理的周跳判定阈值,保证了周跳探测结果的准确性。
|
| 图 5 原MW组合法的周跳探测结果 Fig. 5 Cycle-Slip Detection Results of Original MW Combination Algorithm |
|
| 图 6 时间窗口法的周跳探测结果 Fig. 6 Cycle-Slip Detection Results of the Time Window Algorithm |
|
| 图 7 改进的MW组合新方法的周跳探测结果 Fig. 7 Cycle-Slip Detection Results of Improved MW Combination Algorithm |
为了验证本文改进算法的周跳探测效果,采用SHAO站2013年5月6日11:32:50.00~17:27:21.00采样率为1 s的“干净”数据进行试验。考虑到单一的电离层残差法和MW组合法的局限性,例如,电离层残差法对周跳组合(4,3)、(5,4)、(9,7)、(18,14)不敏感以及存在周跳(77,60)的探测盲区,而MW组合法则无法探测出两个频 率上出现相同周跳的情况。故本文在卫星高度角较低的观测时段两端数据中,按照以下3种方案添加模拟周跳:方案1为普通周跳组合;方案2为电离层残差法不敏感的周跳组合及其探测盲区周跳组合;方案3为MW组合法不能探测的周跳组合。
采用本文改进的电离层残差法和MW组合新方法,对上述低高度角双频非差观测数据进行周跳探测,结果汇总如表 1所示。表 1中Y/N表示电离层残差法探测成功,MW组合法探测失败;N/Y表示电离层残差法探测失败,MW组合法探测成功;Y/Y代表两种方法探测均成功;N/N代表两种方法探测均失败。
| 历元编号 | 卫星高度角/(°) | 方案1/周 | 探测结果 | 方案2/周 | 探测结果 | 方案3/周 | 探测结果 |
| 900 | 14.27 | (0,1) | Y/N | (4,3) | Y/N | (1,1) | Y/N |
| 1 900 | 19.29 | (2,0) | Y/N | (5,4) | Y/N | (2,2) | Y/N |
| 2 900 | 24.65 | (0,3) | Y/Y | (9,7) | Y/Y | (3,3) | Y/N |
| 3 900 | 30.37 | (4,0) | Y/Y | (18,14) | Y/Y | (4,4) | Y/N |
| 4 900 | 36.47 | (0,5) | Y/Y | (77,60) | N/Y | (5,5) | Y/N |
| 17 000 | 42.86 | (0,1) | Y/N | (4,3) | Y/N | (1,1) | Y/N |
| 18 000 | 34.58 | (2,0) | Y/N | (5,4) | Y/N | (2,2) | Y/N |
| 19 000 | 26.61 | (0,3) | Y/Y | (9,7) | N/Y | (3,3) | Y/N |
| 20 000 | 19.02 | (4,0) | Y/Y | (18,14) | Y/Y | (4,4) | Y/N |
| 21 000 | 11.86 | (0,5) | Y/Y | (77,60) | N/Y | (5,5) | Y/N |
对于方案1,改进的电离层残差法可以将普通周跳全部探测出来,而改进的MW组合新方法在低高度角时可以探测出两周以上的宽巷周跳。对于方案2,改进的电离层残差法在低高度角时可以将原来敏感度不高的周跳组合(4,3)、(5,4)和(18,14)探测出来,但是不能有效地将周跳(9,7)组合准确地探测出来;改进的MW组合新方法,在低高度角时仅有周跳组合(4,3)和(5,4)不能被探测出来。对于方案3,改进的电离层残差法,可以探测出全部的双频等周跳组合,弥补了MW组合法的缺陷。
通过以上3种不同方案的试验,验证了改进的电离层残差法和MW组合新方法在低高度角时的有效性,综合利用上述两种方法可以将模拟周跳全部探测出来。从探测结果可以看出,电离层残差法比MW组合法受观测数据质量的影响较小。因此,在实际应用中,建议采用以电离层残差法为主、MW组合法为辅的处理策略,能够得到更好的周跳探测效果。
但是,在方案1的试验中,我们发现MW组合法在低高度角时对2周以内的宽巷周跳有漏判风险,而此时若电离层残差法也不能探测出该类周跳(如周跳(9,7)),则该周跳组合在低高度角时可能会成为探测盲区。故笔者认为方案2中周跳(9,7)组合被探测出来带有一定的偶然性,可能与观测数据的质量有一定的关系。
4 结 语本文研究了已有文献较少关注的低高度角双频非差数据的周跳探测问题。首先对电离层残差法进行了改进,利用周跳检测量的误差分布合理确定判定阈值的大小,从而克服经验阈值的局限性;然后对MW组合法进行了改进,将原MW组合法和改进的时间窗口法进行了算法融合,提出了加权递推平滑与时间窗口相结合的新方法,以避免周跳误判或漏判的情况。最后,利用IGS跟踪站观测数据进行了算法验证,改进算法在低高度角时取得了较好的周跳探测结果,且算法思路简单,易于编程实现。但是,周跳(9,7)组合仍可能成为改进算法的探测盲区,这将是下一步研究重点。
| [1] | Goad C C. Precise Positioning with the GPS[M]. Berlin, Heidelberg:Springer,1987: 17-30 |
| [2] | Wu Jizhong, Shi Chuang, Fang Rongxin. Improving the Single Station Data Cycle Slip Detection Approach TurboEdit[J]. Geomatics and Information Science of Wuhan University, 2011, 36(1): 29-33(吴继忠,施闯,方荣新.TurboEdit单站GPS数据周跳探测方法的改进[J]. 武汉大学学报·信息科学版,2011,36(1): 29-33) |
| [3] | Zheng Zuoya. Study and Software Implementation of GPS Data Pre-processing and Onboard GPS Kinematic Orbit Determination[D]. Shanghai: Chinese Academy of Sciences (Shanghai Astronomical Observatory), 2005(郑作亚.GPS数据预处理和星载GPS运动学定轨研究及其软件实现[D]. 上海:中国科学院研究生院(上海天文台),2005) |
| [4] | Blewitt G. An Automatic Editing Algorithm for GPS Data[J]. Geophysical Research Letters, 1990, 17(3): 199-202 |
| [5] | Zhang Xiaohong, Li Xinxin. Instantaneous Re-Initialization in Real-time Kinematic PPP with Cycle Slip Fixing[J]. GPS Solutions, 2012, 16(3): 315-327 |
| [6] | Liu Zhizhao. A New Automated Cycle Slip Detection and Repair Method for a Single Dual-Frequency GPS Receiver[J]. Journal of Geodesy, 2011, 85(3): 171-183 |
| [7] | Yi Zhonghai, Zhu Jianjun, Chen Yongqi, et al. Cycle-Slip Detection and Correction Algorithm for Real-Time PPP[J]. Geomatics and Information Science of Wuhan University, 2011, 36(11): 1 314-1 319(易重海,朱建军,陈永奇,等. 实时精密单点定位中周跳探测与修复的算法研究[J]. 武汉大学学报·信息科学版,2011, 36(11): 1 314-1 319) |
| [8] | Zhang Shubi, Zhu Shaopan, Zhang Qiuzhao. A Combined Algorithm for Cycle Slips Detection and Correction[J]. Journal of Geomatics Science and Technology, 2012, 29(1): 1-4(张书毕,朱绍攀,张秋昭. 一种GPS周跳探测与修复的组合算法[J]. 测绘科学技术学报,2012,29(1): 1-4) |
| [9] | Zhang Xiaohong, Guo Fei, Li Pan, et al. Real-time Quality Control Procedure for GNSS Precise Point Positioning[J]. Geomatics and Information Science of Wuhan University, 2012, 37(8): 940-944(张小红,郭斐,李盼,等. GNSS 精密单点定位中的实时质量控制[J]. 武汉大学学报·信息科学版,2012,37(8): 940-944) |
| [10] | Cai Chongsheng, Liu Zhizhao, Xia Pengfei, et al. Cycle Slip Detection and Repair for Undifferenced GPS Observations Under High Ionospheric Activity[J]. GPS Solutions, 2013, 17(2): 247-260 |
| [11] | Yuan Yubin, Dang Yamin, Cheng Yingyan, et al. TurboEdit Algorithm and Its Improvements in Undifferentiated Phase Data Preprocessing[J]. Journal of Geodesy and Geodynamics, 2009, 29(3): 109-113(袁玉斌,党亚民,成英燕,等. 非差相位数据预处理的TurboEdit算法及其改进[J]. 大地测量与地球动力学,2009,29(3): 109-113) |
| [12] | Miao Ying, Sun Zhaowei, Wu Shunan. Error Analysis and Cycle-Slip Detection Research on Satellite-Borne GPS Observation[J]. Journal of Aerospace Engineering, 2010, 24(1): 95-101 |
 2016, Vol. 41
2016, Vol. 41


