文章信息
- 舒宝, 刘晖, 张明, 吴丹
- SHU Bao, LIU Hui, ZHANG Ming, WU Dan
- 北斗系统硬件延迟解算及精度分析
- Evaluation and Analysis of BDS Instrumental Biases
- 武汉大学学报·信息科学版, 2016, 41(2): 279-284
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 279-284
- http://dx.doi.org/10.13203/j.whugis20140058
-
文章历史
- 收稿日期: 2014-05-29

2. 长安大学地质工程与测绘学院, 陕西西安, 710054
2. School of Geology Engineering and Geomatics, Changan University, Xi'an 710054, China
北斗卫星导航系统(BeiDou Satellite Navigation System,BDS)是中国正在实施的自主发展的全球卫星导航系统,近年来,北斗卫星系统得到迅猛发展,目前在轨卫星已达14颗,已具备在亚太大部分地区提供卫星导航服务的能力。随着系统进一步发展,北斗服务系统将发布中国区域的电离层产品。目前国际上最权威的电离层产品是由国际GNSS服务组织(International GNSS service,IGS)电离层小组提供,IGS电离层小组旨在提供全球高精度电离层图以及GNSS卫星和各个监测站的DCB参数。研究表明,利用GNSS观测数据解算电离层总电子含量的最大误差源是卫星和接收机的硬件延迟[1, 8],此外硬件延迟是影响导航定位和授时精度的重要因素。硬件延迟通常和电离层模型系数同时解算[2, 4, 5],我国的一些学者基于GPS数据对GPS卫星的DCB参数进行了一系列的研究,解算结果和IGS发布的结果差异为亚纳秒级[1]。由于北斗系统卫星分布情况以及跟踪站数量的限制,文献[3, 6, 10]采用IGS发布的电离层产品,联合双频无几何距离观测数据采用最小二乘的方法解算卫星和接收机的硬件延迟,精度为1 ns左右,李子申提出用附近站GPS卫星观测的电离层延迟信息辅助北斗卫星硬件延迟的解算[9],精度较好,但这些方法都在一定程度上依赖于电离层延迟先验信息的精度。
本文采用IGS电离层小组的模型求解方法,联合中国区域北斗和GPS卫星观测数据,用球谐函数模型采取多站求解的方式来获取北斗卫星的硬件延迟。采用该策略一方面是为了弥补电离层建模时北斗卫星星座的分布问题,提供均匀分布的观测数据,另一方面可以提高电离层和DCB的解算精度。最后通过多天数据的解算,对北斗卫星DCB的稳定性作出了评价。
1 硬件延迟的估算方法 1.1 观测数据的处理利用双频观测值不但可确定不同频率的观测值所受到的电离层延迟进而消除其影响,而且可测定穿刺点(卫星信号传播路径与中心电离层的交点)上总电子含量(total electron content,TEC)值。

式(1)、式(2)是原始伪距和载波相位观测值的表达式,仅考虑因频率不同而引起的弥散误差。其中,m=1,2分别代表北斗卫星和GPS卫星信号的频段;ρ是卫星和接收机间的几何距离;Bms 、Bmr是对应频段的卫星和接收机的硬件延迟。利用式(1)、式(2)得TEC的计算公式:

式中,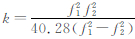 ,f1、f2分别对应北斗B1、B2和GPS卫星的L1、L2的频率。由于载波中有模糊度参数,一般采用伪距观测值建模,为了提高伪距的精度,在周跳探测后,本文采用模糊度平滑伪距的方法对伪距进行平滑:
,f1、f2分别对应北斗B1、B2和GPS卫星的L1、L2的频率。由于载波中有模糊度参数,一般采用伪距观测值建模,为了提高伪距的精度,在周跳探测后,本文采用模糊度平滑伪距的方法对伪距进行平滑:
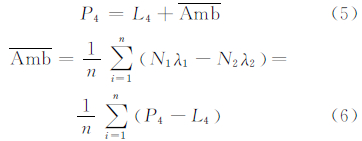
式中,P4=P2-P1;L4=L1-L2。
因此式(3)可以写为:
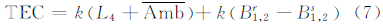
通过卫星和接收机的坐标以及单层球壳模型的高度就可以算出穿刺点的经纬度,以及穿刺点处的天顶距z′和电离层映射函数,在高度角大于15°~20°时各类映射函数计算的效果并无大的差异[4, 7],本文采用CODE的三角函数单层模型映射函数[7]:
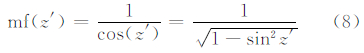
式中,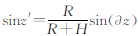 ;R为地球半径;H为单层模型的高度;z为测站卫星天顶角;∂=0.978 2。
;R为地球半径;H为单层模型的高度;z为测站卫星天顶角;∂=0.978 2。
常用的电离层模型有多项式、三角级数、低阶球谐函数模型等。三角级数模型在局部区域能够有效的模拟长时段的电离层延迟,但其仅仅是数学上的拟合,得到的三角级数系数没有真正代表电离层周日变化的特性,且三角级数采用的基函数不完全是三角级数,而是加入了纬度地方时的线性组合,不满足正交条件,精度相对较差[4]。本文采用低阶球谐函数和多项式模型利用中国区域的多个观测站求解北斗和GPS卫星的硬件延迟。采用该策略可以相互验证模型的精度,排除因模型的选取的不同而引起的硬件延迟的解算精度偏差。下面介绍多项式和低阶球谐函数模型。
电离层多项式展开模型是将垂直总电子含量(vertical total electron content ,VTEC)看作是纬度差 φ-φ0和太阳时角差S-S0的函数。其具体表达式为:
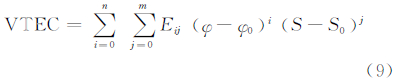
式中,φ0为测区中心点的地理纬度;S0为测区中心点(φ0,λ0)在该时段中央时刻t0的太阳时角;S-S0=(λ-λ0)-(t-t0),λ为信号路径与单层的交点的地理纬度,t为观测时刻。
低阶球谐函数模型是在太阳-地球坐标框架中来模型化穿刺点的电离层延迟,可以达到类似于广域差分系统(WAAS)格网电离层模型精度的精度。这里,在太阳方向固定的地磁坐标系中,具体形式如下:
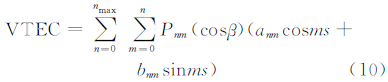
式中,anm、bnm为待估系数;Pnm(cosβ)为缔合勒让德函数;s为过穿刺点经线与过地心-太阳连线的经线之间的夹角;β为地磁纬度。将式(7)、式(8)式代入式(9)、式(10)得:

多项式模型选取p×q阶,低阶球谐函数的阶数取m阶。本文联合中国区域的GPS和北斗观测值进行电离层建模时,每次处理一天的数据,时段长度取为2 h,则两模型求解的参数分别是:

式中,NGsite、NCsite分别为GPS和北斗测站总数;NGsat、NCsat分别为观测到的 GPS、北斗系统的卫星总数。
从式(11)、式(12)可以看出测站和卫星的硬件延迟偏差无法分离,GPS 求解硬件延迟的约束条件是所有卫星的DCB参数和为零。这是一种重心基准的方法,不会对电离层模型参数造成任何影响,只是对接收机和卫星的硬件延迟带来了一个未知的常数偏差,在实际运用中只是卫星DCB的相对值影响用户定位的精度,因此参考基准的变化并不影响DCB本身的解算精度[7]。在中国大部分区域,一天的观测数据北斗卫星是全部可见的,为了便于评价本文所用方法计算的北斗系统DCB的精度,需要提供一个相对稳定的基准即可,北斗系统采用和GPS卫星同样的约束:
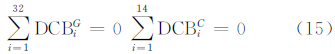
为了保证全天时段及空域的连续性,在测区中心上空选取5°×5°的格网,在选取的格网点和时段结点处构造总电子含量相等的条件[4]:

式中,(bg,lg)为格网点地理坐标;t为时段连接点;i为一天内第i个时段。
北斗系统和GPS组合时,观测值定权采用赫尔墨特方差分量估计[12],根据GPS卫星、北斗GEO、IGSO、MEO卫星用四类观测值残差平方和不断迭代重新定权,直到各类观测值的单位权方差基本相等。
2 数据处理及分析 2.1 数据来源及模型精度验证目前北斗系统在轨卫星有5颗GEO卫星,5颗IGSO卫星,4颗MEO卫星,卫星类型及分布不利于电离层建模,仅采用北斗系统求解中国区域的电离层模型及卫星和测站的硬件延迟是不可行的,另一方面现有的北斗系统跟踪站较少,且分布不均匀,因此本文通过联合GPS和北斗系统观测数据一起求解的方式来改善卫星的空间分布及测站分布从而提高北斗卫星的解算精度。图 1是中国区域(国界数据来源:国家地理信息局)及周围的测站分布情况,其中圆点表示仅有GPS观测值,三角点表示同时观测GPS和BDS。图 2是这些站上空穿刺点分布图,其中绿色点的是GPS卫星与测站的穿刺点分布,红色点的是北斗GEO卫星的穿刺点,蓝色点的是北斗IGSO卫星的穿刺点,黑色点的是北斗MEO卫星的穿刺点分布。从图中可以看出仅有北斗卫星时,穿刺点的分布较差,联合GPS观测值后,穿刺点分布情况有了很大改善。

|
| 图 1 所选测站分布图 Fig. 1 Distribution of Selected Stations |

|
| 图 2 测站上空穿刺点分布图 Fig. 2 The Puncture Points Map Over the Slected Stations |
在区域模型电离层建模中,DCB的解算精度与测站数量及分布,卫星空间几何分布因素密切相关,模型及相关参数的正确选取对电离层的解算精度至关重要。
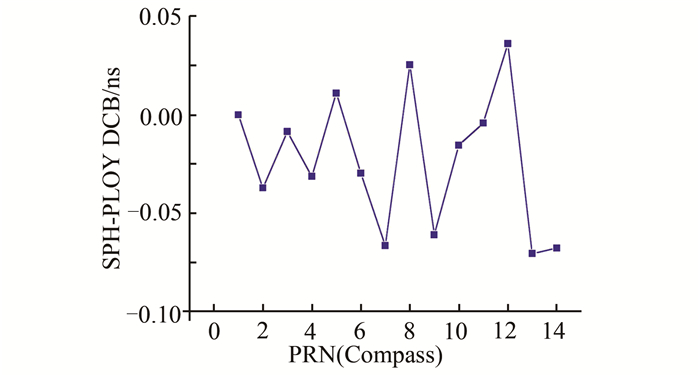
为了验证模型及相关参数等选择的可靠性,本文将低阶球谐函数模型与多项式模型的解算结果进行比较。对中国区域根据文献[4]及实验分析,当球谐函数模型阶数取4,多项式模型取5×6阶,解算精度较好,分别用两种模型对2013年年积日第43天的数据进行解算。图 3是采取上述方法用两种模型解算的北斗卫星的硬件延迟比较结果。从图中可以看出两种模型解算的北斗卫星的DCB差异大多都在0.05 ns以内,表明该区域电离层建模时所用及相关参数的选取是可靠的。
|
| 图 3 两种模型解算的北斗卫星DCB的差值 Fig. 3 The BDS DCB Difference Solved by Two Models |
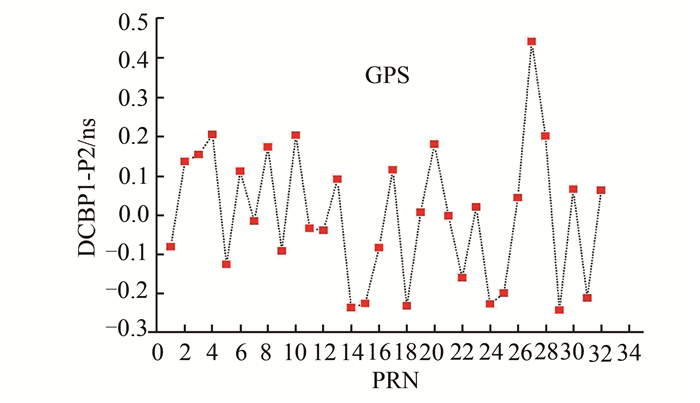
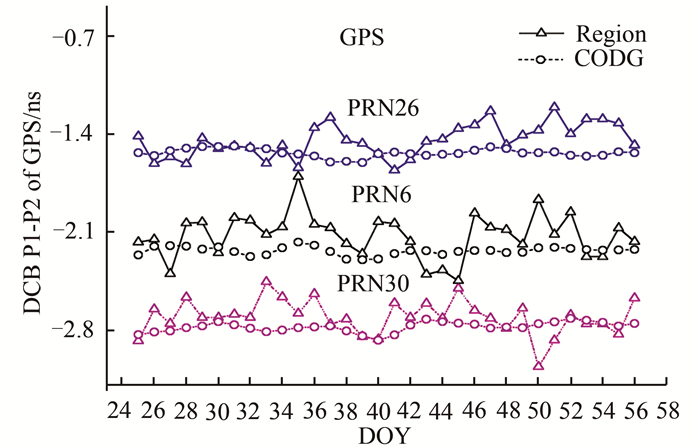
采用前述方法,本文对中国区域及周边的6个BDS/GPS站、7个GPS站共计13个站的数据进行了处理,时段为2013.025(年.年积日)到2013.056,数据采样间隔为30s,截止高度角为20°,北斗观测值类型为B1I、B2I、B1、B2,GPS观测值类型为C1、P2、L1、L2,模型为球谐函数模型,GPS为了便于与欧洲定轨中心(CODE)发布的DCB结果进行比较,需要在计算前用P1-C1的码偏差结果对GPS卫星C/A进行转换,使其与P码保持一致。图 4为2013年1月23日采用联合方式计算的GPS卫星P1-P2硬件延迟与CODE中心的比较结果,图 5是CODE和本文区域模型联合解算的GPS卫星P1-P2硬件延迟随时间的变化结果。从图 4、图 5中可以看出,结果吻合较好,大多数都在0.2 ns左右,个别卫星偏差稍大,主要原因是在区域建模过程中部分卫星的观测数据较少。
|
| 图 4 GPS卫星DCB与CODE的比较结果 Fig. 4 GPS DCB Difference Compared with CODE |
|
| 图 5 GPS卫星的DCB随时间的变化 Fig. 5 The Variation of GPS Daily Solved DCB |
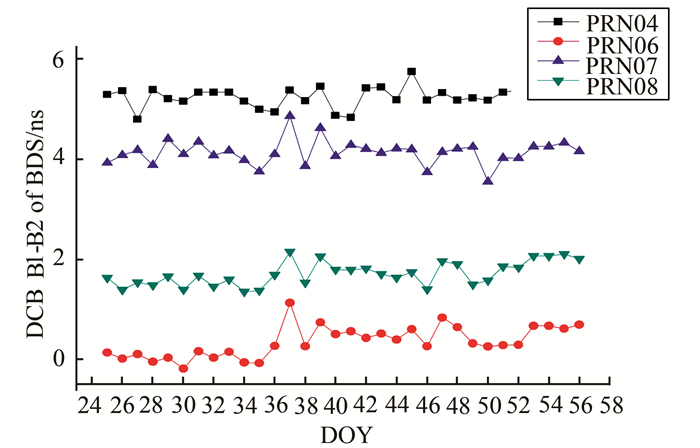
图 6是北斗卫星DCB随时间的变化图,图 7、图 8分别是GPS和北斗卫星DCB标准差(standard difference ,STD)的统计结果。
|
| 图 6 北斗卫星DCB随时间的变化 Fig. 6 The Variation of BDS Daily Solved DCB |
|
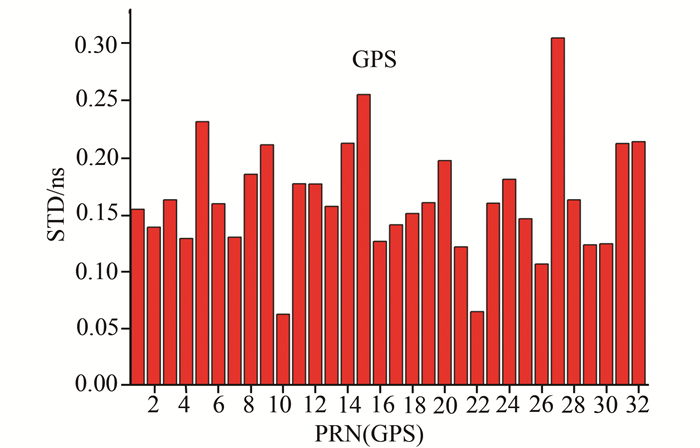
| 图 7 GPS卫星DCB稳定性指标STD的统计结果 Fig. 7 Standard Difference (STD) of GPS Daily Solved DCB |
|
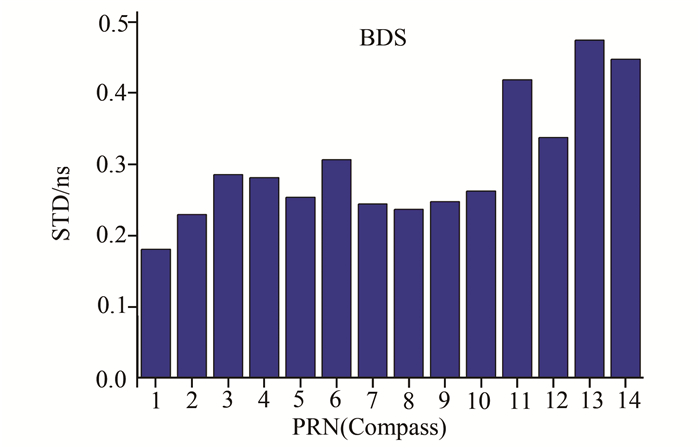
| 图 8 北斗卫星DCB稳定性指标STD的统计结果 Fig. 8 Standard Difference (STD) of BDS Daily Soved DCB |
从图 5、图 7中可以看出GPS卫星的DCB的STD大多都在0.2 ns以内,不如CODE的DCB结果,其主要原因是区域测站少且分布不均,CODE采用全球200多个站,测站观测数据量大。北斗卫星的MEO(11-14)卫星的STD略大于GEO(1-5)、IGSO卫星(6-10),稳定性稍差,可能原因是GEO、IGSO卫星主要分布在中国上空区域,观测数据量远多于MEO卫星。
表 1给出了在这段观测时间内的北斗卫星DCB的平均值及其精度,限于篇幅GPS卫星的DCB结果未给出。从图 8结合表 1可以看出北斗各颗卫星DCB之间差异较大,相对值最大差异为20多ns(相当于6 m),若不考虑硬件延迟对电离层估算的影响,则电离层的估算的精度会大大降低。从总体来看北斗卫星的STD基本都在0.3 ns以内,最大不超过0.5 ns,基本是稳定的。本文中测站数相对较少,如果增加北斗观测站的数量,可以进一步提高北斗卫星DCB解算精度。
| 卫星号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| DCB/ns | 16.24 | 6.22 | 6.22 | 5.31 | -0.78 | 0.35 | 4.14 |
| 精度/ns | 0.18 | 0.23 | 0.29 | 0.28 | 0.25 | 0.31 | 0.24 |
| 卫星号 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| DCB/ns | 1.72 | -6.25 | -7.04 | -7.71 | -7.05 | -6.87 | -4.51 |
| 精度/ns | 0.24 | 0.25 | 0.26 | 0.42 | 0.33 | 0..47 | 0.45 |
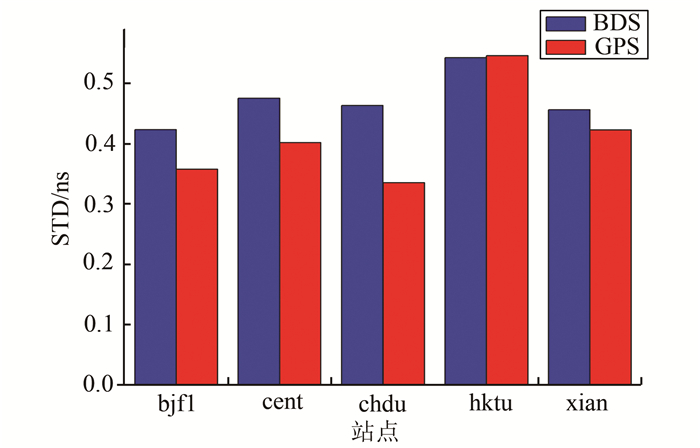
本文中有6个站具有北斗卫星数据,图 9给出了13年1月25日~2月25日的其中5个接收机DCB的STD统计结果,从图中可以看出其稳定性与卫星DCB相比相对较差,但接收机的北斗硬件延迟稳定性与GPS基本相当,都在0.4 ns左右,与CODE所公布的接受机的GPS硬件延迟的STD相差不大,进一步说明该种方法解算的北斗系统硬件延迟的可行性。
|
| 图 9 接收机DCB稳定性指标STD的统计结果 Fig. 9 Standard Difference of Receiver DCB |
本文提出通过联合BDS和GPS测站数据用低阶球谐函数模型解算北斗卫星和接收机的硬件延迟,此种方法有利于克服现有的北斗卫星分布及基准站少等问题,提高北斗卫星的硬件延迟解算精度。结果表明用该方法解算的北斗卫星硬件延迟的精度指标基本都在0.3 ns左右,接收机硬件延迟的STD在优于0.5 ns,稳定性较好,可以满足高精度的电离层模型的要求。随着北斗星座的不断完善,如果采用更多的北斗跟踪站数据,并结合北斗卫星自身的特点会得到更好地效果。
| [1] | Chang Qing. Correct way of GPS Hardware Delay[J]. Chinese Science Bulletin, 2000, 45(15):1676-1680(常青. GPS系统硬件延迟修正方法[J]. 科学通报, 2000, 45(15):1676-1680) |
| [2] | Zhang Hongpin. Modeling Global Ionospheric Delay with IGS Ground Based GNSS Observations[J]. Geomatics and Information Science of Wuhan University, 2012, 37(10):1186-1189(章红平. 地基GNSS全球电离层延迟建模[J]. 武汉大学学报•信息科学版, 2012, 37(10):1186-1189) |
| [3] | Wu Xiaoli, Ping Jinsong, Liu Li, et al. Hardware Delay Solution of Regional Satellite Navigation System[J]. Geomatics and Information Science of Wuhan University, 2011,36(10):1218-1221(吴晓莉, 平劲松, 刘利, 等. 区域卫星导航系统硬件延迟解算[J]. 武汉大学学报•信息科学版, 2011, 36(10):1218-1221) |
| [4] | Zhang Hongpin. Research on Theories and Methods of Monitoring Ionopheric Delay Over China Based on Ground GPS[D]. Shanghai:Graduate University of Chinese Academy of Science,2006(章红平. 基于地基GPS的中国区域电离层监测与延迟改正研究[D]. 上海:中国科学院上海天文台, 2006) |
| [5] | Jin R, Jin S, Feng G. M_DCB:Matlab Code for Estimating GNSS Satellite and Receiver Differential Code Biases[J]. GPS Solutions, 2012, 16(4):541-548 |
| [6] | Jiao W H, Geng C J, Ma Y H, et al. A Method to Estimate DCB of COMPASS Satellites Based on Global Ionosphere Map[C]. China Satellite Navigation Conference(CSNC), Guangzhou, China, 2012 |
| [7] | Schaer S. Mapping and Predicting the Earth' s Ionosphere Using the Global Positioning System[D]. Bern, Germany:The University of Bern, 1999 |
| [8] | Sardón E, Zarraoa N. Estimation of Total Electron Content Using GPS Data:How Stable are the Differential Satellite and Receiver Instrumental Biases[J]. Radio Science, 1997, 32(5):1899-1910 |
| [9] | Li Z, Yuan Y, Fan L, et al. Determination of the Differential Code Bias for Current BDS Satellites[J]. IEEE Transactions on Geoscience & Remote sensing, 2014, 52(7):3968-3979 |
| [10] | Montenbruck O, Hauschild A, Steigenberger P. Differential Code Bias Estimation using Multi-GNSS Observations and Global Ionosphere Maps[J]. Navigation, 2014, 6(13):191-201 |
| [11] | Li Z, Yuan Y, Li H, et al. Two-Step Method for the Determination of the Differential Code Biases of COMPASS Satellites[J]. Journal of Geodesy, 2012, 86(11):1059-1076 |
| [12] | Cui Xizhang. General Surveying Adjustment[M]. Wuhan:Wuhan University Press, 2002(崔希章. 广义测量平差[M]. 武汉:武汉大学出版社,2002) |
| [13] | Geng Changjiang,Zhang Hongping,Zhai Chuanrun. Real time Estimation of DCB Using Kalman Filters[J]. Geomatics and Information of Wuhan University, 2009, 34(11):1309-1311(耿长江,章红平,翟传润. 应用Kalman滤波实时求解硬件延迟[J]. 武汉大学学报•信息科学版, 2009, 34(11):1309-1311) |
| [14] | Zhou Zebo. Analysis of GPS Dual frequency Singer Differenced Receiver Hardware Delay[J]. Geomatics and Information of Wuhan University, 2009, 34(6):724-727(周泽波. 双频GPS接收机单差硬件延迟分析[J]. 武汉大学学报•信息科学版, 2009, 34(6):724-727) |
 2016, Vol. 41
2016, Vol. 41


