文章信息
- 曹建峰, 张宇, 胡松杰, 黄勇, 陈明
- CAO Jianfeng, ZHANG Yu, HU Songjie, HUANG Yong, CHEN Ming
- 嫦娥三号着陆器精确定位与精度分析
- An Analysis of Precise Positioning and Accuracy of the CE-3 Lunarlander Soft Landing
- 武汉大学学报·信息科学版, 2016, 41(2): 274-278
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 274-278
- http://dx.doi.org/10.13203/j.whugis20140123
-
文章历史
- 收稿日期: 2014-07-06

2. 北京航天飞行控制中心, 北京, 100094;
3. 中国科学院上海天文台, 上海, 200030
2. Beijing Aerospace Control Center, Beijing 100094, China;
3. Shanghai Astronomical Observatory, Shanghai 200030, China
嫦娥三号(CE-3)探测器于北京时间2013年12月2日凌晨1点30分发射升空,历经近5天的地月转移轨道、4天100 km高度环月近圆轨道、4天100 km×15 km椭圆轨道后,在12月14日晚降落于月球虹湾区域。在软着陆后,着陆器放置巡视器,开展就位探测,而巡视器开展巡视勘察。着陆器既可通过自身携带的科学仪器开展探测,也可作为通信中继转发巡视器的探测数据。
着陆器的精确定位可以为巡视器的相对定位提供基准,也是对测控系统的基本要求。文献[1]通过惯性组合导航研究确定动力下降段的运动轨迹,文献[2]基于测控网现状对月球着陆器的定位能力进行了仿真分析,并提出了短弧条件下利用数字高程模型设置先验约束的精确定位方法。
本文使用统一X频段(unified X-band,UXB)与甚长基线干涉测量(very long baseline interferometry,VLBI ) 测量数据对着陆器进行统计定位计算,并对定位精度进行分析。
1 着陆器统计定位方法 1.1 测量模型的精确建立由于月球处于地球的引力范围中,理论上测量模型的时间尺度可以采用地球时或质心力学时[3, 4]。但是,月球位置通常通过美国推进喷气实验室提供的行星历表(development ephemeris,DE)获取,因此月球探测器观测模型的建立更适宜在质心参考系中完成,相应的时间系统采用质心力学时。
本节以三程距离测量为例描述观测模型的建立。不同于双程测量,三程测量模式中上行站与下行站不相同,在形式上三程测距的计算可以表示为式(1)[5],双程测量建模只需设置相同的上、下行测站即可。

式中,下标1、2、3分别对应信号上行、转发与下行时刻;TT表示地球时;c表示光速;下标STA1、STA2分别表示上行与下行站;SAT表示卫星;r表示相应的质心天球参考系位置矢量;DRLT表示引力延迟。式(1)中右端第1、2项表示直线距离,第3、4项表示相对论效应引力延迟,对于月球探测该影响可达数米,第5项表示时间系统的差异,与测站位置相关,时间差异引起的三程测距变化可达数十米,但双程测量该项影响则可以忽略。此外,精确的观测建模中还必须考虑潮汐对站址的影响(10 cm量级),广义相对论框架下地球参考系与质心参考系的差异(10 cm量级),地球与太阳作用于月球的潮汐影响(10 cm量级)。
1.2 统计定位原理着陆器的定位计算采用统计定位方法实现。由于着陆器附着于月面,如果不考虑潮汐影响,其在月球固联坐标系下的坐标是固定值,运动方程的建立只涉及到月球固联坐标系与质心天球参考系的转换关系。
月球固联坐标系包括主轴坐标系与平地球平自转轴坐标系(简称为平轴坐标系)。平轴坐标系基于国际天文联合会(IAU)提供的定向参数模型,该坐标系只考虑了月球平极的运动而未考虑章动。主轴坐标系通过3个欧拉角与天球参考系建立联系,DE历表提供了用于转换计算的欧拉角[6]。由于平轴坐标系忽略了月球的章动,其误差可达150 m[7]。因此,定位计算中采用了主轴坐标系描述着陆器的位置。
着陆器跟踪数据的测量方程可以描述为,

式中,Y i表示第i组测量数据;G X ,t i 为非线性函数; V i表示测量噪声。对其在参考状态 X *处进行线性化展开得:

式中,x = X - X *,y i= Y i-G X *,t i ,H i=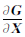 |X-X* =Φ(t i,t 0) 。
|X-X* =Φ(t i,t 0) 。
Φ(t i,t 0) 即为统计定轨中的状态转移矩阵,由行星历表中的欧拉角直接计算。总的观测方程可以表示为:

其线性无偏最小方差估计为式(5),式中 R -1表示观测数据的权重设置。
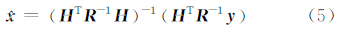
对应的协方差阵为,
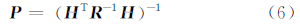
利用式(5)可以对参考状态进行改进,实现统计定位。
2 着陆器定位计算 2.1 测量数据实施软着陆后的近一个月,着陆器独立跟踪时间有限,仅在14日与17日进行了2次跟踪。第一次紧随软着陆,UXB与VLBI设备均参与了跟踪,跟踪弧长约1小时,UXB测量类型包括双程/三程测距与测速,VLBI测量类型包括时延与时延率;而第二次仅UXB设备参与跟踪,跟踪弧长2小时,测量类型为双程测距与测速。
得益于深空站大口径天线的建成与投入使用,以及测量频段的提升,嫦娥三号测量数据的精度较探月一期有了大幅提升。在嫦娥一号任务中,USB测量数据的统计噪声约为1.5 m[8],而深空站UXB双程/三程测距数据的统计噪声优于1 m[9]。VLBI测量数据在嫦娥一号任务中就已经得到了使用,相对于一号任务,VLBI系统在设备上的重大变化是采用数字基带转换器技术取代模拟基带转换器,显著改善了带通非线性效应。同时,VLBI相关后处理部分也进行了一些改进,利用GPS数据对VLBI测站钟速进行校正,改善了CE-1任务中实时模式下时延数据系统差随时间变化的问题,测量精度得到很大改善,其噪声水平至少降低了1~2倍,在嫦娥一号中时延噪声约为1 m(1σ),嫦娥三号中其噪声为0.15~0.45 m(1σ)。 由于采用射电源进行标校,VLBI测量数据系统偏差得到了很好的抑制[10, 11]。嫦娥三号任务中还采用了三程测量,该模式下站间时间同步误差可直接引入测距数据的几十至数百米的系统性偏差,该偏差可在定 轨/定位计算中进行解算。
2.2 定位计算着陆器的定位计算使用了全部可用的UXB及VLBI数据。定位计算中基本参数设置见表 1。JPL发布的DE 421历表中月球轨道与月球光学天平动的构建完全依赖于激光测月数据,使用了包括Apollo 11、14、15与Lunokhod 2激光反射阵的激光测距,共计16 601组数据。通过对近30年测量数据的分析,历表月球轨道精度处于亚米级, 其中在地球视向方向误差仅为几个厘米[6],因而定位计算中不考虑历表误差。
| 项目 | 模型与设置 |
| 行星历表 | JPL DE421 |
| 坐标系 | 月球主轴坐标系 |
| 数据使用设置 | 双程测距:1 m |
| 双程测速:0.3 mm/s | |
| 三程测距:1 m | |
| 三程测速:0.5 mm/s | |
| 时延:0.2 m | |
| 时延率:0.2 mm/s | |
| 解算参数 | 着陆器月固系位置 |
| 佳木斯双程测距系统差 | |
| 三程测距系统差 |
表 2为着陆器定位残差统计信息,时延与测距单位为m,时延率与测速单位为m/s。其中与昆明站相关的时延率误差稍大,较其余基线相差2~3倍,可能与昆明测站设备相关。UXB测量数据中,由于佳木斯测站天线口径较大,其测速精度较喀什精度提升1倍,与环月阶段的精度情况相一致。
| 数据类型 | 测站 | 数据个数 | RMS | |
| VLBI | 时延 | 北京-昆明 | 576 | 0.248 |
| 北京-乌鲁木齐 | 595 | 0.311 | ||
| 北京-上海 | 669 | 0.387 | ||
| 昆明-乌鲁木齐 | 660 | 0.189 | ||
| 昆明-上海 | 2 680 | 0.243 | ||
| 乌鲁木齐-上海 | 669 | 0.102 | ||
| 佳木斯-喀什 | 600 | 0.158 | ||
| 时延率 | 北京-昆明 | 414 | 0.465 | |
| 北京-乌鲁木齐 | 653 | 0.065 | ||
| 北京-上海 | 665 | 0.084 | ||
| 昆明-乌鲁木齐 | 1 636 | 0.469 | ||
| 昆明-上海 | 415 | 0.465 | ||
| 乌鲁木齐-上海 | 666 | 0.148 | ||
| 佳木斯-喀什 | 598 | 0.112 | ||
| UXB | 测距 | 三亚-喀什 | 2 236 | 0.789 |
| 喀什-喀什 | 3 311 | 0.796 | ||
| 佳木斯-喀什 | 3 262 | 0.574 | ||
| 佳木斯-佳木斯 | 6 171 | 0.684 | ||
| 测速 | 喀什-喀什 | 3 368 | 0.331 | |
| 佳木斯-佳木斯 | 5 967 | 0.150 | ||
表 3给出了着陆器定位计算结果,分别给出了主轴与平轴坐标系下的位置分量及经纬度。着陆器在主轴坐标系与平轴坐标系下的位置分量相差约840 m。
| 主轴系 | 平轴系 | |
| X/m | 1 173 283.1 | 1 173 880.1 |
| Y/m | -416 292.2 | -415 907.6 |
| Z/m | 1 208 101.1 | 1 207 653.5 |
| 高度/m | -2 637.6 | -2 637.6 |
| 经度/(°) | 340.464 8 | 340.490 7 |
| 纬度/(°) | 44.139 4 | 44.118 9 |
由于测量数据弧段少,测距系统偏差的解算及定位结果对数据权重的设置非常敏感。为了避免该问题,实际定位计算中固定了喀什站的双程测距的系统偏差,使用了环月阶段对喀什站测距系统差解算结果。
3 定位精度分析由于对着陆器的跟踪弧段较短,且数据类型有限,在定位计算中使用了全部的测量数据,这些对着陆器定位精度的评估是一个难题。通常的外部数据检验与重叠弧段比较方法均不适用于定位精度的分析。本节利用月球高程模型、图像定位结果与协方差分析理论方法对着陆器的定位精度进行分析。
3.1 高程模型比较LRO是美国国家航空航天局的戈达德航天中心于2009年发射的月球探测器。该探测器一个重要的科学目标是利用搭载的高频激光高度计进行全月表的激光测量。基于LRO的激光测高数据科研人员反演了2 050阶次谐系数高程模型与格网高程模型。在高程模型的反演中使用了高精度的轨道数据,整体精度优于10 m,对于月球正面的月海区域精度更高[12]。LRO高程模型使用了月球平轴坐标系,在着陆点附近0.1°×0.1°(约3 km×3 km)的范围内,月面地形平坦,起伏最大约15 m,高程变化的均方根小于3 m,计算着陆点处高程为-2 633 m。
LRO月面高程模型为着陆器定位结果在高程方向的校验提供了基准。计算着陆点的高程与LRO高程模型的差异约4.5 m。在高程模型精度范围内,计算着陆点的高程值与LRO高程模型比较一致。
3.2 LRO图像定位结果的比较2013年12月25日,LRO探测器飞临CE-3软着陆点上空,距离月表约150 km,通过星载窄角相机成功获取了着陆器与巡视器的航拍影像,且分辨率达1.5 m,LRO团队事后通过地形匹配处理获取了较为精确的着陆器位置。表 4给出了LRO团队基于影像数据的定位值[13],同时给出了基于无线电定位结果与LRO视觉定位结果的比较。基于图像数据获取的着陆器位置受限于基准地形的精度以及地形匹配的精度。基准图在水平方向精度优于30 m,垂直方向为5 m[14],而地形匹配可达亚像素级。两种方式获取的着陆器位置在高程方向的差异约为2.4 m,在经纬度方向上,差异约0.002°,反映至月表距离上约为85 m(表 4)。
| 经度/(°) | 纬度/(°) | 高程/m | |
| 图像定位 | 340.488 4 | 44.121 4 | -2 640.0 |
| 无线电定位 | 340.490 7 | 44.118 9 | -2 637.6 |
| 差异 | -0.002 3 | 0.002 5 | 2.4 |
美国德克萨斯大学Tapley将协方差分析理论应用于精密定轨技术研究,可分析待估参数的先验不确定性对参数解算精度的影响,进而分析动力学与测量模型中未模制参数对解算结果的影响[15]。考察协方差形式上可以表示为:

式中,P 表示计算协方差; H x,H c分别表示待估参数与考察参数的偏导数;π=E[(c - c)(c-c)T] 。当π=0时,P c= P ,即考察参数无误差时,考察协方差与计算协方差一致。
本节通过协方差分析理论分析现有测量所能达到的定位能力,使用了定位计算所用的全部数据。基于任务中数据的质量,协方差分析考虑的测量误差包括:测距随机误差为1 m,系统误差为 10 m;测速随机误差0.2 mm/s;时延随机误差0.1 m,系统误差0.1 m;时延率随机误差为0.1 mm/s;站址误差各方向考虑10 cm。考察参数的设置共分为4种情况:① 只考虑测量数据的随机误差,② 考虑测量数据随机误差与站址误差,③ 考虑测量数据随机误差、站址误差与USB测距系统偏差,④ 考虑测量数据随机误差、站址误差以及测距与时延的系统误差。
表 5给出了基于协方差分析给出的不同条件下的定位误差(1σ)。比较①与②,站址误差对定位结果的影响较为显著,在当前测量条件下,各方向10 cm的误差将使得定位精度降低近2倍。如果能完全标校测距与时延数据的系统误差(条件①与②),基于现有数据可以实现10 m量级的定位精度;站址误差与测量误差对定位精度的影响相当。测距数据的系统误差引入,则会显著降低定位精度,而时延数据由于系统误差较小,对定位结果的影响不是很显著。
| 参数设置 | 经度方向/m | 纬度方向/m | 高程/m |
| ① | 3.6 | 2.8 | 0.9 |
| ② | 9.8 | 6.8 | 1.9 |
| ③ | 11.3 | 9.0 | 7.3 |
| ④ | 11.4 | 9.1 | 7.3 |
本文基于统计定位方法,对CE-3月球着陆器使用UXB与VLBI测量数据进行定位计算。基于最新LRO月球数字高程模型,对计算着陆点的高程值进行了验证,两者之间的差异约4.5 m;与LRO光学图像数据的定位结果进行比较,其高程方向差异约2.5 m,三维位置差异约85 m。针对现有的测量数据,基于协方差分析理论分析了可能的定位精度,UXB测距数据的系统偏差是制约定位精度的主要误差源,10 m的系统误差可能会导致定位误差近百米。如果较好的消除系统性偏差,则基于目前的数据可以实现10 m 左右的定位精度。
| [1] | Song Min, Yuan Yunbin. Autonomous Integrated Navigation for Lunar Soft Landing[J]. Geomatics and Information Science of Wuhan University, 2010, 35(9):1013-1016(宋敏, 袁运斌. 月球软着陆自主组合导航研究[J]. 武汉大学学报·信息科学版, 2010, 35(9):1013-1016) |
| [2] | Huang Y, Hu X, Li P, et al. Precise Positioning of the Chang'E-3 Lunar Lander Using a Kinematic Statistical Method[J]. Chinese Science Bulletin, 2012, 57(35):4545-5484 |
| [3] | Tang Geshi. Science and Technology Problems in Tracking and Orbit Determination for Chang'E Probes[J]. Journal of Spacecraft TT&C Technology, 2013, 32(3):189-195(唐歌实.嫦娥探测器轨道测定中的科学与技术问题[J].飞行器测控学报,2013, 32(3):189-195) |
| [4] | Liu Lin, Wang Xin. An Orbital Dynamics of Lunar Probe[M]. Beijing:National Detence Industry Press 2006:23-26(刘林, 王歆. 月球探测器轨道力学[M]. 北京:国防工业出版社, 2006:23-26) |
| [5] | Moyer T D. Formulation for Observed and Computed Values of Deep Space Network Data Types for Navigation[M]. California:Jet Propulsion Laboratory, 2000 |
| [6] | Folkner W M, Williams J G, Boggs D H. The Planetary and Lunar Ephemeris DE421,IOM 343R-08-003[R]. Jet Propulsion Laboratory, California, 2008 |
| [7] | Archinal B A, A'hearn M F, Bowell E, et al. Report of the IAU Working Group on Cartographic Coordinates and Rotational Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements:2009[J]. Celestial Mechanics Dynamical Astronomy, 2011,109:101-135 |
| [8] | Li P J, Hu X G, Huang Y, et al. Orbit Determination for Chang'E-2 Lunar Probe and Evaluation of Lunar Gravity Models[J]. Science China Physics, Mechanics & Astronomy, 2012, 55(3):514-522 |
| [9] | Cao Jianfeng, Hu Songjie, Huang Yong, et al. Orbit Determination and Analysis for Chang'E-2 Extended mission[J]. Geomatics and Information Science of Wuhan University, 2013, 38(9):1029-1033(曹建峰,胡松杰,黄勇,等.嫦娥二号卫星日地拉格朗日L2点探测轨道定轨分析[J].武汉大学学报·信息科学版,2013, 38(9):1029-1033) |
| [10] | Li Jinling, Liu Li, Qiao Shubo. Positioning Analysis of Observations from X-Band Monitoring and Control System Experiments in the Chang'E-2 Project[J]. Journal of Geomatics Science and Technology, 2011, 28(2):84-87(李金岭,刘鹂,乔书波.嫦娥二号卫星X波段测控体制时延定位分析[J].测绘科学技术学报,2011, 28(2):84-87) |
| [11] | Li P J, Hu X G, Huang Y, et al. Orbit Determination for Chang'E-2 Lunar Probe and Evaluation of Lunar Gravity Models[J]. Science China Physics, Mechanics & Astronomy, 2012, 55(3):514-522 |
| [12] | Kreslavsky M A, Head J W, Neumann G A, et al. Lunar Topographic Roughness Maps from Lunar Orbiter Laser Altimeter (LOLA) Data:Scale Dependence and Correlation with Geologic Features and Units[J]. Icarus, 2013, 226:52-66 |
| [13] | NASA Images of Chang'E-3 Landing Site[EB/OL]. NASA/GSFC/Arizona State University. 2013[2014-01-23]. http://www.nasa.gov/content/nasa-images-of-change-3-landing-site/ |
| [14] | Cook A C, Watters T R, Robinson M S, et al. Lunar Polar Topography Derived from Clementine Stereoimages[J]. Joumal of Geophysical Research, 2000,105:12023-12033 |
| [15] | Tapley B D, Schutz B E, George H B. Statistical Orbit Determination[M]. California:Elsevier Academic Press, 2004 |
 2016, Vol. 41
2016, Vol. 41


