文章信息
- 苗岳旺, 周巍, 田亮, 崔志伟
- MIAO Yuewang, ZHOU Wei, TIAN Liang, CUI Zhiwei
- 基于新息χ2检测的扩展抗差卡尔曼滤波及其应用
- Extended Robust Kalman Filter Based on Innovation Chi-Square Test Algorithm and Its Application
- 武汉大学学报·信息科学版, 2016, 41(2): 269-273
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 269-273
- http://dx.doi.org/10.13203/j.whugis20130666
-
文章历史
- 收稿日期: 2014-03-06

2. 61206部队, 北京, 100042
2. Unit 61206, Beijing 100042, China
在组合导航数据处理中,常用到卡尔曼滤波技术。卡尔曼滤波是一种高效的参数估计方法,它通过一定的算法规则对测量新息进行合理的加权,从而实现参数的最优估计。卡尔曼滤波的测量新息服从均值为零的高斯分布[1],如果测量新息中出现异常,那么就会破坏卡尔曼滤波最优估计的特性。在INS/GNSS松组合导航中,由于GNSS信号容易受到外界环境的遮挡和干扰,从而导致GNSS接收机的位置、速度解中存在粗差,这些粗差的存在会破坏测量新息零均值白噪声的特性,从而影响卡尔曼滤波的最优估计性能,甚至引起滤波的发散。在低动态的车载组合导航中,模型误差对系统的影响往往较小,考虑到INS不受外界环境的影响,出现故障的概率比较小,因此GNSS的位置、速度观测粗差成为影响松组合导航精度的主要原因。
针对观测故障问题,常用的有抗差方法[2, 3]和新息χ2检测算法[4]。抗差方法是先对GNSS进行抗差解算,再进行卡尔曼滤波,或者直接把抗差等价协方差矩阵引入卡尔曼滤波的观测协方差矩阵中,从而提高导航系统抵抗粗差的能力。但是在INS/GNSS松组合中,观测量通常使用的是GNSS接收机直接输出的位置和速度,此时就无法使用抗差方法来减小观测粗差的影响。而新息χ2检测算法重在对故障的检测,而非修复,这样在检测到故障时,直接舍去粗差的方法会造成观测值的浪费;如果失锁时间较长,也会引起惯导误差的迅速积累。针对这种情况,本文提出了一种基于新息χ2检测的扩展抗差卡尔曼滤波(extended robust Kalman filter based on innovation chi-square test algorithm,ICT-EREKF)[5],即利用新息向量零均值白噪声的特性和新息χ2检测的原则,构造等价协方差矩阵,从而提高了松组合导航的抗差性能,并结合实测数据对算法的有效性进行了验证,取得了较好的抗差效果。
1 INS/GNSS松组合导航数学模型在INS/GNSS松组合导航中,常采用15维的状态参数构建状态方程[6],在导航坐标系中表示为:
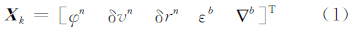
其离散形式的状态方程可以表示为:
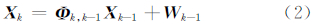
在INS/GNSS松组合中,取INS和GNSS输出的位置、速度之差作为观测值,表示为:
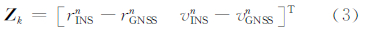
相应的离散形式的量测方程可以表示为:
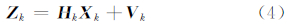
由于惯性导航系统为典型的非线性系统,因此采用EKF算法作为组合导航系统的数据处理方法。离散形式的EKF(extended Kalman filter)算法可以表示为[7, 8]:
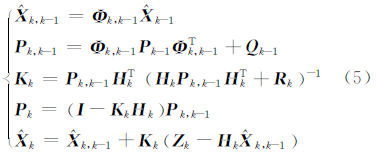
式中,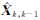 为k-1时刻到k时刻的状态一步预测值; K k为k时刻的增益矩阵; Pk,k-1为k-1时刻到k时刻的状态一步预测协方 差矩阵; Pk为k时刻的状态估计协方差矩阵; Q k为k时刻的系统过程噪声矩阵; R k为k时刻的观测噪声协方差矩阵。
为k-1时刻到k时刻的状态一步预测值; K k为k时刻的增益矩阵; Pk,k-1为k-1时刻到k时刻的状态一步预测协方 差矩阵; Pk为k时刻的状态估计协方差矩阵; Q k为k时刻的系统过程噪声矩阵; R k为k时刻的观测噪声协方差矩阵。
在卡尔曼滤波中,测量新息定义为状态预报值和当前观测值的函数,表示为:
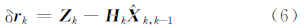
从理论上讲,测量新息为白噪声序列,服从均值为零的正态分布:
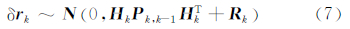
从式(6)来看,测量信息中包含系统模型信息和观测信息,因此可以作为状态估值和观测值是否一致的指标[7]。对于低动态的车载INS/GNSS组合导航系统来讲,系统模型往往要比粗差观测值引起的导航误差小得多。在全闭环的卡尔曼滤波中,通过反馈校正,系统模型误差被控制在一个较小的范围内,因此可以忽略系统模型的影响,于是通过对新息统计量的检测就可以反映观测值是否异常。
当系统无故障发生时,测量新息是均值为零的白噪声序列,当系统发生故障时,测量新息均值便不再为零[9]。将上述故障检测条件转变为假设检验问题:
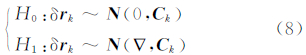
式中,H0为原假设,表示系统无故障发生;H1为备择假设,表示系统发生故障; C k为测量新息的协方差矩阵,其中 C k= H k Pk,k-1 Hk T+ R k。取假设检验统计量为:
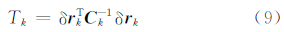
其中,Tk服从自由度为t的χ2分布。根据χ2分布的定义,有:
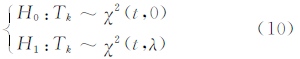
式中,λ为非中心化参数。取显著性水平为α,则系统故障是否发生的边界条件为:

若Tk≤TD,则认为无故障发生,否则应判定系统有故障[10]。根据前面的假设,当Tk > TD时,判定此时有观测异常发生。下面利用χ2分布来构造等价协方差矩阵,以达到抵抗 GNSS观测粗差的目的。
3.2 基于新息χ2检测的扩展抗差卡尔曼滤波通常情况下,当检测到系统故障时,可以放弃当前历元量测值,但这样易造成其他正常测量值的浪费,而且GNSS受干扰的时间较长时,也会引起惯导误差迅速积累。为了充分利用有效的观测历元,本文采用单个新息观测量来构造方差膨胀因子,从而提高卡尔曼滤波的抗差性能。
理想情况下,单个新息观测量也应服从均值为零的正态分布[11],则相应的假设检验统计量为:
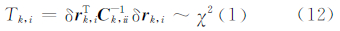
取显著性水平为 α,则单新息值是否有异常发生的边界条件为:

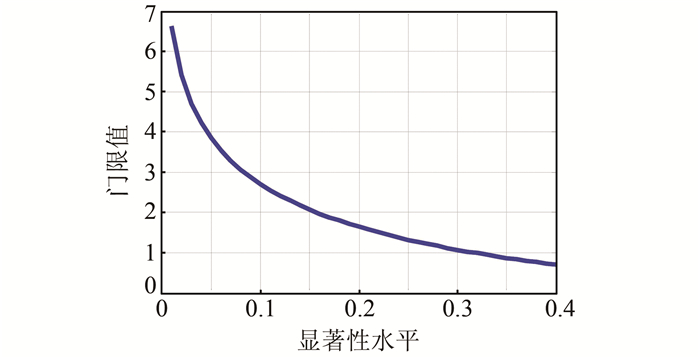
显著性水平α表示原假设成立却拒绝原假设选择备择假设的概率,显著性水平的选择决定了新息统计量的门限值。α值越小,表示所选取的χ2检验的门限值越大。显著性水平与门限值之间的关系如图 1所示。
|
| 图 1 显著性水平α和门限值之间的关系 Fig. 1 Relationship Between Significance Level α and Threshold |
门限值的大小决定了构造方差膨胀因子的临界值的大小,门限值过大或过小都会影响系统的抗差性能。在实际应用中,观测噪声不可能选取得十分准确,由式(12)可知,若观测噪声选取偏小,则会导致统计量值偏大,此 时α的值应该取小些,即粗差的门限值取大些,这样才能避免将噪声当做粗差处理,否则α的值可以适当取大些。α值较为合适的取值范围应为0.01~0.15。
若Tk,i≤T′ D,则认为该观测量无异常,否则应认为该观测量中含有异常值。然后利用等价权函数来构造方差膨胀因子。常用的等价权函数有Huber函数、丹麦函数、IGGI函数等。这里主要采用类似于Huber函数的方法来构造等价权因子:
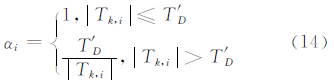
令 α=diag[α1 α2 … αn],0 < αi≤1,i=1,2,…,n,则相应的观测值的等价协方差矩阵为:

将式(5)增益矩阵中的观测协方差矩阵 R k用式(15)中的等价协方差矩阵 Rk代替,即可实现卡尔曼滤波的抗差解。当观测值中有粗差时,通过新息χ2检测算法能够探测到观测粗差,进而再通过对单个新息值的检验来确定粗差观测值的位置,然后依据权因子函数和χ2 检验的临界值来构造等价方差膨胀因子,并通过观测协方差矩阵作用于卡尔曼滤波,降低含有粗差观测值的新息的权重,从而增强卡尔曼滤波的抗差性能,提高组合导航系统的精度。
4 计算与比较为了验证基于新息χ2检测的扩展抗差卡尔曼滤波算法的有效性,本文以一组采集于市区的车载组合导航实测数据为例进行了实验。实验数据由加拿大NovAtel公司生产的SPAN-FSAS分体式组合导航系统采集。该系统的主要指标为陀螺仪零偏小于0.75 °/h,随机游走为0.1 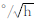 ,加速度计零偏为1 mg,随机游走为0.05 mg/
,加速度计零偏为1 mg,随机游走为0.05 mg/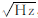 ,采样频率为200 Hz。数据采集时间约为1 h,组合周期为1 s。初始位置误差取10 m,初始速度误差取0.1 m/s,初始姿态误差取0.03°。
,采样频率为200 Hz。数据采集时间约为1 h,组合周期为1 s。初始位置误差取10 m,初始速度误差取0.1 m/s,初始姿态误差取0.03°。
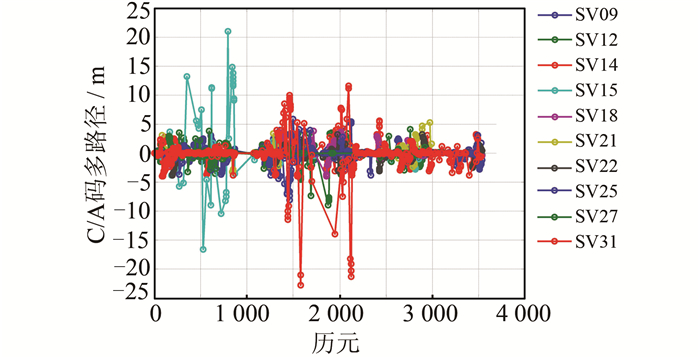
本实验所选择的路线经过了城市市区。在实验过程中,由于GNSS信号受到城市高楼等建筑物的遮挡,失锁比较严重(见图 2),而C/A码的多路径延迟也比较大(见图 3,由teqc软件给出),其中部分时刻卫星的多路径延迟超过20 m,这就必定导致单独的GNSS解中会存在严重的粗差。为了能够对算法进行正确的评价,本文采用高精度的后处理软件Inertial Explorer 8.3的解算结果作为标准轨迹。Inertial Explorer是高精度的GNSS/INS后处理软件,支持基准站加流动站的数据处理模式和双向平滑滤波,其定位精度能够达到cm级。

|
| 图 2 卫星数目变化图 Fig. 2 Variety of Satellite Number |
|
| 图 3 C/A码多路径延迟 Fig. 3 Multipath Delay in C/A Code |
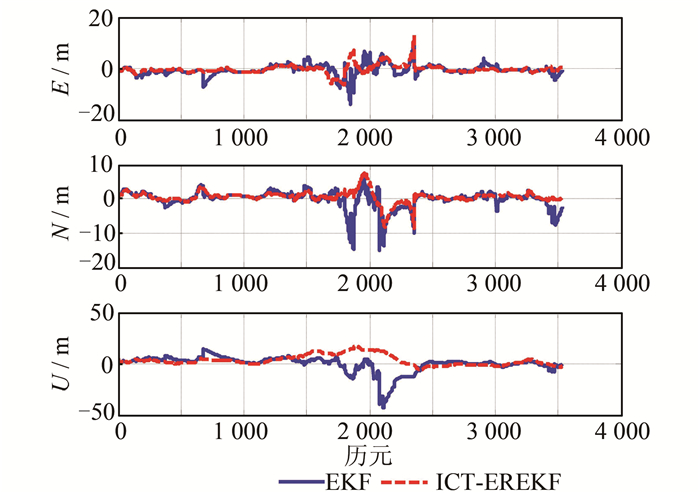
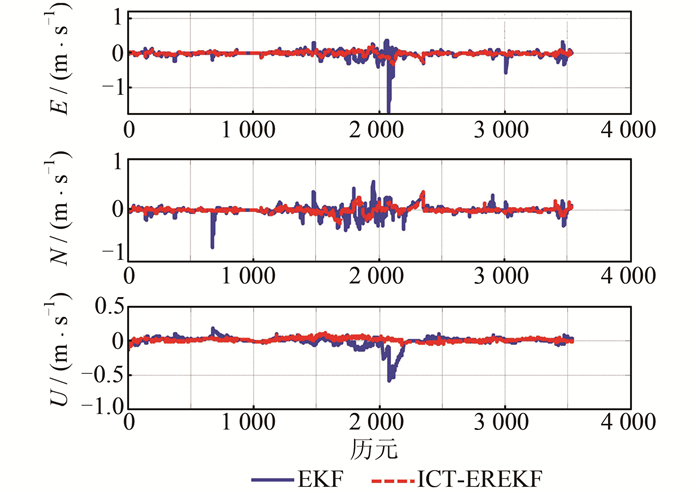
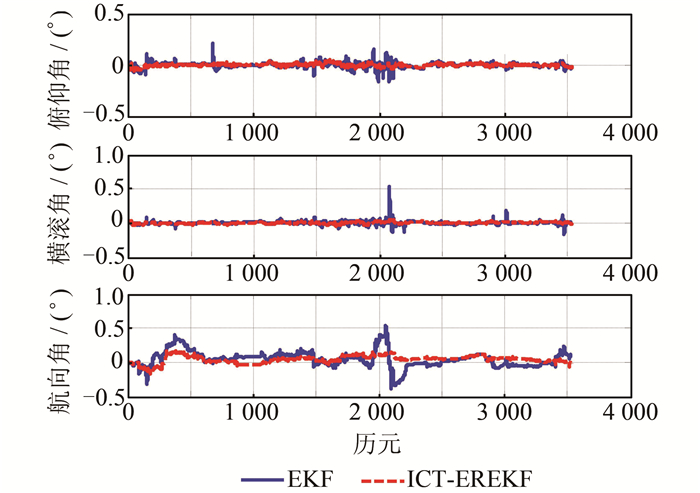
本文采用EKF算法和ICT-EREKF算法两种方案对INS/GNSS组合导航数据进行处理。这里选取E、N、U方向的观测噪声的位置分别为3 m、3 m、5 m,速度分别为0.03 m/s、0.03 m/s、0.05 m/s。为了避免因观测噪声比实际噪声选取得偏小而导致统计量偏大,取显著性水平α=0.05。其中GNSS接收机的位置、速度采用最小二乘算法得出,并舍掉了中误差特别大的结果,组合后的位置、速度、姿态误差如图 4、图 5、图 6所示,RMS统计结果如表 1所示。
|
| 图 4 基于EKF和ICT-EREKF的松组合导航位置误差 Fig. 4 Position Error of Loosely Coupled Integration Based on EKF and ICT-EREKF Algorithms |
|
| 图 5 基于EKF和ICT-EREKF的松组合导航速度误差 Fig. 5 Velocity Error of Loosely Coupled Integration Based on EKF and ICT-EREKF Algorithms |
|
| 图 6 基于EKF和ICT-EREKF的松组合导航姿态误差 Fig. 6 Attitude Error of Loosely Coupled Integration Based on EKF and ICT-EREKF Algorithms |
| EKF | ICT-EREKF | 改善幅度/% | |
| 位置/m | 2.245 | 1.744 | 25 |
| 2.576 | 1.760 | ||
| 7.962 | 6.040 | ||
| 速度/(m·s -1) | 0.112 | 0.051 | 50 |
| 0.09 | 0.058 | ||
| 0.079 | 0.030 | ||
| 姿态/(°) | 0.026 | 0.015 | 46 |
| 0.029 | 0.014 | ||
| 0.125 | 0.067 | ||
分析图 4、图 5、图 6以及表 1,可以得出如下结论:
1) 由于车载INS/GNSS实验过程中GNSS信号受到了建筑物的遮挡和干扰,导致观测伪距 中存在较大的多路径误差(见图 3),从而大大降低了GNSS的导航精度,使导航解中存在粗差。
2) 将INS与含有粗差的GNSS位置、速度进行组合,破坏了卡尔曼滤波的稳定性,导致组合 后的导航结果出现了大的跳变,其中位置误差最大 达到50 m(垂向),速度误差的最大值超过了 1 m/s,而粗差观测值也影响了陀螺仪零偏的估值 精度,从而进一步降低了姿态的估值精度,这说明常规EKF算法并不能有效抵抗观测粗差。
3) 采用基于新息χ2检测的扩展抗差卡尔曼滤波对实测数据进行处理后,导航精度有较大幅度的提高,其中位置精度提高了25%,速度精度和姿态精度提高了45%以上,这说明在检测到故障时,通过观测新息来构造方差膨胀因子,降低含有粗差的GNSS观测值的权重,一定程度上能够提高组合导航系统的精度,从而使组合导航系统能够实时应用于城市街巷等恶劣的导航环境中。
5 结 语本文针对INS/GPS松组合导航中GNSS位置、速度观测量存在的粗差问题,研究了新息χ2算法,并针对松组合导航中缺少多余观测量,难以构造抗差卡尔曼滤波的情况,提出了基于新息χ2检测的扩展抗差卡尔曼滤波,并用实测数据进行了验证,取得了较好的抗差效果。这说明基于新息χ2检测的扩展抗差卡尔曼滤波即使在没有多余观测的情况下,也能够有效处理突变型观测粗差,提高组合导航系统的精度和可靠性,这也为INS/GNSS组合导航算法的研究提供了一种新的思路。
| [1] | Zhang Guoliang, Zeng Jing. Principle and Technology of Integrated Navigation[M]. Xi'an:Xi'an Jiaotong University Press, 2008(张国良,曾静. 组合导航原理与技术[M]. 西安:西安交通大学出版社, 2008) |
| [2] | Gao Weiguang. Research on GPS/INS Adaptive Integrated Navigation Algorithms[D]. Zhengzhou:Information Engineering University, 2008(高为广.GPS/INS自适应组合导航算法研究[D].郑州:信息工程大学, 2008) |
| [3] | Yang Yuanxi. Adaptive Navigation and Kinematic Position[M]. Beijing:Surveying and Mapping Press, 2006(杨元喜.自适应动态导航定位[M]. 北京:测绘出版社, 2006) |
| [4] | Bian Hongwei, Li An, Tan Fangjun, et al. Application of Modern Information Fusion Technology in Integrated Navigation[M]. Beijing:National Defense Industry Press,2010(卞鸿巍, 李安, 覃方君, 等. 现代信息融合技术在组合导航中的应用[M]. 北京:国防工业出版社, 2010) |
| [5] | Miao Yuewang. Research on Data Processing Methods of SINS/GPS Integrated Navigation[D]. Zhengzhou:Information Engineering University, 2013(苗岳旺. SINS/GPS组合导航数据处理方法研究[D]. 郑州:信息工程大学, 2013) |
| [6] | Wu Fumei, Nie Jianliang, He Zhengbin. Classified Adaptive Filtering to GPS/INS Integrated Navigation Based on Predicted Residuals and Selecting Weight Filtering[J]. Geomatics and Information Science of Wuhan University, 2012,37(3):261-264(吴富梅,聂建亮,何正斌. 利用预测残差和选权滤波构造的分类因子在GPS/INS组合导航中的应用[J]. 武汉大学学报•信息科学版, 2012,37(3):261-264) |
| [7] | Groves P D. Principles of GNSS, Inertial, and Multisensor Integrated Navigation Systems[M]. London:Artech House, 2008 |
| [8] | Shin E H. Estimation Techniques for Low-Cost Inertial Navigation[D]. Calgary:The University of Calgary, 2003 |
| [9] | Dong Xurong, Zhang Shouxin, Hua Zhongchun. GPS/INS Integrated Navigation and Its Application[M]. Changsha:National Defense University Press, 1998(董绪荣, 张守信, 华仲春. GPS/INS组合导航定位及其应用[M]. 长沙:国防科技大学出版社, 1998) |
| [10] | Ren Da. Failure Detection of Dynamical Systems with the State Chi-Square Test[J]. Journal of Guidance, Control and Dynamics, 1994, 17(2):271-277 |
| [11] | Quan Wei, Liu Baiqi, Gong Xiaolin, et al. INS/CNS/GNSS Integrated Navigation Technology[M]. Beijing:National Defense Industry Press, 2011(全伟, 刘百奇, 宫晓琳, 等. 惯性/天文/卫星组合导航技术[M]. 北京:国防工业出版社, 2011) |
 2016, Vol. 41
2016, Vol. 41


