文章信息
- 杨建雷, 金天, 黄智刚, 秦红磊, 崔吉慧
- YANG Jianlei, JIN Tian, HUANG Zhigang, QIN Honglei, CUI Jihui
- GNSS信号多径误差非包络评估方法
- A Multipath Error Non-envelope Assessment Method for GNSS Signals
- 武汉大学学报·信息科学版, 2016, 41(2): 262-268
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 262-268
- http://dx.doi.org/10.13203/j.whugis20140073
-
文章历史
- 收稿日期: 2014-04-10

在全球卫星导航系统(global navigation satellite system,GNSS)中,多径效应是影响卫星导航接收机测量精度的一个主要误差源,因此在GPS现代化,Galileo导航系统和北斗卫星导航系统(Beidou navigation satellite system,BDS)信号体制设计过程中,信号抗多径性能的评估是信号体制设计和优化的重要方面。
目前常用的多径误差评估方法主要有用于实际场景测定的评估方法和理论评估方法[1]。前者相对于后者采用较为复杂的分析模型,后者适用于理想条件下信号体制多径性能的对比。
在实际的多径场景中,多径信号与接收天线的周围环境、电离层延时、运动状态及方向图等有关,在不同条件下多径误差所表现出来的特点也是不同的,因此常采用考虑影响多径性能综合因素的统计学方法对信号的多径误差进行测定评估[2]。常用的方法有最大似然估计法[3]和贝叶斯最小均方误差估计法[4],这两种方法已经在实际场景的多径性能评估中得到了广泛的运用[2]。为了消除电离层对码和载波相位的影响,进而能准确地评估多径误差,学者们提出了多径误差双频和多频估计法,并用于实际环境的GPS和Galileo信号多径误差的分析[5, 6]。
常用的多径误差理论评估方法有传统包络法[7]、加权包络法和平均包络法[8]。传统包络法给出了多径误差的隐式表达,利用数值方法求解方程的根,得出多径误差。这种方法能够获得可靠的多径误差包络曲线,反映了在给定的接收条件下一路多径信号所能引入的最大误差和最小误差包络,在GPS现代化和Galileo信号体制设计过程中得到了广泛的应用[9, 10]。为了能分析在不同多径环境下的信号体制的多径误差性能以及得到多径误差的绝对值,学者们在传统包络法基础上分别提出了加权包络法和平均包络法[8]。加权包络考虑了多径反射信号的特点,将不同环境的多径反射和相位延时特性参数[11]引入到传统包络法中,平均包络法则将传统包络法对应的多径误差值取平均得到多径误差的绝对值。多径误差包络给出了多径误差的上界,对动态环境中不可预见的多径误差具有很强的参考价值。
在信号体制评估中,信号源端发射的多径信号的参数是已知的,因此有必要将已知的载波和子载波相位引入到多径误差估计模型中,为信号体制的多径误差提供准确的理论值。针对该问题,本文提出了一种多径误差非包 络评估方法,给出了BPSK、AltBOC、MBOC和BOC信号体制在典型跟踪方法下的多径误差估计模型的理论表达式,对BDS全球信号体制多径误差进行了仿真,并与多径误差包络进行了对比,验证了本文方法的有效性。
1 多径误差包络多径信号分为反射信号和散射信号两种,散射信号往往表现为一个附加的噪声通道,它对伪随机(pseudorandom noise,PN)码跟踪性能的影响很小,因此在导航信号的多径误差分析中仅考虑反射信号的影响。对于PSK信号体制,输入信号与本地载波及PN码混频,假设载波多普勒被完全剥离,则滤波后相应的超前、滞后支路的输出分别为[12]:
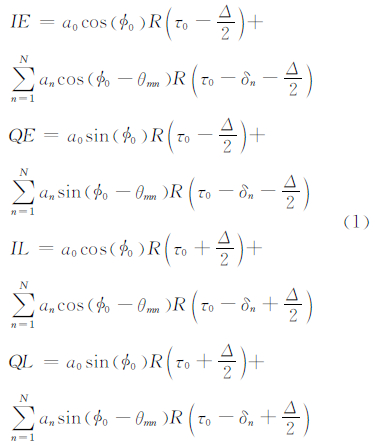
式中,a0和an分别为直达信号和第n路反射信号 幅度;Δ表示早晚码相关器间距;Φ0和τ0表示跟踪环路对直达信号载波相位和码相位时延估计值;δn和θmn分别表示第n路反射信号相对于直达信号的码相位延迟和载波相位误差;N为反射信号的路径数目;R(•)表示码自相关函数,其与功率谱密度的关系为:
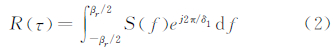
式中,βr为前端带宽; S(f)为信号功率谱密度。
超前减滞后功率(early-minus-late power,EMLP)和点积(dot-product,DP) 鉴相器是跟踪环路鲁棒性最强的两种鉴相器[13]。为了方便导航信号多径误差性能的对比分析且不失一般性,在导航信号评估过程中广泛采用单反射路径的分析模型[14, 15],仅考虑1条反射路径时,EMLP鉴相器输出如下:
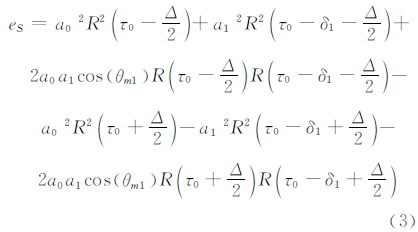
在小误差假设条件下,式(3)可用线形等效模型来表示,即eS≈e 0 +e′ 0 ·τcm,利用码跟踪平衡条件可得码跟踪多径误差τcm:
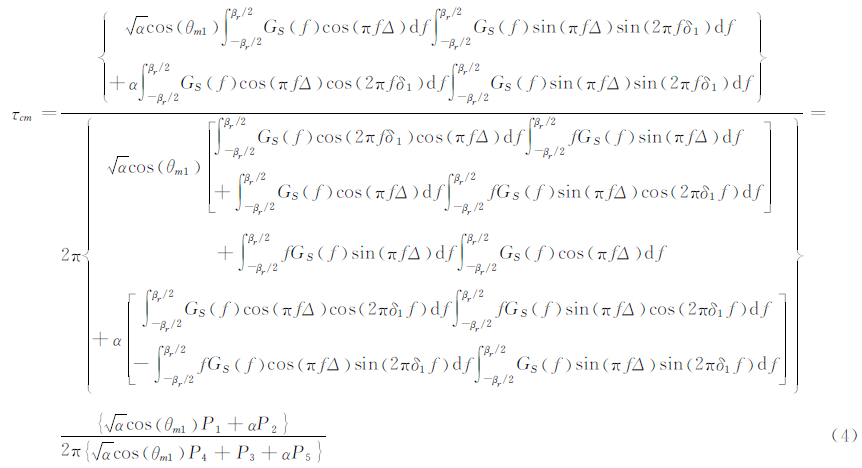
式(4)中,α表示反射信号和直达信号幅度之比(multipath to direct ratio,MDR)。
将θm1=0或π代入式(4)可得PSK信号多径误差传统包络的表达式:
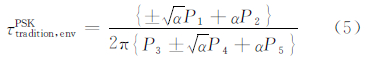
多径误差加权包络反映了与具体环境相关的多径误差估计值,平均包络给出了多径误差的绝对值,由文献[8]可得,加权包络和平均包络表达式分别如式(6)和式(7)所示:

式(6)中,τtypical表示与环境(如开阔地区、乡村、郊区和城市市区等)有关的典型时间延迟[16];式(7)中|• |表示取绝对值。
动态导航系统中,多径环境是复杂多变的,难以对多径效应进行既适合一般应用又适合精确的定量分析。在信号体制评估系统中,反射信号的参数可控,接收端可根据反射信号的参数对信号体制的多径误差性能进行准确的评估,因此采用相对于多径误差包络更为准确的多径误差评估方法是可取的。
2 多径误差非包络评估方法 2.1 PSK信号跟踪环路多径误差非包络评估方法在GPS现代、Galileo和BDS[17]信号体制设计过程中都将采用PSK、AltBOC、 MBOC和BOC信号体制,其中AltBOC、 MBOC和BOC由于其自相关函数的多峰特性,可以采用边带跟踪方法[18, 19]和跳峰法[20],以及适用于MBOC的匹配跟踪法和类BOC(1,1)跟踪法[21, 22]。边带跟踪方法将上述信号的一个边带当作PSK信号,跳峰法、匹配跟踪和类BOC(1,1)跟踪方法将信号剥离载波后直接与本地PN码相关,跳峰法还需要对相关峰进行判断是否是主峰,因此边带处理法、跳峰法、匹配跟踪法和类BOC(1,1)跟踪方法跟踪环路与PSK信号跟踪环路相同。
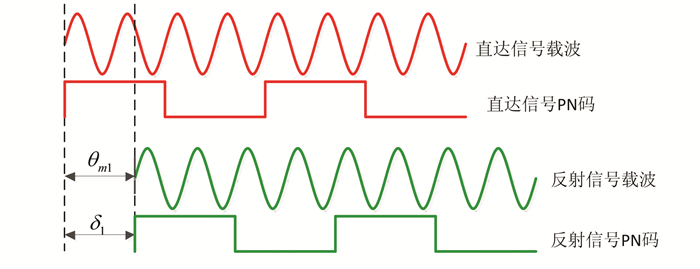
反射信号在延时过程中,不仅PN码有延时,相应的载波相位也有延时,如图 1所示为PSK调制方式的反射信号载波和PN码相对于直达信号的延时示意图。
|
| 图 1 PSK信号体制多径信号载波和PN码 相位延时示意图 Fig. 1 Diagram of Carrier and PN Code Multipath Phase Delay for PSK Signal Structure |
由图 1可以看出,θm1与δ1一一对应,即有式(8)成立:
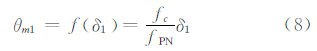
式中,fPN表示PN码速率。
将式(8)代入式(4)可得到 PSK跟踪环路多径误差本文方法表达式如下:
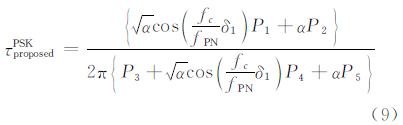
BOC信号除可以采用边带跟踪方法和跳峰法外,还可以采用基于副载波的跟踪方法[23],该方法的环路结构与PSK跟踪环路结构不同。输入信号与本地载波及PN码混频后,假设载波多普勒被完全剥离,则滤波后,相应的超前、滞后支路的输出分别为[23]:
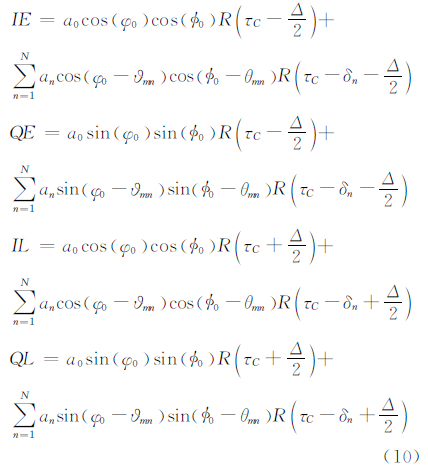
由式(10)可以得到仅考虑1条反射路径时,EMLP多径误差输出如下:
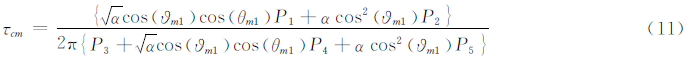
对于反射信号,不仅PN码相位有延时,子载波相位也有延时,有下式成立:
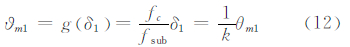
式中,fsub表示子载波频率。
将式(12)代入式(11),对其求极值可得当 θm1=0或π时多径误差达到极值。将θm1=0或π代入式(11)可得 BOC信号采用基于副载波跟踪方法的传统包络如下:
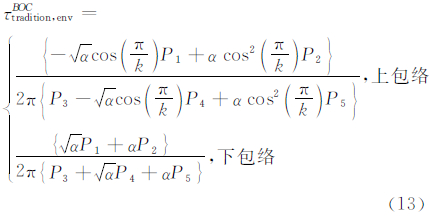
由文献[8]可得,BOC信号跟踪环路多径误差加权包络法和平均包络法如式(14)和式(15)所示:
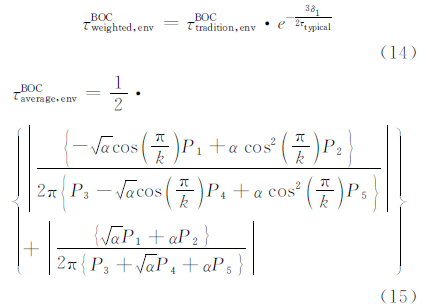
将式(12)代入式(11)可得到BOC跟踪环路的本文方法,表达式为:
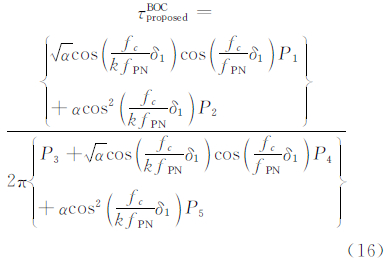
为了证明本文提出的多径误差评估方法的有效性,本文对BDS所采用的BPSK、MBOC、AltBOC和BOC信号体制[17]进行了多径误差性能仿真,并与传统包络、加权包络和平均包络多径误差 曲线对比。信号源端以矢量信号收发仪NI PXIe-5644R为平台,采用LabView语言编程实现,反射信号相位延时和SMR值均在基带通过软件控制;经下变频后,采用数字化仪NI PXIe-5622对数据进行量化采集,存贮介 质采用流盘NI HDD-8265,采样速率150 MS/s,量化比特16 bit,读写速率750 MB/s;采用C语言编写的软件接收机对多径误差进行分析;仿真系统采用铷钟Symmetricom 8040C 10 MHz输出作为同源时钟。
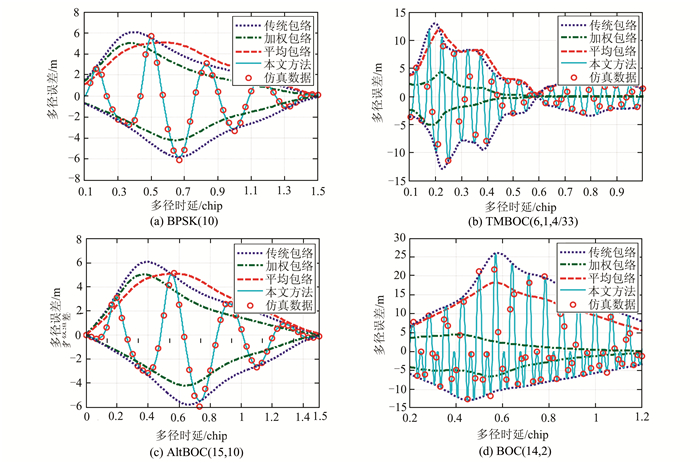
图 2为BPSK(10)、MBOC(6,1)、AltBOC(15,10)和BOC(14,2)信号在单路反射信号存在时,不同多径时延条件下的码跟踪多径误差曲线,其中MBOC(6,1,1/11)信号采用GPS L1C TMBOC(6,1,4/33)生成方式[15, 24],其他信号参数参考文献[17],统计次数为10 000次,MDR为-10 dB,加权包络法中τtypical取乡村和郊区环境下的典型延时值90 m[16],仿真参数如表 1所示。
|
| 图 2 不同信号体制的四种多径误差评估方法对比 Fig. 2 Comparison of Four Multipath Error Analysis Methods of Different Signal Structure |
由图 2可以看出,本文方法仿真与理论曲线统一,能准确地表示被测信号的码跟踪多径误差;传统多径误差包络反映了多径误差在特定SMR值、多径时延和跟踪环路参数条件下,多径误差的极值,可作为本文方法多径误差的上界,对本文方法多径误差估计值具有很强的参考价值;虽然加权包络法综合了环境因素,平均包络法可以得出多径误差的绝对值,但是这两种方法均是以传统包络为基础,给出了在特定条件下的信号的多径误差极值。
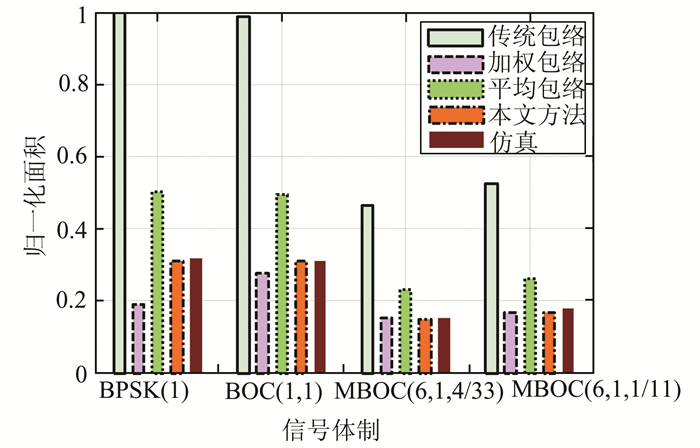
为了进一步验证本文方法在多径误差分析中的有效性,对本方法和包络法与坐标轴围成的面积进行统计,面积的大小可用于比较多径误差的大小[8]。 选取BPSK(1)、 BOC(1,1)、MBOC(6,1,4/33)和MBOC(6,1,1/11)信号,前端带宽为20 MHz,BOC(1,1)、MBOC(6,1,4/33)和MBOC(6,1,1/11)均采用匹配跟踪方法,中频频率与表 1相同。图 3为各种信号体制的多 径误差对比。
|
| 图 3 不同信号体制多径误差对比 Fig. 3 Comparison of Multipath Error of Different Signal Structure |
由图 3可以看出,本文方法得到的理论值与仿真得到的数据最接近。MBOC(6,1,4/33)码跟踪多径误差较小,MBOC(6,1,1/11)次之,BOC(1,1)多径性能优于BPSK(1),这是由于高频分量比重大的信号,其Gabor带宽更大,有利于减小多径误差[14],本文方法与该理论分析相统一。由上述分析可以看出,采用该方法可以正确估计信号体制的码跟踪多径误差,相对于平均多径误差,可提高相对误差57%~61%。
4 结 语本文所提出的多径误差评估方法可以有效地反映反射信号载波和子载波相位延时对码跟踪多径误差的影响,为信号体制评估过程中码跟踪多径误差测试值提供准确的理论参考,且避免了多径误差包络方法中求包络(多径误差极值)的过程。现有的多径误差传统包络法提供了多径误差的极值,可作为本方法多径误差的上界,对本方法多径误差分析值具有很强的参考价值。相对于平均包络误差评估方法提高相对误差57%~61%,能为GNSS信号体制的评估提供有效的理论指导。
| [1] | Irsigler M, Avila-Rodriguez J A, Hein G W. Criteria for GNSS Multipath Performance Assessment[C]. The 18th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2005), Long Beach, CA, 2005 |
| [2] | Krach B, Artaud G. Performance Assessment of Navigation Signals in Realistic Multipath Environments[C]. The 4th ESA Workshop on Satellite Navigation User Equipment Technologies (NAVITEC 2008), Noordwijk, Netherlands, 2008 |
| [3] | Selva J. An Efficient Newton-type Method for the Computation of ML Estimators in a Uniform Linear Array[J]. IEEE Transactions on Signal Processing, 2005,53(6):2036-2045 |
| [4] | Kay S M. Fundamentals of Statistical Signal Processing, Volume 2:Detection Theory[M]. New Jerey, USA:Prentice Hall PTR, 1998 |
| [5] | Simsky A, Sleewaegen J, Nemry P. Early Performance Results for New Galileo and GPS Signals-in-space[C]. European Navigation Conference on Global Navigation Satellite Systems(ENC-GNSS), Manchester, UK, 2006 |
| [6] | Simsky A, Mertens D, Sleewaegen J, et al. Multipath and Tracking Performance of Galileo Ranging Signals Transmitted by GIOVE-B[C].The 21st International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2008), Savannah, Georgia, USA, 2008 |
| [7] | Townsend B R, Fenton P C, Van Dierendonck K J, et al. Performance Evaluation of the Multipath Estimating Delay Lock Loop[J]. NAVIGATION, Journal of the Institute of Navigation, 1995,42:503-514 |
| [8] | Hein G W, Irsigler M, Rodriguez J A, et al. Performance of Galileo L1 Signal Candidates[C]. The European Navigation Conference on Global Navigation Satellite Systems(ENC-GNSS), Rotterdam, The Netherlands, 2004 |
| [9] | Simsky A, Sleewaegen J, Hollreiser M, et al. Performance Assessment of Galileo Ranging Signals Transmitted by GSTB-V2 Satellites[C]. The 19th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2006), Fort Worth, TX, 2006 |
| [10] | Feng Xin, Wang Hua, Tan Shusen. Multipath Performance Analysis for Navigation Signals in Different Pro-correlation Bandwidth and Correlator Spacing[J]. Geomatics and Information Science of Wuhan University, 2011,36(10):1191-1194(封欣, 王华, 谭述森. 预相关带宽和相关器间隔对导航信号多径性能的影响分析[J]. 武汉大学学报•信息科学版, 2011,36(10):1191-1194) |
| [11] | Gaylor D E, Lightsey E G, Key K. Effects of Multipath and Signal Blockage on GPS Navigation in the Vicinity of the International Space Station (ISS)[J]. Journal of The Institute of Navigation, 2005, 52(2):61-70 |
| [12] | Shen Feng,Gai Meng,He Rui.A Novel Method of Multipath Mitigation for PN Code Tracking Loop Based on Wavelet Transform[J]. Journal of Astronautics, 2012,33(11):1667-1673(沈锋, 盖猛, 贺瑞. 一种基于小波变换的伪码跟踪环路多径抑制方法[J]. 宇航学报, 2012,33(11):1667-1673) |
| [13] | Julien O. Design of Galileo L1F Receiver Tracking Loops[D]. Canada:University of Calgary, 2005 |
| [14] | Tang Zuping, Hu Xiulin, Huang Xufang. Analysis of Multipath Rejection Performance in GNSS Signal Design[J]. J. Huazhong Univ. of Sci. & Tech. (Natural Science Edition), 2009,5:1-4(唐祖平, 胡修林, 黄旭方. 卫星导航信号设计中的抗多径性能分析[J]. 华中科技大学学报:自然科学版, 2009,5:1-4) |
| [15] | Tang Zuping. Research on Relevant Theory for GNSS Signal Design and Evaluation[D]. Wuhan:Huazhong University of Science and Technology, 2009(唐祖平. GNSS信号设计与评估若干理论研究[D]. 武汉:华中科技大学, 2009) |
| [16] | Van Nee R. Spread-spectrum Code and Carrier Synchronization Errors Caused by Multipath and Interference[J]. IEEE Transactions on Aerospace and Electronic Systems, 1993,29(4):1359-1365 |
| [17] | Yang Y. China Reveals Updated Compass/Beidou-2 GNSS Signal Plan[OL]. http://www.insidegnss.com/node/1624,2009 |
| [18] | Jovanovic A, Mongrédien C, Tawk Y, et al. Two-Step Galileo E1 CBOC Tracking Algorithm:When Reliability and Robustness Are Keys![J]. International Journal of Navigation and Observation, 2012:1-14 |
| [19] | Kacmarík P, Kovár P, VEJRAZKA F. Galileo Alt-BOC E5 Signal Characteristics for Optimal Tracking Algorithms[C]. The Navigation Conference & Exhibition, London,UK, 2009 |
| [20] | Fine P, Wilson W. Tracking Algorithm for GPS Offset Carrier Signals[C]. The 1999 National Technical Meeting of the Institute of Navigation, San Diego, CA, 1999 |
| [21] | Simona Lohan E. Analytical Performance of CBOC-modulated Galileo E1 Signal Using Sine BOC (1, 1) Receiver for Mass-market Applications[C]. The 2010 IEEE/ION Position Location and Navigation Symposium (PLANS), Indian Wells, CA, USA, 2010 |
| [22] | Yao Zheng, Liu Linlin, Zhang Xiaoming. GNSS Interoperable Signal Modulation for Multiple Receiving Modes[J]. Geomatics and Information Science of Wuhan University, 2012, 37(5):621-625(姚铮, 刘琳琳, 张晓明, 等. 面向多接收模式的GNSS互操作信号调制[J]. 武汉大学学报•信息科学版, 2012, 37(5):621-625) |
| [23] | Yang Zaixiu, Huang Zhigang, Geng Shengqun. Novel Tracking Loop of BOC Signal Based on Subcarrier Tracking[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011,37(2):245-248(杨再秀, 黄智刚, 耿生群. 基于副载波跟踪的BOC信号跟踪环路设计[J]. 北京航空航天大学学报, 2011, 37(2):245-248) |
| [24] | Charles Cahn, Charles Wang, Chris Hegarty, et al. Enhancing the Future of Civil GPS:Overview of the L1C Signal[OL]. http://www.insidegnss.com/node/485,2007 |
| [25] | Misra R, Palod S. Code and Carrier Tracking Loops for GPS c/a Code[J]. International Journal of Pure and Applied Sciences and Technology, 2011,6(1):1-20 |
 2016, Vol. 41
2016, Vol. 41


