文章信息
- 王乐洋, 许光煜
- WANG Leyang, XU Guangyu
- 加权总体最小二乘平差随机模型的验后估计
- Application of Posteriori Estimation of a Stochastic Model on the Weighted Total Least Squares Problem
- 武汉大学学报·信息科学版, 2016, 41(2): 255-261
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 255-261
- http://dx.doi.org/10.13203/j.whugis20140275
-
文章历史
- 收稿日期: 2015-03-01

2. 流域生态与地理环境监测国家测绘地理信息局重点实验室, 江西南昌, 330013;
3. 武汉大学测绘学院, 湖北武汉, 430079
2. Key Laboratory of Watershed Ecology and Geographical Environment Monitoring, NASG, Nanchang 330013, China;
3. School of Geodesy and Geomatics, Wuhan University, Wuhan 430079, China
近年来,加权总体最小二乘平差是测绘数据处理领域研究的热点问题。目前,处理加权总体最小二乘问题的算法有Schaffrin-Wieser算法[1]、Mahboub算法[2]和Amiri-Simkooei算法[3]等。通过对加权总体最小二乘已有算法的进一步分析发现,在平差前随机模型要已知验前方差才能精确地给观测数据定权。在过去很长时间,平差都在单一的同类观测量中进行,例如测角网平差、水准网平差;定权都是采用测量平差中常用方法定权,例如水准高差按路线长度倒数定权等。随着平差对象从单一同类观测扩展为不同类的多种观测量,一般它们的验前方差都不能精确已知,而且实践证明,原先采用的估计验前方差确定各类观测量权的方法,在许多情况下不够准确。为了提高方差估计的精度,20世纪70年代开始出现了用验后信息估计各类观测量方差,然后定权的方法。方差分量估计(VCE)主要有赫尔默特估计(Helmert)[4]、最小范数二次无偏估计(MINQUE)、最优不变二次无偏估计(BIQUE)及VCE的扩展研究[5, 6],这些都是在最小二乘准则的基础上进行的,没有顾及系数矩阵的误差。对于以上存在的问题,文献[7, 8]将总体最小二乘问题和VCE进行了综合研究,分别采用LS-VCE和MINQUE-VCE对总体最小二乘问题中观测向量和系数矩阵元素的方差分量进行求解,从而得到更准确的参数估计值。针对EIV模型中存在随机模型不明确,参数估计不准确的问题,本文提出了一种加权总体最小二乘平差随机模型的验后估计方法,既考虑到观测向量 y和系数矩阵A 中元素可能具有不同精度的情况,又顾及到在给观测向量 y和系数矩阵A 中元素定权时所选取的初始单位权方差可能不同导致定权不准确的问题。在算例部分,第1个算例采用文献[9]中的实验数据,将本文算法与文献[3]、[7]中的算法进行了比较,验证本文算法的可行性;第2个直线拟合和第3个线性参数估计算例,主要对本文的验后估计算法和本文提出的加权总体最小二乘快速算法,以及最小二乘算法进行了比较,实验表明本文提出的算法在解决随机模型不准确的总体最小二乘问题时更合理、有效。
1 加权总体最小二乘平差随机模型 的验后估计 1.1 加权总体最小二乘快速算法当同时考虑系数矩阵和观测向量误差时,有EIV模型为:

式中,y ∈ R n×1为观测向量; e y 为观测向量的随机误差; A ∈ R n×m为列满秩的系数矩阵; E A 为系数矩阵的随机误差; X ∈ R m×1为待估参数向量;其随机模型分别为:

式中,e A =vec( E A ),即 e A 是将 E A 按列向量化后得到的nm×1列向量; P y 和 P A 分别为 e y 和 E A 的列向量化,即vec( E A )的权阵;σ012为观测向量的单位权方差;σ022为系数矩阵元素的单位权方差。
假设 e y 、 E A 的估值分别为 ,则加权总体最小二乘平差准则为:
,则加权总体最小二乘平差准则为:

一般的加权总体最小二乘中观测值和系数阵中的元素是相互独立的,且系数矩阵中的元素通常是由其他观测值经过计算得到的,也就是观测值和系数阵中元素的随机模型是不相同的;在总体最小二乘平差之前给定的观测值的权阵 P y 和系数矩阵元素的权阵 P A 是不恰当的,或者说它们所对应的单位权方差σ012和σ022不相等,因此对这个问题必须利用平差后的结果进行处理,这就是加权总体最小二乘平差随机模型的验后估计。
设参数 X 的估值为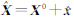 ,
其中 X 0表示参数
,
其中 X 0表示参数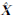 的近似值,
的近似值,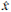 为未知参数近似值的改正数,观测值的估值
为未知参数近似值的改正数,观测值的估值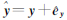 ,总体最小二乘平差除了考虑观测值 y 的误差
,总体最小二乘平差除了考虑观测值 y 的误差 外,同时还考虑系数矩阵 A 的误差
外,同时还考虑系数矩阵 A 的误差 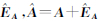 。根据式(1)有:
。根据式(1)有:

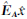 ,得:
,得:

令 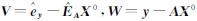 ,则式(5)变为:
,则式(5)变为:

所以,加权总体最小二乘准则式(3)变为:

结合式(6)、式(7)得加权总体最小二乘的估值:
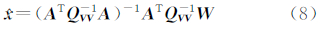
式中,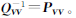 。
。

式中, ,其中 I n表示n阶单位阵,
,其中 I n表示n阶单位阵, 是Kronecker积算子;
是Kronecker积算子;

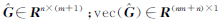 。其中
。其中  表示列向量
表示列向量 的第i个元素,
的第i个元素, 表示矩阵
表示矩阵 的第(i,j)个元素。
的第(i,j)个元素。
若已知列向量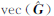 中的所有元素
中的所有元素
 、
、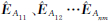 之间的互协因数及协因数组成的矩阵
之间的互协因数及协因数组成的矩阵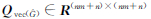 ,则由式(9)根据协因数传播律得:
,则由式(9)根据协因数传播律得:
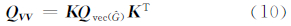
单位权方差的估计为:

参数估值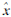 的协因数阵为:
的协因数阵为:

式中,Q y 表示观测向量 y 的协因数阵。
将式(6)和式(8)代入式(9)得:
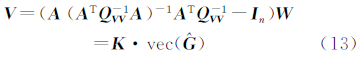
由最小二乘条件平差得:
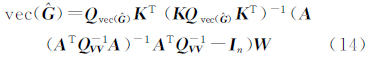
由此可以得到观测值及系数阵随机误差的估值 和
和 ,对应的单位权方差估值分别为:
,对应的单位权方差估值分别为:

式中,r y 为观测向量 y 对应的自由度;r A 为系数矩阵 A 对应的自由度。
加权总体最小二乘快速算法(简称fast-WTLS)迭代过程如下。
1) 给定已知或者观测数据 A 、 y 、 P A 、 P y ;
2) 设置估计值的初值为:
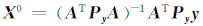
3) 利用式(8)、(10)计算 QVV 、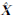 ,从而得到
,从而得到 ;
;
4) 如果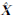 与上轮迭代的差值范数小于设定的阈值,则终止迭代得到最终解;否则更新参数近似值
与上轮迭代的差值范数小于设定的阈值,则终止迭代得到最终解;否则更新参数近似值 ,转到步骤3),重复迭代计算。
,转到步骤3),重复迭代计算。
将式(4)进行调整,结合公式

得:

式中,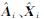 表示fast-WTLS算法迭代过程中第i次迭代计算得到的系数矩阵和未知参数的值;Δ A i、Δ X i为迭代过程中相应的改正数。
舍去二次项Δ A iΔ X i,式(17)、式(18)可以改写为[8]:
表示fast-WTLS算法迭代过程中第i次迭代计算得到的系数矩阵和未知参数的值;Δ A i、Δ X i为迭代过程中相应的改正数。
舍去二次项Δ A iΔ X i,式(17)、式(18)可以改写为[8]:
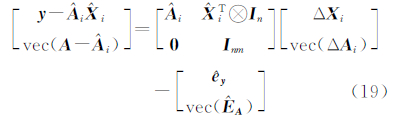
令  ,
, ,
, 。
。
式(19)可以表示为:

且有下列关系式:
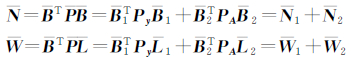
式中,权阵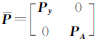 。
。
此时便可以借鉴Welsch推证的赫尔默特方差估计严密公式[4]得到EIV模型的方差分量估计公式(Helmert-VCE)。
在EIV模型中,赫尔默特方差分量估计公式可以表示为:

式中,

 表示迹算子。
表示迹算子。
通过对式(21)求解,可以得到观测向量和系数矩阵的方差分量:

本文提出的方差分量求解方法是将函数模型式(19)表示成间接平差的形式,通过间接平差模型下的Helmert-VCE公式推导得到EIV模型中方差分量估计公式,因此EIV模型的精度评定和多余观测数的求解工作完全可以在此基础上按间接平差的原理继续进行。EIV模型的多余观测数估计公式为:
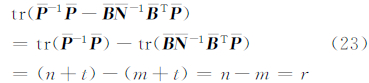
EIV模型的观测数据分为两个部分,分别为n个观测向量元素和t个系数矩阵中观测元素(随机变量),共n+t个。求解的参数也分为两个部分,分别是m个模型参数和t个系数矩阵的待估计量(随机变量),共m+t个。因此,EIV模型和高斯-马尔科夫模型相比,自由度没有变化[8, 12]。
同样可以得到观测向量和系数矩阵的多余观测分量:

加权总体最小二乘平差随机模型验后估计的迭代计算步骤为:
1) 给定观测值和系数矩阵权阵的初值 P y1和 P A1,求得 Q y1和 Q A1,然后组成 ;
;
2) 进行第一次加权总体最小二乘平差,由式(14)求得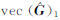 ,从而得到观测值及系数阵第一次平差后的
,从而得到观测值及系数阵第一次平差后的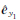 和
和 ;
;
3) 根据式(15)、式(16)、式(24)、式(25)分别得到观测值及系数阵第一次平差后的单位权方差估值 和
和 ;
;
4) 依式(26)重新定权:
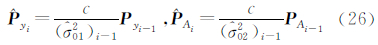
式中,c为任一常数,一般是选 或
或 中的某个值,i≥1为迭代次数。求得( Q y )i和( Q A )i,然后组成
中的某个值,i≥1为迭代次数。求得( Q y )i和( Q A )i,然后组成  ;
;
5) 进行步骤2)~4),即平差—单位权方差估计—定权后再平差,直到
 为止。
为止。
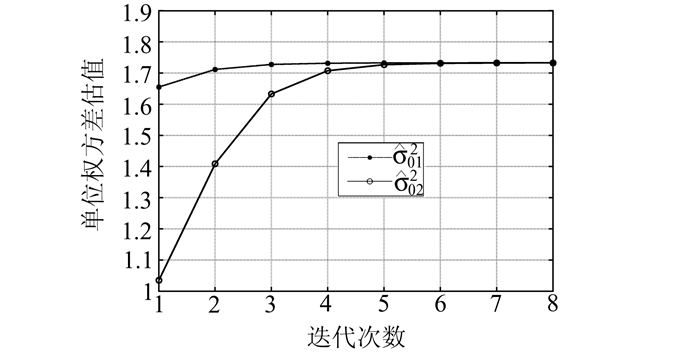
为了检验本文提出的加权总体最小二乘平差随机模型验后估计方法的效果,采用文献[9]中的直线拟合数据,利用本文提出的算法进行参数求解,并与文献[3]中的加权总体最小二乘算法(WTLS),文献[7]中提出的最小二乘方差分量估计(LS-VCE)结合加权总体最小二乘算法,以及文献[3]中的WTLS算法结合本文提出的Helmert-VCE方法所求得的参数结果进行比较,以分析这四种算法的差异。结果见表 1,上述方法所求得的单位权方差估值计算结果见表 2。图 1表示迭代计算过程中两个方差分量的收敛图。
|
图 1 算例2.1中线性回归模型迭代过程中
Fig. 1 Estimates of Two Variance Factors 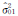 and
and 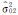 of Linear Regression Model over Different Iteration Steps
of Linear Regression Model over Different Iteration Steps
|
假设直线方程为:

直线拟合的模型为式(27),系数矩阵所对应的协因数阵 Q A 为式(28):
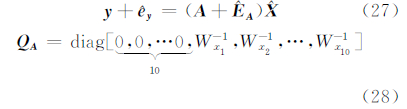
1) 在加权总体最小二乘算法[3]中,把观测向量和系数阵所对应的单位权方差当作相同,得到的参数结果与文献[9]中提供的“参数真值”基本一致。在采用方差分量估计结合WTLS中,考虑了观测向量和系数阵的验前单位权方差一般不能准确已知或二者是不同的,例如在直线拟合模型中,就考虑了x和y具有不同的单位权方差分量 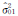 和
和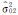 ;因此,参数的估计结果就得到了进一步改正。
;因此,参数的估计结果就得到了进一步改正。
2) 从表 1可以看出,采用方差分量估计结合加权总体最小二乘方法(包括本文方法)求解的参数结果与文献[9]提供的“参数真值”有差别,这是合理的,因为文献[9]中的数据和权值是由不同人给出的,无法确定权值的准确性,采用WTLS算法进行参数求解,显然不合理。文献[7]中也对文献[9]提供的“参数真值”的准确性提出了质疑,认为在确定观测向量和系数阵权阵时采用了不同的单位权方差,因此权阵并不合理。
3) 本文提出的加权总体最小二乘平差随机模型验后估计方法实质是fast-WTLS和赫尔默特方差分量估计的结合。其中fast-WTLS算法是一种近似的WTLS算法[13],从算法结构可以看出,该方法的求解更接近最小二乘算法,在进行数据处理时更快速、便捷。从表 1中可以看出,本文算法和WTLS结合LS-VCE算法求解得到的参数结果有差异,而WTLS结合Helmert-VCE算法与WTLS结合LS-VCE算法求解得到的参数结果基本相同,从而可以判断本文算法与WTLS结合LS-VCE算法的差异存在于求解参数的加权总体最小二乘算法中,而方差分量估计部分Helmert-VCE与LS-VCE等价。
4) 在EIV模型中,LS-VCE首先设定方差分量初值,一般设为1,经过迭代得到不同的方差分量估值,而迭代过程中相应的协因数阵不变;而Helmert-VCE估计是通过方差分量修改权阵,达到最终方差分量一致,其中权阵变了。两种方法最终都能达到统一单位权方差的目的。从表 2中单位权方差估值的计算结果也可以看出这一点。
5) 对于非线性模型,fast-WTLS算法在推导过程中出现了非线性化的情况,通过对二次项的舍弃达到了模型的线性化,因此对于非线性问题也可以较好的处理。
2.2 模拟直线拟合算例利用Matlab软件编程进行数值模拟实验,模拟普通直线 y=β1+β2x,其不含误差的x、y值见表 3。待估的未知参数分别为直线的斜率β2和截距β1,真值为β2=5、β1=8。在观测值x和y上分 别加入均值为0,方差为σx2=σ012· P-1x和σ2 y =σ022· Py -1 的随机误差,其中σ012=1,σ022=0.25;采用本文提出的加权总体最小二乘平差随机模型的验后估计进行求解,并与最小二 乘(LS) 、fast-WTLS所求解的参数结果进行比较。参数估值结果见表 4。图 2表示普通直线拟合算例中两个方差分量的收敛图。
| 点号 | xtrue | ytrue | x | y | Px | Py |
| 1 | 0.0 | 8.0 | -0.074 424 | 7.704 983 | 500.0 | 1.0 |
| 2 | 0.9 | 12.5 | 0.872 194 | 12.657 537 | 100.0 | 1.8 |
| 3 | 1.8 | 17.0 | 1.600 373 | 17.117 909 | 70.0 | 4.0 |
| 4 | 2.6 | 21.0 | 2.455 037 | 21.011 701 | 70.0 | 8.0 |
| 5 | 3.3 | 24.5 | 3.445 871 | 24.536 566 | 20.0 | 20.0 |
| 6 | 4.4 | 30.0 | 4.642 084 | 30.112 483 | 20.0 | 20.0 |
| 7 | 5.2 | 34.0 | 4.969 869 | 34.015 362 | 8.0 | 70.0 |
| 8 | 6.1 | 38.5 | 5.627 811 | 38.421 008 | 4.0 | 70.0 |
| 9 | 6.5 | 40.5 | 7.189 325 | 40.500 002 | 1.8 | 100.0 |
| 10 | 7.4 | 45.0 | 7.345 081 | 45.020 373 | 1.0 | 500.0 |
| 真值 | LS | fast-WTLS |
fast-WTLS结合 Helmert-VCE | |
 | 5 | 4.826 204 402 | 4.841 768 064 | 4.907 255 311 |
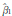 | 8 | 8.734 877 616 | 8.725 097 232 | 8.546 508 439 |
 | — | 0.755 149 005 | 0.742 161 264 | 0.554 322 155 |

|
图 2 算例2.2中线性回归模型迭代计算
过程中两个方差分量估计值
Fig. 2 Estimates of Two Variance Factors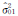 and and 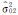 of Linear Regression Model over Different
Iteration Steps of Linear Regression Model over Different
Iteration Steps
|
模拟一个线性参数估计 问题,有 Ax = b ,其不含误差的设计矩阵 A ∈ R n×m和观测值 b ∈ R n×1见表 5。待估的未知参数有5个,x =[x1 x2 x3 x4 x5]T ,真值 =[1 1 1 1 1]T。观测值 b的噪声e ~N( 0 ,σ012Pb -1 ),其中σ012=0.1,P b =diag(1,2,…,n)。设计矩阵元素的误差为 e A ~N(0,σ022 PA -1 ),其中σ022=0.5,P A =diag(n×m,n×m-1,…,2,1);采用本文算法求解参数,并与 LS、fast-WTLS所求解的参数进行比较,参数估值结果见表 6。图 3表示线性参数估计算例中两个方差分量的收敛图。
=[1 1 1 1 1]T。观测值 b的噪声e ~N( 0 ,σ012Pb -1 ),其中σ012=0.1,P b =diag(1,2,…,n)。设计矩阵元素的误差为 e A ~N(0,σ022 PA -1 ),其中σ022=0.5,P A =diag(n×m,n×m-1,…,2,1);采用本文算法求解参数,并与 LS、fast-WTLS所求解的参数进行比较,参数估值结果见表 6。图 3表示线性参数估计算例中两个方差分量的收敛图。
| Atrue | Btrue | A | b | ||||||||
| 2.00 | -5.00 | 3.00 | 4.00 | -9.50 | -5.50 | 2.040 226 | -4.918 413 | 1.213 904 | 3.988 521 | -9.259 413 | -5.525 789 |
| -2.00 | 4.00 | 1.80 | -1.05 | 8.50 | 11.25 | -2.054 385 | 3.893 551 | 1.846 389 | -0.926 856 | 8.194 207 | 11.531 353 |
| 2.00 | -1.00 | -3.40 | 5.05 | 2.45 | 5.10 | 1.988 241 | -1.029 742 | -3.560 407 | 5.036 389 | 2.419 557 | 5.368 116 |
| 3.75 | 4.50 | 7.00 | -3.50 | -9.00 | 2.75 | 3.937 925 | 4.358 928 | 7.022 607 | -3.527 178 | -8.802 020 | 2.755 208 |
| 1.00 | -2.20 | 3.35 | -7.50 | 6.40 | 1.05 | 0.789 243 | -2.008 545 | 3.457 634 | -7.498 851 | 6.157 306 | 1.289 353 |
| 2.40 | 5.65 | -2.50 | 8.40 | 2.49 | 16.44 | 2.332 857 | 5.694 643 | -2.695 364 | 8.205 630 | 2.379 488 | 16.501 416 |
| 3.50 | -2.80 | 3.00 | 9.50 | 12.70 | 25.90 | 3.479 874 | -2.830 425 | 3.162 853 | 9.189 329 | 12.710 476 | 25.944 048 |
| 5.70 | -3.00 | -2.40 | 5.50 | -2.80 | 3.00 | 5.715 989 | -3.113 916 | -2.036 491 | 5.810 167 | -2.002 947 | 3.245 073 |
| 7.20 | 4.50 | 2.90 | -2.51 | 7.50 | 19.59 | 7.005 363 | 4.512 333 | 2.665 135 | -2.450 270 | 7.729 512 | 19.751 875 |
| 4.00 | 1.00 | -2.00 | 2.00 | 5.00 | 10.00 | 4.058 426 | 1.213 904 | -2.318 891 | 1.746 801 | 4.717 644 | 10.090 726 |
 1 1 |
 2 2 |
 3 3 |
 4 4 |
 5 5 |
‖Δ ‖ ‖
| |
| 真值 | 1 | 1 | 1 | 1 | 1 | / |
| LS | 0.946 093 655 | 1.093 801 465 | 0.970 298 037 | 0.986 810 384 | 1.066 541 909 | 0.131 105 328 |
| fast-WTLS | 0.960 154 916 | 1.071 157 298 | 0.994 505 507 | 0.997 673 115 | 1.050 579 762 | 0.096 150 444 |
|
fast-WTLS结合 Helmert-VCE | 0.966 018 915 | 1.063 779 361 | 0.995 815 997 | 1.000 280 826 | 1.047 417 512 | 0.086 536 271 |
|
图 3 线性参数估计迭代计算过程中两
个方差分量估计值
Fig. 3 Estimates of Two Variance Factors and and  of Linear Parameter Estimation Model over
Different Iteration Steps of Linear Parameter Estimation Model over
Different Iteration Steps
|
从表 4和表 6中可以看出,在普通直线拟合和线性参数求解中使用本文算法进行求解,拟合的结果比fast-WTLS、LS方法拟合的结果都要好。在本文提出的方法中,不仅考虑到系数矩阵中某些元素是常数,不存在误差,而且考虑到各元素之间是不等精度的,以及各元素之间存在相互联系,同时又考虑到不同类型观测值的验前方差一般都很难精确估计,这样就无法给观测向量和系数阵进行精确定权,采用随机模型验后估计方法,能够解决这些问题。所以采用本文方法解算的结果更加接近真值,也更为合理。
3 结 语在线性模型参数估计中随机模型的验后估计应用很广泛,本文提出的加权总体最小二乘随机模型的验后估计分为两部分内容,第一部分是针对函数模型参数的求解;第二部分针对观测向量 y 和系数矩阵 A 的方差分量的求解,因此引入了随机模型的验后估计方法,对观测向量和系数矩阵进行权的重新分配,直至它们所对应的方差分量相等。本文算法推导过程依托了间接平差中赫尔墨特方差分量估计的原理,其优点为可以利用其理论体系中已有的公式推导适用于EIV模型的精度评定和求解自由度的公式,但同时也会继承其缺点。由于算法结构的特点,求解方差分量的迭代过程会出现不收敛,或虽然收敛但是出现负方差分量的情况;本文所模拟的实验仅考虑观测向量 y和系数矩阵A 相互独立的情况,并且假设协因数阵均为对角阵,相关情况未进行数值模拟实验,这两点无疑对本文方法的适用范围进行了限制,今后会针对这两方面做进一步工作。
| [1] | Shi Chuang, Li Min, Lou Yidong, et al. Near Real-time Orbit Determination of Navigation Satellite Using RegionalTracking Network[J]. Geomatics and Information Science of Wuhan University, 2008,33(7):697-700(施闯,李敏,楼益栋,等.利用区域基准站进行导航卫星近实时精密定轨研究[J].武汉大学学报·信息科学版,2008,33(7):697-700) |
| [2] | Zhao Qile, Geng Tao, Li Junyi, et al. Regional Orbit Determination of Navigation Satellite Based on Priori Orbit Constraint Information[J]. Journal of Geodesy and Geodynamics, 2009,28(5):81-84(赵齐乐,耿涛,李俊义,等.历史轨道约束信息下的区域站GPS卫星轨道确定[J].大地测量学与地球动力学,2009,28(5):81-84) |
| [3] | Chen Hui, Du Ruilin, Zhao Qile, et al. Research on Orbit Determination of GPS by Use of Regional Network[J]. Journal of Geodesy and Geodynamics, 2011,31:86-89(陈慧杰,杜瑞林,赵齐乐, 等.利用区域跟踪网进行GPS定轨研究[J].大地测量学与地球动力学,2011,31:86-89) |
| [4] | Zhou Shanshi, Hu Xiaogong, Wu Bin, et al. Analysis of Precise Orbit Determination and Prediction Accuracy Based on Regional Tracking Network[J]. Sience China, 2010(40):800-808(周善石,胡小工,吴斌,等.区域监测网精密定轨与轨道预报精度分析[J].中国科学, 2010(40):800-808) |
| [5] | Geng Tao, Zhao Qile, Liu Jingnan, et al. Regional Orbit Determination of Navigation SatelliteBased on Global Priori Information[J]. Geomatics and Information Science of Wuhan University, 2010, 35(4):491-494(耿涛,赵齐乐,刘经南,等.具有先验信息的区域增强系统卫星轨道确定方法[J].武汉大学学报·信息科学版,2010,35(4):491-494) |
| [6] | Ge M, Gendt G, Dick G, et al. Improving Carrier-Phase Ambiguity Resolution in Global GPS Network Solutions[J]. J Geod, 2005, 79:103-110 |
| [7] | Dong D, Bock Y. Global Positioning Systemnetwork Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California[J]. J Geophys Res, 1989, 94:3949-3966 |
| [8] | Blewitt G. Carrier Phase Ambiguity Resolutionfor the Global Positioning Systemapplied to Geodetic Baselines up to 2000km[J]. J Geophys Res,1989,94:10187-10203 |
| [9] | Mervart L. Ambiguity Resolution Techniques in Geodetic and Geodynamic Applications of the Global Positioning System[D]. Berne:University of Berne, 1995 |
| [10] | Kuang D, Bar-sever Y E, Bertiger W I, et al. GPS-assisted GLONASS Orbit Determination[J]. Journal of Geodesy, 2001,75:569-574 |
 2016, Vol. 41
2016, Vol. 41



 ,得[
,得[