文章信息
- 楼益栋, 姚秀光, 刘杨, 郑福
- LOU Yidong, YAO Xiuguang, LIU Yang, ZHENG Fu
- 模糊度固定与弧段长度对区域站定轨的影响分析
- Impact of Ambiguity Resolution and Arc Length on Regional Precise Orbit Determination
- 武汉大学学报·信息科学版, 2016, 41(2): 249-254
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 249-254
- http://dx.doi.org/10.13203/j.whugis20140201
-
文章历史
- 收稿日期: 2014-09-27

2012年12月27日,我国北斗卫星导航系统正式提供亚太区域服务,2020年将提供全球导航定位服务。精确的卫星轨道是实现高精度导航定位服务的前提条件,而导航卫星定轨精度与地面站连续跟踪观测密切相关。考虑到政治、外交等因素,我国北斗卫星导航系统难以实现境外全球布站,地面跟踪站主要分布在我国境内。因此,对卫星导航系统中贡献最大的中轨轨道(medium Earth orbit,MEO)卫星很难实现全弧段跟踪观测,将影响其轨道精度。虽然,增加星间链路观测是克服地面站不能全弧段跟踪对轨道精度影响的手段之一,但目前地面站跟踪观测仍然是主要手段,如何提高区域站观测情况下的MEO卫星定轨精度是值得研究的问题。
区域跟踪站网覆盖范围有限,对MEO卫星不能实现全弧段跟踪,出境状态下几何观测信息没有对轨道的初始状态及动力学信息形成有效的修正,卫星入境后,由于几何观测条件不强以及待估参数之间的相关性,待估参数需要一段时间收敛,如果入境有效连续观测时段不长,其对动力学信息的修正效果很有限,甚至完全不起作用。与全球网单天快速精密定轨方法不同,区域站定轨通常采用3天跟踪弧段伪距与相位观测值联合解或者对3个单天法方程进行综合的方法[1, 2, 3]。在北斗区域定轨中,周善石等提出对部分轨道参数采用先验信息强约束提高定轨精度,预报1天轨道的URE精度优于0.6 m[4]。耿涛采用全球网确定的参数或预报轨道作为先验信息,通过增加先验约束或虚拟观测值,改善区域站近实时定轨精度[5]。以上方法的本质是通过其他手段精化初始轨道、轨道动力学参数,并作为先验约束信息对轨道参数估计进行强约束,削弱区域网几何观测条件不足对轨道参数估计的影响。然而,该方法实际上同时削弱了实测数据对轨道参数的修正作用,本文提出通过区域网模糊度整数固定,选择合理的观测弧段长度,提高区域定轨解的强度与精度。并且采用中国区域监测站网的GPS观测数据,验证分析了模糊度固定以及观测弧长合理选择对区域站定轨的效果。
1 区域站定轨模糊度固定方法区域站定轨中本文采用网解模式对整网模糊度进行固定[6, 7, 8, 9, 10],方法如下。
1) 将区域观测网中的非差无电离层组合模糊度组成双差模糊度,以模糊度固定数最大化为准则,选择独立双差模糊度。
2) 将剔出了粗差与周跳的干净的相位与伪距观测值,采用Melbourne-Wübbena (MW)组合方法得到观测时段的宽巷模糊度估计值与方差,并组成宽巷双差模糊度。采用模糊度固定判定函数(式(2))进行检验,确定模糊度是否能固定。
3) 将能固定的宽巷模糊度与参数估计得到的无电离层组合模糊度组合,得出窄巷模糊度的估计值与方差。再与固定宽巷模糊度一样,采用模糊度固定判定函数(式(2))进行检验,确定模糊度是否能固定。
4) 对宽巷与窄巷都能固定的模糊度,用固定的整数根据式(1)得到固定的无电离层组合的双差模糊度:

5) 将固定的无电离层组合双差模糊度引入法方程,提高估计参数的精度(包括未固定的模糊度参数)。
重复1)~5)步,直至没有新的模糊度可以固定为止。
模糊度固定判定函数[2]表示为:
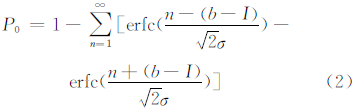
式中,
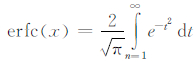
b与σ2是模糊度的估值与方差;I是最接近于b的整数。通常给定模糊度固定的置信度水平a为 0.1%,当P0大于1-a时,将模糊度参数b固定到整数I;反之,模糊度不固定。
2 验证分析本文采用2013年2月9日至17日中国大陆构造环境监测网络观测数据,基于武汉大学PANDA软件,进行GPS全星座区域定轨验证。解算参数包括各卫星轨道参数、卫星钟差、接收机钟差以及对流层参数,采用的观测模型和动力学模型参见文献[1]。验证分析包括:① 不同测站分布情况下,模糊度固定对区域定轨精度影响。该验证采用陆态网络7、17、27、50个测站分布4种方案,测站选择考虑最大覆盖与分布均匀特性(如图 1所示),每种方案均采用3天弧段解算。② 不同轨道弧长情况下,模糊度固定对区域定轨精度影响。采用24 h~72 h弧长,每增 加6 h为一种验证方案,一共9种方案。定轨结果与IGS事后精密轨道比较,统计10 d的全弧段(包括区域不可视弧段)以及区域站在视弧段的三维与径向精度。

|
| 图 1 区域定轨测站(7、17、27、50站)分布图 Fig. 1 Station Distribution Map (7、17、27、50 Station) in Regional Orbit Determination |
图 2给出了验证分析①中区域定轨模糊度固定解(AMB_FIX标记)与浮点解(AMB_FLOLAT标记)的定轨精度统计结果,其中图 2为全弧段定轨精度统计、图 2(a)为在视弧段定轨精度统计。从图 2(b)中可以看出,随着测站数的增多,区域定轨浮点解定轨精度无论是全弧段还是可视弧段统计均有提高:27站相比17站、7站有显著的提高;而50站比27站提高有限,精度趋于一 致,全弧段三维(3D)精度只能达到25 cm左右。对不同测站分布方案的区域定轨 进行整网模糊度固定,统计每种方案固定成功率基本一致,均在90%以上。分析不同方案的区域定轨固定解精度,7站、17站、27站与50站精度相当,比对应分布的浮点解精度(3D)分别提高43.4%、41.7%、35.3%、34.4%;尤其7站的区域定轨精度全弧段3D统计达到21.3 cm,与27、50站相比分别仅差3 cm、5 cm,径向(R)更为接近,仅为1 cm左右。同时,7站的固定解比27站的浮点解三维精度提高6 cm左右,与50站的浮点解相比也提高4 cm左右。以上分析验证了模糊度固定可以显著提高区域站定轨的精度,并减少区域定轨对测站数量的要求,作用明显。

|
| 图 2 不同测站分布的区域定轨精度统计 Fig. 2 Regional Orbit Determination Accuracy Based on Different Station Distribution |
1) 不同观测时长对区域站定轨固定解精度影响分析。限于篇幅,图 3仅给出17站分布情况下从24~72 h每隔6 h为1种方案,共9种方案的模糊度固定解精度统计, 其中图 3(a)为全弧段定轨精度统计,图 3(b)为在视弧段定轨精度统计。验证中的测站平均间距为644 km,9种不同方案的整网模糊度固定成功率在92%~93.4%之间,差别很小。从图 3中可以看出,采用单天(24 h)定轨时,对全星座所有卫星进行全弧段统计,3D精度为4.5 m,R方向精度为1.2 m。这是因为24 h区域观测的有效观测数据少,部分卫星有效观测数据仅为8 h,并且区域跟踪站对各卫星的覆盖不均,导致不同卫星之间的定轨精度相差很大。图 4给出了24 h弧段定轨时,不同卫星的定轨精度统计,其中最差卫星(G18)精度为21.5 m,最好卫星(G12)精度优于0.5 m。图 3中随着时长的增加,区域定轨精度也随着提高:从24 h增加到48 h,精度提高非常显著,全弧段的三维精度和径向精度均提高94%,可视弧段的三维精度和径向精度分别提高92%与89%;从48 h增加到72 h,区域定轨全弧段与可视弧度的精度都趋于稳定,尤其径向精度提高不足1 cm。

|
| 图 3 不同观测时长的区域定轨精度统计 Fig. 3 Regional Orbit Determination Accuracy Based on Different Session Length |

|
| 图 4 24h弧段各卫星区域定轨精度统计 Fig. 4 Orbit Determination Accuracy of Whole Constellation Based on 24 Session Length |
2) 时长不同对全弧段与可视弧段轨道精度差异的影响分析。当时长为24 h时,可视弧段三维精度比全弧段高230.1 cm;当时长大于48 h,两者的精度差异显著减小,48 h与72 h三维精度仅高7.8 cm、3.3 cm,径向精度基本一致。由此说明:随着区域站定轨时长增加,卫星全弧段轨道与可视弧段轨道之间的精度差异显著减少,当时长大于48 h时,两者无显著差异。分析原因,随着观测时长的增加,不可视弧段在多数情况下将位于两段可视弧段之间,两端可视弧段观测数据对中间不可视弧段的轨道参数形成有效修正,因此可以显著提高全弧段的定轨精度。
从以上分析可以看出,观测时长对轨道精度的影响与连续跟踪观测的时间长度相关。如果连续观测弧段太短,影响几何参数(包括卫星钟差、接收机钟差、对流层参数)收敛,将对轨道参数修正不起作用,可视为无效的观测弧段。本文对给定观测时长内,每个卫星对应的多个有效连续观测组成的最长弧段称为该卫星的区域定轨有效弧段。实际上,区域定轨的有效弧段通常包含了可视与不可视弧段,在区域站分布确定情况下,与卫星轨道分布密切相关。
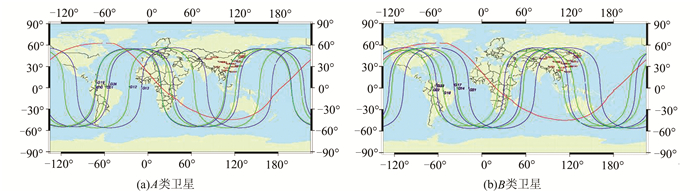
结合上述算例进一步细化分析有效弧段对卫星定轨精度影响。图 5给出GPS不同卫星在一个回归周期内的星下点轨迹以及区域站对观测弧段的覆盖范围。蓝色与青色曲线为卫星的星下点轨迹,红色以北为中国区域站(17站)5°截止高度角的可视范围。因此星下点轨迹分布在红线以北,为卫星的可视区域。GPS卫星区域可视情况可以分为两种不同的特征类型。A类如图 5(a)所示,在一个回归周期内无法形成一个连续观测的可视弧段,一般出现两个弧段观测;B类如图 5(b)所示,在一个回归周期内可以而仅形成一个有效连续观测的可视弧段。A类与B类卫星星下点轨迹主要由轨道面升交点赤经与同一轨道面内卫星的相位角决定。图 7给出了GPS星座连续两天的区域站观测弧段,如图所示每个轨道面将至少存在一颗卫星为B类卫星,如G15(F)、G14(F)、G18(E)、G22(E)、G04(D)、G02(D)、G17(C)、G16(B)、G28(B)、G31(A)。
|
| 图 5 不同卫星星下点分布及在区域可视图 Fig. 5 Track of Subsatellite Point and Visible Coverage |

|
| 图 7 不同轨道面各卫星可视弧段分布图 Fig. 7 Visible Arc on Different Orbit Plane |
本文选择A类卫星G12、G24,B类卫星G18、G31为例分析观测弧段选择对区域定轨的影响。采用2013-02-09 00:00开始一周的观测数据,以24 h作为定轨窗口,每隔1 h向后滑动定轨窗口进行区域定轨,图 6给出了4颗卫星168(7×24)个定轨窗口的定轨精度统计。

|
| 图 6 G12、G24、G18和G31时间序列图 Fig. 6 Time Series of G12、G24、G18 and G31 |
从图 6可以看出,相同的观测时长条件下,不同的观测时段对不同类型卫星的区域定轨精度具有明显差异:A类卫星(如G12、G24)的定轨精度绝大部分时段都优于2 m,最优时段精度优于0.3 m;而B类卫星(如G28、G31)的定轨精度在不同时段之间的差异很大,最差弧段达到25 m左右,最优弧段为0.3 m左右。分析原因,A类卫星不同滑动窗口内的区域定轨有效弧段之间的差异比B类卫星要小的多,如图 7所示,G12(A类)最短有效时间为14 h,最长有效时间为24 h;G18(B类)最短有效时间8 h(为一个连续观测弧段),最长有效时间24 h,并且时段窗口分别滑动到每天的6时,将G18连续可视弧段分为前后两个4 h弧段,两个间隔的前后弧段形成了24 h的有效弧段,卫星定轨精度达到最优。
由于A类卫星与B类卫星在滑动窗口区域定轨中,可以获取的最长有效定轨弧段基本一致,因此不论是A类卫星还是B类卫星所能达到的最优精度基本一致,图 8给出每个轨道面上各卫星在168个24 h区域定轨中最优弧段的定轨精度,三维精度绝大部分优于0.3 m。

|
| 图 8 各卫星的最佳弧段定轨精度图 Fig. 8 Regional Orbit Determination Accuracy of Whole Constellation Based on the Optimum Acrs |
整网模糊度固定可以有效提高区域定轨精度,本文采用国内不同测站分布不同弧长区域定轨的整网模糊度固定成功率在90%以上,平均精度提升幅度在38%左右。仅采用7个区域站的固定解全弧段三维定轨精度达到21 cm,可视弧段三维精度为16.8 cm,与27站(测站数多3倍)固定解定轨精度基本一致,均优于27站浮点解定轨精度。
通过观测时长对区域定轨固定解的影响分析得出:区域定轨精度随着观测时长增加而提高,48 h观测时长比24 h定轨精度有显著的提高,48 h与72 h之间定轨精度接近,72 h比24 h提高95.6%。从全弧段和可视弧段精度统计分析得出:随着时长增加,两者精度差异逐步减小,采用72 h时长两者基本一致。
从卫星星座的构型与地面站可视范围方面,进一步分析了观测时长对不同类型卫星的影响,对在一个回归周期内可以而仅形成一个有效连续观测弧段的卫星,观测时段选择对定轨精度的差异性更大。当观测时间长度达到48 h时,每颗卫星总能获取不小于24 h的最佳有效定轨弧段,定轨精度均可达到0.3 m左右。
| [1] | Shi Chuang, Li Min, Lou Yidong, et al. Near Real-time Orbit Determination of Navigation Satellite Using RegionalTracking Network[J]. Geomatics and Information Science of Wuhan University, 2008,33(7):697-700(施闯,李敏,楼益栋,等.利用区域基准站进行导航卫星近实时精密定轨研究[J].武汉大学学报·信息科学版,2008,33(7):697-700) |
| [2] | Zhao Qile, Geng Tao, Li Junyi, et al. Regional Orbit Determination of Navigation Satellite Based on Priori Orbit Constraint Information[J]. Journal of Geodesy and Geodynamics, 2009,28(5):81-84(赵齐乐,耿涛,李俊义,等.历史轨道约束信息下的区域站GPS卫星轨道确定[J].大地测量学与地球动力学,2009,28(5):81-84) |
| [3] | Chen Hui, Du Ruilin, Zhao Qile, et al. Research on Orbit Determination of GPS by Use of Regional Network[J]. Journal of Geodesy and Geodynamics, 2011,31:86-89(陈慧杰,杜瑞林,赵齐乐, 等.利用区域跟踪网进行GPS定轨研究[J].大地测量学与地球动力学,2011,31:86-89) |
| [4] | Zhou Shanshi, Hu Xiaogong, Wu Bin, et al. Analysis of Precise Orbit Determination and Prediction Accuracy Based on Regional Tracking Network[J]. Sience China, 2010(40):800-808(周善石,胡小工,吴斌,等.区域监测网精密定轨与轨道预报精度分析[J].中国科学, 2010(40):800-808) |
| [5] | Geng Tao, Zhao Qile, Liu Jingnan, et al. Regional Orbit Determination of Navigation SatelliteBased on Global Priori Information[J]. Geomatics and Information Science of Wuhan University, 2010, 35(4):491-494(耿涛,赵齐乐,刘经南,等.具有先验信息的区域增强系统卫星轨道确定方法[J].武汉大学学报·信息科学版,2010,35(4):491-494) |
| [6] | Ge M, Gendt G, Dick G, et al. Improving Carrier-Phase Ambiguity Resolution in Global GPS Network Solutions[J]. J Geod, 2005, 79:103-110 |
| [7] | Dong D, Bock Y. Global Positioning Systemnetwork Analysis with Phase Ambiguity Resolution Applied to Crustal Deformation Studies in California[J]. J Geophys Res, 1989, 94:3949-3966 |
| [8] | Blewitt G. Carrier Phase Ambiguity Resolutionfor the Global Positioning Systemapplied to Geodetic Baselines up to 2000km[J]. J Geophys Res,1989,94:10187-10203 |
| [9] | Mervart L. Ambiguity Resolution Techniques in Geodetic and Geodynamic Applications of the Global Positioning System[D]. Berne:University of Berne, 1995 |
| [10] | Kuang D, Bar-sever Y E, Bertiger W I, et al. GPS-assisted GLONASS Orbit Determination[J]. Journal of Geodesy, 2001,75:569-574 |
 2016, Vol. 41
2016, Vol. 41


