文章信息
- 马晶, 李全, 应玮
- MA Jing, LI Quan, YING Wei
- 基于小波变换的武汉市城乡边缘带识别
- Identification of a Rural-urban Fringe Based on Wavelet Transform-A Case Study of Wuhan
- 武汉大学学报·信息科学版, 2016, 41(2): 235-241
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 235-241
- http://dx.doi.org/10.13203/j.whugis20140053
-
文章历史
- 收稿日期: 2015-02-26

2. 北京大学城市与环境学院, 地表过程分析与模拟教育部重点实验室, 北京, 100871;
3. 武汉大学地理信息系统教育部重点实验室, 湖北武汉, 430079
2. Laboratory for Earth Surface Processes, Ministry of Education, College of Urban and Environment Sciences, Peking University, Beijing 100871, China;
3. Key Laboratory of Geographic Information System, Ministry of Education, Wuhan University, Wuhan 430079, China
城乡边缘带(又称城市边缘区、城乡结合部、城乡交错带等)是指处于主城区与郊区之间的,在土地利用、人口、社会、经济等方面同时受到主城区和郊区的影响,土地利用由城市性质向乡村性质过渡,土地利用方式丰富、结构复杂的带状区域。城乡边缘带的空间范围由内边界和外边界共同决定,其内边界是与主城区的交界线,外边界是与郊区乡村的交界线。对城乡边缘带的空间识别是开展这一城市化进程中最为敏感区域特征研究的基础和前提,能有效支持城镇区域规划、动态监测及土地利用政策制定。
国外学者认为城乡边缘带是城镇与乡村之间极具动态、极端多样的模糊地带,在其内部的多尺度时空上,会出现反复的、较为无序的开发过程,其空间范围受不同解释的主观影响较大[1, 2]。在最初主要凭借经验值划定城乡边缘带的定性分析阶段后,诸多指标及定量方法被应用于边缘带空间范围的界定。近十年来,研究者涉及的主要指标包括Friedberger的日常通勤范围[3],Sudhira的不透水表面指数、人口数据、夜间灯光指数[4],LeSage的郊区新建住宅选址[5]等。Cécile还将分形几何用于大都市物理边界的确定,基于空间不连续性和距离阈值确定城市形态边界[6]。
我国学者在城乡边缘带空间识别研究上,早期主要是以行政边界定性界定为主,定量研究方法则自20世纪90年代中期开始成为主流,陆续使用了阈值判定、突变检测、断裂点分析和空间聚类等多种方法模型解析城乡差异,从而实现城乡边缘带的识别。阈值判定法是城乡边缘带识别的重要方法。钱紫华[7]采用城市用地比例,通过分析其数值水平的分布和变化特征,基于阈值判定思想,划定了西安城市边缘区的范围;程连生等[8]基于信息熵原理,计算北京城市土地利用景观紊乱度,通过熵值剖面图上的高低熵值转折点划分阈值区间,确定内外边界;王秀兰等[9]计算表征景观混乱度的信息熵,以及土地利用程度综合指数,设定阈值确定城乡边缘带范围。阈值判定方法直观易懂,但阈值的设定多通过反复试验得到,极大地影响了识别效率以及识别结果的纵向可比性,且对实验结果的合理性缺乏科学判定。相比之下,突变检测或断裂点分析则具有更高的数学严谨性。陈佑启[10]率先将“断裂点”分析法引入界定城乡交错带边界,根据统计资料计算5类20个指标在可达性衰减区间的变化率及距离衰减突变值,最后通过直接对比各区间衰减突变值的大小,划分出城乡交错带的内、外边界;张宁等[11]基于断裂点理论,使用建设用地比率指标划分了北京城乡过渡带;赵华甫等[12]通过找出每个土地利用动态度剖面线由低值到高值和由高值到低值的转折点,描绘出城乡交错带内外边界的位置;章文波等[13]则引入均值突变检验方法中的滑动t检验方法检测城市用地比率变化转折点的空间位置,进而根据突变点的空间分布确定城乡边缘带内、边外界的位置。除突变检测之外,一些模型及空间聚类的方法也被广泛应用在边缘带识别上,特别是王海鹰等[14, 15]采用K-means空间聚类方法,处理基于拟合的Logistic模型计算的各空间单元“城市化特征属性值”,将城市划分为城市核心区、城乡边缘带及城市影响区。这些方法,为城乡边缘带的识别拓宽了思路。
综合来看,现有研究的主要特征和不足是:① 指标选取过于繁琐,且对统计数据依赖较大,导致指标设计及空间定位不灵活;② 大部分识别方法主观性和经验性较强,不利于识别方法的复制重建及结果的纵向比对;③ 绝大多数方法都是针对内、外边界分别提取,导致识别效率较低。
本文在对土地利用程度综合指数与城乡边缘带的关系进行理论及样带分析的基础上,将具有对输入信号多尺度分解和重构能力的广泛应用于地理现象突变分析的小波变换方法引入城乡边缘带识别研究中。以遥感影像为基础数据,选用土 地利用程度综合指数模型定量评价土地利用程度,基于小波模极大值检测原理,检测由综合指数数据序列变换得到的小波系数突变点群,依据突变点群的空间格局一次性识别城乡边缘带内、外边界。本文方法有望提高城乡边缘带的识别效率,减少方法的主观臆断性,实现识别结果间的比较。
1 研究方法武汉市位于北纬29°58′~31°22′,东经113°41′~115°5′。行政划辖区13个,其中7个中心城区,6个郊区。武汉市作为中部地区的特大城市和中部崛起的领军城市,在过去的10余年时间里经历了快速城市化。从2000年~2011年,武汉建成区面积由210 km2扩大至507 km2,城市户籍人口由441万增至827万人。
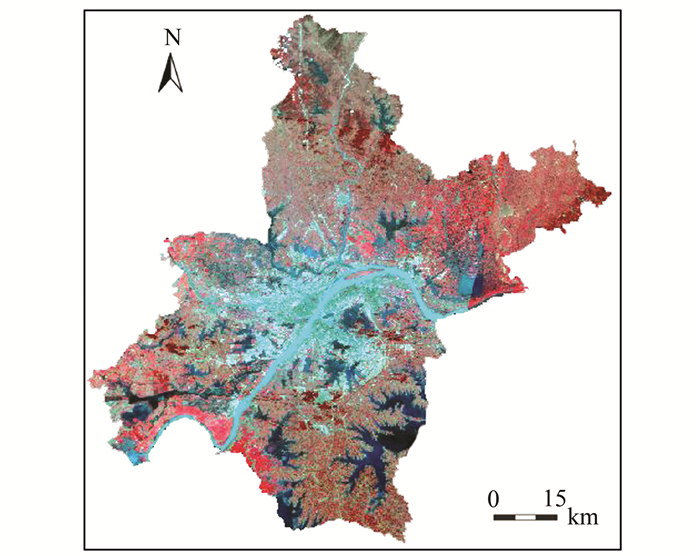
本文采用中国科学院计算机网络信息中心国际科学数据服务平台的2010年9月获取的四景覆盖武汉市Landsat ETM+影像作为基础数据。对获取的影像进行镶嵌、配准和裁剪等预处理工作,结果如图 1。
|
| 图 1 武汉市2010年LANDSAT ETM+影像(标准假彩色合成) Fig. 1 LANDSAT ETM+ Image of Wuhan in 2010 (Composed by Standard False Color) |
土地利用程度综合指数模型(land use degree comprehensive index ,LUDCI)已广泛用于城市土地利用程度的定量评价。该模型将土地利用状态定为4种土地利用级,未利用土地级为1级,2、3级分别为林、草、水用地级和农业用地级,城镇聚落用地级为4级。LUDCI计算公式为:
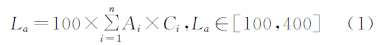
式中,La是土地利用程度综合指数;Ai是第i级的土地利用程度分级指数;Ci是第i级土地利用程度分级面积百分比。
土地利用程度综合指数的数值大小表示某一地区土地利用程度的高低。数值越大,土地利用程度越高,该地区社会经济活动越复杂、越接近城市;相反,则土地利用程度越低,社会经济活动越简单,越接近乡村。因此,土地利用程度综合指数可以作为界定城乡边缘带的依据。
1.2 基于空间小波变换的突变点检测小波变换通过小波与待分析函数f(t)“相乘”(内积)达到分解原函数的目的。其含义是把某一称为基本小波的函数ψ(t)位移τ后,再在不同尺度a下与待分析函数f(t)作内积,如式(2):
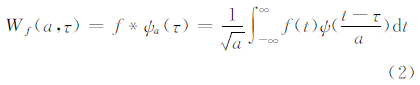
经过基本小波与待分析函数作内积之后,可分解到不同尺度下的小波系数。这一过程就是小波变换。如果地理空间某一要素空间采样成的数据序列为S(x),则与时间域小波变换类似,空间连续小波变换(spatial continuous wavelet transform,SCWT)如式(3):
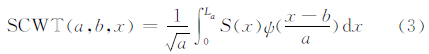
式中,a 为尺度因子,τ为平移因子,C 为小波系数。
若取ψ(1)(t)为光滑函数的一阶导数,ψ(2)(t)为光滑函数的二阶导数,与具有阶跃奇异性的信号f(t)作小波变换。由于ψ(1)(t)和ψ(2)(t)的局部奇偶性,将它们与信号做内积之后,使得信号的突变点对应于Wf(1)(a,t)的模极大值点,对应于Wf(2)(a,t)的过零点,但ψ(2)(t)的过零点并不都是突变点,所以,在突变检测中,取光滑函数的一阶导数作为小波母函数将信号作小波变换,则小波变换的模极大值点对应于信号突变点的位置。需要指出的是,小波函数的尺度a越小,小波变换的模极大值点与信号突变点的位置对应关系越准确。但由于小尺度下的小波变换系数易受噪声影响,可能会产生伪极值点,而在大尺度下,在对信号进行磨光处理的同时,噪声也得到了磨光处理,故极值相对稳定,但磨光处理也导致极值点定位相对较差。因此,在利用小波变换模极大值检测突变点时,需要多尺度综合分析才能获得最佳效果。
1.3 城乡边缘带识别方法从理论上分析,由于主城区以接连成片的建设用地为主,其土地利用程度综合指数统一处于较高水平且数值分布平稳;郊区乡村以连绵的农用地为主,土地利用程度指数统一处于较低水平,且均质性较好;而城乡边缘带土地利用由城市性质向乡村性质过渡,土地利用类型复杂,结构零碎,故其综合指数值应介于两者之间,且会表现出奇异性,具有突变的性质。
因此,土地利用程度综合指数沿城乡断面存在突变点群且大量分布于城乡边缘带内,从市中心向外,开始出现突变点群的圈层就是城乡边缘带的内边界,突变点群消失的圈层则是城乡边缘带的外边界,突变点群的空间格局即对应于城乡边缘带的空间格局。对研究区几条样带的分析佐证了这一结论。因此,通过检测城乡断面上土地利用程度综合指数的突变点的位置和范围,即可实现城乡边缘带空间位置和范围的识别和定位。
2 武汉市城乡边缘带识别 2.1 土地利用综合程度指数计算
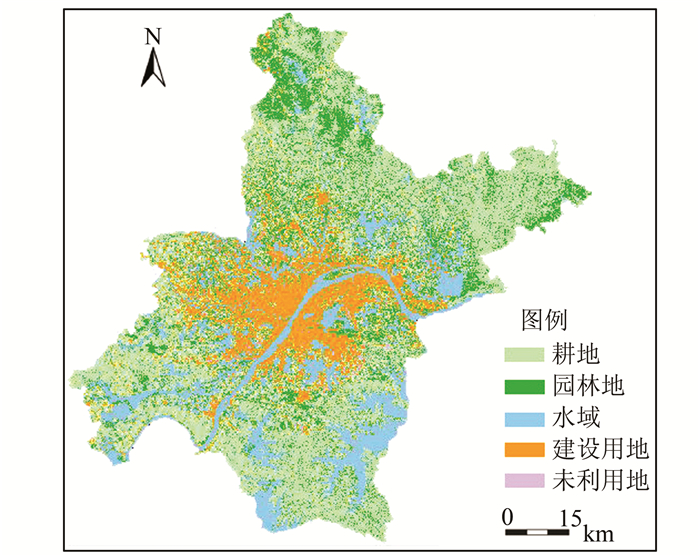
采用最大似然法进行武汉市土地利用/覆盖监督分类,将研究区内土地利用/覆盖划分为耕地、园林地、水域、建设用地和未利用地等五类,分类结果如图 2。分类总精度为87.3%,Kappa值为0.847 6,各类别生产者精度和用户精度在85%以上,达到分类精度要求。
|
| 图 2 土地利用/覆盖监督分类结果 Fig. 2 The Supervised Classification Result of Land Use/Cover |
根据土地利用程度综合指数模型,在此基础上进行土地利用程度综合指数的计算。
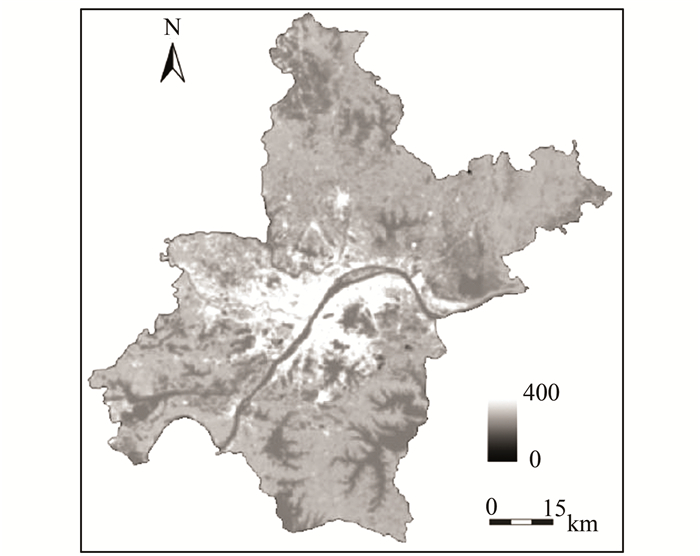
在ERDAS IMAGINE 9.1上利用Model Maker工具建模,计算各土地利用级在30×30窗口(对应地面实际范围900 m×900 m)内所占百分比,并以此计算武汉市域范围内各栅格单元的土地利用程度综合指数,得到武汉市2010年土地利用程度综合指数灰度分布图如图 3。
|
| 图 3 土地利用程度综合指数灰度分布 Fig. 3 The Spatial Distribution of LUDCI Use/Cover |
地理要素的空间分布是连续的,与过程分析一样,在实际计算时需要进行空间重采样。为剔除随机变化的影响,突出土地利用程度综合指数圈层变化的总体特征,采用经过多次试验确定的20×20平滑窗口获得该窗口内土地利用程度综合指数的平均值,利用ArcGIS的zonal statistics as tables命令,将窗口中心像元值输出至文本文件中。
在平滑图像上选取武汉市的中心点作为原点,从图像的四周边缘线逐采样单元向原点做连线,每条连线经过的采样单元构成一个样带数据序列,然后对所得的数据序列集逐个进行突变点检测。共有119×173=20587个采样单元,覆盖整个研究区,按照上述样带提取方法,上下左右边缘上共有(119+173)×2-4 = 580个采样单元,因此共有580条样带,每条样带都是由一系列600 m×600 m的采样单元构成。
2.2.2 小波系数模极大值检测本研究采用Daubechies(db)小波函数,它们是一类二进制小波,将连续小波变换在尺度上进行了二进制离散,而位移仍取连续变化。二进制小波具有连续小波变换的时移共变性,这是它较之离散小波所具有的连续的独特优点。基于db小波簇中的db3对待分解的对象具有良好的分解、重构和局部定位能力(具有紧支撑集),且国内外普遍采用db3检测奇异点或不连续,故本文选用db3来进行检测。
引入小波方差估测格局和过程的尺度参数。将时间或空间域上的关于尺度a的所有小波系数的平方进行积分,可得到小波方差。事实上,小波方差是按照每一尺度分解格局或过程方差的,因此它能够使我们检测到不同尺度的格局特征或过程行为,以不同尺度和对应的方差作图,即得到小波尺度方差图。通过小波方差图可以看出不同尺度上的变异程度,如果在小波尺度方差图上发现明显的拐点,则说明格局或过程具有显著的尺度域转换。对土地利用程度综合指数进行多尺度分解,最大分解尺度为小波尺度24(由于db3小波的中心频率为0.8,故换算成空间尺度约为30 km,小波尺度与空间尺度的换算公式见式(4),已达到样带长度的四分之一强。

式中,a表示小波尺度,表示采样周期;Fc表示所选小波的中心频率;Fa表示实际尺度。
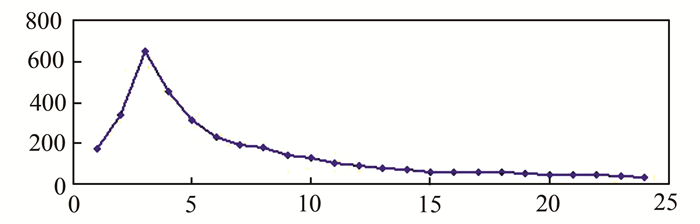
图 4为20×20采样窗口所得到的一条数据样带的小波方差图,所选样带是从中心点向正东方向的一条,先后包括了主城区、边缘带以及郊区的采样单元,并经过了水体,与580条样带中绝大多数样带情况一致。此外,经抽样检验其他样带,与图中小波方差具有基本一致的分布特征。从图 4中可以看出,武汉市土地利用程度综合指数主要尺度域在2~5 db3小波尺度范围内,经过反复试验确定最佳尺度为小波尺度3进行武汉市城乡边缘带的空间识别。
|
| 图 4 样带小波方差图 Fig. 4 Variance of Wavelet in Belt Transect |
对经过空间重采样的数据用db3小波进行尺度为3的小波变换。在MATLAB上首先对空间重采样得到的数据进行距平处理,去掉系列中的趋势和周期成分;然后用db3小波完成小波变换,得到小波系数分布图,通过编程检测各数据序列的模极大值点。
2.3 突变点群空间可视化
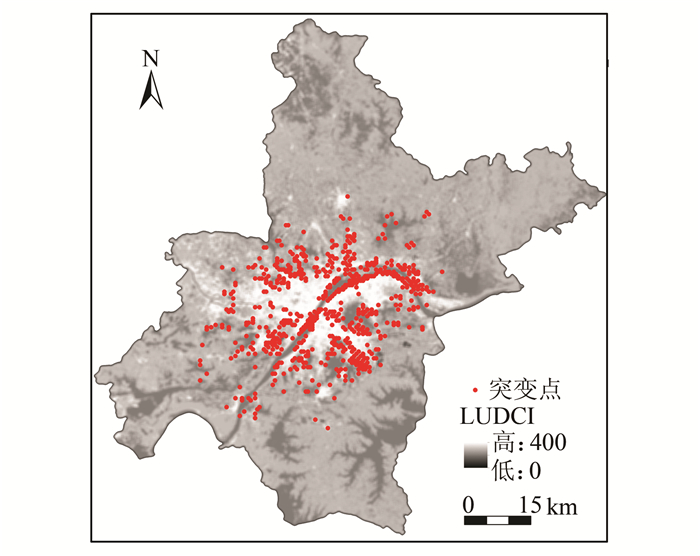
在MATLAB中将突变点以增加属性列的方式增加在采样点文本文件中,然后在ArcGIS中通过属性表的连接将检测到的突变点以点图层的方式导入,图 5为使用db3小波核函数,在小波尺度为3、采样窗口为20×20时检测到的武汉市土地利用程度综合指数突变点群的分布格局。
|
| 图 5 突变点群空间格局 Fig. 5 Spatal Pattern of Mutation Point Group |
从图中可以看出,突变点群的空间格局呈现以下特点:① 突变点群的整体格局表现为围绕着主城区,即土地利用程度综合指数分布图上灰度值较大区域的具有一定宽度的环带状区域;② 突变点群的分布主要集中于两处,一是城乡边缘带的空间范围内,二是武汉市的水域与陆地的交界处,即沿长江、汉江等河流以及东湖等湖泊岸边分布。
后一种突变点群的存在主要缘于武汉市两江交汇、百湖之市的市情,其中的大部分具有严格的数学意义却不具备实际意义,其中经过对比明显位于城区范围,仅由于水陆分界导致的这类突变点在城乡边缘带绘制时需要剔除。
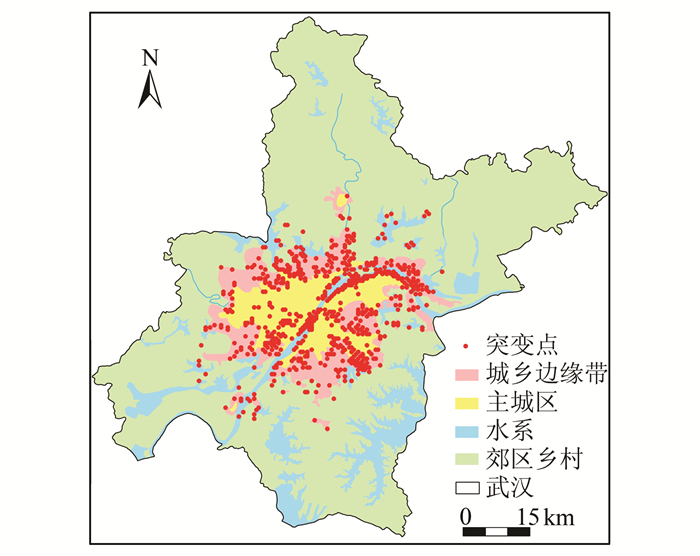
如前文所述,沿城乡断面从市中心向外,土地利用程度综合指数分布图上开始出现突变点的位置对应于城乡边缘带的内边界,突变点群消失的位置对应于城乡边缘带的外边界。以突变点群的空间格局为基础,参照武汉市土地利用程度综合指数分布等值线图,在ArcGIS上实现武汉市城乡边缘带的手动绘制,连接最外层突变点形成外边界,连接最内层突变点形成内边界,结果如图 6。
|
| 图 6 2010年武汉城乡边缘带空间位置及范围 Fig. 6 Spatial Location and Scope of Wuhan Urban-rural Fringe in 2010 |
统计可知,武汉市城乡边缘带的面积约为882.35 km2,占该市总面积的11.1%,主要包括东西湖区中部的大部,黄陂区南部的少部,蔡甸区东部的少部,江夏区北部的少部,洪山区中部的大部以及新洲区南部的少部。城乡边缘带的外部几何形态受市域内湖泊分布影响深远,以长江为界,在主城区东西两侧分布基本均衡,且在西北和东南方向范围较大。
对比武汉市2010年主城区规划用地与本研究基于武汉市2010年Landsat ETM+影像采用小波变换进行突变检测得到的武汉市2010年主城区范围基本一致,且识别得到的武汉市城乡边缘带基本分布在土地利用总体规划2010~2020年的主城区扩展范围内,间接说明识别结果具有较高的合理性。
从景观生态学角度,不同土地利用方式的组合形成不同的景观和景观结构。土地利用过程是自然景观转变成人文景观的过程,景观结构及其发展变化是人类活动和自然环境相互作用的结果。因此,本研究选用斑块所占景观面积比例(percent of landscape,PLAND)以及香农多样性指数(Shannon's diversity index,SHDI)两个景观格局指数,对主城区、郊区和城乡边缘带的地表特 征进行定量统计分析。结果表明,主城区、郊区的SHDI值较小,主城区建设用地的PLAND值接近80%,郊区乡村农耕地和园林地的PLAND值之和接近80%,均质性较好;城乡边缘带各用地类型的PLAND值差别显著 小于城区和郊区,且SHDI值在三区中是最大的,表明其景观多样性最高,景观均质性最低,与前文分析一致。景观格局指数在主城区、城乡边缘带以及郊区乡村的分布特征,证明了本研究识别结果的可靠性及科学性。
3 结 语本文探讨了一种基于土地利用程度综合指数(LUDCI)数据序列,采用空间小波变换模极大值原理检测其突变点群,以识别城乡边缘带空间范围的方法,并以武汉市作为研究区进行了实证分析,得出如下主要结论。
(1) 基于遥感数据,采用土地利用程度综合指数,从数值水平和波动性两方面定量刻画城区、郊区乡村以及城乡边缘带的用地特征,直观、简洁且便于操作。以土地利用为主的空间数据为城乡边缘带的识别带来了更为广阔和细致的研究视角。
(2) 城乡边缘带具有土地利用程度综合指数变化剧烈的显著特征,基于空间小波变换模极大值检测思想,检测土地利用程度综合指数样带的突变点群,可以实现城乡边缘带空间范围的整体识别。将空间小波变换引入土地利用程度指数的突变检测,从方法上增强了城乡边缘带识别的数学严谨性。
(3) 以武汉市为研究区进行实例研究,一次性提取了武汉市城乡边缘带的内、外边界,并对识别结果进行了科学性和合理性检验。研究结果表明,基于土地利用程度综合指数和空间小波变换的城乡边缘带提取方法严谨、高效,可靠性高。
囿于基础数据分辨率限制,未能将土地利用划分至更细致级别,带来土地利用程度指数计算结果的误差,未来可选用多数据源、多分辨率影像互补解译,或者直接利用土地利用矢量数据以提高计算精度;可考虑选取更多的城乡边缘带指示要素,如不透水指数、NDVI、夜间灯光指数等,通过对比试验选取用于城乡边缘带识别的最佳指示要素,以进一步提高识别结果的可信度和准确度;还可进一步系统探索城乡边缘带识别理论体系和方法体系,总结城乡边缘带的演变机制,深化边缘带识别的应用研究,为城乡边缘带识别工作带来新的活力。
| [1] | Rauws W S, De Roo G. Exploring Transitions in the Peri-urban Area[J].Planning Theory & Practice, 2011, 12(2):269-284 |
| [2] | Scott A J, Carter C, Reed M R, et al. Disintegrated Development at the Rural-urban Fringe:Reconnecting Spatial Planning Theory and Practice[J].Progress in Planning, 2013, 83:1-52 |
| [3] | Friedberger M. The Rural-urban Fringe in the Late Twentieth Century[J].Agricultural History, 2000, 74(2):502-514 |
| [4] | Sudhira H S, Ramachandra T V, Raj K S, et al. Urban Growth Analysis Using Spatial and Temporal Data[J]. Journal of the Indian Society of Remote Sensing, 2003, 31(4):299-311 |
| [5] | LeSage J P, Charles J S. Using Home Buyers' Revealed Preferences to Define the Urban-rural Fringe[J]. Journal of Geographical Systems, 2008, 10(1):1-21 |
| [6] | CécileTannier, Isabelle Thomas,Gilles Vuidel, et al. A Fractal Approach to Identifying Urban Boundaries[J]. Geographical Analysis.2011,43(2):211-227 |
| [7] | Qian Zihua, Chen XiaoJian. Spatial Expansion in Urban Fringe of Xi'an[J]. Human Geography, 2005,20(3):54-58(钱紫华,陈晓键.西安城市边缘区空间扩展研究[J].人文地理,2005,20(3):54-58) |
| [8] | Cheng Liansheng, Zhao Hongying. Discussion on the City's Border Area of Beijing[J]. Journal of Beijing Normal University(Natural Science),1995,31(1):127-133(程连生,赵红英. 北京城市边缘带探讨[J].北京师范大学学报(自然科学版), 1995,31(1):127-133) |
| [9] | Wang Xiulan, Li Xuerui, Feng Zhongke. Methods of Urban Fringe Definition in Beijing Based on TM Image[J].Remote Sensing Information, 2010,4:100-104(王秀兰,李雪瑞,冯仲科.基于TM影像的北京城市边缘带范围界定方法研究[J].遥感应用,2010,4:100-104) |
| [10] | Chen Youqi. Discussion on Rural-urban Fringe, its Feature and Function[J]. Economy Geography, 1996,16(3):27-31(陈佑启. 试论城乡交错带及其特征与功能[J]. 经济地理, 1996,16(3):27-31) |
| [11] | Zhang Ning, Fang Linna, Zhou Jie, et al. The Study on Spatial Expansion and Its Driving Forces in the Urban Fringe of Beijing[J]. Geographical Research, 2010,29(3):471-480(张宁,方琳娜,周杰,等.北京城市边缘区空间扩展特征及驱动机制[J].地理研究,2010,29(3):471-480) |
| [12] | Zhao Huafu, Zhu Yuhuang, Wu Kening, et al. Study of the Mothod for the Demarcation of Urban-rural Fringe Based on Land Use Dynamic Indicator[J]. China Land Sciences, 2012,26(9):60-65(赵华甫,朱玉环,吴克宁,等. 基于动态指标的城乡交错带边界界定方法研究[J].中国土地科学,2012,26(9):60-65) |
| [13] | Zhang Wenbo, Fang Xiuqi, Zhang Lansheng. Method of Identify the Urban-rural Fringe by TM Images[J]. Journal of Remote Sensing, 1999,3(3):199-202(章文波,方修琦,张兰生. 利用遥感影像划分城乡过渡带方法的研究[J].遥感学报, 1999,3(3):199-202) |
| [14] | Wang Haiying, Zhang Xinchang, Zhao Yuan. On Determination Methods for Urban Edge Regions Based on Logistic Regression Model[J]. Bulletin of Surveying and Mapping, 2010,10:7-10(王海鹰,张新长,赵元.基于逻辑回归模型的城市边缘区界定方法研究[J]. 测绘通报, 2010,10:7-10) |
| [15] | Wang Haiying, Zhang Xinchang, Kang Tingjun, et al. Urban Fringe Division and Feature Analysis Based on the Multi-criterion Judgment[J]. Journal of Natural Resources, 2011,26(4):703-714(王海鹰,张新长,康停军,等. 基于多准则判断的城市边缘区界定及其特征[J].自然资源学报, 2011,26(4):703-714) |
 2016, Vol. 41
2016, Vol. 41



