文章信息
- 禹文豪, 艾廷华, 杨敏, 刘纪平
- YU Wenhao, AI Tinghua, YANG Min, LIU Jiping
- 利用核密度与空间自相关进行城市设施兴趣点分布热点探测
- Detecting “Hot Spots” of Facility POIs Based on Kernel Density Estimation and Spatial Autocorrelation Technique
- 武汉大学学报·信息科学版, 2016, 41(2): 221-227
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 221-227
- http://dx.doi.org/10.13203/j.whugis20140092
-
文章历史
- 收稿日期: 2014-11-05

2. 天津大学海洋科学与技术学院, 天津, 300072;
3. 数字制图与国土信息应用工程国家测绘地理信息局重点实验室, 四川成都, 610100;
4. 河南理工大学矿山空间信息技术国家测绘地理信息局重点实验室, 河南焦作, 454000;
5. 中国测绘科学研究院, 北京, 100039
2. School of Marine Science and Technology, Tianjin 300072, China;
3. Key Laboratory of Digital Mapping and Land Information Application of National Administration of Surveying, Mapping and Geoinformation, Chengdu 610100, China;
4. Key Laboratory of Mine Spatial Information Technologies, National Administration of Surveying, Mapping and Geoinformation, Henan Polytechnic University, Jiaozuo 454000, China;
5. Chinese Academy of Surveying and Mapping, Beijing 100039, China
城市设施兴趣点(POI)数据描述城市空间中各类工程型与社会性服务设施,蕴含着丰富的人文经济及自然信息,是城市建设管理部门及普通民众关注的热点对象。城市设施的分布受城市环境及人类活动的影响,在局部地理空间下往往呈现聚集型分布特征,如商业中心区的金融设施点、文化中心区的教育型设施点等,利用城市空间分析方法研究城市设施点群的聚集模式,可以为城市发展规划、社会经济结构、商业布局以及民众行为心理等研究提供重要的信息服务[1, 2]。
空间点的聚集分析即热点分析在很多领域都有广泛的应用,如地理学、经济学、流行病学等[3, 4, 5, 6]。根据研究内容的区别,点分布模式的分析方法可以分为两类:① 研究空间过程的一阶属性,即点分布格局的基本属性和过程预期值在空间中的变化特征,如样方分析、核密度估计等;② 研究空间过程的二阶属性,即点在空间分布中的相互依赖特征,如最邻近分析、K函数、Getis-Ord G*i以及局部Moran’s I等[3, 7]。其中,核密度分析易于实现及能较好地反映地理现象空间分布中的距离衰减效应,符合地理学第一定律,是最常用到的热点分析方法[8, 9, 10, 11]。
在传统城市和区域分析中,核密度方法主要是作为一种可视化工具,描述地理现象特征分布的一阶基本属性[4, 11]。通过对密度计算结果的二维灰度表达或三维曲面表达,人们可以简单直观地获取点群的聚集或离散等分布特征。然而该分析过程中缺少量化统计评价 的干涉,即“密度值高于多少是真正意义上的热点”问题的回答。更深层次的量化热点分析需要引入一些合适的局部空间统计方法。
空间统计可用于衡量一个位置上的某种地理现象或某一属性值与邻近位置上同一现象或属性值的相关性[5]。几乎所有空间数据都具有空间依赖或空间自相关特征[12]。早在上世纪九十年代,以Anselin[6]为代表的专家就意识到空间统计在地理现象量化分析中的重要性,并对其进行了一系列探索,提出了大量的空间数据的统计方法。其 中应用最广的有Getis-Ord G*i与局部Moran’s I方法[6, 7]。Getis-Ord G*i是描述局部 空间自相关的统计量,反映了高值或低值聚集的情况,采用Getis-Ord G*i指标可以表达地理现象的二阶分布属性。与以往将自相关技术和核密度估计单独分析不同,本文提出两种方法的融合方法,利用Getis-Ord G*i指标在核密度属性单元的基础上探测城市设施POI的统计学显著热点。
事实上,无论是在核密度方法的基础上定量化分析点群分布,还是从自相关分析的角度考虑信息完整性问题,都表明对两者融合方法研究的必要性。在地理现象分析中,空间统计的基本出发点是空间抽样。传统样方法是将研究区域分割成一系列均匀的子区域(即样方),统计落入各样方的特征值作为样方单元的属性值。样方法会产生一系列问题,如原始数据在空间单元内及单元连接处的信息丢失,以及样方单元形状、维度、方向等特征选择的随意性。针对“由于对连续地理现象的人为划分而产生的空间模式变化”,核密度方法可以较好地解决[10, 11]。与样方法假设划分单元之间无相关关系不同,核密度基于“距离衰减效应”,区域单元获取的属性值(即核密度值)随中心单元辐射距离的增大逐渐变小,分析结果表现出距离越近的事物相关性越大的特征。该方法可以反映地理现象空间分布的信息衰减事实,符合地理学第一定律,而且目前空间自相关分析领域中缺少有关核函数采集单元属性值的应用。
传统空间自相关研究主要是基于样方法来探测空间聚类现象[13, 14, 15, 16, 17, 18]。例如,徐建华等运用空间统计分析方法,以各类景观斑块为单元,研究城市景观格局的空间尺度效应[13];陈江平等利用网格模拟数据和中国人均GDP实例数据,研究空间自相关的可塑性面积单元问题[14]; Swift等所做的有关水质和胃肠疾病的相关性分析虽然考虑了分区方式对分析结果的影响,但是他们仍然以空间单元作为地理现象的影响范围,无法反映地理现象在空间单元间传播扩散的连续性信息[16]。注意到以上问题,国内一些学者开始引入核密度估计进行聚类分析,例如,蒋海宁等分析中国企业的基础分布格局,但在深入的自相关分析部分仍然采用样方法统计行政区域单元的企业个数[19];另外,海贝贝等基于行政单元统计居民点数,以此作为自相关分析的基础数据,探测农村居民点聚集的热点区域[20];马晓东等以乡村聚落地的斑块面积为分析变量,通过Getis-Ord G*i方法测度江苏省乡村聚落的分布特征[21]。尽管核密度估计与自相关分析两种方法已有很多成功案例,但以往的研究均将核密度估计与自相关分析方法区别对待,前者用于点密度的基本分布特征分析,后者则基于样方法重新采集单元内的特征值,以此分析地理现象的自相关特征。
顾及到城市设施服务影响的地理意义,本文拟用核密度方法计算地理单元的城市设施POI群点空间密度值,然后利用带有核密度值的统计单元,引入Getis-Ord G*i统计方法探测城市空间中具有显著统计学意义的POI分布热点。与基于样方法的空间自相关分析方法比较,本文提出的热点探测方法更有效,分析结果更符合城市设施在空间分布上的连续性空间特征和区域型服务模式。
1 POI点分布热点探测热点是由高值对象的地理次序或地理位置造成的,一般来说,高值对象在局部空间内频繁聚集出现可形成热点区域。对于分布热点的分析,核密度法是对空间现象的一种场表达,各地理单元根据其与相邻设施点的空间关系决定单元的点聚集强度,即密度属性值。核密度用于分析空间过程的一阶属性,若引入空间自相关方法计算地理单元分布强度在邻近区域内的显著水平,可以挖掘 深层次的量化信息,特别是在预期空间随机的假设模式下,验证聚类的空间分布特征,如犯罪热点分析、城市区域描述以及经济活动空间分布分析。
1.1 地理单元的点密度聚合方法空间自相关分析前需对设施点数据进行聚合。常用的聚合方式是样方采集方法,利用划分空间的均匀网格来汇总落入其中的点数,如图 1(a)所示。该方法实现简单,但是也会存在以下两个问题: ① 单元连接处的密度变化突兀,忽略了地理现象空间分布的连续性;② 粒度大小与单元划分方法的不确定性会改变甚至忽略点密度数据之间的自相关性。核密度方法可以解决这种由于对连续地理现象的人为划分而引起的问题。地理学第一定律指出:所有事物都是相互联系的,但离 得越近的事物彼此之间的联系就越强。核密度方法的根本出发点正是基于此定律,密度估计值是随中心辐射距离的增大逐渐变小,考虑了设施点对它周围位置服务影响的距离衰减作用。例如,对于图 1(a)中所示的模拟数据,利用核密度聚合方法,我们可以得到图 1(b)所示的更平滑的结果。
核密度估计可以表示为:
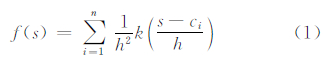
|
| 图 1 样方法和核密度聚合方法的比较示例 Fig. 1 Illustration of Quadrat and Kernel Density Setimation for Clustering |
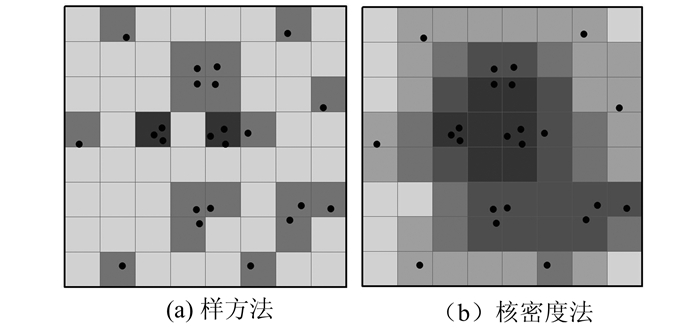
式中,f(s)为空间位置s处的核密度计算函数;h为距离衰减阈值(即带宽);n为与位置s的距离小于或等于h的要素点数;k函数表示空间权重函数。核密度估计存在两个关键参量:空间权重函数k与距离衰减阈值h。研究表明权重函数的选择对分析结果的影响不大,需要注意的是距离衰减阈值的选择[16, 17, 18]。
本文主要采用式(2)所示的四次权重方程,衰减阈值h的确定则取决于以下因素。① 研究的尺度,较大的距离衰减阈值适合于全局视角下设施分布的一般聚类特征,而较小的衰减阈值适合表示点模式的局部特征;② 设施点之间的距离,衰减阈值的大小应与设施数据的离散程度呈正相关关系;③ 设施POI的性质,不同性质设施在空间所表现的特征尺度不一样,如大型商场的服务范围比小型超市的服务范围更大,可以使用较大的影响范围来获取有价值的服务空间分布模式。
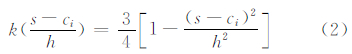
通过比较两种聚合方法发现,核密度估值以一种光滑曲面的形式渐进式传输中心强度,顾及和体现了空间位置的差异性以及中心强度随距离衰减的特性,在城市空间自相关分析中具有更大的应用潜力。
1.2 基于核密度的空间自相关空间自相关是指对象的属性值在空间上的关联关系,相应的指标可用于定量衡量地理空间对象的全局和局部两类特征。研究城市设施POI点的分布热点只考虑局部性指标,即描述每一个空间单元的周围局部区域内某一属性的空间聚集程度。常用的局部度量指标包括有:Local Moran’s I和Getis-Ord G*i等,由于局部Moran’s I仅表示属性相似或相异的观测值空间集聚状况,但并不表示该属性值高低[6, 7]。因此,本文通过测算Getis-Ord G*i统计指数来分析POI集聚热点区域的变化情况,即反映区域上高值或低值的聚集情况,其计算公式为:
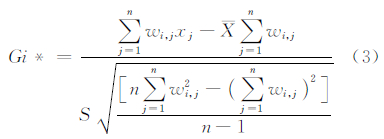
式中,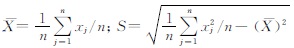 ;xj 是第j个地理单元的点密度值; 是所有单元的密度均值;wi,j是单元i和j的空间权重系数;n 为研究区域内所有单元的总数量。对于空间分布热点研究来说,地理单元可以是区域内的行政分区或格网化后的网格单元,单元的属性取值可以基于传统的样方法,或基于距离衰减效应的核密度计算方法。
;xj 是第j个地理单元的点密度值; 是所有单元的密度均值;wi,j是单元i和j的空间权重系数;n 为研究区域内所有单元的总数量。对于空间分布热点研究来说,地理单元可以是区域内的行政分区或格网化后的网格单元,单元的属性取值可以基于传统的样方法,或基于距离衰减效应的核密度计算方法。
G*i值实际上就是统计学意义上的z得分。本文基于正态分布检验假设,选取显著性检验水平为5%,对应于临界值1.96。因为考虑的参量是地理单元的点密度值,所以实际要找的是高值聚集的区域,亦即z得分大于1.96的单元集合作为热点。另外,注意到核密度计算已经考虑了空间距离对单元属性值的影响,为了方便比较,本文通过以下方式来确定权系数:对于样方法,其自相关分析采用反距离方式,即与单元的距离越近,相应的权重值将越大;而对于核密度,自相关分析采用固定距离范围,即一定距离内的单元权重为1,在距离之外为0。
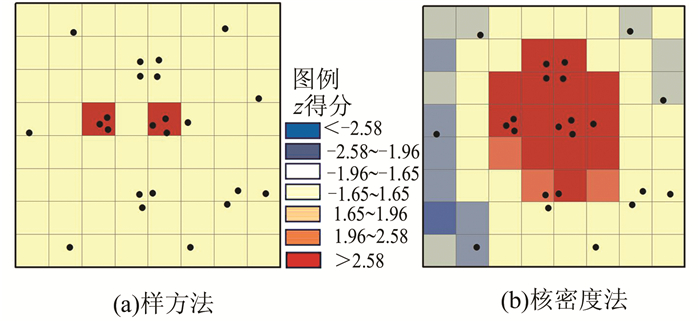
图 2为采用不同聚合方式的G*i值计算结果比较。图 2中,地理单元边长为1 unit,图 2(a)中的反距离阈值以及图 2(b)中的核密度衰减阈值、固定距离阈值均为2 units。如图 2(a)所示,基于样方法计算的数据相关性较弱,并且热点单元比较零散。这是由于设施的影响范围被限制于划分的空间单元内,无法跨越单元边界传导密度值。虽然在G*i值计算中引入反距离方式,但是热点的总体分布还是呈现离散、连续性不强的形态。图 2(b)中所示的数据则具有较强的正相关性,热点区域符合该数据点群的聚类情况。基于核密度方法的自相关分析顾及了地理学第一定律的区位影响,可以获得连续性较好、具有显著统计学意义的热点。因此,在对设施点 数据进行空间自相关分析时,需要慎重考虑因空间单元人为划分所引起的不确定性,采用基于距离衰减效应的量化分析方法更符合连续性地理现象的空间分布特征。
|
| 图 2 基于样方法和核密度法的空间自相关性示例 Fig. 2 Illustration of the Correlation Coefficients Based on the Methods of Quadrat Counting and Kernel Density Estimation |
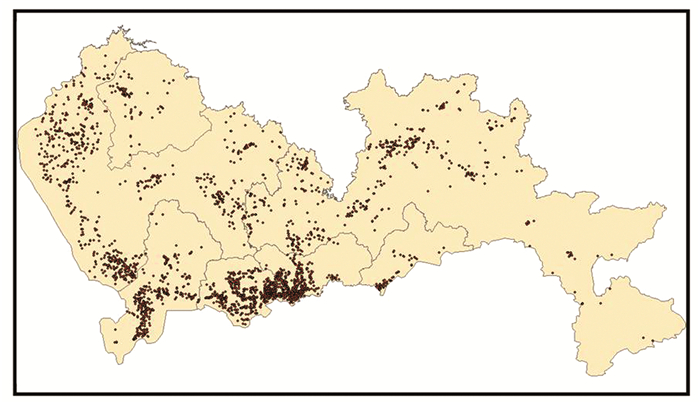
为了进一步探究核密度方法与空间自相关在城市设施热点探测的应用效果,本文以深圳市为研究区域,城市金融设施POI点为分析数据,采用均匀划分的网格作为基础地理单元来进行空间自相关的分析计算。其中金融设施点的数目为7 486,具体包括银行、ATM、保险公司、投资证券公司以及财务咨询公司。图 3是本次实验的区域及城市设施数据的空间分布情况。
|
| 图 3 金融设施分布散点图 Fig. 3 Dot Maps of the Financial Facilities |
本次研究中,格网单元的大小为50 m。在选择衰减阈值过程中,经过多次测试,包括100~900 m区间的多个取值,通过观察不同阈值的密度分布情况,发现100 m、200 m、300 m三个阈值会导致密度分布主要集中在要素点附近的小范围,设施POI分布的整体特征体现不明显,而对于700 m、800 m和900 m的衰减阈值,密度估计的空间分布过于平滑,不能较好表达点分布格局的局部差异。因此,本文主要考虑400~600 m取值区间,最终选择平均值500 m作为理想阈值。Steiner曾利用该阈值作为人们在城市空间中活动的范围界线[22]。由于核密度法已经考虑了空间衰减效应,所以自相关分析选择固定距离范围作为权系数,而在采样法的基础上选择反距离方式计算G*i值。自相关分析的距离阈值均设为500 m。
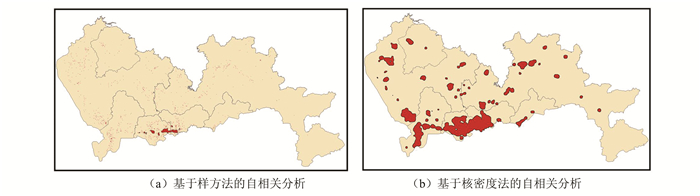
利用Getis-Ord G*i统计方法,可以得到研究区域内设施的局部空间聚集特征,图 4(a)和图 4(b)分别表示基于样方法与基于核密度法的具有显著统计学意义的热点分布图。为了更好地表达热点的空间分布特征,我们将邻接地理单元合并成更大范围的聚类区块。由实验图可知,不管是基于样方法还是基于核密度聚合方法进行自相关分析,深圳的金融设施POI点成显著的空间自相关分布格局,而且金融热点区块集中分布于福田区及其周边区域,说明深圳市各行政区划的经济发展情况有所差异,经济活动布局的区域性较强。另外通过观察发现,样方法的人为划分导致设施空间正相关程度明显弱于核密度方法,热点区块的分布非常零散,小面积区块占据主要的城市空间(图 4(a))。图 4(b)中核密度聚合的热点分布则较集中,区域内出现较多的是大面积的聚类区块类型,具有块状集聚、轴状延伸的格局。具体是以南部中心城区为核心,以西、中、东三条发展轴和南、北两条发展带为基本骨架,形成“三轴两带多中心”的轴带组团结构,与深圳市总体规划(2010~2020年)内容吻合[23]。参考深圳市的各个分区规划,我们可以对图 4的分析结果做进一步的验证:① 首先,从图 4(b)可以发现,在福田区,热点的局部分布范围覆盖了以深南大道为城市发展主轴的市中心区,以及华强北商业中心区域,该结果满足深圳市福田区分区规划(1998~2010年)的要求;② 其次,在罗湖区域,热点以罗湖商贸中心为极核,沿深南大道等交通路线向周围扩展,符合深圳市罗湖区分区规划(1998~2010年);③ 另外,对于南山区的热点分布,我们发现主要以深南大道、滨海大道为主要骨架的东西向扩展轴,以工业大道为骨架的南北向扩展轴,整体上符合深圳市南山区分区规划(1998~2010年)要求的“双十字”型城市空间发展模式[23]。
|
| 图 4 全局范围内金融设施的具有显著统计学意义的热点 Fig. 4 Statistically Significant “Hot Spots” of the Financial Facilities in the Global Region |
在全局范围热点分析的基础上,选择福田区作为局部研究区域(图 5、图 6),核密度计算的衰减阈值降低为300 m,以此突出点分布格局的局部差异。图 5中,样方法支持下的POI分布密度局限于单个网格,核密度估计的结果更好地保持了城市设施服务分布的连续性特征;此外,图 6中,通过对密度属性单元的Getis-Ord G*i测度,核密度支持下的自相关分析可以挖掘出当前局部范围内的热点区域,比较样方法的Getis-Ord G*i分析更符合片区的分区规划[23]。
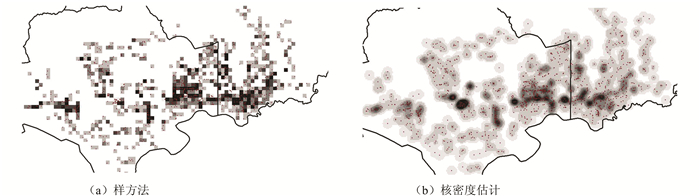
|
| 图 5 利用样方法与核密度方法计算各单元的密度值(衰减阈值为300 m) Fig. 5 Computation of Squares’ Density Value by Using Quadrat Method and Kernel Density Estimation Method |
表 1为图 4中热点分布的相关统计数据,样方法的Getis-Ord G*i分析获得的热点面积虽然小于核密度的自相关分析结果,但是聚类区块个数明显要多于核密度方法。综合以上分析发现,随着属性汇总方式的改变,显著性热点的分析结果也会发生较大的变化,具体表现为空间正相关程度变强、显著性热点面积以及连续性聚类区块增多。考虑到城市基础设施服务影响的空间位置差异,基于核密度方法进行量化热点分析可以更好地获取城市服务分布的连续性、区域性特征。如本次试验中因为金融类服务性质的特殊性,金融基础设施一般集中出现在城市的中心地带,属于服务区域密集型分布,比较图 6中功能分布情况可知,顾及区位影响的聚类结果(图 6(b))可以为城市规划及商业布局提供更为准确的城市经济活动分布信息。
| 热点探测方法 | 显著性网格单元/个 | 显著性热点区块/个 | 热点区块总面积/km2 |
| 样方法与自相关分析融合方法 | 4 871 | 2 066 | 12.177 5 |
| 核密度法与自相关分析融合方法 | 67 637 | 48 | 169.092 5 |
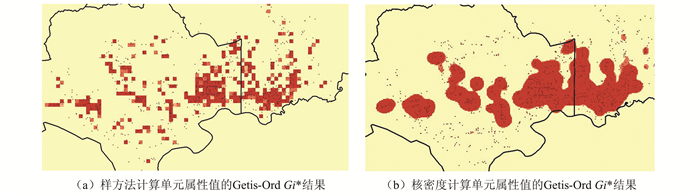
|
| 图 6 局部范围内(福田区)样方法与核密度法支持下的设施POI点自相关分析比较(衰减阈值为300 m) Fig. 6 Spatial Autocorrelation Analysis of Facility POIs by Using Quadrat Method and Kernel Density Estimation Method in a Local Region |
G*i值的计算受权系数的影响较大,表现在权系数的形式及权系数的相关参数。为了便于比较样方法与核密度方法对空间自相关的影响,本文只介绍了固定距离范围和反距离方式,事实上通过对其他权系数的实验发现,本实验的结果在其他条件下也适用。
3 结 语鉴于核密度方法中缺少量化统计指标的评价,本研究提出一种城市设施POI分布热点探测的新方法。主要表现在:采用核密度方法计算空间自相关中地理单元的属性值,顾及了设施服务的区位影响;对城市设施点空间分布中的具有显著统计学意义的热点,建立了定量化的计算模型和表达模型,该方法可以减少对连续性地理现象的人为划分所引起的空间模式变化问题。通过利用核密度理论中的“距离衰减效应”以及空间自相关中的量化分析能力,可以为灾害控制、交通事故分析、商业布局、旅游广告推荐以及城市规划等领域提供更为精确的热点分布信息。
| [1] | Xu Xueqiang, Zhou Yixing, Ning Yuemin. Urban Geography[M]. Beijing:Higher Education Press, 1997(许学强,周一星,宁越敏.城市地理学[M].北京:高等教育出版社,1997) |
| [2] | Wang Jingfeng. Spatial Analysis[M]. Beijing:Science Press, 2006:76-84(王劲峰. 空间分析[M]. 北京:科学出版社, 2006:76-84) |
| [3] | Silverman B W. Dehnad K. Density Estimation for Statistics and Data Analysis[M]. London:Chapman Hall, 1986 |
| [4] | Xie Z, Yan J. Kernel Density Estimation of Traffic Accidents in a Network Space[J]. Computers, Environment and Urban Systems, 2008, 32(5):396-406 |
| [5] | Chen Fei, Du Daosheng. Application of the Integration of Spatial Statistical Analysis with GIS to the Analysis of Regional Economy[J]. Geomatics and Information Science of Wuhan University, 2002, 27(4):391-396(陈斐, 杜道生. 空间统计分析与GIS在区域经济分析中的应用[J]. 武汉大学学报·信息科学版, 2002, 27(4):391-396) |
| [6] | Anselin L. Local Indicators of Spatial Association-LISA[J]. Geographical Analysis, 1995, 27(2):93-115 |
| [7] | Ord J K, Getis A. Local Spatial Autocorrelation Statistics:Distributional Issues and Application[J].Geographical Analysis,1995, 27(4):286-306 |
| [8] | Borruso G. Network Density Estimation:A GIS Approach for Analysing Point Patterns in a Network Space[J]. Transactions in GIS, 2008, 12(3):377-402 |
| [9] | Tobler W. A Computer Movie Simulating Urban Growth in the Detroit Region[J]. Economic Geography, 1970, 46(2):234-240 |
| [10] | Sheather S J, Jones M C. A Reliable Data-based Bandwidth Selection Method for Kernel Density Estimation[J]. Journal of the Royal Statistical Society. Series B (Methodological), 1991:683-690 |
| [11] | Elgammal A, Duraiswami R, Harwood D, et al. Background and Foreground Modeling Using Nonparametric Kernel Density Estimation for Visual Surveillance[J]. Proceedings of the IEEE, 2002, 90(7):1151-1163 |
| [12] | Goodchild M, Haining R, Wise S. Integrating GIS and Spatial Data Analysis:Problems and Possibilities[J]. International Journal of Geographical Information Systems, 1992, 6(5):407-423 |
| [13] | Swift A, Liu L, Uber J. Reducing MAUP Bias of Correlation Statistics Between Water Quality and GI Illness[J]. Computers, Environment and Urban Systems, 2008, 32(2):134-148 |
| [14] | Xu Jianhua, Yue Wenze, Tan Wenqi. A Statistical Study on Spatial Scaling Effects of Urban Landscape Pattern:A Case Study of the Central Area of the External Circle Highway in Shanghai[J]. Acta Geographica Sinica,2004, 59(6):1058-1067(徐建华, 岳文泽, 谈文琦. 城市景观格局尺度效应的空间统计规律——以上海中心城区为例[J]. 地理学报, 2004, 59(6):1058-1067) |
| [15] | Wang Jinfeng, Haining R, Cao Z D. Sample Surveying to Estimate the Mean of a Heterogeneous Surface:Reducing the Error Variance Through Zoning[J]. International Journal of Geographical Information Science, 2010, 24(4):523-543 |
| [16] | Chen Jiangping, Zhang Yao, Yu Yuanjian. Effect of MAUP in Spatial Autocorrelation[J]. Acta Geographica Sinica, 2011, 66(12):1597-1606(陈江平, 张瑶, 余远剑. 空间自相关的可塑性面积单元问题效应[J]. 地理学报, 2011, 66(12):1597-1606) |
| [17] | Cao Zhidong, Wang Jinfeng, Gao Yige, et al. Risk Factors and Autocorrelation Characteristics on Severe Acute Respiratory Syndrome in Guangzhou[J]. Acta Geographica Sinica, 2008, 63(9):981-993(曹志冬, 王劲峰, 高一鸽, 等. 广州SARS流行的空间风险因子与空间相关性特征[J]. 地理学报, 2008, 63(9):981-993) |
| [18] | Chen Peiyang, Zhu Xigang. Regional Inequalities in China at Different Scales[J]. Acta Geographica Sinica, 2012, 67(8):1085-1097(陈培阳, 朱喜钢. 基于不同尺度的中国区域经济差异[J]. 地理学报, 2012, 67(8):1085-1097) |
| [19] | Jiang Haining, Gu Renxu, Li Guangbing. Headquarter Spatial Pattern and Location Choice of Top 500 Enterprises of Chinese Manufacturing Industries[J]. Economic Geography, 2012, 31(10):1666-1673(姜海宁,谷人旭,李广斌. 中国制造业企业500强总部空间格局及区位选择[J]. 经济地理,2012, 31(10):1666-1673) |
| [20] | Hai Beibei, Li Xiaojian, Xu Jiawei. Spatio-temporal Evolution of Rural Settlements in Gongyi[J]. Geographical Research, 2013,32(12):2257-2269(海贝贝,李小建,许家伟. 巩义市农村居民点空间格局演变及其影响因素[J]. 地理研究,2013,32(12):2257-2269) |
| [21] | Ma Xiaodong, Li Quanlin, Shen Yi. Morphological Difference and Regional Types of Rural Settlements in Jiangsu Province[J]. Geographica Sinica, 2012,67(4):516-525(马晓冬,李全林,沈一. 江苏省乡村聚落的形态分异及地域类型[J]. 地理学报,2012,67(4):516-525) |
| [22] | Steiner R L. Traditional Shopping Centers[J]. Access:Research at the University of California Transportation Center,1998, 12:8-13 |
| [23] | Urban Planning Land and Resources Commission of Shenzhen Municipality. The Comprehensive Plan of Shenzhen City (2010-2020)[OL].http://www.szpl.gov.cn/szupb/,2014-07-18(深圳市城市规划委员会. 深圳市城市总体规划(2010-2020)[OL].http://www.szpl.gov.cn/szupb/,2014-07-18) |
 2016, Vol. 41
2016, Vol. 41



