文章信息
- 王沫, 张立华, 于彩霞, 刘涛
- WANG Mo, ZHANG Lihua, YU Caixia, LIU Tao
- 一种基于水深点坡向关系的特征浅点提取方法
- Distilling Feature Shallow Points from Soundings Based on the Slope-Relationship
- 武汉大学学报·信息科学版, 2016, 41(2): 208-213
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 208-213
- http://dx.doi.org/10.13203/j.whugis20140015
-
文章历史
- 收稿日期: 2014-09-09

2. 大连舰艇学院海洋测绘系, 辽宁大连, 116018;
3. 海军出版社, 天津, 300450
2. Department of Hydrography and Cartography, Dalian Naval Academy, Dalian 116018, China;
3. Navy Publishing House, Tianjin 300450, China
数字环境下空间数据的自动制图综合,是现代地图学面临的核心问题之一[1]。许多人认为自动综合是一个具有不良定义性的复杂过程,是地图学与地理信息系统领域的一个重大难题。就数字地图综合过程的实施而言,无论依赖何种概念模式,必须在地物、地貌空间关系分析的层面上设计一定的算法[2]。
海底被水覆盖的不可见性和海图应用要保证航行安全等特殊要求,造成了海图自动制图综合具有更大的复杂性[3, 4]。水深自动综合更是海图综合的难点之一,海图水深点群虽然空间性质相同,但其内部目标之间存在着重要性差异。自从海图进入数字化作业以来,国内外不少学者围绕水深的自动综合也进行了不懈的探索。如文献[5]将水深分为首选水深、背景水深和限定水深,然后将水深按等深线和海岸线进行海底地形分区,不断依首选水深、限定水深、背景水深的顺序进行选取优化;朱颖等则从点群状特征要素的识别与量测入手,根据水深选取的基本原则,探讨基于图形的水深自动综合[6, 7]。目前国内外的水深的自动综合研究中,几乎都强调了找准水深特征浅点的重要性,然而很少有专门的研究,也缺少有效可行的方法。对地图点群自动综合的研究有很多[8, 9, 10, 11, 12, 13],大多在保持空间分布特征的前提下,假定点群目标之间具有等同性进行研究,对点群目标之间的差异性特点关注较少,完全照搬地图点群的综合方法,如果未充分考虑海图水深数据特殊约束条件,则其实际应用价值不大。在当前作业中,水深特征浅点提取很多时候还得依靠人工来完成,不仅效率低,而且提取的质量也依赖于作业员的业务水平和工作态度。
本文利用加权Delaunay三角网和水深数据空间坡向关系,采用定量指标对水深数据进行特征浅点的自动提取,对于提高制图综合的效率和结果的准确性具有理论和现实意义。
1 水深数据的坡向关系及特征浅点 1.1 水深数据的坡向关系描述水深坡向关系是指水深点之间的高低关系的描述,是水深特征浅点提取需要重点考虑的空间关系,主要应分析以下两个方面的因素。
1) 水深坡向关系的参数。 水深数据的深度值,为进行点对间的差值计算提供了数据保证。
2) 点对间的坡向关系描述参数。 水深点间的深度差值,为对点对之间的坡向进行赋值提供了依据。通过差值的“+、0、-”来表示“深、等深、浅”的坡向关系。
1.2 坡向关系的加权处理
构建Delaunay三角网是建立点群空间关系的常用方法之一,它是一系列邻接、不重叠的三角形集合,而且这些三角形的外接圆不包含这个面域的其他任何点。本文在构建水深三角网的基础上,对三角网各边进行加权,即点对之间的“链”进行赋值,通过对“链”的定性描述反映相关的点对之间的坡向关系,为后续的水深特征浅点提取奠定基础。
根据坡向关系中两点水深数值的差值可以用于反映两点坡向关系,可以将两个水深离散点P{Ps,Po}链接得到点对之间的“链”,即L。具体关系如图 1所示。

|
| 图 1 水深点间的坡向关系 Fig. 1 Slope-Relationships Between Soundings |
当d>0时说明Ps高于Po,如图 1(a)所示“链”L的坡向对于Po是“前链”为“+”,对于Ps是“后链”为“-”,且Ps→Po。
当d<0时说明Ps低于Po,如图 1(b)所示“链”L的坡向对于Po是“前链”为“-”,对于Ps是“后链”为“+”,且Po→Ps。
针对本文中进行水深数据之间的坡向关系处理,需要在反映出两点间的深度距离关系的同时,对某一点与所有与其相关的点之间的“链”进行差值排序,这样可以便于分析,得到符合特定空间关系的“链”,进而存储(如表 1)用于下一步计算的内容,为特征线的提取提供依据;同时,将差值的“+”、“0”和“-”赋予每一个指定的“链”,并定义为点对之间的坡向关系描述值。
水深数据的首要作用是保障航行安全,因此,根据水深数据的用途和特点,特征浅点作为最重 要的水深数据,不可轻易进行化简和删除,应优先提取,从而保证海图制图规范的基本要求。如果特征浅点出现丢失,不仅使水深反映的海底地形失真,而且更严重的是为航行安全带来隐患,如图 2所示。
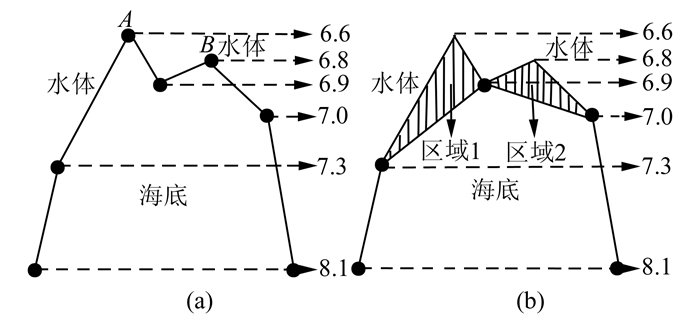
|
| 图 2 海底失真情况 Fig. 2 Distortion of Seabed |
图 2是丢失浅点前后情况的比较,图 2(b)中阴影区域1为丢失最浅点A的海底失真部分,图 2(b)中阴影区域2为丢失相对浅点B的海底失真部分,其结果都会对航行安全造成重大隐患。
在制图综合规范中,水深特征浅点并非一般测绘概念的水深数据点,而是经过综合分析,判定的具有特殊和重要意义的水深点,其提取的准确性直接影响海图质量。制图综合人员通过水深点之间的深度关系来判定水深特征浅点,这种深度关系往往通过水深点之间的坡向关系来描述,因此,坡向关系成为判定水深点之间空间特征性的最直接方法。
在水深综合中,经过实践总结,基于坡向关系判定的特征浅点类型主要有以下两种:
1) 全域的最浅水深点为一级浅点,视为特征浅点;
2) 除全局浅点外,在局部的邻接水深之上的点为相对二级浅点,其为重要的海底地形凸形浅点,也视为特征浅点。
2 水深特征点提取方法 2.1 基于水深差值的坡向特征线提取坡向特征线(以下简称特征线)是用于描述水深点坡向关系树的非一般测绘意义的概念线,是为特征浅点提取提供判定依据的过渡虚拟连线,特征线提取是基于坡向关系提取特征浅点的必要过程。 特征线提取的主要步骤如下。
1) 假设某一类离散水深点集为N,选取N中同一限定条件(条件为设定水深数据的深度值选取阈值区间,即以图上闭合等深区域内的水深数据为一类)下的离散数据所形成的子集 No{Po,…,Pn}∈N,N为非空,区域内特征线起点的不同会影响特征点判定结果,该限定条件的设定,避免区间外数据对在区间内选择数据起点的影响。
2) 搜索No中水深值最小的点(该搜索结果可不唯一,可选取其中任意一个,均视为“特征浅点”)作为提取水深特征线的起始点,即Xo=min{No}。
3) 点Xo∈No{Po,…,Pn}为起始点,计算其与共有三角形中的其它点的水深差值,结果存储于差值集S{R1=X1-Xo,…,Rm=Xm-Xo},m<n,X1,…Xm⊂No;差值点集记录为Pc{P′1{R1},…,P′m{Rm}},选取下一起点为Px=min{Pc}∈No。
4) 以第二个Px为起始点,重复步骤3),出现几种情况的处理方法如下。
(1) 当搜索到的点与起始点的差值为负时,则该起始点被认定为“节点”,搜索结束时,并未将所有点全部连接,则以该“节点”为起始点,再次搜索,以此类推,为了保证不出现数据冗余,每个节点只能搜索两次。
(2) 当搜索到的点与起始点的差值为“0”时,则将起始点直接连接。
(3) 当出现搜索到多个点与起始点的差值为“0”时,则以第一个被搜索的等深点为下一个起始点。
5) 将子集No内的点按照提取顺序重新排列,并以提取的第一个点开始,依次链接点对,直到最后一点为止,所有链接线段的集合为特征线段集,即特征线提取完毕。
在进行特征线提取时,必须满足以下约束条件:① 保证区域内的所有水深点都被特征线连接到;② 保证特征线不会出现闭合现象,避免特征点提取出现问题;③ 为避免分支过多所造成的数据赋值方面的问题,每个节点的分支不多于2个。
2.2 基于特征线坡向的特征点提取在构建Delaunay三角网并提取特征线后,需要利用特征线作为海底地形的骨架线的这一特点,判断线上点对之间坡向特征性,即若要确定特征线上的点是否作为“特征浅点”被提取,其规则是通过记录特征线上点的“前链”、“后链”的赋值关系,认定该点的性质。
本文方法可将水深数据中的最浅点和相对浅点认定为“特征浅点”,应提取;将最深点和相对深点认定为“特征深点”,不作为必要特征点,应视情况提取;其余点认定为“过渡点”和“待定点”,不提取。 提取的基本步骤如下。
1) 将特征线 T{L1,…,Ln,No}中的上的水深点存储于子集No为特征线段子集存储于TL{L1,…,Ln}。
2) “链”L中存储特征线每段的坡向,为了分析方便,以“+、-”进行记录,如果X点到Y的方向值为“+”,则Y的地势低于X,坡向为X→Y,反之为“-”。
3) “特征浅点”的判定
(1) 区域内最浅点认定为“特征浅点”,应提取;
(2) 当非节点的水深点邻接特征线段的坡向关系集中存在为“-,-”的情况时,则说明该点为特征线上的相对浅点,认定为“特征浅点”应提取;
(3) 当节点水深点的分支坡向关系集中存在“-,-”的情况时,认定为“特征浅点”,应提取。
4) 其他情况
(1) 区域内最深点认定为“特征深点”,不提取;
(2) 当非节点的水深点邻接特征线段坡向关系集中存在“+,+”时,则该点认定为 “特征深点”,不提取;
(3) 当节点水深点的分支坡向关系集中存在“+,+”的情况时,认定为“特征深点”,不提取;
(4) 当非节点的水深点邻接特征线段的坡向关系集中存在为 “+,-”时,该点为“过渡点”,不提取;
(5) 坡向关系集中只有前链有赋值时,则该点为“末端点”,不提取;
(6) 若非节点的水深点邻接特征线段存在等深的情况,则该点“前链”与同深度前点的“前链”的赋值相同,该点“后链”与同深度后点的“后链”的赋值相同,其判定方法与(3)中所述方法相同。
3 实例与分析 3.1 水深特征线提取与分析在本实例中,以某一典型开阔区域的水深为实验数据,水深特征线提取实验过程如下。
1) 本实验选取区域内10~20 m区间的水深点作为实验数据,用于Delaunay三角网的构建(如图 3)。

|
| 图 3 三角网构建 Fig. 3 Construction of Triangular Network |
2) 获取区域内最浅水深点Po,以Po为起点,按照水深特征线提取原则,其结果如图 4中实线所示,该过程提取的特征线反映了此区域内海底地形的基本趋势,是水深特征浅点提取中必须要保留的一条虚拟、过渡的海底地形特征线。实验提取的特征线集如表 2所示。
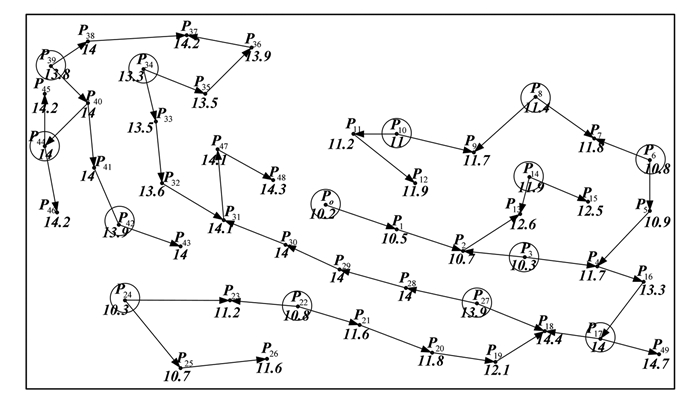
|
| 图 4 特征浅点提取结果 Fig. 4 Results of Distilled Feature Shallow Soundings |
| 特征线 | 点集 | 线段集 |
| L1 | P0,…,P12 | P0P1,…,P11P12 |
| L2 | P2,P13,…,P15 | P2P13,P13P14,P14P15 |
| L3 | P4,P16,…,P26 | P4P16,P16P17,…,P25P26 |
| L4 | P18,P27,…,P43 | P18P27,P27P28,…,P42P43 |
| L5 | P31,P47,P48 | P31P47,P47P48 |
| L6 | P40,P44,P45 | P40P44,P44P45 |
| L7 | P44,P46 | P44P46 |
| L8 | P17,P49 | P17P49 |
1) 对已提取的特征线,按照特征线的连接顺序进行坡向加权赋值,得到点对之间的坡向关系集(如表 3、表 4),从而得到特征线坡向关系如图 4所示的箭头所指方向,方向指向水深相对深点。
| 点 | 前链 | 后链 | 点 | 前链 | 后链 |
| Po | 无 | - | P1 | + | - |
| P3 | - | - | P5 | - | + |
| P6 | - | - | P7 | + | + |
| P8 | - | - | P9 | + | + |
| P10 | - | - | P11 | + | - |
| P14 | - | - | P15 | + | 无 |
| P22 | - | - | P23 | + | + |
| P24 | - | - | P25 | + | - |
| P27 | - | - | P34 | - | - |
| P39 | - | - | P40 | + | + |
| P42 | - | - |
| 点 | 前链 | 后链 | 点 | 前链 | 后链 |
| P2 | + | +,- | P4 | + | +,- |
| P17 | + | -,- | P18 | + | +,+ |
| P44 | 0 | -,- |
2) 根据水深点类型的判定方法可得结果如表 5所示。提取得到“特征浅点”结果如图 4圈定的水深点所示。通过本方法快速提取特征浅点的同时,还可以确定区域内水深点的重要性关系,结果如下:特征浅点为最重要水深点,即首选水深点;特征深点为次级重要水深点,即限定水深点;末段点为待定点;过渡点为背景水深点。该重要性排序结果可以为今后进行结构性水深选取提供次序性依据。
| 类型 | 特征浅点 | 特征深点 | 末端点 | 过渡点 |
| 水
深 点 |
Po、P3、 | P2、P4、 | P12、P15、 | P1、P5、 |
| P6、P8、 | P7、P9、 | P26、P43、 | P11、P16、 | |
| P10、P14、 | P13、P18、 | P45、P46、 | P19、P20、 | |
| P22、P24、 | P23、P31、 | P48、P49 | P21、P25、 | |
| P27、P34、 | P37、P41 | P28、P29、 | ||
| P39、P42、 | P30、P32、 | |||
| P17、P44 | P33、P35、 | |||
| P36、P38、 | ||||
| P40、P47 | ||||
| 数量 | 14 | 10 | 8 | 18 |
将该组实验源数据分别交由4个制图作业人员进行特征浅点提取,人工提取结果与计算机自动提取的特征浅点结果如表 6所示。
| 作业对象 | 错漏/个 | 错误率/% | 用时/min |
| 作业员A | 2 | 14.2 | 8 |
| 作业员B | 3 | 21.4 | 7 |
| 作业员C | 1 | 7.14 | 10 |
| 作业员D | 0 | 0 | 16 |
| 自动提取 | 0 | 0 | 1 |
从表 6可以看出,作业员A、作业员B、作业员C都存在丢失重要的特征浅点的情况,对航行安全影响较大;作业员D虽无错漏,但用时较长。计算机自动提取方法用时明显缩短,并且无“特征浅点”丢失。从对比结果可以得出,本文提出的方法在效率及正确率上都有明显提高。
4 结 语1) 通过理论分析和实验结果验证,该方法可以较好提取“特征浅点”,避免水深综合中漏浅和丢失相对浅点的可能情况的发生。
2) 通过比对实验可知,本文方法与传统作业人员手工作业相比,效率明显提高。
3) 在数字海图制图生产过程中,本方法可以起到对水深数据综合处理结果的质量控制作用,并且可为检查浅点是否错漏提供依据。另外,在提取特征浅点的同时,将实验区域内的水深点群的重要性关系一并确定,可以为今后水深结构性选取研究提供参考依据。
当然,本文选定的实验数据是典型的开阔海域,本方法缺少对多种空间分布类型海区的水深综合结果的比对分析,还需要进一步的研究。另外,No子集的选取影响坡向特征线提取的起点,而起点的不同是否会对特征点提取的结果造成一定的影响,还需深入研究。
| [1] | Wang Jiayao. The Progress and Trend of Automatic Generalization of Spatial Data[J]. Journal of Geomatics Science and Technology,2008,25(1):1-12(王家耀.空间数据自动综合研究进展及趋势分析[J].测绘科学技术学报,2008,25(1):1-12) |
| [2] | Wang Jiayao,Li Zhilin,Wu Fang.Advances in Digital Map Generalization[M]. Beijing:Science Press,2011(王家耀,李志林,武芳.数字地图综合进展[M].北京:科学出版社,2011) |
| [3] | Du Jinghai. The Chart Designing[M]. Beijing:Surveying and Mapping Press,1994(杜景海.海图编辑设计[M].北京:测绘出版社,1994) |
| [4] | Xu Haitao. Research on Automatic Generalization of Sounding Annotation[J]. Hydrographic Surveying and Charting,1997,1(1):19-23(许海涛.海图水深注记自动综合研究[J].海洋测绘,1997,1(1):19-23) |
| [5] | Zoraster Steven, Bayer Steven. Automated Cartographic Sounding Selection[J]. International Hydrographic Review,Monaco,1992,3:103-116 |
| [6] | Zhu Ying,Lu Yi, Jiang Hongyan, et al. Research on Automatic Generalization of Digital Sounding[J]. Hydrographic Surveying and Charting,2009,29(3):48-51(朱颖,陆毅, 蒋红燕, 等.数字海图水深的自动综合探讨[J].海洋测绘,2008,28(2):48-51) |
| [7] | Li Zhiwei,Zhu Ying,Lu Yi, et al. The Identification and Measurement of the Points Form Characteristic on Chart[J]. Hydrographic Surveying and Charting,2009,29(3):16-18(李志炜,朱颖,陆毅,等.海图上点群状特征的识别与量测[J].海洋测绘,2009,29(3):16-18) |
| [8] | Wu Hehai. Principle of Convex Hull and Its Applications in Generalization of Grouped Point Objects[J].Engineering of Surveying and Mapping,1997,6(1):1-6(毋河海.凸壳原理在点群综合中的应用[J].测绘工程,1997,6(1):1-6) |
| [9] | Ai Tinghua, Liu Yaolin. A Method of Point Cluster Simplification with Spatial Distribution Properties Preserved[J]. Acta Geodaetica et Cartographica Sinica,2002,31(2):175-180(艾廷华,刘耀林.保持空间分布特征的点群化简方法[J].测绘学报,2002,31(2):175-180) |
| [10] | Sester M.Optimization Approaches for Generalization and Data Abstraction[J]. International Journal of Geographical Information Science, 2005, 19(8/9):871-897 |
| [11] | Yan Haowen,Wang Jiayao. A Generic Algorithm for Point Cluster Generalization Based on Voronoi Diagrams[J]. Journal of Image and Graphics,2005,10(5):633-636(闫浩文,王家耀.基于Voronoi图的点群目标普适综合算法[J].中国图像图形学报,2005,10(5):633-636) |
| [12] | Cai Yongxiang,Guo Qingsheng. Points Group Generalization Based on Konhonen Net[J]. Geomatics and Information Science of Wuhan University,2007,32(7):626-629(蔡永香,郭庆胜.基于Kohonen网络的点群综合研究[J].武汉大学学报·信息科学版,2007,32(7):626-629) |
| [13] | Wang Jiayao,Qian Haizhong. Cartographic-generalization-knowledge and Its Application[J]. Geomatics and Information Science of Wuhan University,2006,31(5):382-386(王家耀,钱海忠.制图综合知识及其应用[J].武汉大学学报·信息科学版,2006,31(5):382-386) |
 2016, Vol. 41
2016, Vol. 41


