文章信息
- 吴辉, 刘永波, 秦承志, 刘军志, 江净超, 朱阿兴
- WU Hui, LIU Yongbo, QIN Chengzhi, LIU Junzhi, JIANG Jingchao, ZHU A-Xing
- 流域最佳管理措施情景优化算法的并行化
- Parallelization of an Optimization Algorithm for Beneficial Watershed Management Practices
- 武汉大学学报·信息科学版, 2016, 41(2): 202-207
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 202-207
- http://dx.doi.org/10.13203/j.whugis20140048
-
文章历史
- 收稿日期: 2014-02-20

2. 中国科学院大学, 北京, 100049;
3. 加拿大圭尔夫大学地理系, 圭尔夫, N1G 2W1;
4. 南京师范大学地理科学学院, 江苏南京, 210097;
5. 美国威斯康星大学麦迪逊分校地理系, 麦迪逊, 53706
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Department of Geography, University of Guelph, Guelph, Ontario N1G 2W1, Canada;
4. Nanjing Normal University, Nanjing 210097, China;
5. Department of Geography, University of Wisconsin-Madison, Madison WI 53706, USA
最佳管理措施(beneficial management practices,BMPs)是为了控制和削减农业非点源污染、保护土壤资源、改善水质及流域生态环境而在流域单元内采取的一系列措施[1, 2, 3]。BMPs在流域空间上的选择、配置问题是一个高度复杂的非线性问题:一方面,BMPs在不同空间单元上配置所产生的环境效益不同;另一方面,BMPs的实施和管理需要考虑其经济效益,如建设费、管理费等经济成本。因此,如何在流域尺度下选择和优化配置BMPs是当前研究的热点。
最佳管理措施空间配置情景优化(简称BMPs情景优化)所采用的优化算法通常为遗传算法:首先,算法随机生成种群(即一定数量的BMPs空间配置情景);之后,为个体适应度计算阶段,即调用流域模型(如SWAT模型)和需要考虑的其他因素的模型(如进行成本计算的经济模型)对每个情景进行评价,根据评价结果,计算种群个体的适应度;然后,进行遗传、变异产生新的种群,如此逐代进化,种群中适应度较高的个体被保留下来,从而获得最优的BMPs配置方案[4]。由于BMPs情景优化算法需要结合流域模型进行大量的迭代运算,因此,利用优化算法搜索最优措施空间配置方案需要花费大量时间[5]。尤其是当分布式流域模型模拟的时空尺度日益精细化,模拟的流域面积增大,BMPs种类增多,模拟时间范围不断变长,BMPs情景优化需要大量的计算时间。传统的串行计算无法解决这一难题。
并行计算是解决这种复杂地理计算耗时过长问题的有效途径,已在地学计算的诸多领域中得到了有效应用[6, 7, 8]。但目前国内外对于BMPs情景优化并行化的研究较缺乏。Maringanti等[9]应用SWAT模型和非支配排序遗传算法(NSGA-II),在流域面积为1 956 km2的Wildcat Creek 流域进行了BMPs的空间优化,研究表明利用高性能集群的4个计算节点(32个处理器)进行并行化后,计算时间显著减少。但是,文献[9]并没有对BMPs情景优化算法(NSGA-II)的并行化方法进行介绍和说明,此外,有研究表明,ε-NSGA-II算法(Epsilon non-dominated sorted genetic algorithm)在优化效率、稳定性和易用性等方面要高于NSGA-II算法[10, 11],而且ε-NSGA-II算法的并行化尚未见报道。
本文在对BMPs情景优化ε-NSGA-II算法进行可并行性分析的基础上,采用主从式并行策略对算法中占计算量主体部分的个体适应度计算步骤进行了并行化设计,并基于消息传递接口(MPI)并行编程库实现了BMPs情景优化算法的并行化。
1 BMPs情景优化ε-NSGA-II算法BMPs情景优化ε-NSGA-II算法源于NSGA-II算法,NSGA-II算法是由非支配排序遗传算法(Non-dominated Sorted Genetic Algorithm,NSGA)改进后的遗传算法。NSGA-II算法在NSGA算法的基础上采用了精英保留策略,能防止优解的丢失,提高了算法的收敛精度和速度,同时加入了拥挤度距离计算,确保精英集中的非支配解的多样性。ε-NSGA-II算法是在NSGA-II算法基础上进行改进,加入了ε支配调整策略,能够保持最优解集的合理分布,同时能够自动调整算法的参数及终止条件,进一步提高了算法的优化效率[12]。
进行BMPs情景优化时,ε-NSGA-II串行算法流程如下:
步骤1:以随机方法初始化种群,产生一定数量的BMPs情景。
步骤2:多目标评价(个体适应度计算),即调用流域模型和经济模型对每个BMPs情景的多个目标(如减沙率最大、成本最小)进行计算。
步骤3:根据个体适应度计算结果,对种群中的所有个体进行非支配排序[12],排序得到的非支配解保留到一个集合中(称为精英集)。
步骤4:判断是否达到算法的终止条件(如最大进化代数),如果没有达到终止条件,则对种群进行交叉、变异操作,产生新的种群,转到步骤2。如果达到了终止条件,则算法停止执行,最终获得的精英集为Pareto最优集或近似最优集。
根据ε-NSGA-II算法流程以及BMPs情景优化过程中各步骤的计算特点,该算法的可并行性分析如下:
1) 种群初始化时,算法通过调用随机函数产生一定数量的BMPs情景,该过程具有可并行性,但其计算量相对较小(串行算法实测时该步骤约占总运行时间的1%),考虑到并行时增加的通信开销,因此不需要并行。
2) 对种群中所有BMPs情景的环境效益计算时,需要反复迭代运行全分布式流域模型,因此该步骤具有较高的计算密集性,较耗时(实测约占串行算法总运行时间的94%),由于每个情景的效益评价是相互独立的,因此该步骤具有可并行性,通过并行化有可能缩短计算时间。
3) “非支配排序”、“选择”和“交叉”计算步骤需要不同个体的交互操作,因此个体间具有依赖性,可并行性较低(实测约占串行算法总运行时间的4%);而变异操作虽然具有可并行性,但计算量相对较小(实测约占串行算法总运行时间的1%),不需要并行。
2 BMPs情景优化并行算法设计与ε-NSGA-II算法实现采用主从式并行策略对遗传算法进行并行化设计,以利用并行集群设备的多节点计算能力来提高ε-NSGA-II算法的计算速度。主从式并行的遗传算法由主节点(管理节点)存储种群,进行选择、交叉、变异等遗传操作,从节点(计算节点)计算适应度。与其他并行化方式相比,主从式并行方式不改变传统串行遗传算法的工作方式,尤其适合于适应度评价计算量大的BMPs情景优化问题。
基于主从式并行策略可对ε-NSGA-II算法进行并行算法设计,假设种群规模为n,有p(p<n)个计算节点可供使用(当p≥n时,说明有足够多的计算资源,则不需要考虑负载均衡调度,这种情况实际中较少出现,本研究考虑了更通用的p<n的情况),采用消息传递方式实现主进程与从进程之间的通信,并行算法具体步骤如下:
步骤1:管理节点初始化第一代父代种群P0,共n个染色体(每个染色体表示一个BMP情景)。
步骤2:管理节点从当前种群中取出p个染色体分发到p个计算节点上进行多目标评价,评价结果由计算节点通过消息传递发送回管理节点。
步骤3:管理节点接收所有计算节点发回的评价结果后,从当前种群剩余的染色体中再取出p个,转到步骤2继续分发计算任务和接收计算结果,直到剩余的染色体全部计算完,进入步骤4。
步骤4:由管理节点对接收到的n个BMPs情景评价结果进行非支配排序,将非支配解保留到精英集中,并判断是否到达终止条件(如最大进化代数),如果是,则算法结束;否则对种群中的个体进行遗传操作(交叉和变异),产生新的种群,转到步骤2进行多目标评价。
本文基于消息传递接口(MPI)[13] 编程库实现了主从式并行ε-NSGA-II算法,以利用并行集群设备的多节点计算能力。算法的C++伪代码如图 1所示。

|
| 图 1 BMPs情景优化并行化算法的C++伪代码 Fig. 1 The C++ Pseudo Code of Parallel Algorithm for BMPs-Optimization |
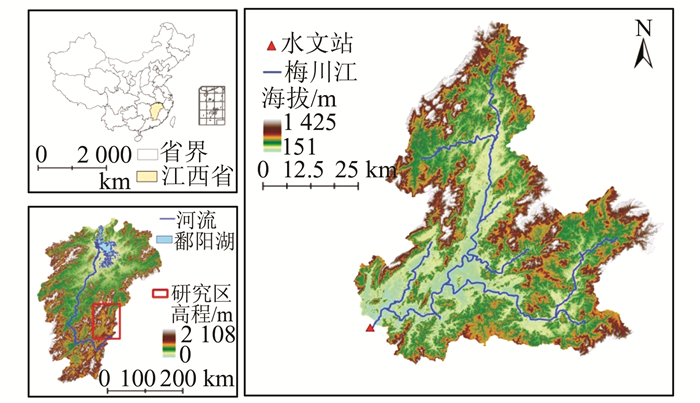
研究区选取了江西省赣江上游的梅川江流域(见图 2),海拔高度151~1 425 m,面积为6 366 km2,属于大型流域。梅川江流域为亚热带湿润气候,年平均温度17℃,平均降水量1 706 mm。由于山地面积大、坡度陡、土层薄、降雨量大等原因,该流域水土流失严重,生态环境脆弱,受气候变化和人类活动影响非常显著,开展管理措施空间配置优化十分必要。
研究选择了退耕还林、免耕和梯田三种管理措施,在研究区内370个农地地块上,以最大化流域侵蚀削减率和最小化费用为目标进行BMPs情景优化。所利用的数据包括流域模拟所需要的DEM、土地利用、土壤类型等空间数据和降雨、温度、风速、太阳辐射等气象数据,以及BMPs成本计算所需要的数据。
|
| 图 2 梅川江流域位置示意图 Fig. 2 Location of Meichuanjiang Watershed |
流域模型是用来评估BMPs实施对流域水文和侵蚀等过程的影响。在BMPs情景优化中,流域模型在空间上需是全分布式,才能精细刻画不同空间配置的管理措施对流域过程的影响。本研究中BMPs评价选择了一个全分布式流域模型SEIM(spatially explicit integrated modeling)[14]。它是一个模块化的流域模型,可以模拟水文、侵蚀和生态等过程,并可以根据研究目的选择每个子过程的算法及其对应的模块。模型模拟采用的空间分辨率为180 m,模拟时段从2009年1月1日~2010年12月31日,时间步长为1天,模型流量模拟的纳什系数达到0.81,泥沙模拟的纳什系数为0.63,说明流量和泥沙模拟精度已达到接受范围。
BMPs情景的泥沙削减率计算是通过与一个基准情景(baseline scenario),即当前未实施BMPs时的侵蚀评价结果,做差值计算,具体计算公式如下:
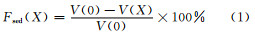
式中,Fsed(X)表示BMPs实施后的泥沙减少率(%);V(0)是基准情景下侵蚀所产生的泥沙模拟量(吨);V(X)是某个BMPs情景下侵蚀所产生的泥沙模拟量(吨)。
在BMPs情景优化中,经济模型也十分重要,这是由于实际的管理措施不能不考虑经济成本因素。本研究以BMPs成本计算组件[15]作为经济模型,来评价优化过程中每个BMPs方案的成本。BMPs方案的成本越小,说明经济效益越高,其计算公式如下:
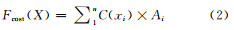
式中,Fcost(X)是该BMPs情景的成本费用(元);C(xi)表示在第i个地块上单位面积BMPs实施费用(元/公顷);Ai表示第i个地块的面积;BMPs费用数据由通过野外调查或者查阅相关文献获得。
3.3 测试环境和参数为了验证本文实现的BMPs情景优化并行算法的效率,选择一个IBM刀片集群平台对算法进行测试。该集群包括1个管理节点和134个计算节点,管理节点配置有2路Intel Xeon E5650的2.66 GHz 6核处理器,24 GB的DDRIII内存;每个计算节点配置2路Intel Xeon E5650的2.0 GHz 6核处理器(共12核),内存是24 GB的DDRIII。节点之间的网络是千兆局域网络,可提供1 GB/s的IO带宽。软件环境为RedHat Enterprise Linux Server操作系统,gcc 4.1.2 编译器和Open MPI 1.3.3并行编程库。
算法测试使用到52个计算节点,每个节点最多用10个核,剩余2个核留给本机系统程序的运行,以避免测试的并行算法与本机系统程序抢夺计算资源而影响测试时间。ε-NSGA-II并行算法在测试时所设参数如下:种群规模为512,最大进化代数为100,交叉概率为0.5,变异概率为0.1。
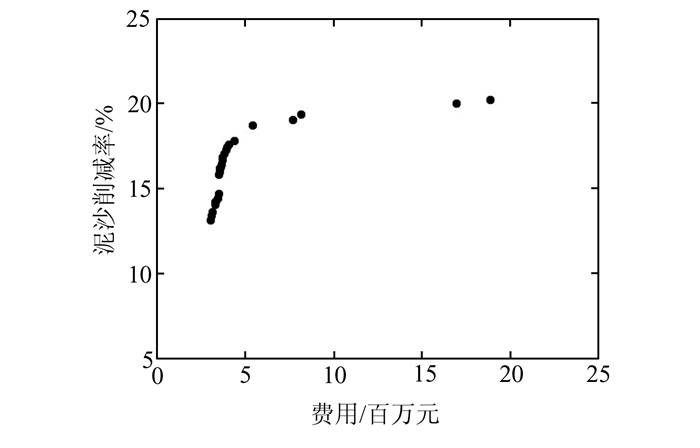
3.4 实验结果经ε-NSGA-II并行算法优化后,研究区获得26个最优BMPs配置方案,其泥沙削减率和费用关系如图 3所示,泥沙的削减率约为13.2%~ 20.2%,需要相应投入的管理措施费用为3.6~18.9百万元。
|
| 图 3 最优方案的泥沙削减和费用关系图 Fig. 3 Pareto Optimal Solution of BMPs |
得到上述结果的优化过程计算量非常大,如图 4所示,核数为128、256和512时所测试的时间是实际运行了100代的时间,均以天计。串行算法和核数较少(8、16、32、64)时并行算法的运算时间更加漫长,因此本文用运行2代的计算时间(t2)推算运行100代的大致时间(t100=t2×50)。为了验证该推算方法的可信性,将核数为128、256和512时所运行2代的实测时间分别乘以50,推算运行100代的大致时间,经与对应的实测100代的运行时间对比,相对误差分别为0.30%、-1.02%和1.13%,这说明以并行算法运行2代的实测时间推算得出运行100代的大致计算时间是可信的。并行算法在不同核数下所测试的运行时间(图 4)表明,当并行算法利用512个核计算时,计算时间显著减少,从串行计算时估计为近1年的时间缩短到1天。
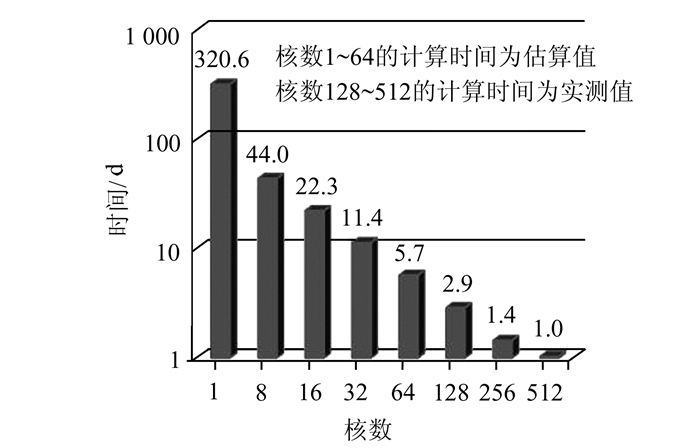
|
| 图 4 情景优化算法在不同核数下运行100代所需的时间 Fig. 4 Computation Time of Parallel BMPs-Optimization Algorithm with 100-Generation Optimization on Different Numbers of Cores |
情景优化并行算法的加速比曲线(图 5)表明,当核数从8变化到512时,算法加速比呈递增趋势,当核数为512时加速比最大,达到310,当核数在8~256范围时接近线性加速比。情景优化并行算法的并行效率曲线如图 6所示,随着核数的增加,通信开销也增大,并行效率从0.91(8核时)逐渐下降,但最低也达到0.61(512核时)。

|
| 图 5 情景优化并行算法加速比 Fig. 5 Speedup Ratio of Parallel BMPs-Optimization Algorithm |
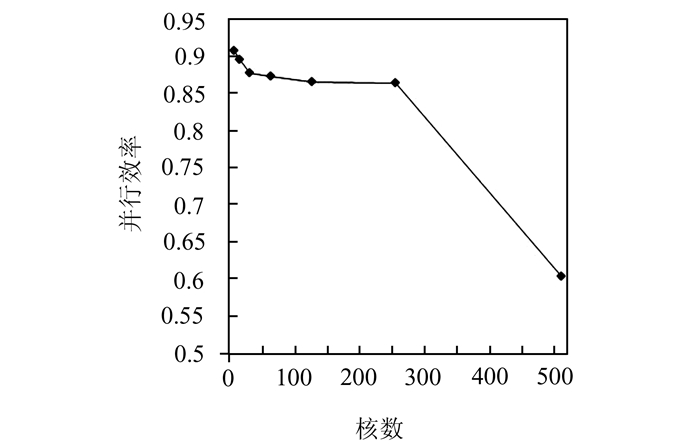
|
| 图 6 情景优化并行算法并行效率 Fig. 6 Parallel Efficiency of Parallel BMPs-Optimization Algorithm |
本文研究了如何利用并行计算来提高流域最佳管理措施情景优化的效率,在BMPs优化算法(ε-NSGA-II)可并行性分析的基础上,采用主从式并行策略,利用MPI消息传递并行编程模型对ε-NSGA-II算法进行了并行化。在一个IBM刀片集群平台上的测试结果表明,本文设计实现的BMPs情景优化并行算法具有很好的并行性能,在大流域应用的并行效率较高:当核数从8到256变化时,几乎接近线性加速比,当核数为512时,加速比达310倍。算法并行效率最高为0.91,最低也达到了0.61。
| [1] | Logan T J. Agricultural Best Management Practices for Water-Pollution Control-Current issues[J]. Agriculture Ecosystems & Environment, 1993, 46(1-4):223-321 |
| [2] | Ripa M, Leone A, Garnier M, et al. Agricultural Land Use and Best Management Practices to Control nonpoint Water Pollution[J]. Environmental Management, 2006, 38(2):253-266 |
| [3] | Rao N S, Easton Z M, Schneiderman E M, et al. Modeling Watershed-scale Effectiveness of Agricultural Best Management Practices to Reduce Phosphorus Loading[J]. Journal of Environmental Management, 2009, 90(3):1385-1395 |
| [4] | Arabi M, Govindaraju R S, Hantush M M. Cost-effective Allocation of Watershed Management Practices Using a Genetic Algorithm[J]. Water Resources Research, 2006, 42(10):W10429-1-14 |
| [5] | Gitau M W, Chiang L C, Sayeed M, et al. Watershed Modeling Using Large-Scale Distributed Computing in Condor and the Soil and Water Assessment Tool model[J]. SIMULATION, 2012, 88(3):365-380 |
| [6] | Rouholahnejad E, Abbaspour K C, Vejdani M, et al. A Parallelization Framework for Calibration of Hydrological Models[J]. Environmental Modelling & Software, 2012, 31(5):28-36 |
| [7] | Li Jian, Li Deren, Shao Zhenfeng. A Streaming Data Delaunay Triangulation Algorithm Based on Parallel Computing[J]. Geomatics and Information Science of Wuhan University, 2013, 38(7):794-798(李坚, 李德仁, 邵振峰. 一种并行计算的流数据Delaunay构网算法[J]. 武汉大学学报·信息科学版, 2013, 38(7):794-798) |
| [8] | Qi Kunlun, Chen Yumin, Wu Huayi, et al. Parallel processing in Eigenfunction-based Spatial Filtering Using MPI+OpenMP Hybrid Parallelization[J]. Geomatics and Information Science of Wuhan University, 2013, 38(6):742-750(祁昆仑, 陈玉敏, 吴华意, 等. MPI+OpenMP环境下的特征函数空间滤值并行化方法研究[J]. 武汉大学学报·信息科学版, 2013, 38(6):742-750) |
| [9] | Maringanti C, Chaubey I. High Performance Computing Application to Address Non-point Source Pollution at a Watershed Level[C]. American Society of Agricultural and Biological Engineers Annual International Meeting. Reno, NV, 2009 |
| [10] | Kollat J B, Reed P M. The Value of Online Adaptive Search:A Performance Comparison of NSGAⅡ, ε-NSGAⅡ and εMOEA[C]. Third International Conference, EMO 2005, Guanajuato, Mexico, 2005 |
| [11] | Kollat J B, Reed P M. Comparing State-of-the-Art Evolutionary Multi-objective Algorithms for Long-term Groundwater Monitoring Design[J]. Advances in Water Resources, 2006, 29(6):792-807 |
| [12] | Devireddy V, Reed P. Efficient and Reliable Evolutionary Multiobjective Optimization Using ε-dominance Archiving and Adaptive Population Sizing[C]. Genetic and Evolutionary Computation Genetic and Evolutionary Computation Conference, Seattle, WA, USA, 2004 |
| [13] | Gropp W, Lusk E, Doss N, et al. A High-performance, Portable Implementation of the MPI Message Passing Interface Standard[J]. Parallel Computing, 1996, 22(6):789-828 |
| [14] | Liu J, Zhu A, Liu Y, et al. A Layered Approach to Parallel Computing for Spatially Distributed Hydrological Modeling[J]. Environmental Modelling & Software, 2014, 51(1):221-227 |
| [15] | Chaubey I, Maringanti C, Popp J. Development of a Multiobjective Optimization Tool for the Selection and Placement of Best Management Practices for Nonpoint Source Pollution Control[J]. Water Resources Research, 2009, 45(6):W06406-1-15 |
 2016, Vol. 41
2016, Vol. 41



