文章信息
- 倪皓晨, 伍钟洁, 郏建, 徐地保, 芮一康, 王结臣
- NI Haochen, WU Zhongjie, JIA Jian, XU Dibao, RUI Yikang, WANG Jiechen
- 一种基于Delaunay三角网的栅格线划矢量化方法
- A Gird Line Vectorization Method Based on Delaunay Triangulation
- 武汉大学学报·信息科学版, 2016, 41(2): 184-189
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 184-189
- http://dx.doi.org/10.13203/j.whugis20140100
-
文章历史
- 收稿日期: 2014-10-09

2. 南京大学地理信息科学系, 江苏南京, 210023;
3. 天津市测绘院, 天津, 300381;
4. 江苏省测绘工程院, 江苏南京, 210013
2. Jiangsu Province Surveying and Mapping Engineering Institute, Nanjing 210013, China;
3. Department of Geographic Information Science, Nanjing University, Nanjing 210023, China;
4. Tianjin Institute of Surveying and Mapping, Tianjin 300381, China
扫描地图矢量化通常指对纸质地图进行扫描数字化、图像增强、地图分色、要素识别、栅格跟踪等一系列处理过程,其本质是将用点阵阵列表示的地图要素转化为二维平面的坐标对,并重构要素间的拓扑关系[1]。在栅格地图中,地图要素的表达方式主要有点、线、面三种,一个地图要素实体往往由多个栅格单元组成,而各地图要素的中心点(线)位置(矢量化后的坐标点),通常不能直接从栅格地图上直接获取。点要素形状简单,可以通过坐标空间加权的方式,获取其中心点坐标;线要素栅格点呈空间分布,不能通过简单的空间统计方式获取其中心线坐标;面要素由闭合的栅格线表征其空间属性。如何快速准确地提取栅格线划的中心线(骨架线),成为栅格地图矢量化研究的热点及难点。
地图矢量化方法目前已有较多研究成果。上世纪90年代初期,已有学者设计了基于计算视觉的灰度单色地图矢量化系统,初步实现了从地图扫描、对象识别、线划跟踪以及图形数据自组织[2]。随着信息技术、人工智能技术的不断发展,一些学者也开展了在复杂彩色背景下的地图矢量化方法研究,力图实现全要素地图的矢量化操作[3]。通过对现有线状要素矢量化方法对比分析,线状要素矢量化算法按其算法设计思路可以归为两类,即迭代算法与非迭代算法[4]。迭代算法是反复执行某一操作,直到生成线划要素矢量线为止。这类算法通常能较好地保持原图的细节,保持线段的连续性,但往往需要多次迭代,有较高的时间复杂度,对噪声敏感,如经典细化算法[5]、蚁群算法[6]、神经网络算法[7]等。非迭代矢量化算法主要指不使用轮廓像素剔除,而采用辅助技术手段直接提取骨架线。非迭代算法设计思路很多,主要有基于图像域与轮廓几何分析的矢量化方法,如基于主曲线的提取算法[8]、经典轮廓匹配算法[9]等;基于栅格点跟踪的矢量化方法,如基于多重判据的自动跟踪算法[10]、基于滑动窗口分割及序贯跟踪的矢量化方法[3]等;基于图形边缘空间拓扑分析的矢量化方法,如基于Voronoi图的扫描地图矢量化方法[11]等。
迭代与非迭代算法,虽然在算法设计思路上有区别,但大部分都是基于对图像栅格单元空间邻域分析或图形域几何分析实现要素矢量化的,只有少数研究采用空间拓扑分析的方法进行要素矢量化操作[11]。Delaunay三角网作为Voronoi的空间对偶图,是一种常用的空间剖分方法。目前,有学者利用Delaunay三角网实现了街道数据中轴线提取[12]、多边形骨架线提[13]取及空间场数据的骨架化操作[14]。上述中,其研究对象虽然皆是矢量图形,但其骨架线的提取思想恰好满足栅格线划矢量化的需求。本文根据栅格图像的特点,提出一种基于Delaunay三角网的栅格地图矢量化方法,运用Delaunay三角网对栅格线划进行空间剖分,根据单个Delaunay三角形的形状特征,提取线划要素骨架线,实现栅格线划矢量化。
1 基本思想与技术流程Delaunay三角网是一种在数值分析、图像处理等领域常用的空间剖分方法[15]。Delaunay三角网以空间离散点为基准,把整个空间剖分为最接近于规则化且唯一的三角形集合。以线划要素边缘栅格点生成的Delaunay三角网,在边缘轮廓平滑的直线与曲线区段中,相邻的Delaunay三角形,在形状上十分相似:一边较短(一个像元宽),另两边较宽(基本等同于线划要素宽度),可近似拼接为矩形或平行四边形的三角网,如图 1所示。Delaunay三角网沿要素边缘方向,对线划要素进行了空间剖分。这种剖分就如同用微分扇形对圆进行剖分,改变了原始图形的细部结构,使其便于量测。这种形状规则对称,单体三角形沿线划要素横向展开、整个三角网沿线划要素纵向展开的Delaunay三角网,可大体表征线划要素的结构与走向,使线划要素转变为一个个微分矩形或四边形。经此变换,就可以通过量测这些微分单元,获得线划要素内部几何特征,进而提取线划要素骨架线。
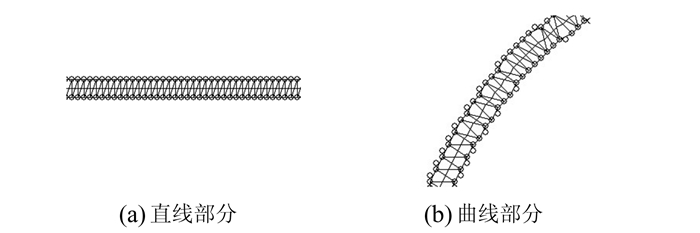
|
| 图 1 线划要素三角网剖分 Fig. 1 Triangle Network Subdivision of Line Element |
基于上述思想,本文提出一种基于Delaunay三角网的栅格线划矢量化方法,主要流程如下。
1) 栅格地图预处理:对原始栅格图像进行图像预处理、图像增强等操作,然后进行图像二值化。如果待矢量化地图为彩色地图,则先进行分色处理,得到不同要素的单色栅格图。
2) 线划要素实体识别:对图像进行基于像元八邻域标记的栅格线划要素识别[16],提取图像中相互独立的线划要素实体。
3) 边缘点集生成:对已提取识别的线划实体,进行数学形态学边缘提取[17],获得边缘栅格,进而转化为各个线划对象的边缘点集。
4) Delaunay三角网生成:采用较成熟的扫描线Delaunay三角网生成算法[18],对所有线划实体的边缘点集逐一生成Delaunay三角网。
5) 线划要素骨架线提取:根据Delaunay三角网中三角形间的拓扑关系,利用基于Delaunay三角形中位线跟踪的线划要素骨架线提取方法,提取线划要素骨架线。
本方法的核心是基于Delaunay三角形公共边中点追踪的线划要素骨架线提取,下面详细论述。
2 基于Delaunay三角形公共边中点追踪的线划要素骨架线提取本文所述的骨架线提取方法分为两个处理步骤,即剔除干扰三角形和骨架线跟踪。
2.1 剔除干扰三角形由于Delaunay三角剖分是在空间散布的离散点上进行,最终形成的三角网一定会有凸包,以满足Delaunay规则[19]。因此,在图 2中可以看到,如果要素自身弧度很大或呈近圆形,三角网不只会出现在线划要素轮廓范围内。为了确保骨架线跟踪的准确性,首先要剔除这些不在轮廓线范围内的三角形。
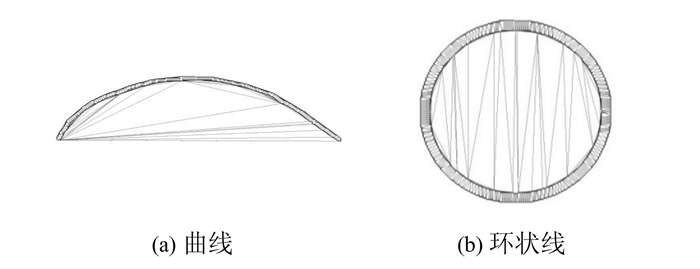
|
| 图 2 原始三角网 Fig. 2 Original Triangle Net |
经反复试验与观察,需剔除的干扰三角形主要有两类:一类位于线划要素轮廓范围外,另一类位于线划要素边缘轮廓上,如图 3所示。为了实现剔除干扰三角形,需获取每个三角形内心位置的连通标识值和边缘矩阵标识值:若连通标识值与该线划要素连通标识值不同,则表明此三角形位于线划轮廓范围外;若边缘矩阵标识值与该线划要素边缘矩阵标识值相同,则表示此三角形位于线划要素边缘轮廓上。图 3、图 4别显示了剔除操作前后的三角网展开情况。在图 3中圆圈表示线划要素边缘点集,粗线表征线划要素轮廓范围。在粗线范围外的三角形为干扰三角形,需剔除。

|
| 图 3 原始的三角网 Fig. 3 Original Triangle Net |
|
| 图 4 删除前的三角网 Fig. 4 Processed Triangle Net |
在剔除干扰三角形后,线划要素边缘点集三角网形成一个沿线划延伸方向展开、一一相连的三角形序列,如图 1所示。借助Delaunay三角型的形态特征及三角形间的拓扑关系,以追踪相邻三角形公共边中点的方式,实现线划要素骨架线的提取。具体算法流程如图 5。
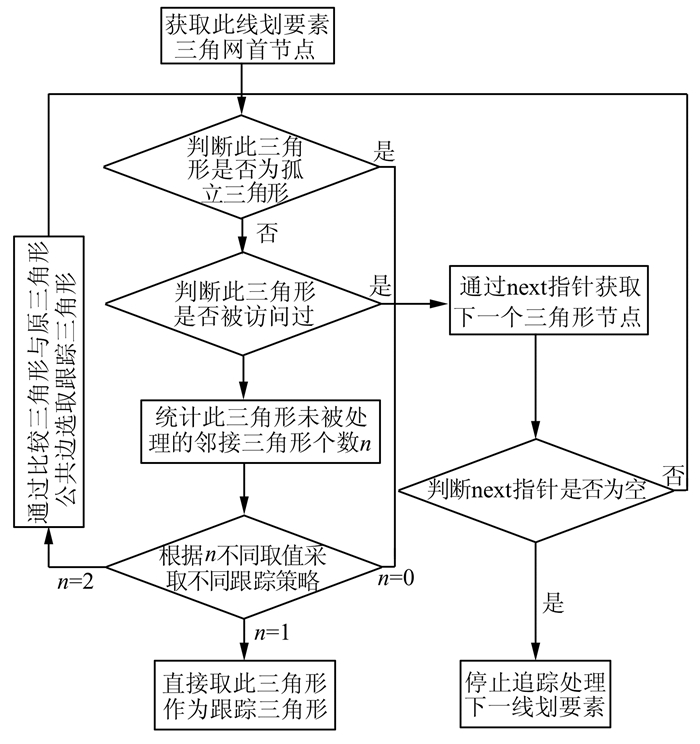
|
| 图 5 骨架线跟踪流程图 Fig. 5 Flowchart of Skeleton Line Trace |
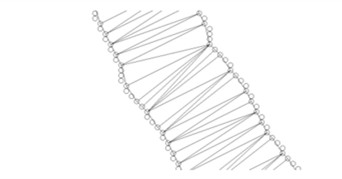
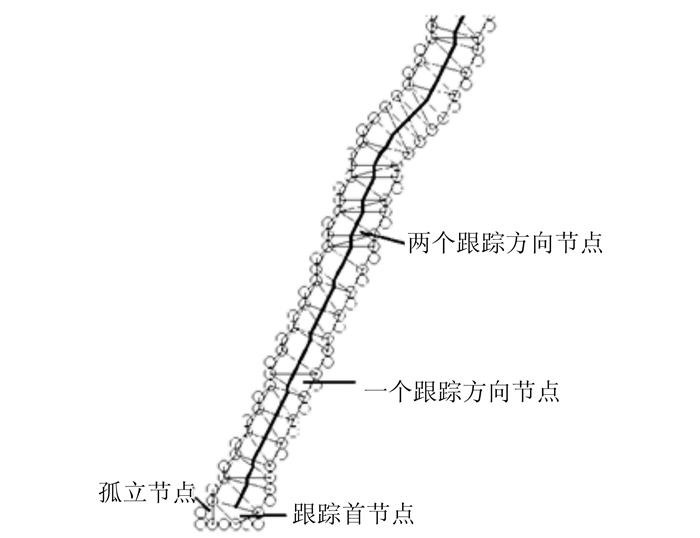
1) 获取当前处理中的线划要素边缘点集三角网中的首三角形。由于在§2.1中剔除了干扰三角形,致使某些三角形成为孤立的三角形(如图 6所示)。因此,需通过判断每个三角形的拓扑邻接指针是否全为空,识别出独立三角形。若某一三角形为独立三角形,则通过此三角形节点的next指针跳过此孤立三角形,并置这个三角形的访问处理标识为真。
2) 判断此三角形是否已被处理。如果访问处理标识为真,则表示此三角形已被处理过,需跳过,此时取当前三角形的next指针值,作为下一个要处理的三角形;当此next指针为空时,则跳出骨架线追踪循环,准备处理下一个线划对象。
|
| 图 6 骨架线追踪过程示意图 Fig. 6 Diagram of Process in Skeleton Line Trace |
3) 如果当前三角形既不是孤立三角形、也不是已处理过的三角形,则根据此三角形拓扑邻接状态,即统计与此三角形拓扑相连且未被处理过的三角形个数,决定追踪策略。
(1) 未处理的邻接三角形个数为1,表明骨架线追踪方向确定且唯一。通过获取当前追踪三角形与邻接三角形公共边中点,即可得到线划要素骨架线点。最后置此邻接三角形访问处理标识为真,并设该三角形为当前追踪三角形。
(2) 未处理的邻接三角形个数为2,则说明此时骨架线的跟踪顺序不确定,需决定跟踪方向,处理过程基本同上,不同的是此时潜在追踪方向有2个。由于Delaunay三角网单体沿垂直于线划伸展方向展开(狭长型),因而选择两边中的较长边,作为追踪边,即可确保跟踪正确。若两边长度相同,则根据Delaunay三角形在三角网中的拓扑生成顺序,选择拓扑关系较先建立的三角形,作为追踪三角形。
(3) 未处理的邻接三角形个数为0,表示当前追踪三角形已无追踪方向,需跳跃到可进行追踪操作的三角形,继续进行骨架线追踪操作。此时置当前三角形访问处理标识为真,并获取其next指针所指向的三角形作为追踪三角形。如果当前三角形next指针为空,则表示此线划对象中所有的Delaunay三角形都已进行了骨架线追踪处理,此时则跳出骨架线追踪循环,准备处理下个线划对象4重复(1)~(3)步直到当前三角形节点的next指针为空,停止此条线划的骨架线追踪,准备处理下一个线划对象。
3 实验及结果分析单扫描线划为实验对象,进行矢量化操作,并对各主要处理阶段的结果加以展示,如图 7所示。图 7(a)为原始栅格线划图像,由一条基本线划和圆组成。图 7(b)~图 7(f)为线划要素矢量化过程中,各主要环节的处理结果。图 7(b)表示的是要素连通性识别结果,图中互不相连的两个线划对象,用不同灰度值加以区分。图 7(c)为线划要素边缘提取结果,线划边缘轮廓齐整连续且为单像素宽,生成边缘要素点分布均匀,可较好地表征线划要素边缘。图 7(d)和图 7(e)分别为线划要素边缘点集生成的原始三角网和经剔除干扰三角形后的三角网,生成的三角网沿线划要素边缘均匀展开。图 7(f)展示了线划要素矢量化的最终结果,提取的线划要素骨架线,基本上沿线划要素伸展方向展开,形状良好,与原始栅格线划有较高的匹配度。

|
| 图 7 骨架线提取各主要阶段结果 Fig. 7 Results of Skeleton Line Extraction in Each Main Phase |
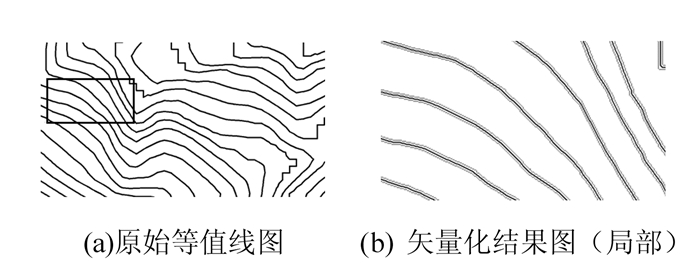
为了进一步对本文所述方法进行性能检测,选取了同一景图像不同幅面的栅格等值线图作为实验对象(如图 8(a)所示),在HP Z600图形工作站(CPU: Xeon 5606 内存12 GB)上进行实验,记录各主要处理阶段的时间代价。为了排除实验平台中偶然因素的干扰,采取了多次实验求平均值的方式,以确保实验数据的准确性。该幅图像由23条栅格线划组成,实验结果如表 1和图 8所示。
|
| 图 8 栅格线划图矢量化 Fig. 8 Vectorizaiton of Grid Line Map |
|
图像尺 寸/像素 | 边缘栅格 点数量/个 | 图像二 值化/ms | 线划要素 识别/ms | 边缘点集 生成/ms | Delaunay三角 网生成/ms | 剔除干扰三 角形/ms | 骨架线追踪 |
| 3 144×1 728 | 94 048 | 47 | 517 | 203 | 762 | 16 | 16 |
| 4 192×2 307 | 129 062 | 95 | 924 | 341 | 1 260 | 16 | 16 |
| 5 240×2 880 | 164 076 | 125 | 1 401 | 542 | 2 030 | 31 | 16 |
从表 1中数据可知,随着图像幅面的增大,基于栅格图像分析的算法(表 1中第三列~第五列)的时间代价显著增加,而骨架追踪算法(表 1中第七列、第八列)的时间代价则基本保持不变,其算法时间代价应与图像的复杂程度(即线划个数)有关,而与线划宽度无关。因此,本文所提出的骨架线追踪方法更适宜处理线划宽度较宽的扫描图像。在一次矢量化处理过程中,Delaunay三角网生成的时间代价最大,而骨架线追踪算法的耗时尚不到其十分之一。文本所采用Delaunay三角网生成算法是较为经典的扫描线算法[18],而这部分时间代价可用最新的研究成果加以优化改进,大幅缩短处理时间。因此,本文所提出的栅格线划矢量化方法仍有较高的时间效率。
在算法设计策略上,本文所提出的方法与已有方法也有些许差异:(1)已有的骨架线提取方法是对整个图像区域生成约束Delaunay三角网[11, 12, 14],而本文方法是先进行线划要素识别,再进行无约束的Delaunay三角网生成。首先,无约束Delaunay三角网生成效率要比约束Delaunay三角网高;其次,随着图像幅面逐渐增大,Delaunay三角网生成算法的时间代价大幅上升(复杂算法的时间复杂度一般不是线性的,最好情况下为O(nlog2n),而通过对线划要素识别,可把一个复杂点集按线划对象分为若干子集,对这些子集分别进行Delaunay三角网生成,也可大幅提高算法效率。(2)已有骨架线提取方法提取骨架线后,还要进行拓扑连接等后续处理[11, 12, 14],而本文方法通过追踪三角形公共边中点方式,一次性生成具有空间拓扑关系的骨架线,算法流程更为简洁,骨架线提取的准确度更高。
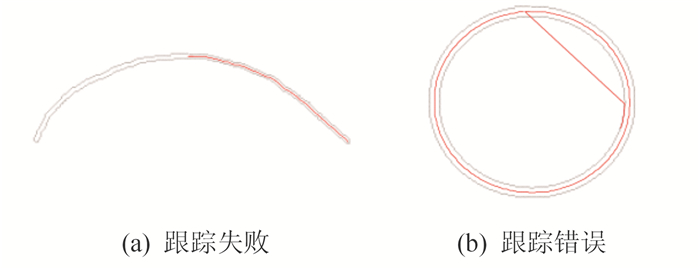
虽然本文方法能直接生成带空间拓扑关系的线划要素骨架线,但仍存在一些问题和不足。扫描线Delaunay三角网生成算法是针对空间离散点设计的,其初始三角形是由x、y坐标最小值点构成的[18]。本文方法就是基于此初始三角形进行骨架线追踪。但由于线划要素在像素空间中呈条状稀疏分布,而原始Delaunay三角网呈凸多边形面状分布,致使经剔除操作后的Delaunay三角网首节点不一定在线划要素的某一端点处;加之三角形节点存储顺序是按扫描线扫描顺序(从左向右、从下到上)存储,而不是沿线划伸展方向存储。如果经剔除处理后的三角网首节点不在线划要素某端点处,就会造成骨架线跟踪失败或跟踪丢失等情况,最终出现如图 9的不能完全提取或提取错误骨架线的状况。除此之外,扫描图像中还存在由于印制或扫描设备等因素造成的扫描线划宽度突然变化或折曲不自然等现象。在出现此类情况的线划部位,会产生极不规则的三角形。这些不规则的三角形,也会导致骨架线跟踪错误或跟踪失败。因此,为了进一步完善本方法,在进一步的研究工作中,应试图通过改变Delaunay三角网的生成方式或对经剔除操作后的Delaunay三角网进行重新组织,以解决如图 9所示的追踪错误问题;而形状不规则的三角形造成的追踪错误,则考虑设计出一种能自动跳过形状不规则三角形,并以此为追踪点重新开始骨架线追踪的追踪策略。
|
| 图 9 提取错示意图 Fig. 9 Extract Fault Diagram |
本文在分析现有基于Delaunay三角网骨架线提取方法研究的基础上,提出了一种基于Delaunay三角网的扫描线划矢量化方法。以基于Delaunay三角形公共边中点追踪的线划要素骨架线提取为技术核心,实现了扫描线划的矢量化操作,其算法时间效率、提取结果准确性较已有算法有所提高,能满足实际应用需求。
| [1] | Zou Xiuming, Zhang Yuexin. Research and Realization about Gird Map Vector[J]. Computer Engineering and Applications, 2003, 39(19):102-103(邹修明,张岳新. 栅格地图矢量化关键技术研究与实现[J]. 计算机工程与应用, 2003, 39(19):102-103) |
| [2] | Lin Zongjian, Lu Jian, Di Kaichang. A Computer Vision Based Thematic Map Reading System[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1992,(2):8-17(林宗坚,卢健,邸凯昌. 基于计算机视觉的专题图读取系统[J]. 武汉测绘科技大学学报, 1992,(2):8-17) |
| [3] | Chen Huanxin, Sun Qun, Liu Xingui, et al. Vectorization of Contour Line and Isobath from Tint Area in Combination Plate Map[J]. Geomatics and Information Science of Wuhan University, 2013,38(5):622-625(陈换新,孙群,刘新贵,等. 彩色扫描地图中背景色的等高(等深)线矢量化研究[J]. 武汉大学学报·信息科学版, 2013,38(5):622-625) |
| [4] | Lam L, Lee S,Suen C Y. Thinning Methodologies-a Comprehensive Survey[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1992, 14(9):869-885 |
| [5] | Hilditch C J. Comparison of Thinning Algorithms on a Parallel Processor[J]. Image and Vision Computing, 1983, 1(3):115-132 |
| [6] | Liu Yongjie, Cao Shunmao. Study of Map Vectorization Based on Ant Colony Optimization Algorithm[J]. Bulletin of Surveying, 2010, 3(3):35-37(刘永杰,曹顺茂. 基于蚁群算法的地图矢量化算法研究[J]. 测绘通报, 2010, 3(3):35-37) |
| [7] | Singh S, Amin A. Neural Network Recognition of Hand-printed Characters[J].Neural Computing & Applications, 1999, 8(1):67-76 |
| [8] | Kégl B, Krzyzak A. Piecewise Linear Skeletonization Using Principal Curves[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(1):59-74 |
| [9] | Han C, Fan K. Skeleton Generation of Engineering Drawings via Contour Matching[J]. Pattern Recognition, 1994, 27(2):261-275 |
| [10] | Chen Yong, YuanYuzheng. The Implementation of an Automatic Following Algorithm Based on Multiple Criteria[J]. Journal of Wuhan Technical University of Surveying and Mapping, 1995,2:178-181(陈勇,袁宇正. 一种基于多重判据的自动跟踪算法的实现[J]. 武汉测绘科技大学学报, 1995,2:178-181) |
| [11] | Hu Wei, Tao Weidong, Yuan Zhenyu, et al. A Method of Vectorization of Scanning Map Based on Voronoi Diagrams[J]. Geomatics and Information Science of Wuhan University, 2013, 38(4):470-474(胡玮,陶伟东,苑振宇等. 一种Voronoi图的扫描地图矢量化方法[J]. 武汉大学学报·信息科学版, 2013, 38(4):470-474) |
| [12] | Ai Tinghua, Guo Renzhong. Extracting Center-lines and Building Street Network Based on Constrained Delaunay Triangulation[J]. Acta Geodaetica et Cartographica Sinica, 2000,(4):348-354(艾廷华,郭仁忠. 基于约束Delaunay结构的街道中轴线提取及网络模型建立[J]. 测绘学报, 2000,(4):348-354) |
| [13] | Chen Tao, Ai Tinghua. Automatic Extraction of Skeleton and Center of Area Feature[J]. Geomatics and Information Science of Wuhan University, 2004,29(5):443-446(陈涛,艾廷华. 多边形骨架线与形心自动搜寻算法研究[J]. 武汉大学学报·信息科学版, 2004,29(5):443-446) |
| [14] | Ai Tinghua. A Spatial Field Representation Model Based on Delaunay Triangulation[J]. Acta Geodaetica et Cartographica Sinica, 2006,(1):71-76(艾廷华. DELAUNAY三角网支持下的空间场表达[J]. 测绘学报, 2006,(1):71-76) |
| [15] | Wu Xiaobo, Wang Shixing, Xiao Chunsheng. A New Study of Delaunay Triangulation Creation[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(1):28-35(武晓波,王世新,肖春生. Delaunay三角网的生成算法研究[J]. 测绘学报, 1999, 28(1):28-35) |
| [16] | Zhang Xiujun, Guo Xia, Jin Xinyu. The Pixel Labeled Algorithm with Label Rectified of Connecting Area in Binary Picture[J]. Journal of Image and Graphics, 2003, 8(2):198-202(张修军,郭霞,金心宇. 带标记矫正的二值图象连通域像素标记算法[J]. 中国图象图形学报, 2003, 8(2):198-202) |
| [17] | Zhang Xiang, Liu Meijie, Chen Liwei. Method of Picking up Edge on the Basis of the Mathematics Morphologic Subject[J]. Journal of UEST of China, 2002,(5):490-493(张翔,刘媚洁,陈立伟. 基于数学形态学的边缘提取方法[J]. 电子科技大学学报, 2002,(5):490-493) |
| [18] | Fortune S. Asweepline Algorithm for Voronoi Diagrams[J]. Algorithmica, 1987, 2(1-4):153-174 |
| [19] | Mccullagh M J, Ross C G. Delaunay Triangulation of a Random Data Set for Isarithmic Mapping[J]. The Cartographic Journal, 1980, 17(2):93-99 |
| [20] | Rui Yikang, Wang Jiechen. A New Study of Compound Algorithm Based on Sweepline and Divide-and-conquer Algorithms for Constructing Delaunay Triangulation[J]. Acta Geodaetica et Cartographica Sinica, 2007,(3):358-362(芮一康,王结臣. Delaunay三角形构网的分治扫描线算法[J]. 测绘学报, 2007,(3):358-362) |
 2016, Vol. 41
2016, Vol. 41



