文章信息
- 张朋东, 石岩, 邓敏, 赵玲
- ZHANG Pengdong, SHI Yan, DENG Min, ZHAO Ling
- 基于拓扑强度的城市道路网络层次表达
- Hierarchical Representation of Urban Road Network Based on Topological Intensity
- 武汉大学学报·信息科学版, 2016, 41(2): 178-183,213
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 178-183,213
- http://dx.doi.org/10.13203/j.whugis20130798
-
文章历史
- 收稿日期: 2014-10-01

城市道路网络是每个城市不可或缺的基础设施,对于一个城市的交通运行起着至关重要的作用[1]。城市道路网络的结构特性是城市道路网络表达的基础,并且对于进一步深入分析城市交通的运行状况非常重要[2]。随着对复杂网络研究的兴起和深入,复杂网络理论已成为对各种网络进行分析的主要工具。与此同时,小世界(small-world)特性[3]和无标度(scale-free)特性[4]的发现更加掀起了对复杂网络理论的研究热潮[5, 6, 7, 8, 9]。
近十年来,复杂网络理论已开始应用于城市道路网络分析,并取得了一些进展,主要集中在两个方面:①研究城市道路网络的小世界特性和无标度特性。Porta等[10]对具有不同形态和历史背景的6个城市的道路网络进行拓扑分析,发现它们均为无标度网络,并且表现出了小世界特性;Jiang[11]选取了美国40个城市的道路网络进行分析,发现它们均具有小世界特性和无标度特性;Crucitti等[12]将所研究的城市分为自组织型和规划型两种,然后采用中心性指标对其道路网络进行分析,结果表明具有和非空间网络几乎一致的无标度性;Sienkiewicz等[13]对波兰22个城市的道路网络进行了研究,发现所有网络均展现出小世界特性,部分网络的度还符合幂律分布,即具有无标度性;吴建军[14]研究了北京市道路网络,揭示了其无标度特性。②研究城市道路网络的抗毁性和鲁棒性。李英等[15]对上海市道路网络进行了抗毁性分析和实验;张勇等[16]以合肥市道路网络为例,进行了路网可靠性仿真分析。以上两方面研究中,小世界特性及无标度特性为基础性研究,路网抗毁性及鲁棒性则为深入性研究。此外,也有学者利用复杂网络理论对城市道路网络的某一特性进行了专门分析,如李清泉等[17]对国内6个城市的道路中介中心性进行了分析,结果表明其分布呈现一定的规律,具有等级性。
总结分析可以发现,现有的研究大多是以整个道路网络为研究对象,研究的均为网络的整体性质(如小世界特性、无标度特性、抗毁性及鲁棒性等)。实际情况中,每条道路在路网中所起的作用并不完全相同。例如,某条道路的破坏将使得整个路网的连通性消失,即分为若干孤立的道路子网;而另一条道路的破坏对整个路网几乎没有影响。在这种情况下,仅研究道路网络的整体性质将丢失每条道路对整体路网的贡献情况,因而需要深入研究每条道路在维持整个路网拓扑连通性方面的能力。鉴于此,本文将以每条道路为研究对象,着重研究单条道路在维持路网拓扑连通性方面的能力,即拓扑强度,进而提出一种对拓扑强度进行层次表达的模型。该模型可准确描述每条道路在整体路网的重要性程度,从而在进行重要道路保护、修建、规划等方面提供参考,尤其在地震、强降水等恶劣条件下有利于保证城市道路网络的正常连通和城市交通的顺利运行。
1 拓扑强度与道路网络层次 1.1 路段拓扑强度分析在网络分析领域,通常用抗毁性、鲁棒性、可靠性等词语来描述整体道路网络在拓扑方面的稳定度,而针对每条路段则需要用一个准确的词语来描述其对整体路网抗毁性、鲁棒性或可靠性的贡献程度,为此,本文提出拓扑强度的概念。
定义1 拓扑强度(topological intensity,TI):给定任一路段rsi,其在维持整体路网拓扑连通性方面的能力称为路段rsi的拓扑强度TI(rsi)。TI(rsi)越大,路段rsi的拓扑强度越强,若路段rsi失效,整体路网连通性遭到破坏的概率越小;反之,TI (rsi)越小,路段rsi的拓扑强度越弱,若路段rsi失效,整体路网连通性遭到破坏的概率越大。为详细分析整体路网中各路段的拓扑强度,本文提出以下研究策略。
1) 采用对偶法[10, 18]对城市交通路网进行建模,将其抽象为网络拓扑关系图;
2) 基于复杂网络理论对生成的网络拓扑关系图分别计算图中各节点的节点度、中介中心度和接近中心度;
3) 采取节点攻击策略对网络拓扑关系图中的节点进行破坏,并分析网络攻击结果;
4) 根据网络攻击结果,分析每条道路的拓扑强度。
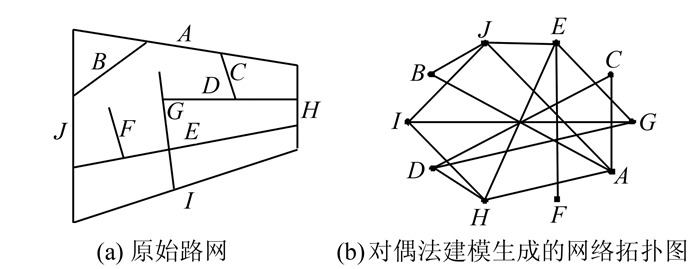
1.1.1 对偶法建模给定整体道路网络,将路网中的每条道路抽象为网络中的一个节点,将道路之间的联系抽象为网络的边,得到相应的网络拓扑关系图。若两条道路相连,则表示网络拓扑关系图中相对应的两个节点相连,否则,两节点间没有连接。如图 1(a)为原始路网,图 1(b)为对原始路网采用对偶法建模后生成的网络拓扑关系图,包含A、B、C、D、E、F、G、H、I、J共10个节点。
|
| 图 1 对偶法建模示例 Fig. 1 An Example of Modeling with Dual Approach |
为了度量每条路段的拓扑强度,需要定义一系列度量指标。经过对偶图建模后,路段的拓扑强度可类比于复杂网络理论中的节点重要性,因此,本文采用与复杂网络理论中度量节点重要性类似的指标[18, 19]度量路段的拓扑强度。
定义2 节点度(node degree,ND):给定网络拓扑关系图(network topological graph,NTG),对于任一节点ni,与ni直接相连的所有节点记为CN(ni),那么ri的节点度可表达为:

式中,|CN(ni)|表示与节点ni直接相连的节点个数。节点ni的节点度ND(ni)越大,表示与ni相连的道路条数越多,在一定程度上表明该道路越重要。如图 1所示,节点A的节点度为4,表示有4条路段与路段A相连,即路段B、C、H、J。
定义3 中介中心度(betweenness centrality degree,BCD):对于包含N个节点的NTG中的两个节点ni和nj,ni到达nj有多条路径,其中ni和nj之间的最短路径为经过最少边数的一条路径,如图 1所示,节点A到达G至少需要经过AJ、JE、EG 3条边,即节点A和G间的最短路径为3。为了度量节点ni连接其它节点的能力,定义其中介中心度为:
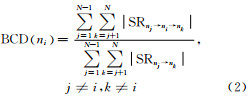
式中,|SRnj→ni→nk|表示节点nj到nk之间最短路径中同时经过节点ni的数量;|SRnj→nk|表示从节点nj到节点nk的路径总数。节点nj的中介中心度越大,表明在整体路网中经过此路段的最短路径越多,即此路段的“桥梁”作用越显著。如图 1中,对于节点A,经过计算,两两节点间(除节点A)共60条最短路径,其中经过节点A的最短路径有B→A→C、B→A→C→D、B→A→H→D、B→A→H、C→A→H→E、C→A→J→E、C→A→H→E→F、C→A→J→E→F、C→A→H、C→A→H→I、C→A→J→I、C→A→J、D→C→A→J、D→H→A→J、H→A→J 15条,因此BCD(A)=15/60=1/4。
定义4 接近中心度(closeness centrality degree,CCD):对于节点ni,为度量ni在整体网络中与其它节点的接近程度,定义其接近中心度为:
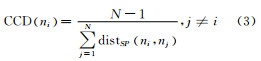
式中,distSP(ni,nj)表示节点ni与nj之间的最短路径长度。节点ni的接近中心度越大,表明ni到其它节点的最短路径越短,即节点ni越接近整体网络的重心。如图 1所示,N取值为10,其中节点A到其它节点的最短路径依次为A→B、A→C、A→H→D、A→J→E、A→J→E→F、A→J→E→G、A→H、A→J→I、A→J,即最短路径长度依次为1、1、2、2、3、3、1、2、1,因此,CCD(A)=(10-1)/(1+1+2+2+3+3+1+2+1)=9/16。
1.1.3 节点攻击对网络节点进行攻击有两种方式[20]:① 随机攻击,指对网络中的节点进行随机破坏;② 蓄意攻击,指按一定的策略对网络中的节点进行有目的的破坏。在多次攻击网络节点时,随机性攻击会得到各种不同的结果,盲目性较强,因而不适于确定节点的重要性。本文采取蓄意攻击策略,分别基于节点度、中介中心度和接近中心度对道路网络拓扑强度进行分析。
1) 基于节点度进行攻击。根据节点度的定义可知,节点度越大的节点失效,网络遭到破坏的概率越大,即该节点所代表的道路在路网中的拓扑强度越弱。因此基于节点度对网络进行攻击时,采取按节点度由大到小的策略逐点删除。
2) 基于中介中心度进行攻击。根据中介中心度的定义可知,中介中心度越大的节点失效,网络越容易分为两个或多个孤立子网,该节点所代表的道路在路网中的拓扑强度越弱。因此基于中介中心度进行攻击时,采取按中介中心度由大到小的策略逐点删除。
3) 基于接近中心度进行攻击。根据接近中心度的定义可知,接近中心度越大的节点失效,网络重心区域遭到破坏的概率越大,网络连通性越容易遭到破坏,该节点所代表的道路在路网中的拓扑强度越弱。因此基于接近中心度进行攻击时,采取按接近中心度由大到小的策略逐点删除。
1.1.4 攻击结果分析目前尚无度量网络拓扑连通性的通用指标,本文采用广泛应用的两个指标度量网络拓扑连通性,即网络平均路径长度和节点攻击前后的网络规模比[21]。通过分析攻击前后两个指标的变化曲线图,可得出网络拓扑连通性的变化情况。
定义5 网络平均路径长度(network average path length,NAPL):给定网络拓扑关系图(network topology graph,NTG),NTG的平均路径长度为网络中所有节点间最短路径长度的均值,可表达为:

式中,distSP(ni,nj)表示节点ni和nj之间的最短路径长度。网络的平均路径长度可用来描述网络中节点间的离散程度,网络平均路径长度越小,说明网络越紧密,反之,网络越稀疏。本文中网络平均路径长度特指网络中含节点数最多的连通子网的平均路径长度。
定义6 网络规模比(network size ratio,NSR):网络规模为网络的极大连通子网(maximum connect graph,MCG)中所包含的节点的个数,记为NSMCG。对道路网络拓扑关系图NTG进行节点攻击前后的网络规模比可表达为:

式中,NSMCGori为节点攻击前的网络规模;NSMCGatt为节点攻击后的网络规模。网络规模比越大,说明攻击后网络规模减小越多,即道路网络连通性遭到的破坏程度越大;反之,说明攻击后道路网络连通性遭到破坏的程度越小。
1.2 道路网络层次表达道路网络是由众多路段相互连接而成,本文的道路网络层次表达模型以路段拓扑强度的度量指标——节点度、中介中心度和接近中心度为基础,通过一定的数学运算求得,并最终以集合的形式进行表达。该模型的具体计算及表达过程如下:记原始路网中所有路段集合为RS,按节点度、中介中心度、接近中心度由大到小的次序对路段进行逐条破坏至路网恰好失去连通性,此时删除的路段集合分别表示为RSND、RSBCD和RSCCD,对RSND、RSBCD、RSCCD进行不同组合,可得到集合L1、L2、L3、L4:
L1= RSND∩RSBCD∩RSCCD
L2= (RSND∩RSBCD)∪(RSND∩RSCCD)∪(RSBCD∩RSCCD)
L3= (RSND∪RSBCD∪RSCCD)-L1-L2
L4= RS-L1-L2-L3
式中,L1、L2、L3、L4分别表示第一、二、三、四层次拓扑强度的路段集合,其大小为L1<L2<L3<L4。最终,基于拓扑强度的路段层次表达模型可表示为:
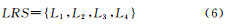
为了保证所建模型的正确性、合理性及有效性,需要对模型进行检验。本文对模型进行检验包含两个步骤:对原始道路网络进行节点攻击;对受攻击后的道路网络进行评价。对原始道路网络进行节点攻击时,分别按如下四种策略执行:① 按节点度由大到小的次序进行节点攻击,即从原始道路网中逐个删除与当前节点度值相对应的路段;② 按中介中心度由大到小的次序进行节点攻击,即从原始道路网中逐个删除与当前中介中心度值相对应的路段;③ 按接近中心度由大到小的次序进行节点攻击,即从原始道路网中逐个删除与当前接近中心度值相对应的路段;④按本文模型LRS由第一、二、三、四层次逐级进行节点攻击,即从原始道路网中逐个删除当前层次中的路段。对受攻击后的道路网络进行评价时,基于网络平均路径长度和网络规模比两个指标。具体表述为:对于每种攻击策略,每删除一条路段后,分别按式(4)和式(5)求取受攻击后的道路网络的网络平均路径长度和网络规模比两个指标值,直至所有路段删除完毕。对于每种攻击策略,其最终结果是得到相应的网络平均路径长度变化和网络规模比变化。最后,通过对网络平均路径长度和网络规模比指标变化进行综合分析与比较,实现对模型的有效性检验。
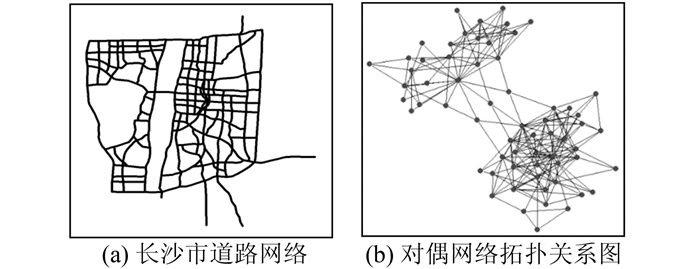
2 实验分析 2.1 实验数据实验数据采用湖南省长沙市道路网络,包含路段332条。对数据进行预处理,将名称相同的所有路段合并,生成63条新路段,如图 2(a)所示,对交通路网数据进行对偶法建模生成的网络拓扑关系如图 2(b)所示。
|
| 图 2 长沙市道路网络及其网络拓扑图 Fig. 2 Road Network of Changsha and Its Topological Graph |
道路网络中各路段的节点度、中介中心度和接近中心度见表 1。在网络拓扑关系中,分别按节点度、中介中心度和接近中心度由大到小的次序进行节点删除,得到的攻击结果如图 3所示。
| 节点ID | 节点度 | 中介中心度 | 接近中心度 |
| 8 | 21 | 0.125 971 7 | 0.410 596 0 |
| 11 | 18 | 0.329 376 8 | 0.427 586 2 |
| 3 | 17 | 0.241 562 8 | 0.466 165 4 |
| 19 | 13 | 0.057 656 0 | 0.385 093 2 |
| 29 | 11 | 0.021 324 9 | 0.378 048 8 |
 |  |  | 
|

|
| 图 3 道路网络攻击结果1 Fig. 3 The First Attacking Results of the Road Network |
分析图 3(a)发现:① 当按节点度由大到小的次序删除节点时,网络平均路径长度的整体变化趋势先逐渐增大至极大值,后呈下降趋势直至为零。这是由于删除的节点较少且网络连通性未消失,导致剩余网络的平均路径长度增大至某一极值。继续删除节点,使得网络连通性消失,此时网络平均路径长度为极大连通子网的平均路径长度,由于网络规模变小,使得网络平均路径长度逐渐减小为零。② 当按中介中心度由大到小的次序删除节点时,网络平均路径长度先逐渐增大至某一极大值后急剧减小,随后又逐渐增大至另一极大值,最后呈下降趋势直至为零。该曲线出现两个先增大后减小的过程,因此具有两个极大值,这是由于当网络平均路径长度达到第一个极大值以后,网络连通性消失。而继续删除节点时,极大连通子网能保持连通,因而使得网络平均路径长度会出现一次相似的变化过程。③ 当按接近中心度由大到小的次序删除节点时,网络平均路径长度的变化趋势与按中介中心度删除节点时基本一致。
通过分析图 3(b)可发现,分别按节点度、中介中心度和接近中心度由大到小的次序删除节点得到的三条曲线整体上均呈下降趋势,直至降为零,但期间均有若干急剧下降过程,这是由于初始阶段节点删除较少,网络依然保持连通性,因此网络规模逐渐减小,NSR值呈逐渐下降状态。当剩余节点数不足以保持网络连通性时,新网络规模更新为极大连通子网的规模,因此较原始网络规模急剧减小,使得NSR值突然迅速减小。
通过以上对NAPL值和NSR值变化曲线的分析可知,当NAPL值达到第一个极大值和NSR值发生第一次突变时,删除的节点个数为保持网络连通性的最大删除个数,此时按节点度、中介中心度、接近中心度删除的节点个数分别为19、7、4,RSND、RSBCD和RSCCD分别为:
RSND= { 8,11,3,19,29,32,33,39,7,26,28,36,37,46,10,14,55,61,62 }
RSBCD = { 11,3,40,63,8,39,2 }
RSCCD = { 3,40,63,2 }
结合本文提出的路段层次表达模型,可得到各层次的路段为:
L1 = { 3 }
L2 = { 40,63,2,39,11,8 }
L3 = { 62,19,28,33,61,29,37,46,32,26 36,10,14,7,55 }
L4 = { 4,25,41,51,5,21,35,42,45,13,16,44,58,48,49,50,53,1,17,12,23,54,20,43,22,24,47,60,15,30,34,38,56,57,18,27,52,31,59,6,9 }
LRS = {L1,L2,L3,L4}
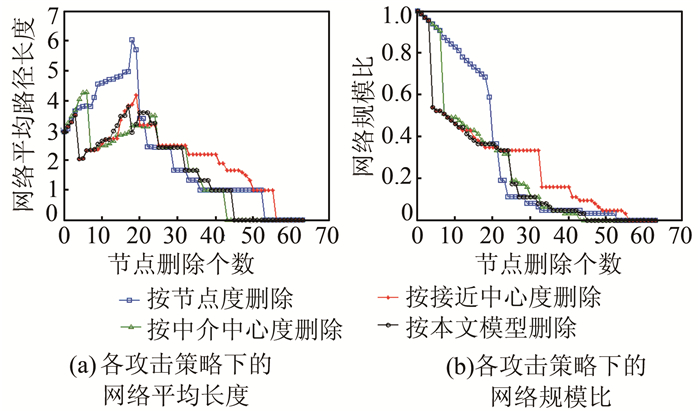
进而基于层次表达的路段对路网进行节点删除,得到的受攻击结果如图 4所示,其中图 4(a)、4(b)分别为按不同策略对网络攻击前后的NAPL值和NSR值变化曲线图,其中黑色曲线表示按本文模型对路网进行攻击后的结果。由图 4(a)、4(b)可以发现,按本文模型对网络节点进行删除时,相比其他三种攻击策略的网络连通性更易遭到破坏,说明本文模型更有效地提取出了维持路网连通性的必要节点以及网络中具有其他不同程度重要性的节点,是对按节点度、中介中心度和接近中心度得到的节点进行的必要的精细化,因此更加合理。
|
| 图 4 道路网络受攻击结果2 Fig. 4 The Second Attacking Results of the Road Network |
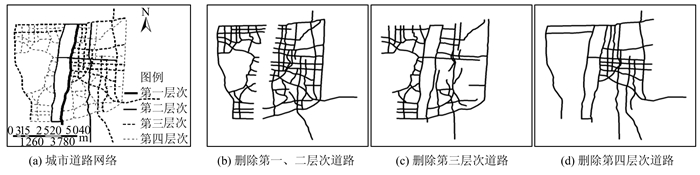
在城市道路网络中用不同符号表示不同的层次路段,如图 5(a)所示。进而通过删除不同层次的路段可视化表达剩余路网的连通性,如图 5(b)~5(d)所示。可以发现:① 第一层次和第二层次路段的拓扑强度相对较弱,这些路段的毁坏将导致整个路网连通性消失,所以需对此类路段进行重点保护;② 第三层次与第四层次路段的拓扑强度相对较强,若这些路段不能正常运行,整个路网连通性所受的影响相对较小;③第一层次与第二层次的路段数量较少,其它路段的拓扑强度较强,说明本文模型提取的重要性路段准确且更为精细,从而可以尽可能减少在保护重点路段时的花销。
|
| 图 5 城市道路网络层次表达 Fig. 5 Hierarchical Representation for the Urban Road Network |
本文以复杂网络理论为基础,以城市道路网络为研究对象,提出了一种基于拓扑强度分析的城市道路网络层次表达模型。通过该模型可以有效得出每条路段的拓扑强度等级,为确定各路段在维持路网连通性方面的重要性程度提供了必要依据。通过实际应用,证明了本文模型的正确性、合理性、有效性。进一步的工作主要集中在以下方面:①顾及路段长度、方向等特性,深入分析各路段在整体路网中的重要性;②结合交通流理论,将道路网络与交通流进行复杂耦合分析,以挖掘更深层次的城市交通规律。
| [1] | Li Deren, Li Qingquan, Yang Bisheng, et al. Techniques of GIS, GPS and RS for the Development of Intelligent Transportation[J]. Geomatics and Information Science of Wuhan University, 2008, 33(4):331-336(李德仁, 李清泉, 杨必胜,等. 3S技术与智能交通[J]. 武汉大学学报·信息科学版, 2008, 33(4):331-336) |
| [2] | Luan Xuechen, Yang Bisheng, Zhang Yunfei. Structural Hierarchy Analysis of Streets Based on Complex Network Theory[J]. Geomatics and Information Science of Wuhan University, 2012, 37(6):728-732(栾学晨, 杨必胜, 张云菲. 城市道路复杂网络结构化等级分析[J]. 武汉大学学报·信息科学版, 2012, 37(6):728-732) |
| [3] | Watts D J, Strogatz S H. Collective Dynamics of Small-world Networks[J]. Nature, 1998, 393(4):440-442 |
| [4] | Barabasi A L, Albert R. Emergence of Scaling in Random Networks[J]. Science, 1999, 286(5439):509-512 |
| [5] | Jeong H, Tombor B, Albert R, et al.The Large-scale Organization of Metabolic Networks[J]. Nature, 2000, 407(6804):651-654 |
| [6] | Holme P, Huss M, Jeong H. Subnetwork Hierarchies of Biochemical Pathways[J].Bioinformatics, 2003, 19(4):532-538 |
| [7] | Broder A, Kumar R, Maghoul F, et al. Graph Structure in the Web[J]. Computer Networks, 2000, 33(1):309-320 |
| [8] | Newman M E J. The Structure of Scientific Collaboration Networks[J].PNAS, 2001, 98(2):404-409 |
| [9] | Wasserman S, Faust K. Social Network Analysis[M]. Cambridge:Cambridge University Press, 1994 |
| [10] | Porta S, Crucitti P, Latora V. The Network Analysis of Urban Streets:A Dual Approach[J]. Physica A, 2006, 369(2):853-866 |
| [11] | Jiang B. A Topological Pattern of Urban Street Networks:Universality and Peculiarity[J]. Physica A, 2007, 384(2):647-655 |
| [12] | Crucitti P, Latora V, Porta S. Centrality Measures in Spatial Networks of Urban Streets[J]. Physical Review E, 2006, 73(3):036125 |
| [13] | Sienkiewicz J, Holyst J A. Statistical Analysis of 22 Public Transport Networks in Poland[J]. Physical Review E, 2005, 72(4):046127 |
| [14] | Wu Jianjun. Studies on the Complexity of Topology Structure in the Urban Traffic Network[D]. Beijing:Beijing Jiaotong University, 2008(吴建军. 城市交通网络拓扑结构复杂性研究[D]. 北京:北京交通大学, 2008) |
| [15] | Li Ying, Zhou Wei, Guo Shijin. An Analysis of Complexity of Public Transportation Network in Shanghai[J]. System Engineering, 2007, 25(1):38-41(李英, 周伟, 郭世进. 上海公共交通网络复杂性分析[J]. 系统工程, 2007, 25(1):38-41) |
| [16] | Zhang Yong, Yang Xiaoguang. Complex Network Property and Reliability Simulation Analysis of Urban Street Networks[J]. Journal of System Simulation, 2008, 20(2):464-467(张勇, 杨晓光. 城市路网的复杂网络特性及可靠性仿真分析[J]. 系统仿真学报, 2008, 20(2):464-467) |
| [17] | Li Qingquan, Zeng Zhe, Yang Bisheng, et al. Betweenness Centrality Analysis for Urban Road Networks[J]. Geomatics and Information Science of Wuhan University, 2010, 35(1):37-41(李清泉, 曾喆, 杨必胜,等. 城市道路网络的中介中心性分析[J]. 武汉大学学报·信息科学版, 2010, 35(1):37-41) |
| [18] | Jiang B, Claramunt C. A Structural Approach to Model Generalization of an Urban Street Network[J]. GeoInformatica, 2004, 8(2):157-171 |
| [19] | Newman M E J. The Structure and Function of Complex Networks[J]. SIAM Review, 2003, 45(2):167-256 |
| [20] | Albert R, Jeong H, Barabasi A L. Error and Attack Tolerance of Complex Networks[J]. Nature, 2000, 406(6794):378-382 |
| [21] | Holme P, Kim B J, Yoon C N, Han S K. Attack Vulnerability of Complex Networks[J]. Physical Review E, 2002, 65(5):056109 |
 2016, Vol. 41
2016, Vol. 41


