文章信息
- 付仲良, 杨元维, 高贤君, 赵星源, 逯跃锋, 陈少勤
- FU Zhongliang, YANG Yuanwei, GAO Xianjun, ZHAO Xingyuan, LU Yuefeng, CHEN Shaoqin
- 利用多元Logistic回归进行道路网匹配
- Road Networks Matching Using Multiple Logistic Regression
- 武汉大学学报·信息科学版, 2016, 41(2): 171-177
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 171-177
- http://dx.doi.org/10.13203/j.whugis20150112
-
文章历史
- 收稿日期: 2015-05-29

2. 长江大学地球科学学院, 湖北武汉, 430100;
3. 山东理工大学建筑工程学院, 山东淄博, 255049;
4. 浙江省测绘科学技术研究院, 浙江杭州, 310012
2. School of Geosciences, Yangtze University, Wuhan 430100, China;
3. School of Civil and Architectural Engineering, Shandong University of Technology, Zibo 255049, China;
4. Zhejiang Academy of Surveying and Mapping, Hangzhou 310012, China
随着空间信息获取与处理技术的快速发展,多源、多精度、多时相和多尺度空间信息的交换、融合与共享成为一种新的发展趋势。许多学者对矢量融合中地图合并(map conflation)展开研究,矢量匹配是地图合并中必不可少的关键步骤,道路网匹配是其中的一项研究热点[1]。如何对多源道路网数据进行有效融合,提高其综合质量及复用性,降低冗余,获得信息丰富、位置精确的道路网数据,更好地为电子地图、路径导航、LBS(location based service)等提供数据支持有重要价值。
国内外学者从空间和非空间信息对道路网特征进行了大量的研究,目前对道路网匹配方法的研究多集中在权值设定与阈值选取方面,主要可分为阈值法和模型法。阈值法主要利用道路节点或弧段的相似性特征组合直接结合匹配阈值构建匹配判定条件来识别同名道路。Saalfeld等基于“蜘蛛编码”规则,选取合适的匹配阈值,实现对道路节点的匹配[2];Gabay等利用点距和线段方向夹角共同作用进行匹配[3];Samal等提出了利用上下文实体匹配方法,通过构建的近似图的相似度比较来判定匹配[4];安晓亚等提出了一种基于结点和弧段的相似性度量的不同比例尺地图数据网状要素匹配算法[5];罗国玮等采用组合对象空间特征及语义特征进行综合比较的最优组合匹配法[6]。阈值法具有算法结构简单、耗时短、准确率相对较高等优点,但存在需要先验知识人工干预较多,数据针对性强等缺点。
模型法主要采用道路节点或弧段的相似性特征结合概率理论、迭代方法或数学模型等获取匹配结果。童小华等提出了基于概率理论的多指标匹配模型[7];巩现勇等利用蚁群算法的群体优势,寻找全局最优的道路网同名实体匹配方案[8];Li和Goodchild提出了基于最优化模型的全局同步匹配算法[9];Tong等运用最优化和迭代Logistic回归匹配算法实现道路网自动匹配[10]。模型法的特点是需要先验知识少、自动化程度高、数据适应性较强等,但在处理复杂匹配类型时能力相对较弱,算法耗时较长;其次,文献[9]中不能处理一对多的情况;文献[7]虽能处理一对多的情况但计算较为复杂;文献[8]中蚁群算法的信息挥发系数、最大搜索次数和蚁群规模等需要根据经验和多次试验确定;而文献[10]由于只采用单变量作为回归模型的自变量,导致其预测匹配结果对这个唯一变量过于敏感。
针对上述问题,本文提出一种多元Logistic回归匹配(multiple Logistic regression matching,MLRM)算法,通过选取并综合多种差异信息,能更有效描述道路待匹配对差异的多个不相似性特征,构建多元Logistic回归匹配模型,以预测出待匹配对之间的匹配概率,实现道路网的匹配。
1 多元Logistic回归的多特征融合匹配算法 1.1 不相似性计算描述道路待匹配对的不相似性特征很多,如形状、距离、语义、拓扑关系等。本文从形状、距离和语义三方面出发,结合道路的空间与非空间特征,设计了最小方向变化角、综合中值Hausdorff距离和语义差异三方面的特征,综合描述道路间的不相似性。
1.1.1 最小方向变化角线的方向变化角描述线形状的整体变化趋势,是描述线状实体相似性的一个重要特征。式(1)所示的正切角可有效表示线上各点的方向。

式中,θ(t)表示道路线在点t处正切线与水平方向所成的夹角;ω是参数t的单位间隔。
采用正切角比较两条道路方向差异的具体方法为:将待匹配道路线进行等分;利用式(1)计算待匹配道路线上各等分点的正切值;计算两条待匹配道路的方向变化角的差异。按待匹配道路的长度差异,其方向变化角差异的计算可分为两种情况。
情况一 当两条道路之间长度差异较小时(即length(lA)≤length(lB)≤2length(lA)或length(lB)≤length(lA)≤2length(lB),length(lA)和length(lB)是道路lA、lB的长度),采用在两条道路上选取相同数量的等分点并计算对应点之间的方向差异。
计算两条道路的方向变化角之差Orn_diff(lA,lB):
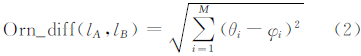
式中,θi、φi分别是指在线段lA、lB上的点i处的正切角;M是表示等分点的总个数。
情况二 当两条道路之间长度差异较大时(即length(lA)>2length(lB)或length(lB)>2length(lA)),具体计算步骤如下:① 假设较短道路为lA、较长的道路为lB;首先将lA均分,获取等分间隔Δl;②以lB的任一端点为初始等分的起始位置,采用间隔Δl对lB进行等分,得到道路lB子对象lB′j(j=0,1,2,…t),利用式(2)计算lA与lB′j之间的方向差异Orn_diff(lA,lB′j);③将lB′j的起始位置的游标整体移到下一个等分点,j=j+1,获取新的道路子对象lB′j+1并与lA进行比较。以此类推,直到j=t,即完成lA与lB的比较。取Orn_diff(lA,lB′j)的最小值作为lA与lB的方向变化角之差。以图 1为例,其中短道路点集pA = {b1,b2,b3,b4,b5,b6}和长道路点集pB = {p1,p2,…,p26}。循环比较时,先取点集pA与点集pB中的p1到p6组成的子对象pB1进行比较,然后,将pB1中游标整体将向下移一个等分点得到由p2到p7组成新对象pB2,将pA与pB2进行比较,以此类推,直至完成点集pA与点集pB中的p20到p26的比较,取最小值作为最终结果。

|
| 图 1 两条道路长度差异较大时变化角比较示意图 Fig. 1 Schematic Diagram of Comparing Change Angles when Large Differences Between Two Roads |
综合来说,两条道路的整体最小方向变化角如式(3)所示:

式中,N表示lA与lB的等分点总个数之差;Orn_diffk(lA,lB)表示第k次比较获取的最小方向变化角;Orn(lA,lB)表示两条道路的整体最小方向变化角。
1.1.2 综合中值Hausdorff距离空间距离是度量空间对象之间相对位置的重要参数,同时可作为描述对应实体的不相似性的重要特征。Hausdorff距离常用于描述线对象之间距离,但由于其取极值原理,致使无法有效表达线对象之间平均距离。中值Hausdorff距离较好表达道路对象之间的距离分布主趋势[11],但不适用于道路对象长度异常,尤其是距离差异较大的情况,而文献[10]提出的较短中值Hausdorff距离通过从较短线对象到较长线对象的有向距离解决了这一异常情况,但其未考虑垂足不在对应的线段上时造成的距离不准确问题,且无法处理复杂道路类型。因此,本文提出一种以欧氏距离和垂直距离为基础的综合中值Hausdorff距离(mixed median Hausdorff distance,MM_HD)。其基本思想是,作一条道路子对象端点到另一条道路子对象的垂足,若垂足点位于对应线段上,则采用垂直距离;若位于其延长线上,则将采用欧式距离。综合中值Hausdorff距离计算如式(4)所示:
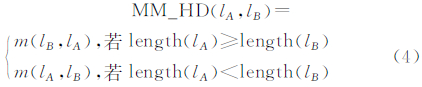
式中,length(lA)和length(lB)分别表示线要素lA和lB的长度;m(lB,lA)、m(lA,lB)分别为lB到lA、lA到lB的综合中值Hausdorff距离,如式(5)、(6)所示。
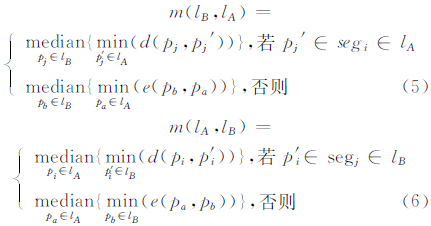
式中,pi和pj分别是lA和lB上的节点;p′i和p′j分别是pi和pj在lB和lA的垂足;pa和pb分别是lA和lB上的任意点;d(pj,p′j)表示pj到p′j的垂直距离;e(pb,pa)表示pb到pa的欧氏距离。以length(lA)≥length(lB)为例,当垂足p′j在lA的第i个子对象线段segi上时,取pj到p′j的垂直距离,m(lB,lA)=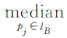 {
{ (d(pj,p′j))};否则m(lB,lA)=
(d(pj,p′j))};否则m(lB,lA)= {
{ (e(pb,pa))}
(e(pb,pa))}
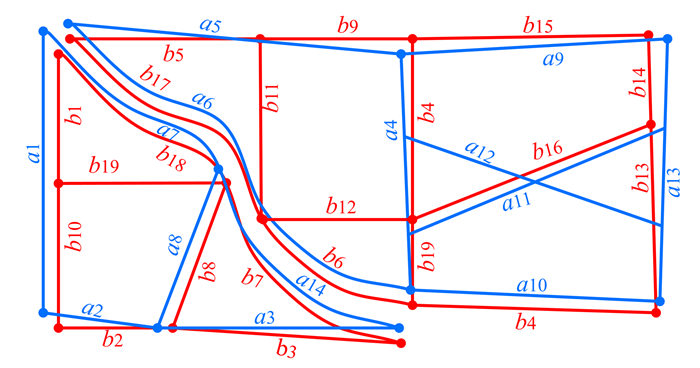
对如图 2所示,测试数据采用文献[10]中提出的SM_HD与本文提出的MM_HD,分别进行距离对比,结果如图 3所示。可以看出,在图中大部分待匹配对的距离描述上,两者的描述能力相当。但在部分待匹配对上存在明显的差异:① 如SM_HD(a11,b16)= 10.31,MM_HD(a11,b16)= 10.34;SM_HD(a12,b16)= 5.37,MM_HD(a12,b16)= 34.54,从匹配对a11∶b16与非匹配对a12∶b16的距离得出MM_HD分析错误匹配的能力更强;② 待匹配对a6∶b6、a6∶b17、a7∶b7、a7∶b18为曲线类型,SM_HD未能处理该类型(给定一个不被视为匹配的极大距离常量,图中这一距离常量为100 m),而MM_HD可以正常处理这一情况。综上所述,在描述道路距离方面的综合能力MM_HD要优于SM_HD。
|
| 图 2 待匹配测试数据图 Fig. 2 Diagram of Matching Data |

|
| 图 3 SM_HD与MM_HD的距离的对比图 Fig. 3 Comparison Roads of the Distance Values Between the Matching Pairs Using the SM_HD and MM_HD |
在现实世界中同一地理对象可能有多种属性表达方式,这种现象导致语义异构,并造成不同数据集中属性不一致。语义匹配是识别语义异构的方法,其具有计算简便、可靠性高等特点。因此,本文进一步采用语义差异来描述道路之间的不相似性。运用语义信息依赖于数据的质量和数据本身的特征。本文具体采用编辑距离来表达语义差异,该距离是通过计算从原字符串转换到目标字符串所需要的最少的字符插入、删除和替换的编辑次数[12]。语义差异综合计算公式如式(7)。
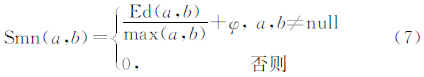
式中,a与b代表两个待匹配的字符串;Ed(a,b)表示编辑距离;max(a,b)表示其中字符较长的字符串。如果他们的属性不完整,则Smn(a,b)=0。φ为极小常量,它的存在是为了区分当出现空值字段后取的语义差异为零的情况。
通过上述方法,可获取道路网对象的3个不相似性特征计算,并组成3×N(N表示待匹配对的数量)的矩阵,然后根据这一矩阵构建多元Logistic回归模型。
1.2 多元Logistic回归模型匹配结果预测Logistic回归模型主要解决二分因变量(即1或0)分类问题,根据这一特征,可将其用到道路待匹配对分类(即“匹配”或“非匹配”)。预测待匹配对之间的匹配概率,进而判断匹配结果。
以往匹配方法中常采用单元Logistic回归模型匹配,计算简单,但由于其分类实质上采用固定值,易导致预测匹配概率值过于依赖单变量。当数据情况复杂时,单变量无法有效表达待匹配对之间的差异,而采用多变量的方式构建多元Logistic回归匹配模型可从多个方面共同预测匹配概率,减少对某一变量的过度依赖,能够有效克服单元逻辑回归模型的缺陷,能用于含有更复杂道路数据的道路网的匹配中。
依据Logistic回归的规则,匹配变量T表示二分变量(T=1或T=0)。假设待匹配对之间是匹配关系,那么T=1;反之,则T=0。当匹配事件发生T=1则匹配预测概率可以表达为P(T=1),它也表达条件匹配的概率。假设用k个自变量X1,X2,…,Xk表示去预测匹配变量(T),预测匹配概率为:
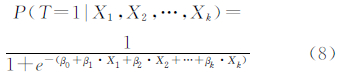
中,回归系数β1、β1、β2、…、βk 采用最大似然估计法进行计算。因此,估计模型(即预测匹配概率)为:

式中,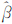 0、
0、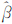 1、
1、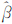 2、…、
2、…、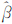 k分别是β0、β1、β2、…、βk的估计值,结合本文方法原理,设定k=3;自变量X1、X2、X3分别代表最小方向变化角、综合中值Hausdorff距离、语义差异,
k分别是β0、β1、β2、…、βk的估计值,结合本文方法原理,设定k=3;自变量X1、X2、X3分别代表最小方向变化角、综合中值Hausdorff距离、语义差异,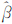 1、
1、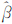 2、
2、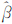 3分别是此三个自变量的回归系数的估计值。在预测匹配概率的过程中,割点概率z=0.5,以割点为界,可根据两条道路间最大似然估计匹配概率划分匹配与否的结果。如果P≥z,那么两条道路被视为匹配;反之,则不匹配。
3分别是此三个自变量的回归系数的估计值。在预测匹配概率的过程中,割点概率z=0.5,以割点为界,可根据两条道路间最大似然估计匹配概率划分匹配与否的结果。如果P≥z,那么两条道路被视为匹配;反之,则不匹配。
匹配算法的实现步骤
本文利用多元Logistic回归的道路网匹配算法的具体步骤如下。
(1) 选定参考数据集和待匹配数据集;
(2) 获取两个数据集实体信息,获取等分点数据;并根据实体信息构建拓扑关系,获得节点和弧段;
(3) 根据两幅地图的比例尺和精度等信息确定同名点的最大距离偏差ε;
(4) 根据最大距离偏差ε在参考数据集中寻找所有候选匹配道路;
(5) 按照式(3)、式(4)和式(7)计算待匹配对之间的不相似性,组成不相似性特征矩阵;
(6) 将获得的结果按照式(8)构建多元Logistic回归模型;
(7) 根据计算出的回归系数,预测待匹配数据集的匹配概率。
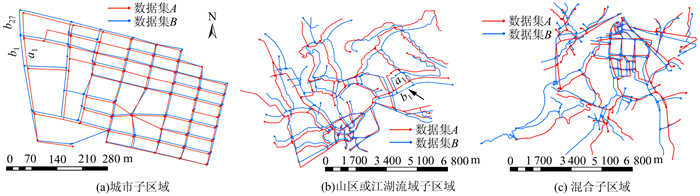
3 实验分析本文选取浙江省同一地区不同时相的道路网数据集进行实验验证。通过Microsoft Visual Studio 2010(C#),ArcGIS Engine 10.1实现待匹配对之间的不相似性计算;通过Matlab 6.0实现模型构建及待匹配对的匹配概率预测。通过对多个试验区域的对比分析,选取了能充分描述算法测试结果三种类型的子区域。这三个子区域分别是城市子区域(CD)、山区或江湖流域子区域(ML)、混合子区域(MD),如图 4所示。为证明实际效果,对以上三区域分别采用本文方法、文献[9]中的Opt算法和文献[10]中的OILRM算法进行对比。从匹配准确率和算法复杂两方面来评价。
|
| 图 4 来自浙江省三个子区域的实测数据图 Fig. 4 Three Domains of Test Data from Zhejiang Province |
为了能够定量的分析匹配结果,本文选用如式(10)和式(11)所示的准确率和召回率进行评价。准确率P是指正确匹配对与总匹配对的比率;召回率R是指正确的匹配对与数据中实际的正确匹配对的比率:
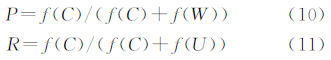
式中,f(C)表示正确的匹配数;f(W)表示错误的匹配数;f(U)表示漏匹配数。
通过选取的待匹配对样本训练构建了图 4(a)、图 4(b)、图 4(c)三个子区域的多元Logistic回归模型的回归系数、标准误差以及系数估计值的95.0%置信区间,见表 1。可以看出:① 回归系数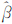 1、
1、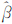 2、
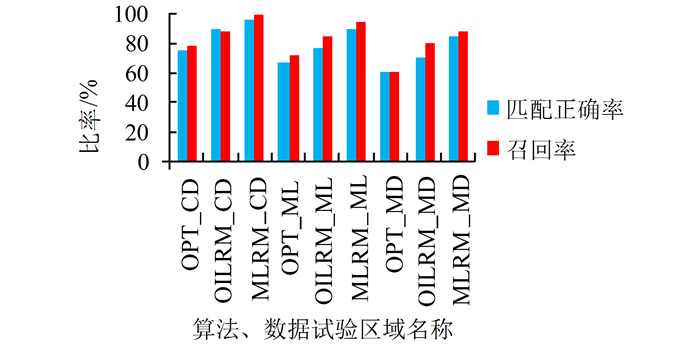
2、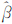 3的值均为正,说明参数对匹配都有着积极的作用;② 三个子区域之间的回归系数相当,最小方向变化角比综合中值Hausdorff距离与语义对模型的整体影响要小一些。表 2统计了数据集所含实体数量、语义完整度、正确匹配数、错误匹配数、漏匹配数、准确率和召回率。MLRM、OILRM和Opt三种方法在三个数据测试子区域的准确率和召回率对比如图 5所示。
3的值均为正,说明参数对匹配都有着积极的作用;② 三个子区域之间的回归系数相当,最小方向变化角比综合中值Hausdorff距离与语义对模型的整体影响要小一些。表 2统计了数据集所含实体数量、语义完整度、正确匹配数、错误匹配数、漏匹配数、准确率和召回率。MLRM、OILRM和Opt三种方法在三个数据测试子区域的准确率和召回率对比如图 5所示。
| 回归系数 | 城市 | 山区或江湖流经 | 混合 | |||||||||
| 估值 | 标准误差 | 95.0%置信区间 | 估值 | 标准误差 | 95.0%置信区间 | 估值 | 标准误差 | 95.0%置信区间 | ||||
| 下限 | 上限 | 下限 | 上限 | 下限 | 上限 | |||||||
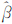 0 0 | -2.092 | 0.900 | -3.856 | -0.328 | -1.727 | 0.724 | -3.146 | -0.308 | -1.821 | 0.785 | -3.360 | -0.282 |
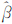 1 1 | 0.318 | 0.129 | 0.065 | 0.571 | 0.322 | 0.231 | -0.131 | 0.775 | 0.460 | 0.146 | 0.174 | 0.746 |
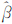 2 2 | 1.395 | 0.189 | 1.024 | 1.765 | 1.455 | 0.168 | 1.125 | 1.784 | 1.353 | 0.186 | 0.988 | 1.717 |
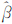 3 3 | 1.314 | 0.080 | 1.157 | 1.470 | 1.281 | 0.090 | 1.104 | 1.457 | 1.135 | 0.060 | 1.017 | 1.252 |
| 道路待匹配集 | 城市子区域 | 山区或江湖子区域 | 混合子区域 | ||||||
| 数据集A | 数据集B | 数据集A | 数据集B | 数据集A | 数据集B | ||||
| 道路对象总数 | 106 | 101 | 94 | 100 | 114 | 122 | |||
| 语义完整度/% | 60 | 42 | 56 | 34 | 56 | 46 | |||
| 算法名称 | Opt | OILRM | MLRM | Opt | OILRM | MLRM | Opt | OILRM | MLRM |
| f (C) | 86 | 86 | 97 | 64 | 71 | 85 | 69 | 78 | 92 |
| f (W) | 15 | 10 | 5 | 30 | 21 | 8 | 45 | 33 | 17 |
| f (U) | 12 | 12 | 0 | 24 | 12 | 5 | 44 | 20 | 12 |
| P(%) | 75.0 | 89.5 | 96.8 | 68.0 | 77.1 | 90.4 | 60.5 | 70.2 | 84.4 |
| R(%) | 78.5 | 87.7 | 100 | 72.7 | 85.5 | 94.4 | 61.0 | 79.5 | 88.4 |
从表 2和图 5得出以下结论。
|
| 图 5 三种方法在匹配正确率和召回率的对比情况 Fig. 5 Comparison of the Performances of the Three Matching Methods in Terms of Matching Accuracy and Matching Recall in the Study Area |
(1) MLRM、OILRM和Opt算法获得的匹配准确率依次降低。当测试数据集为城市道路数据时,三种方法的准确率都相对较高。当数据情况更复杂时,OILRM和Opt法匹配准确率明显下降,而本文提出的MLRM法几乎保持不变,原因为:① 本文采用的多元Logistic回归匹配模型比其他两种方法在分析错误匹配的能力要好。如图 4(b)中虚线箭头所指待匹配对a1∶b1被正确地检测出,而OILRM未检测出。其中MLRM法中Orn(a1,b1) = 0.551,MM_HD(a1,b1) =26.057,Smn(a1,b1) = 0.22,而OILRM方法中SM_HD(a1,b1)=26.06;② MM_HD比SM_HD更能够处理道路复杂情况(含有曲线或道路交叉口无交点),如图 4(a)中虚线箭头所指待匹配对a1∶b1与a1∶b27,OILRM法中,SM_HD(a1,b1) = 11.76和SM_HD(a1,b27) =7.83;而在MLRM法中,MM_HD(a1,b1) =11.79,MM_HD(a1,b27) = 62.34。可以看出,SM_HD(a1,b27)比SM_HD(a1,b1)的值小,所以OILRM法可能误判a1∶b27为匹配对而真匹配对a1∶b1被漏掉;MM_HD(a1,b27)比MM_HD(a1,b1)大许多,这样就可以有效避免误判情况发生;
(2) MLRM、OILRM和Opt法获得的匹配召回率都较高,尤其是后两种算法,原因是Opt算法未能处理非1∶1的情况,而OILRM算法无法有效处理复杂的道路网匹配类型。
选取较大的道路数据集为对象,该对象包含1 085个线实体(数据集A中548个线实体,在数据集B中,537个线实体,OILRM与Opt算法中逻辑回归样品则为294 276)。在准确率表现方面,Opt算法匹配准确率为346/537 = 64.4%;OILRM算法匹配准确率为476/537 = 88.6%。MLRM算法的准确率为493/537 = 91.8%。
3.2 复杂度评价假设m、n分别代表较小、较大的数据集所含实体数量,通过对Opt、OILRM、MLRM三种算法的复杂度进行分析可得:① 三者的时间复杂度分别为O(n2m)、O(n2m)+O(n)、O(k2m),k表示线实体等分点个数;② 在空间复杂度方面,由于OILRM算法在精炼匹配结果步骤中采用的自迭代算法,其空间复杂度为O(n),其他两种算法的空间复杂度均为O(1)。
三种算法在不同数据集规模的耗时对比实验见表 3。分析可知,当数据集规模不大时,Opt算法与OILRM算法在耗时上相当。原因是其核心为最优化算法,OILRM算法是在Opt算法的基础上增加了迭代Logistic回归过程,所以OILRM算法比Opt算法的耗时稍长,MLRM算法采用缓冲区搜索邻近对象使其寻优规模缩减至最小。当数据集规模增大时,Opt算法和OILRM算法的匹配耗时急剧增加,必须将其划分若干子区域进行匹配,以达到减少计算时间和保持匹配精度的目的,而无需进行分区处理,全局寻优规模缩减至最小的原理使得MLRM算法的耗时增长不明显。
| 数据集规模 | 耗时/s | |||
| 数据集A | 数据集B | Opt | OILRM | RLRM |
| 106 | 101 | 3.63 | 3.68 | 2.13 |
| 94 | 100 | 2.83 | 2.86 | 2.10 |
| 114 | 122 | 3.93 | 4.01 | 2.32 |
| 548 | 537 | 421.35 | 421.42 | 132.42 |
道路网匹配是道路网融合的重要一步。本文提出MLRM算法,首先设计了道路待匹配对之间最小方向变化角、综合中值Hausdorff距离和语义差异三种不相似性衡量指标,然后结合多元Logistic回归模型模拟道路匹配模型,准确地预测匹配结果,有效避免了组合特征间权值和匹配结果阈值的设定,且能处理道路类型复杂的情况(含有曲线或道路相交但无交点和非一对一情况),本文算法可应用于实际道路网的更新中。
| [1] | Yuan Tao S C. Development of Conflation Components[C]. Proceedings of Geoinformatics, Ann Arbor, 1999 |
| [2] | Saalfeld A. Conflation Automated Map Compilation[J]. International Journal of Geographical Information System, 1988, 2(3):217-228 |
| [3] | Gabay Y. Doytsher Y. Automatic Adjustment of Line Maps[C]. The GIS/LIS.94 Annual Convention, Arizona, Phoenix, USA, 1994 |
| [4] | Samal A, Seth S, Cueto K. A Feature-based Approach to Conflation of Geospatial sources[J]. International Journal of Geographical Information Science, 2004, 18(5):459-489 |
| [5] | An Xiaoya, Sun Qun, Yu Bohu. Feature Matching from Network Data at Different Scales Based on Similarity Measure[J]. Geomatics and Information Science of Wuhan University, 2012, 37(2):224-228(安晓亚, 孙群,尉伯虎. 利用相似性度量的不同比例尺地图数据网状要素匹配算法[J]. 武汉大学学报·信息科学版, 2012, 37(2):224-228) |
| [6] | Luo Guowei, Zhang Xingchang, Qi Lixin, et al. The Fast Positioning and Optimal Combination Matching Method of Change Vector Object[J]. Acta Geodaeticaet Cartographica Sinica, 2014, 43(12):1285-1292(罗国玮, 张新长, 齐立新,等. 矢量数据变化对象的快速定位与最优组合匹配方法[J]. 测绘学报, 2014, 43(12):1285-1292) |
| [7] | Tong Xiaohua, Deng Susu, Sui Wenzhong. A Probabilistic Theory-based Matching Method[J]. Acta Geodaeticaet Cartographica Sinica, 2007,36(2):210-217(童小华, 邓愫愫,史文中. 基于概率的地图实体匹配方法[J]. 测绘学报, 2007,36(2):210-217) |
| [8] | Gong Xianyong, Wu Fang, Ji Cunwei, et al. Ant Colony Optimization Approach to Road Network Matching[J]. Geomatics and Information Science of Wuhan University, 2014, 39(2):191-195(巩现勇, 武芳, 姬存伟,等. 道路网匹配的蚁群算法求解模型[J]. 武汉大学学报·信息科学版, 2014, 39(2):191-195) |
| [9] | Li L, Goodchild M. Automatically and Accurately Matching Objects in Geospatial Datasets[J]. Adv. Geo-Spat. Inf. Sci, 2010, 10:71-79 |
| [10] | Tong X, Liang D, Jin Y. A Linear Road Object Matching Method for Conflation Based on Optimization and Logistic Regression[J]. International Journal of Geographical Information Science, 2014, 28(4):824-846 |
| [11] | Min Deng, Zhilin Li. Xiaoyong. Chen. Extended Hausdorff Distance for Spatial Objects in GIS[J]. International Journal of Geographical Information Science, 2007, 21(4):459-475 |
| [12] | Navarro G. A Guided Tour to Approximate String Matching[J]. ACM Computing Surveys (CSUR), 2001, 33(1):31-88 |
 2016, Vol. 41
2016, Vol. 41



