文章信息
- 李佳田, 罗富丽, 余莉, 张蓝, 康顺, 林艳
- LI Jiatian, LUO Fuli, YU Li, ZHANG Lan, KANG Shun, LIN Yan
- 梯度Voronoi图及其构建算法
- The Gradient Voronoi Diagram and Construction Algorithm
- 武汉大学学报·信息科学版, 2016, 41(2): 163-170
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 163-170
- http://dx.doi.org/10.13203/j.whugis20140025
-
文章历史
- 收稿日期: 2014-07-09

2. 中国矿业大学(北京)地球科学与测绘工程学院, 北京, 100038;
3. 中国人民公安大学警务信息工程学院, 北京, 100038
2. College of Geoscience and Surveying Engineering, China University of Mining & Technology(Beijing), Beijing 100083, China;
3. Policing Information Technology College, People's Public Security University of China, Beijing 100038, China
Voronoi图是空间剖分的一种基础几何图形结构,它表现为一组生长元同时地向四周生长,直至相遇,所形成的各生长元空间势力范围的集合[1, 2]。Voronoi图蕴涵邻近与邻域等许多优良的空间概括性质,其被认为是研究和解决地理信息科学领域空间关系与空间分析[3, 4, 5, 6, 7, 8]、空间优化配置[9, 10]等相关问题的有力工具。学术界的普遍看法是将Voronoi图分为普通Voronoi图(ordinary Voronoi diagram,OVD)与权重Voronoi图(weight Voronoi diagram,WVD)两种基本类型。根据普通Voronoi图的定义,可将其认为是在理想平面之上的各生长元以统一速度均速生长的结果;对于生长元的整体来讲,构成权重Voronoi图的各生长元生长速度(权重)并非完全相同,而就某一个生长元,其生长速度在生长过程中通常是无变化的[11, 12, 13]。在以Voronoi图为基础的建模与分析中,诸多影响因素会使生长速度改变,而以恒定速度生长构成的Voronoi图较难有效地支持建模与分析中的客观条件,为此,增强Voronoi图的普适性,研究Voronoi图在非理想平面的生长特征与构建算法就成为一个必然需要解决的问题。
OVD是等距离边界构成的一种空间剖分,其是WVD的一个特例。WVD的权值作为初始条件被首先确定,其边界构成是权值比例下的等距离边界[14, 15, 16]。由于等距离边界并不随着客观条件的变化而改变,以此为切入点,本文将影响因素构建为权重距离函数,使生长速度一致地形式化为权重距离的时间导数,进而给出梯度Voronoi图的定义。以数学形态学为基础,用数字高程模型中单因素的高程变化为例,梯度Voronoi图的构建算法通过权重距离函数建立、变速膨胀过程与膨胀时间收敛三步聚顺序描述,旨在一般性地给出梯度Voronoi图的典型构建模型。在实际分析与建模中,如路网的优化配置中,对各方向上最优“阻抗”配送路线的选择,可依据梯度Voronoi所产生的势力范围获得最优解,而以恒定梯度构成的Voronoi并不能保证求解为最优。
1 梯度Voronoi图定义为了表达若干量在总量中的相对重要性,其被分别赋予不同的系数,则该系数被称为权重。权重是指某一指标项在整个指标项系统中的重要程度,它表示在其它指标项不变的条件下,某一指标项的变化对总量结果产生的影响。权重分为两类,即自重权与加重权。自重权是指以权数作为指标系统的分数,或者直接将权数作为等级的分值;而加重权则是指在各指标的已知分值(即自重权数)前面定义的权数。
以欧氏平面OVD与WVD的定义[3]为前提,总结权重距离,将权重值由常量形式转变为权重距离函数表达,使生长元的生长速度一致地形式化为权重距离函数的时间导数,给出梯度Voronoi图的定义。
定义1 普通Voronoi图:设点集P={p1(x1,y1),pn(xn,yn)}⊂ R2,2<n<∞,p为任意一点,p(x,y)∈ R2,存在点pi(xi,yi)与点pj(xj,yj),则称式(1)表达的区域为pi的Voronoi区域:
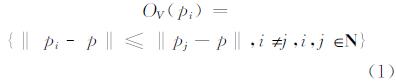
OV={OV(p1),…,OV(pn)}
定义2 权重Voronoi图:设点集P={p1(x1,y1),…,pn(xn,yn)}⊂ R2,2<n<∞,且各点的权值为W={w1,…,wn},wi>0,p为任意一点,p(x,y)∈ R2,存在点pi(xi,yi)与点pj(xj,yj),则称式(2)表达的区域为pi的权重Voronoi区域:
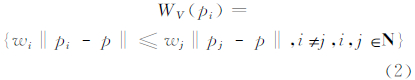
则由点集P的权重Voronoi区域构成的图形称为权重Voronoi图。则由下式表达的图形称为点集P的权重Voronoi图:
WV={WV(p1),…,WV(pn)}
权重是以距离的方式影响生长过程,并最终表现为某一距离条件下相等的边界点,而其位置却是不同的。根据现有文献分析,主要存在基于自权重类型的乘式加权距离(multiplicatively weighted distance,MWD)、基于加权重类型的加式加权距离(additively weighted distance,AWD)、乘方式加权距离(power weighted distance,PWD)以及基于两种类型相结合的组合式加权距离(compound weighted distance,CWD)4种形式[17, 18, 19, 20, 21],它们的公式为:
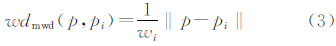
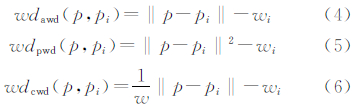
生长元的权重距离取值往往是依据某一属性值直接定值,或是根据几个属性值的计算值定值。就生长元的生长过程来讲,权重距离在生长伊始就已确定,其是一常量,那么表现在单位时间内生长元的生长速度则是恒定的,因此,直接使用权重距离无法动态描述生长元的生长过程。以MWD为例,其生长速度vmwd为:
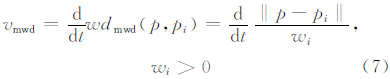
WVD的定义是建立在理想平面之上的,这也验证了上述的分析结果,即WVD是平面光滑、速度恒定的权重Voronoi图。然而,实际应用情况却并非如此理想。一般意义上,地形起伏会诱发出现“顺势”、“逆势”客观条件出现,进而导致生长速度发生非连续性的变化;特殊意义上,空间竞争Voronoi图中,竞争参数会根据时间、位置的变化而变化,其生长速度也是随时间变化的;城市道路Voronoi图中,各路段实际行驶速度不尽相同,同样会导致生长速度变化。为了刻画非理想平面,将上述4种权重值描述为权重距离函数wd(·)形式,使客观条件变化以不同时刻生长速度形式一致性地动态地反映,进而将生长结果表达为生长速度的积分,给出梯度Voronoi图(Gradient Voronoi diagram,GVD)定义。
定义3 梯度Voronoi图:设点集P={p1,…,pn}⊂ R2,2<n<∞,对于任意点pi与pj,存在生长速度pi.v*i与pj.v*j,v*是权重距离函数wd*(·)的时间t导数,则称满足式(8)的区域为pi的梯度Voronoi区域:
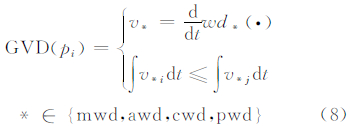
则由点集P的梯度Voronoi区域构成的图形称为梯度Voronoi图:
GVD={GVD(p1),…,GVD(pn)}
2 梯度Voronoi图构建算法定义3表明,生长速度的变化被非理想平面的权重距离函数wd(·)动态描述。wd(·)所能概括的因素条件可分为单因素和多因素两种。对于构建梯度Voronoi图,由于生长过程中存在速度变化,使得几何方式的矢量方法难以表达,而形态学中的膨胀操作算子能够恰当地反映出生长元的变速生长过程,是解决此问题的最佳着眼点。梯度Voronoi图构建算法包括三个关键步聚:① wd(·)权重距离函数,非理想平面建立;② 梯度膨胀过程;③ 膨胀时间收敛,膨胀生长停止条件。以单因素地表高程为例,梯度Voronoi图构建算法如下所述。
2.1 wd(·)权重距离函数格网数字高程模型(grid digital elevation model,GDEM)是以像元值为高程值、实现地形表面离散化表达的一种记录结构。具有像元大小(或分辨率)的属性,而其像元本身存在行(row)、列(column)和高程(elevation)属性,其结构的抽象描述为:
p={grid(row,col,ele),row,col,ele∈ I}
邻域像元之间的数量关系可用像元的高程值表达,以8-邻域膨胀为例,从像元(row,col)=(0,0)开始,邻域像元与当前像元之间的高程差值表达为:
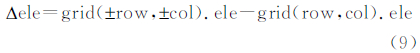
鉴于膨胀方向的可逆性,可将高程差值按照从小到大的顺序排列,如式(10)所示:

此序列为对称序列,根据数量关系对高程差进行分类,0高差表示邻域像元高程值等于当前像元高程值,即“平势”膨胀,生长速度不变;邻域像元高程值小于当前像元高程值为负高差,即“顺势”膨胀,生长速度较“平势”增大;邻域像元高程值大于当前像元高程值为正高差,即“逆势”膨胀方向,生长速度较“平势”减小。序列平移以消除负值,建立如式(11)所示的正高差序列△ELE:
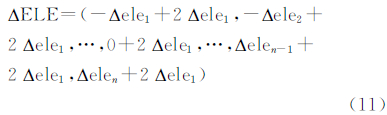
序列值归一化处理,建立加权距离函数wd(·),针对当前像元p及膨胀操作所涉及的像元q,则函数wd(·)可表达为p、q像元之间的高差与序列△ELE总和的比值[22]:
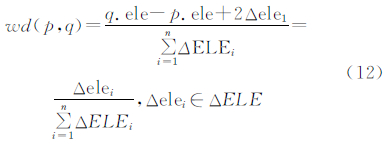
将式(12)代入式(3),得出乘权重距离函数:
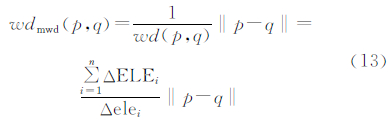
此处,‖p-q‖为GDEM的分辨率值,将其设定为常数c,并将式(13)对时间t求导,得出乘权重距离下的生长速度vmwd:
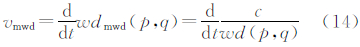
式中,速度是高程差的时间导数,表明膨胀速度(vmvd)是当前像元领域高差和与当前像元、膨胀像元高差的比值,膨胀过程中,其会随着当前像元的改变而变化。
2.2 梯度膨胀过程数学形态学膨胀算子(⊕)描述为[23]:令E=Z2为二维空间欧几里得栅格空间;目标x是E的子集;Q为结构元素;Qs为Q关于原点的对称集合:
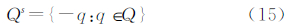
则目标obj的膨胀过程为:
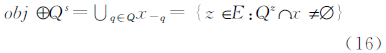
基础像元数据结构描述如下:
Structur edilaPixel
{
integer _ger;
integer _gerFre;
integer _x;
integer _y;
double _frequency;
}
_ger表示当前结构是否为生长元,整数类型,大于0时为生长元及编号,等于0时为非生长元;_gerFre标记当前结构为非生长元结构时的归属,即非生长元被膨胀算子操作后,其所属的生长元势力范围,整数类型;_x、_y用于描述当前结构位置,整数类型;_frequency记录膨胀次数(一般膨胀)或膨胀耗时(变速膨胀),浮点类型。
每次膨胀中每个生长元经过q个影响像元,设生长元的目标数为p,以二维数组pixelSet[p][q]形式存储。以膨胀次数为条件的一般膨胀过程如下:
[1] 第n次遍历生长元集合A;
[2] ∀ai∈A为生长元,二维数组pixelSet[i][]构成n-1次影响像元集E,置临时数组provSet←NULL;
[3] ∀ei∈E,依据式(16)进行1次膨胀,膨胀为集合S;
[4] 如果S=¬Ø,对于∀currPixel∈S,如果currPixel._gor=0 && currPixel._gerFre=0,那么currPixel._frequency←k,currPixel._gerFre←ei._seed,_bDila ←true,provSet←currPixel;
[5] pixelSet[i][]←provSet,i←i+1,转至[2];
[6] 第n次膨胀结束。
2.3 膨胀时间收敛由设定的像元大小(或分辨率)为常数c,得膨胀距离c=vmw·△t仍为一常数。根据式(14)的vmwd与△t互为倒数关系,结合式(12),建立与式(11)相对应的各高程差用时序列△t:
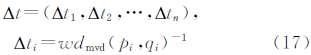
此时,像元之间的膨胀速度不相等,则构建变速膨胀过程以相同的时间消耗为条件。生长元第1次膨胀生长,生长元与其膨胀操作所涉及邻域像元之间存在1∶n关系,若第2次生长,则生长元与其膨胀操作所涉及的领域像元之间存在1∶n∶n2关系,此为迭代过程。如果以树型结构(tree structure)来表达生长元(根结点)在经过多次膨胀操作(中间结点)后到达最终像元(叶结点),那么,用根结点至叶结点的分枝可以表达生长中的非线性对应关系。时间消耗ttotal为:
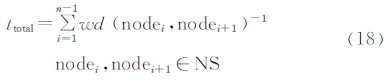
式中,NS(node set)为这条分枝上所经像元组成的中间结点集合。存在膨胀收敛的时间周期t0(∃ti∈△t,t0>ti),则变速膨胀的收敛条件为:
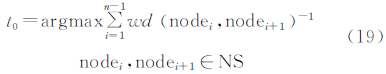
式(19)表示当满足膨胀的时间消耗小于等于t0条件时,该树的分枝上存在的像元个数n的极大值。
结合时间消耗为收敛条件,以基础像元数据结构有相同坐标系与分辨率大小的基底栅格数字高程模型为基础,参照一般膨胀过程,变速膨胀过程描述如下:
[1] t0时间遍历生长元集合A;
[2] ∀ai∈A为生长元,则pixelSet[i][]是前1个时间周期的影响像元集合E,初始化临时像元数组,tempSet←NULL;
[3] ∀ei∈E,依据式(16),膨胀操作1次,得到膨胀邻域集合S;
[4] 如果S=¬Ø,置临时数组tempSet,布尔量_bDila标记发生的有效膨胀,_bDila←false,对于∀currPixel∈S,如果currPixel._gor=0&&currPixel._gorFre=0条件成立;
[4.1] 依据式(12),计算权重DEM(currPixel._x,currPixel._y).ele,DEM(ei.x,ei.y).ele,依据式(18),计算时间消耗ttotal;
[4.2]如果ttotal≤t0,那么currPixel._frequency←ei._frequency+△ele,currPixel._gorFre←ei._gor,tempSet←currPixel,_bDila←true;
[5] 如果_bDila=true,S←tempSet,_bDila←false,转至[4];
[6] 如果_bDila=false,pixelSet[i][]←tempSet,转至[3];
[7] t0时间膨胀结束。
3 算例与分析分析算法各步骤的时间复杂度:设生长元所在的计算域由m行n列像元构成,扫描计算域(m,n),建立wd(·)权重函数,则有Owd(·)(m·n);梯度膨胀过程与一般膨胀过程均是相同范围为计算域,以生长元的膨胀时间收敛为条件,则有Ovdia(c·m·n)。两者相加并化简,得出梯度Voronoi图构建算法的时间复杂度为O(m·n)。
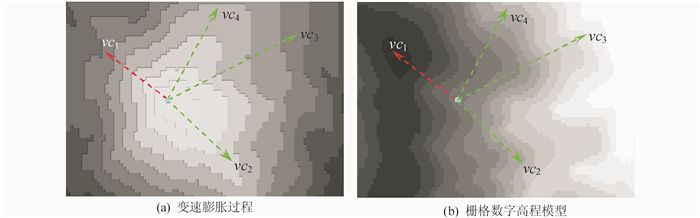
采用云南省昆明市部分1∶2 000比例尺栅格DEM数据为算例,栅格DEM由201行、302列、50×50 m的像元组成,灰度级表示其高程值变化,高程范围在1 570 m(黑)与1 025 m(白)之间,并以分类形式(16类)给出。图 1(a)为某一生长元在10个时间周期的膨胀结果,其中,每一个条带对应一个时间周期;图 1(b)为生长元所存在的基底DEM,一个条带对应一个高程分类。
针对单个生长元情况,为了便于分析,特以生长元为水平位置基准,向周围做出4条辅助向量线(向量vc1~向量vc4)。其中,生长元处于DEM第6分类,vc1由生长元出发并落于高程值最大的第1分类,vc3由生长元出发并落于高程最小的第16分类,并且vc1与vc3具有相同的1~6梯度膨胀时间周期;向量vc2与向量vc4由生长元出发并落于第10分类,但vc2长度小于vc4长度。
分析图 1(a)得出结论,首先,普通Voronoi图栅格算法结果中由膨胀操作会生成以生长元为中心的若干“等距离圆”,而本文梯度Voronoi图算法以时间周期为单位生成若干不规则的封闭“台阶”状条带。其次,在每个时间周期内的变速生长构成了连续有限的空间范围,并且在不同方向上具有较大的差异(台阶边界与生长元距离不同)。算法结果表明在生长过程中生长速度变化和收敛条件均产生了显著影响。
分析图 1(b)得出结论如下。
1) vc1与vc3:二者具有相同的6个膨胀周期,如图 1(b)所示,vc1正高差,逆势、膨胀速度小于正常膨胀速度;vc3负高差,顺势,膨胀速度大于正常膨胀速度。因为vc1方向膨胀速度小于vc3方向膨胀速度,又由于vc1与vc3时间周期相同,可推出vc1方向的膨胀距离小于vc3方向的膨胀距离,与图 1(a)所呈现一致;
2) vc2与vc4:二者存在相同的6分类至10分类高差变化,因为vc2长度小于vc4长度,即vc2方向膨胀速度大于vc4方向膨胀速度,导致在变速膨胀过程中vc2比vc4少用了1个时间周期,与图 1(a)所呈现一致。
|
| 图 1 高程变化的变速膨胀过程 Fig. 1 Progress of Variation Dilation Based on Elevation |
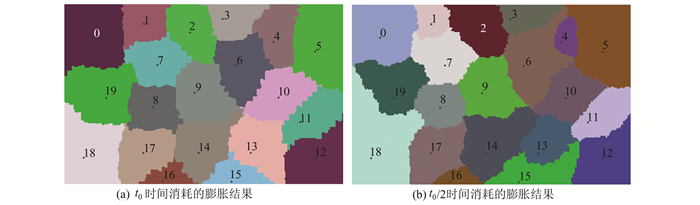
随机产生20个生长元(编号0~19),做不同时间消耗情况下的比较。根据公式(19),设两次时间消耗值分别为t0与t0/2,膨胀结果如图 2所示,分析如下。
|
| 图 2 不同时间消耗的膨胀比较 Fig. 2 Comparison of Dilation Between Different Time Depletions |
1) 时间消耗值为t0情况下,势力范围变化并不明显,表明在时间消耗值较大情况下,虽然各生长元生长速度不同,但经过较长的时间消耗会抵消生长元在生长速度上的差异;
2) 时间消耗值为t0/2情况下,势力范围变化显著,处于正高差的4号、1号与13号生长元生长速度相对较慢,与此相反,处于负高差的6号、2号、15号生长元生长速度较快,在时间消耗值相对较小条件下,使得生长速度差异表现更加明显,有效地反应了地表客观条件变化。
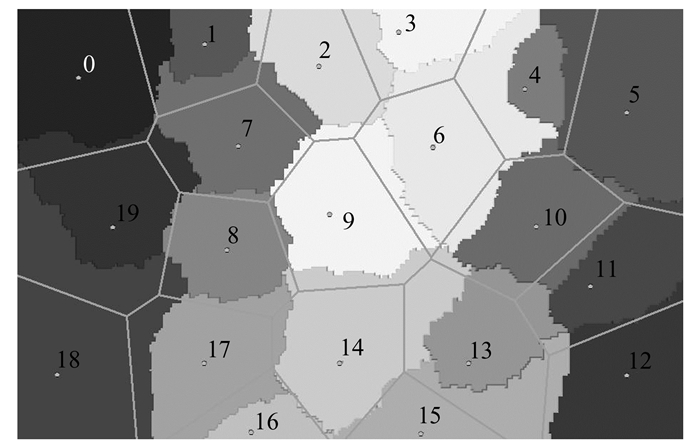
通常普通Voronoi图基于欧式等距离边界生成,其默认所有生长元具有同等影响力;权重Voronoi图基于八邻域膨胀的cost weighted distance累加形式生成,其虽可以反应不同生长元间影响力区别,但生长元自身的影响力是默认无变化的。二者均不能有效地反应生长元自身的影响力变化,都是理想平面生长元匀速生长的结果。本文以生长元生长速度变化为基础构建的梯度Voronoi图,可以客观反应出生长元自身影响力的变化,动态的作用于Voronoi势力范围,生成图形更佳贴合实际。以t0/2时间消耗Voronoi图为基础,如图 3所示,做普通Voronoi图与变速Voronoi图之间图形性质对比分析如下。
|
| 图 3 梯度Voronoi图与普通Voronoi图比较 Fig. 3 Comparison Between GVD and CVD |
(1) 边界的变化。普通Voronoi图中,由于其以理想平面为基础,Voronoi边界由两邻近目标的欧氏距离相等点构成,其表现为一条直线,并且是两邻近目标连线的垂直平分线;而在梯度Voronoi图中,由于其以受到地形影响的各向异性平面为基础,使得生长速度发生变化,表现为梯度Voronoi图边界的不规则与位置偏移。图 3中,梯度Voronoi图边界位置偏移较大的是18与19号生长元,在18至19号生长元方向呈地形下降趋势,使得18号生长速度相对更快,所以,经过相同的生长时间周期后,与普通Voronoi图边界相比,梯度Voronoi图边界更加远离18号生长元,反之同样成立;
(2) 势力范围的变化。由于DEM高程值的作用,存在梯度Voronoi图产生的势力范围与普通Voronoi图所产生的势力范围不一致的情形,即范围的扩大或缩小。1号与4号生长元发生变化明显,它们的梯度Voronoi图势力范围较普通Voronoi图势力范围缩小;5、6、15及18号生长元的势力范围则扩大。变化原因是边界的变化影响导致势力范围变化。势力范围的变化能够反映出自然现象的消长过程;
(3) 邻近关系的变化。10号与14号生长元由普通Voronoi图中的2阶Voronoi邻近关系转变为在梯度Voronoi图中的Voronoi邻近关系,相反情况,3号与4号生长元,它们在普通Voronoi图中为Voronoi邻近关系,而在梯度Voronoi图中,受6号生长元的影响,使它们变为2阶Voronoi邻近关系。邻近关系变化的原因在于势力范围的变化。
4 结 语本文以权重距离函数来描述非理想平面,用权重距离函数的时间导数一致性形式化生长元的变化生长速度,提出了一种新形式Voronoi图——梯度Voronoi图,其在势力范围与Voronoi邻近关系表达方面更具有实际意义。以数学形态学的膨胀操作为基础,通过三个关键步聚,给出了梯度Voronoi图的典型构建算法。算法中,虽然权重距离函数是以单因素DEM高程差为例来确定,但是在连续有界的前提下,通过有效的权重值归一化计算,也同样适用于多因素情况。
值得说明的是,ESRI/ArcGIS/Raster Spatial Analyst/cost weighted distance提供生成代价权重距离方法,可用于代价权重Voronoi图生成。本文算法与其区别如下。
(1) 本文算法以梯度变化所导致的生长元生长速度变化为基础,系列时间周期的生长速度变化使得生长过程是一种动态行为。而代价权重方法每个生长元的cost weighted初始值在生长伊始就已确定,生长过程为匀速,cost weighted难以动态调整;
(2) 本文的核心是以生长速度为基础构建Voronoi图,即d=v×t(距离=速度×时间),如果以八邻域膨胀的cost weighted distance累加形式生长,则生长元的速度不会起到任何作用,即v可以用栅格表达,但在t时间内的最大生长距离需要满足一定的收敛条件,仅仅通过cost weighted distance是不能得出的。
| [1] | Gold C M. Review:Spatial Tessellations-Concepts and Applications of Voronoi Diagrams[J]. International Journal of Geographical Information Science,1994,8(2):237-238 |
| [2] | Chen Jun. Voronoi-based Dynamic Spatial Data Model[M]. Beijing:Publishing House of Surveying and Mapping,2002(陈军. Voronoi动态空间数据模型[M]. 北京:测绘出版社,2002) |
| [3] | Okabe A,Boots B,Sugihara K,et al. Spatial Tessellations:Concepts and Applications of Voronoi Diagrams (2nd Edition)[M]. New York:John Wiley and Sons,2000 |
| [4] | Chen Jun,Li Chengming,Li Zhilin, et al. A Voronoi-Based 9-Intersection Model for Spatial Relations[J]. International Journal of Geographical Information Science,2000,15(3):201-220 |
| [5] | Chen Jun,Zhao Renliang,Li Zhilin. Voronoi-Based K-order Neighbors Relations for Spatial Analysis[J]. ISPRS Journal of Photogrammetric and Remote Sensing,2004,59(1/2):60-72 |
| [6] | Zhao Renliang. Voronoi Methods for Computing Spatial Relations in GIS[M]. Beijing:Publishing House of Surveying and Mapping,2006(赵仁亮. 基于Voronoi图的GIS空间关系计算[M]. 北京:测绘出版社,2006) |
| [7] | Liu Jinyi,Liu Shuang. A Survey on Applications of Voronoi Diagrams[J]. Journal of Engineering Graphics,2004,25(2):125-132(刘金义,刘爽. Voronoi图应用综述[J]. 工程图学学报, 2004,25(2):125-132) |
| [8] | Chen Jun,Zhao Renliang. Spatial Relations in GIS:A Survey on Its Key Issues and Research Progress[J]. Acta Geodaetica et Cartographica Sinica,1999,28(2):97-102(陈军,赵仁亮. GIS空间关系的基本问题与研究进展[J]. 测绘学报,1999,28(2):97-102) |
| [9] | Li Jiatian,Kang Shun,Li Xiaojuan,et al. Putting Model for Broad Geographic Annotation[J]. Geomatics and Information Science of Wuhan University,2015,40(1):20-25(李佳田,康顺,李晓娟,等. 宽泛地理注记的投放模型[J]. 武汉大学学报·信息科学版,2015,40(1):20-25) |
| [10] | Li Jiatian, Kang Shun, Luo Fuli. Point Group Generalization Method Based on Hierarchical Voronoi Diagram[J]. Acta Geodaetica et Cartographica Sinica,2014,43(12):1300-1306(李佳田,康顺,罗富丽. 利用层次Voronoi图进行点群综合[J]. 测绘学报,2014,43(12):1300-1306) |
| [11] | Mostafavi M A,Gold C, Dakowicz M. Delete and Insert Operations in Voronoi/Delaunay Methods and Applications[J]. Computers & Geosciences,2003,29(4):523-530 |
| [12] | Li Chengming,Chen Jun,Li Zhilin. Raster-Based Methods or the Generation of Voronoi Diagrams for Spatial Entities[J]. International Journal of Geographical Information Science,1999,13(3):209-225 |
| [13] | Wang Xinsheng,Liu Jiyuan,Zhuang Dafang,et al. New Raster-Based Method for Constructing Voronoi Diagrams[J]. Journal of China University of Mining & Technology,2003,32(3):293-296(王新生,刘纪远,庄大方,等. 一种新的构建Voronoi图的栅格方法[J]. 中国矿业大学学报,2003,32(3):293-296) |
| [14] | Xie Shunping,Wang Jiecheng,Feng Xuezhi,et al. Algorithm for Constructing Voronoi Diagram of Planar Points Based on Approximating and Extracting Vertices[J]. Acta Geodaetica et Cartographica Sinica,2007,36(4):436-442(谢顺平,王结臣,冯学智,等. 基于结点逼近提取的平面点集Voronoi图构建算法[J]. 测绘学报,2007,36(4):436-442) |
| [15] | Xie Shunping,Feng Xuezhi,Lu Wei. Algorithm for Constructing Voronoi Area Diagram Based on Road Netwrok Analysis[J]. Acta Geodaetica et Cartographica Sinica,2010,39(1):88-94(谢顺平,冯学智,鲁伟. 基于道路网络分析的Voronoi面域图构建算法[J]. 测绘学报,2010,39(1):88-94) |
| [16] | Geng Hong,Tang Xu,Zhu Guorui. Method for Plotting the Affected Area of Urban Roads Based on Spatial Competing[J]. Geomatics and Information Science of Wuhan University,2004,29(6):521-524(耿红,唐旭,祝国瑞. 基于空间竞争的城市道路影响域划分方法研究[J]. 武汉大学学报·信息科学版,2004,29(6):521-524) |
| [17] | Dong Pinliang. Generating and Updating Multiplicatively Weighted Voronoi diagrams for Point, Line and Polygon Features in GIS[J]. Computers & Geosciences,2008,34(4):411-421 |
| [18] | Miller G L,Talmor D,et al. Data Generation for Geometric Algorithms on Non-uniform Distributions[J]. International Journal of Computer Geometry Application,1999,9(6):577-599 |
| [19] | Okabe A,Satohb T,Furutac T,et al. Generalized Network Voronoi Diagrams:Concepts,Computational Methods,and Applications[J]. International Journal of Geographical Information Science,2008,22(9):1-30 |
| [20] | Aurenhammer F,Edelsbrunner H. An Optimal Algorithm for Constructing the Weighted Voronoi Diagram in the Plane[J]. Pattern Recognition,1984,17(2):251-257 |
| [21] | Gahegan M,Lee I. Data Structures and Algorithms to Support Interactive Spatial Analysis Using Dynamic Voronoi Diagrams[J]. Computers, Environment and Urban Systems,2000,24(6):509-537 |
| [22] | Yu Li.Typical Clustering Method Compared Between Distance Proximity and Natural Neighbor[D]. Kunming:Kunming University of Science and Technology,2011(余莉. 距离邻近与自然邻近典型聚类方法比较[D]. 昆明:昆明理工大学,2011) |
| [23] | Rafael C Gonzalez,Richard E Woods. Digital Image Processing (2nd Edition)[M]. Beijing:Publishing House of Electronics Industry,2003 |
 2016, Vol. 41
2016, Vol. 41


