文章信息
- 谭琨, 廖志宏, 杜培军
- TAN Kun, LIAO Zhihong, DU Peijun
- 顾及地面传感器观测数据的遥感影像地面温度反演算法
- Algorithm for Retrieving Surface Temperature Considering HJ-1 Images and Ground Sensor Network Data
- 武汉大学学报·信息科学版, 2016, 41(2): 148-155
- Geomatics and Information Science of Wuhan University, 2016, 41(2): 148-155
- http://dx.doi.org/10.13203/j.whugis20130843
-
文章历史
- 收稿日期: 2014-12-12

2. 南京大学卫星测绘技术与应用国家测绘地理信息局重点实验室, 江苏南京, 210022
2. Key Laboratory for Satellite Mapping Technology and Applications of National Administration of Surveying, Mapping and Geoinformation of China, Nanjing University, Nanjing 210022, China
随着遥感技术的发展以及卫星传感器分辨率的提高,通过遥感方法大范围地对地面定量获取所需参数的应用也越来越广泛。然而,遥感作为一种周期性获取的监测手段,实时性不强,不适合对于热点区域进行实时监控,且由于大气等因素的干扰,整体精度不高。无线传感器网络作为一种地基监测系统,它与遥感数据在功能上形成互补,能够准实时地动态监测区域所需的各种相关参数。宫鹏认为,无线传感器技术是传统遥感技术的新生长点,同时也是遥感、地理信息系统和全球定位系统的延伸[1, 2]。所以融合两者的技术特点,发挥各自的优势,将成为未来发展的趋势。
地表温度的区域分布在气候变化、植被生态、环境监测和城市热岛等研究领域都有着重要的应用价值[3, 4, 5, 6, 7]。地表温度又是地表通量(包括显热、潜热和CO2等通量)、土壤水分含量、作物估产和作物缺水状况监测等遥感模型中的重要输入参数[8]。目前,大范围的地表温度反演主要通过遥感的方法,常用的遥感对地面温度反演算法有单波段的单窗算法、单通道算法[9, 10, 11]和多波段的劈窗算法[12]等。由于地面同步数据的获取以及地表反演温度数据在验证方面的困难,基于地面点数据与遥感数据的协同地表温度反演的研究还比较少。地面无线传感器网络技术的发展使得地面点数据与遥感数据的协同监测成为可能。本文研究了地面点数据与遥感数据在地表温度反演中的协同监测,首先以地面获取的数据值作为地表的真实温度,通过不同的融合方案,建立与遥感数据反演数据的关系模型,然后选择最优的融合方案,该方案可以随着地面数据的不断更新,实现研究区域实时动态的地表温度监测。
1 遥感反演原理及实验融合方案 1.1 基于HJ1B的单窗算法本文采用单窗算法作为遥感反演地表温度的算法,该算法是覃志豪等根据地表热辐射传输方程推导出的一个适合Landsat TM热红外波段反演地表温度的算法[9]。自2008年我国发射环境与灾害监测预报小卫星后,段四波等对该算法进行了改进,使其适合于环境与灾害监测预报卫星B座(HJ1B)的热红外波段。该算法利用地表辐射率、大气水汽含量和地面气温来反演地表温度[13],算法简单易行。其计算公式如下[14]:
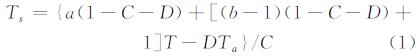
式中,Ts是反演的地表温度;C、D是中间变量,其计算公式为:
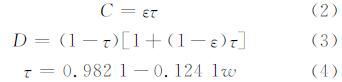
ε为地表比辐射率;τ为大气透射率;本实验采用的水汽含量w由HJ1B CCD影像通过ENVI大气校正FLAASH反演计算得到;a、b是参考系数,当地表温度为0℃~30℃时,a=-60.896 9,b=0.439 078;T为星上亮度温度,有:
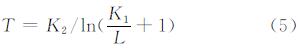
式中,K1、K2为普朗克校正常量,K1=589.33 Wm-2·sr-1·μm-1,K2=1 249.91 K;L为热红外波段的辐射强度(Wm-2·sr-1·μm-1);Ta是大气等效温度,这里采用中纬度冬季模型,有:
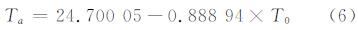
T0为近地层空气温度(K)。
则由式(1)逆运算可得:

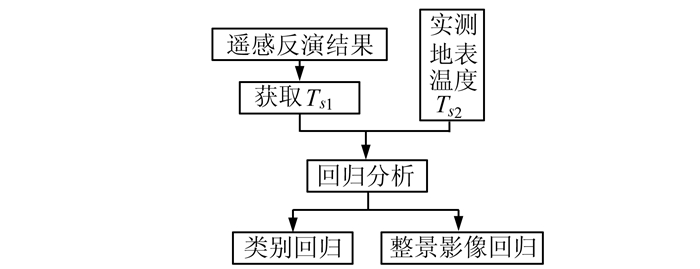
针对地面点数据和遥感数据的特点,提出了两种融合遥感数据与地面实测数据的方法:基于遥感反演结果的融合优化方法和基于反演模型中亮温的融合优化方法。前者直接选用地面实测温度点与相应的遥感反演地表温度结果进行回归分析,原理见图 1。
|
| 图 1 基于遥感反演结果的优化方法 Fig. 1 Optimization Method Based on the Results of Remote Sensing Retrieval |
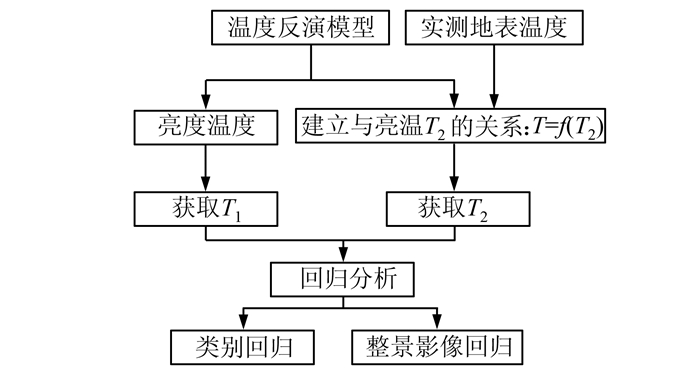
基于反演模型中亮温的融合优化方法,首先对式(1)根据亮温进行逆运算得到式(7),然后把反算的亮温作为星上亮温的真值,与遥感获取的亮温进行回归分析,再选择最优的回归模型对遥感亮温进行修正,最后利用修正的亮温再次通过反演模型重新计算反演的地表温度,见图 2。
|
| 图 2 基于反演模型中亮温的优化方法 Fig. 2 Optimization Method of Brightness Temperature Based on Inversion Model |
该实验选择线性回归、二次方程回归、自然对数方程回归和自然指数方程回归四种回归模型,利用优化后的地表温度与地面数据的相关系数和回归方程的决定系数作为模型评价指标。另外,针对以上两种方法分别运用整景影像的回归优化和按分类类别的回归优化,最终根据以上方法得到四种修正方案,即基于反演结果(方案①)、基于反演结果与类别(方案②)、基于亮温(方案③)和基于亮温与类别(方案④)的方案。基于温度反演结果优化的方案(方案①和方案②)表示采用反演的温度结果与地面传感器所测的温度值直接融合;基于亮温的优化方案(方案③和方案④)采用传感器数据逆运算得到的亮温数据与遥感亮温进行融合;而基于类别优化的方案(方案②和方案④)与基于整体优化的方案(方案①和方案③)的区别在于考虑了地物类别的影响,对不同的地物类别分别进行独立融合分析。最后,对以上四种方案进行评价,得到最优的融合优化模型及方案。
2 数据处理以地面实测的传感器数据为真值,研究地面传感器数据对遥感数据的修正作用,即使得修正后的遥感反演地表温度比未修正的结果更接近于地面实测温度。首先,需要同步获取地面实测数据和遥感数据,但大量的同步地面实测数据的获取非常困难,本文基于两者不同数据的差异性,通过假设具有差异性的反演结果作为地表真实温度,获取其中若干像元点作为地面实测的传感器值。然后,根据这些假设的传感器值来修正遥感反演结果,并分析修正结果的可靠性,最终达到修正结果与假设地面实测数据相逼近的目的。本文选择两景不同时相的HJ1B卫星数据的地表温度反演结果作为研究对象,其中一景作为遥感反演地表温度,另一景作为地表真实温度图,而地面实测数据则从地表真实温度图中选取若干像元值作为地面实测点的地表温度值。
选用2013年1月2日和1月10日徐州市云龙湖附近的HJ1B数据作为遥感反演地面温度的实验数据,该数据的CCD分辨率为30 m,IRS为300 m,实验研究区域见图 3。以2013年1月2日的数据为当日反演数据,1月10日反演的温度图作为地表真实温度图。假定1月10日与1月2日具有相同的反演条件,即两者的地表温度采用1月2日得到的地表比辐射率、地面气温和大气水汽含量。这样处理既可以保证两景数据地表温度反演结果的差异性,同时也可以使得1月10日直接计算的遥感亮温即为假设地面点数据的反算亮温。用假设的像元作为地表实测数据可以避免地面数据点的温度值无法代表混合像元的温度值的问题。首先对这两景数据采用单窗算法反演地表温度,然后提取地表真实温度图中的若干反演温度结果像元作为假设的地面实测点数据,其相应的亮温像元作为反算亮温,通过以上四种方案对1月2日的反演温度结果进行修正,并比较得到最佳的修正方法和回归模型,即得到与地表真实温度图有最高相似度的融合方案,以实现地表温度反演的实时监测。

|
| 图 3 云龙湖附近区域 Fig. 3 Region of Yunlong Lake |
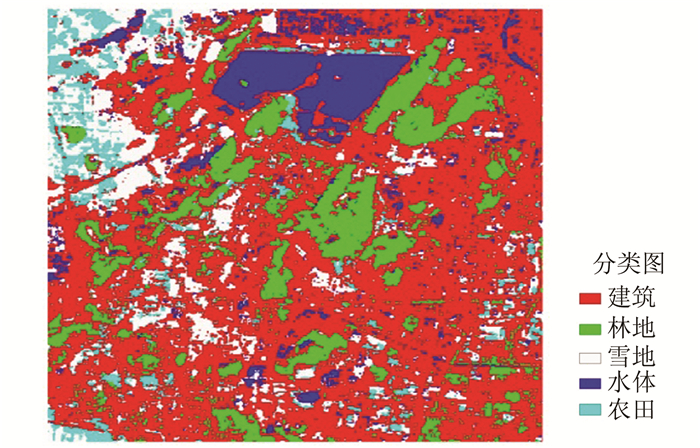
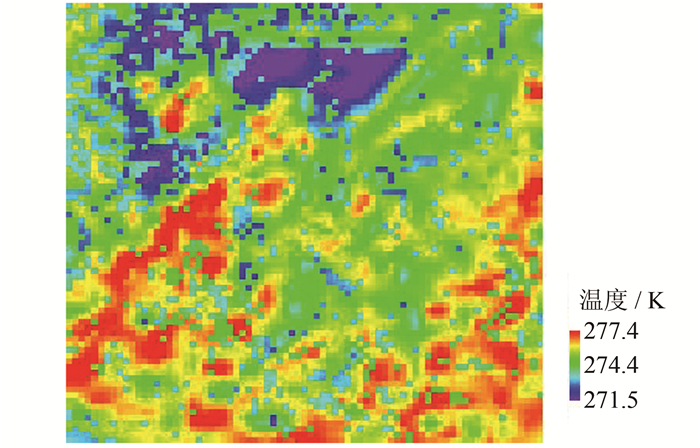
根据1月2日的地面状况,采用支持向量机分类器(support vector machine,SVM)把遥感影像分为建筑、林地、雪地、水体和农田五大类,该分类结果的整体精度为95.1%,见图 4。在热红外数据与多光谱数据的分辨率不一致时,反演时需要把HJ1B数据的分辨率重采样至30 m,本文选用最近邻域法进行重采样。在单窗算法的地表反演中,1月2日的地面气温为-2℃,总水汽含量为0.837 8 g/cm2。由于1月初徐州的雪地覆盖面积变化不大,地表真实温度图由1月10日的遥感数据采用与1月2日相同的反演参数和分类图计算得到。1月2日的温度反演图和地表真实温度图见图 5和图 6,可见,两者地表温度的结果存在一定的差异性。为了获取地面点数据,本文从地表真实温度图中按每间隔2个像元进行取样,获得2 002个像元作为地面实测点,把这些假设的地面实测点和1月2日的遥感数据按照以上四种融合方案进行处理,可以得到修正后的四种反演结果。
|
| 图 4 分类图 Fig. 4 Classification Image |
|
| 图 5 2013年1月2日温度反演图 Fig. 5 Retrieval Image of Land Surface Temperature on January 2,2013 |
|
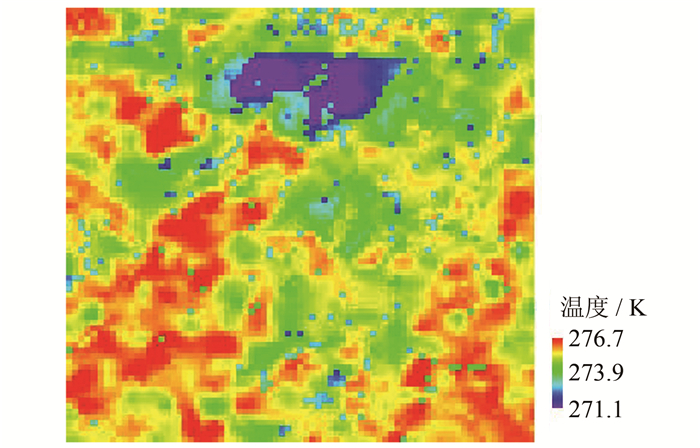
| 图 6 地表真实温度图 Fig. 6 Image of the True Land Surface Temperature |
对得到的遥感影像和假设地面点数据采用四种融合方法进行处理得到的最优回归方程见表 1。四种融合方法显示的结果为从线性回归、二次方程回归、自然对数方程回归和自然指数方程回归中选择出的最优回归方程,即回归方程决定系数最大的结果。在方案①和方案②的回归方程中,x表示原始的遥感影像地表温度数据,y表示融合后的影像的地表温度;方案③和方案④的回归方程中的x和y分别表示遥感数据的原始亮温和融合后的亮温,该亮温通过式(1)可以获得融合后的地表温度。从表 1可以看出,在不同的融合方法中,二次方程回归对地面数据点与遥感数据的融合效果都为最佳。通过最优的回归模型得到四种融合优化后的地表温度图见图 7。
| 融合模型 | 回归方程 | R2 | |
| 方案① | y=-5 382.55+40.723 8x-0.073 3x2 | 0.412 | |
| 方案② | 水体 | y=-9 639.28+71.877x-0.130 3x2 | 0.517 |
| 建筑 | y=3 460.67-23.516 6x-0.043 4x2 | 0.294 | |
| 林地 | y=3 534.99-24.235 8x+0.045 0x2 | 0.417 | |
| 雪地 | y=-4 764.10+36.500 8x-0.066 1x2 | 0.247 | |
| 农田 | y=-10 036.6+74.583 0x-0.134 9x2 | 0.257 | |
| 方案③ | y=-471.896+5.000 1x-0.008 3x2 | 0.347 | |
| 方案④ | 水体 | y=-10 888.4+81.364 3x-0.148 3x2 | 0.507 |
| 建筑 | y=3 724.10-25.720 8x+0.048 0x2 | 0.30 | |
| 林地 | y=4 981.54-35.070 4x+0.065 3x2 | 0.371 | |
| 雪地 | y=-5 381.84+41.193 4x-0.075 0x2 | 0.238 | |
| 农田 | y=-9 310.28+70.022 1x-0.127 9x2 | 0.212 | |
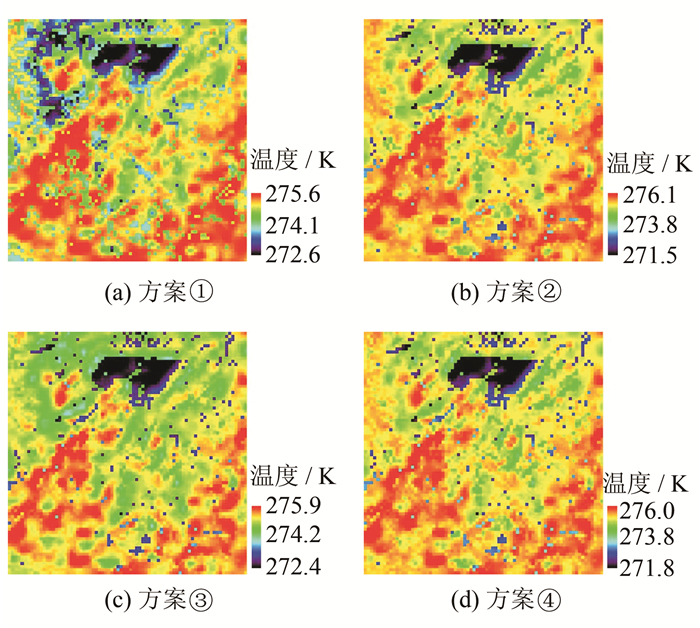
|
| 图 7 四种融合优化结果 Fig. 7 Four Results of Fusion Optimization |
原始的遥感地表温度图(图 5)中的西北方位与假设的地表温度图(图 6)相比有明显的低温区域,把融合优化后得到的四种结果图与假设的地表温度图进行对比可以看出,基于反演结果的融合方案在该区域变化不明显,其余三种融合优化的结果都有明显的变化。从整体影像上的数据统计分析(表 2)可以看出,四种方案回归后,均值都更加接近于假设的真值,但是标准差变小。基于整体影像的优化方案结果的离散程度变化明显,即最小值、最大值偏差较大,标准差相对变小,与假设地表温度图的偏差较大;基于分类的优化方案的分布调整较好,与假设情况比较贴近。
| 统计结果 | 最小值/℃ | 最大值/℃ | 均值/℃ | 标准差 |
| 地表真实温度图 | 271.138 2 | 276.665 9 | 274.889 2 | 0.848 5 |
| 遥感反演温度 | 271.540 0 | 277.356 3 | 274.964 7 | 1.103 2 |
| 方案① | 272.642 1 | 275.566 4 | 274.875 2 | 0.548 9 |
| 方案② | 272.407 9 | 275.942 6 | 274.884 8 | 0.640 0 |
| 方案③ | 271.538 1 | 276.051 8 | 274.889 0 | 0.730 2 |
| 方案④ | 271.560 1 | 276.039 7 | 274.891 4 | 0.728 9 |
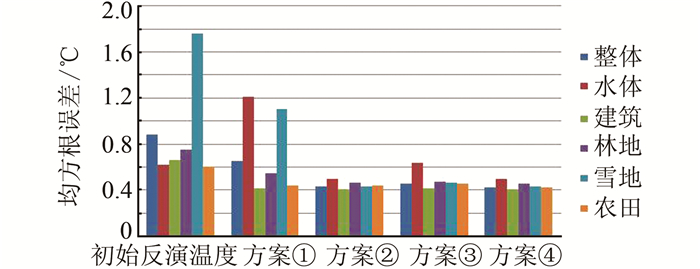
对四种融合优化结果分别与地表真实温度图进行误差分析,得到的原始的遥感反演的地表温度以及各优化结果与假设地面温度的均方根误差见图 8。从图 8中可以看出,通过各种方案的优化,除方案①中水体的均方根误差变大外,四种优化修正温度图的均方根误差都变小。基于分类的优化方案明显要优于基于整体影像的优化方案;基于亮温的优化方案效果要优于基于温度反演结果优化的方案。基于亮温与类别(方案④)进行回归优化的结果的均方根误差最小,效果最优。
|
| 图 8 实验1均方根误差比较 Fig. 8 Comparison of RMS Errors in Experiment 1 |
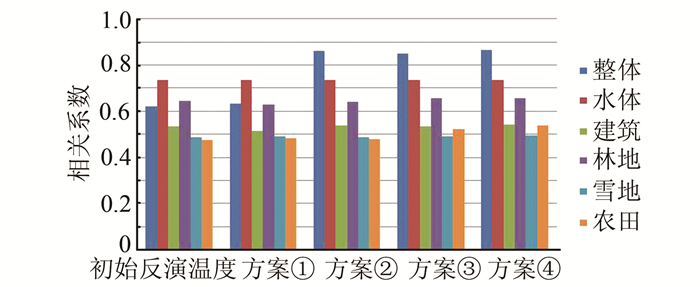
相关系数表示两影像中相应像元之间的相关程度,本文计算的假设地表温度图与各优化修正结果的相关系数见图 9。从图 9中可知,经过优化方案得到的优化结果都要比初始反演的温度图的相关系数高,且基于分类的优化方案高于基于整体的优化方案。基于亮温与类别(方案④)的相关系数最高。
|
| 图 9 实验1相关系数的比较 Fig. 9 Comparison of Correlation Coefficients in Experiment 1 |
实验的原理主要是通过假设地表温度图的像元来代表每个地面点获取的值,各方案的优化结果与像元的分辨率无关,它与采样的间隔像元数相关。为了获取取样间隔大小与回归优化效果的关系,本文对1月2日的数据分别从间隔0~15个像元进行采样,得到以上四种优化方案的地表温度融合结果,并把所得到的结果分别采用相关系数和均方根误差进行评价。
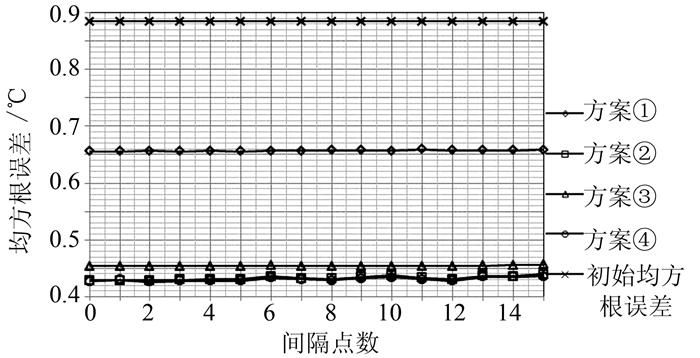
从图 10显示的各方案结果的均方根误差变化情况可以看出,四种方案的均方根误差相对于初始反演影像都变小。基于亮温的优化方案的均方根误差要小于基于遥感反演结果的优化方案,基于类别的优化结果的均方根误差要小于基于整体的优化方案。间隔点数越大,回归分析的点数越少,各种优化方案的均方根误差都在不断变大,但是变化的幅度不大。
|
| 图 10 均方根误差变化比较 Fig. 10 Comparison of the Change of RMS Errors |
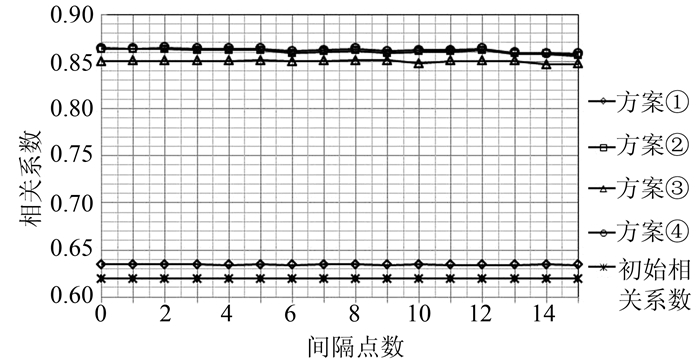
从图 11的相关系数变化可以看出,通过四种方案优化后的结果相对于初始反演结果的相关性要好。从基于亮温的优化方案得到的相关系数要大于基于反演温度优化的方案,基于类别的优化结果大于基于整体的优化结果。基于反演结果与类别的方案(方案②)和基于亮温与类别的方案(方案④)效果较好,但方案④的效果最优。各种优化方案的相关系数随取样点数的减少而不断变大,但是变化的幅度不大。
|
| 图 11 相关系数变化比较 Fig. 11 Comparison of the Change of Correlation Coefficients |
为了验证融合方案的有效性,采用2013年1月14日的数据代替2013年1月10日的数据,作为1月2日的假设地表真实温度,然后进行类似处理,把假设地表温度影像按间隔2个像元进行采样的2 002个像元作为地面传感器获取的温度值。
3.4.1 建立回归模型通过四种模型回归获得最佳回归方程,表 3为得到的最大决定系数和相应的回归方程。可以看出,1月14日的数据和1月2日的数据差异比较大,各回归方程的决定系数都不大。除方案②的融合模型水体的假设地面地表温度与遥感结果拟合的方程为自然对数函数,其余的拟合结果都为一元二次方程。
| 融合模型 | 回归方程 | R2 | |
| 方案① | y=-195 96.8+144.833x-0.263 9x2 | 0.278 | |
| 方案② | 水体 | y=e0.000 98x+5.341 7 | 0.109 |
| 建筑 | y=-998.427+9.369 1x-0.017 4x2 | 0.092 | |
| 林地 | y=2 059.08-12.784 7x-0.022 90x2 | 0.088 | |
| 雪地 | y=-716 8.34+54.479 8x-0.099 7x2 | 0.059 | |
| 农田 | y=-3 469.83+27.448 8x-0.050 3x2 | 0.009 | |
| 方案③ | y=3 189.92-21.351 2x+0.039 06x2 | 0.048 | |
| 方案④ | 水体 | y=-1 059.62+9.529 5x-0.017 0x2 | 0.109 |
| 建筑 | y=-1 820.42+15.576x-0.029 0x2 | 0.103 | |
| 林地 | y=4 255.26-29.089 3x+0.053 1x2 | 0.109 | |
| 雪地 | y=-7 610.52+58.297 1x-0.107 8x2 | 0.078 | |
| 农田 | y=-1 987.59-12.527 7x+0.022 9x2 | 0.033 | |
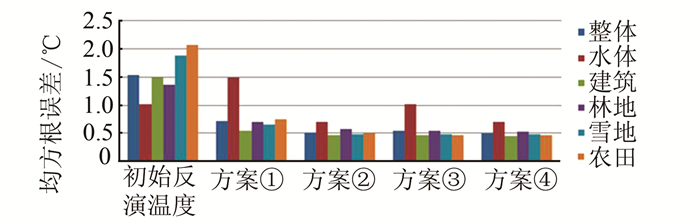
从图 12中可以看出,直接基于反演结果的方案①的效果不稳定,水体的均方根误差反而偏大,其余各修正温度图的均方根误差都变小。基于类别的方案②和方案④进行回归得到的结果明显要优于按整体进行回归的方案①和方案③得到的结果,方案④的各项均方根误差都最小。
|
| 图 12 实验2均方根误差比较 Fig. 12 Comparison of RMS Errors in Experiment 2 |
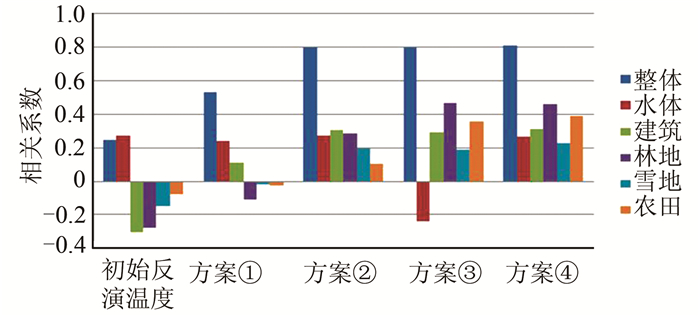
从图 13可知,经过优化的整体的相关系数都比较高,但是未经过类别优化的方案①和方案③的部分类别,如水体和建筑的相关系数反而变小了;基于类别的方案②和方案④高于基于整体的方案①和方案③的相关系数,方案④的相关系数最高,与之前的结果相符。
|
| 图 13 实验2相关系数的比较 Fig. 13 Comparison of Correlation Coefficients in Experiment 2 |
为了进一步验证融合算法的有效性,在2013年1月10日当天布设了若干地面无线传感器与环境卫星过境进行同步观测,利用地面无线传感器获得的真实地表温度与融合优化结果进行相对精度评价。首先选取云龙湖附近不同类别的区域,针对不同地物布设6个地面传感器节点,地面无线传感器见图 14。根据遥感影像过境的时间获取各点的地表温度值,然后与以上融合方法的相应像元值进行对比,如表 4所示。

|
| 图 14 地面无线传感器 Fig. 14 Ground Wireless Sensor |
由于地表真实温度图是由2013年1月10日过境的环境卫星数据反演得到的,且采用1月2日的反演参数,与1月10日实际的地面无线传感器实测的数据有必然的偏差,其均方根误差为2.612℃,而1月2日的遥感反演结果与地面无线传感器实测值的偏差更大,其均方根误差为3.663℃。从表 4可知,通过四种融合方案的遥感反演修正结果与实测地面无线传感器的均方根误差都相应变小,且更接近于假设地表温度与实测数据的均方根误差。另外,与其他三种融合方法相比,方案④所得到的结果与地面传感器实测的误差最小,其均方根误差为2.646℃,这与地表真实温度图的均方根误差最为接近。
| 点号 | 类型 | 实测温度值 | 地表真实温度图像元值 | 1月2日反演的温度值 | 方案① | 方案② | 方案③ | 方案④ |
| 1 | 水体 | -2.6 | 0.545 | 1.964 | -0.777 | -0.933 | 1.835 | 1.662 |
| 2 | 水体 | 3.1 | 2.663 | 0.02 | -0.214 | 1.937 | -1.143 | -0.46 |
| 3 | 水体 | -2.2 | 0.066 | 1.876 | 1.298 | 1.388 | -0.918 | -1.054 |
| 4 | 建筑 | -0.9 | -0.236 | 0.335 | 0.718 | 0.308 | -1.573 | -1.633 |
| 5 | 林地 | 0.15 | -0.286 | 1.724 | 1.230 | 1.237 | -0.918 | -0.054 |
| 6 | 雪地 | -2.7 | 1.575 | 1.321 | 1.232 | 1.639 | -1.307 | -1.192 |
| 均方根误差 | 2.612 | 3.663 | 3.026 | 2.774 | 2.927 | 2.646 | ||
以上实验表明,通过建立合适的数据融合优化模型,采用地面数据点可以对遥感反演的地表温度结果进行修正,并提高反演的精度。实验结果与分析表明,通过四种方案的融合优化,融合后结果的均方根误差分别从0.884 8℃下降为0.656 2℃、0.428 8℃、0.453 5℃、0.426 1℃;相关系数从初始的0.619 5分别提高到0.634 3、0.862 9、0.850 7、0.864 8,这表明方案④的融合效果最好。整体上,该方案随不同的间隔变化,均方根误差能够保持在0.45℃以下。修正结果与假设地面值的相关系数保持在0.85以上,且在该方案中,整体的温度值的分布情况与假设地表温度值最接近。
| [1] | Gong Peng. Wireless Sensor Network as a New Ground Remote Sensing Technology for Environmental Monitoring[J]. Journal of Remote Sensing, 2007,11(4):545-551(宫鹏.环境监测中无线传感器网络地面遥感新技术[J]. 遥感学报, 2007,11(4):545-551) |
| [2] | Gong Peng. Progress in Recent Environmental Applications of Wireless Sensor Networks[J]. Journal of Remote Sensing, 2010, 14(2):387-395(宫鹏.无线传感器网络技术环境应用进展[J]. 遥感学报, 2010,14(2):387-395) |
| [3] | Li Dongliang, Guo Hui, Li Yueqing, et al. Prediction of 0 cm Average Ground Surface Temperature Changes along Qinhai-Xizang Railway[J]. Plateau Meteorology, 2005, 24(5):685-693(李栋梁,郭慧,李跃清,等.青藏高原及铁路沿线地表温度变化趋势预测[J].高原气象,2005,24(5):685-693) |
| [4] | Gong Zhiqiang, Wang Xiaojuan, Zhi Rong, et al. Regional Characteristics of Temperature Changes in China During the Past 58 Years and Its Probable Correlation with Abrupt Temperature Change[J]. Acta Physica Sinica, 2009,58(6):4342-4353(龚志强,王晓娟,支蓉,等.中国近58年温度极端事件的区域特征及其与气候突变的联系[J].物理学报,2009,58(6):4342-4353) |
| [5] | Li Baofu, Chen Yaning, Shi Xun, et al. Temperature and Precipitation Changes in Different Environments in the Arid Region of Northwest China[J].Theoretical and Applied Climatology, 2013, 112(3/4):589-596 |
| [6] | Tan C L, Wong N H, Jusuf S K. Outdoor Mean Radiant Temperature Estimation in the Tropical Urban Environment[J]. Building and Environment, 2013, 64(6):118-129 |
| [7] | Zhang Yong, Yu Tao,Gu Xingfa,et al. Land Surface Temperature Retrieval from CBERS-02 IRMSS Thermal Infrared Data and Its Applications in Quantitative Analysis of Urban Heat Island Effect[J]. Journal of Remote Sensing, 2006,10(5):789-797(张勇,余涛,顾行发,等. CBERS-02 IRMSS热红外数据地表温度反演及其在城市热岛效应定量化分析中的应用[J].遥感学报,2006,10(5):789-797) |
| [8] | Huang Miaofen, Xing Xufeng, Wang Peijuan, et al. Comparison Between Three Different Methods of Retrieving Surface Temperature from Landsat TM Thermal Infrared Band[J]. Arid Land Geography, 2006,29(1):132-137(黄妙芬,刑旭峰,王培娟,等.利用Landsat/TM热红外通道反演地表温度的三种方法比较[J].干旱区地理, 2006,29(1):132-137) |
| [9] | Qin Zhihao, Karnieli A. A Mono-window Algorithm for Retrieving Land Surface Temperature from Landsat TM Data and Its Application to the Israel-Egypt Border Region[J]. International Journal of Remote Sensing, 2001,22(18):3719-3746 |
| [10] | Jiménez-Muoz C, Cristóbal J, Sobrino J,et al. Revision of the Single-Channel Algorithm for Land Surface Temperature Retrieval from Landsat Thermal-Infrared Data[J]. IEEE Transactions on Geoscience and Remote Sensing,2009,47(1):339-349 |
| [11] | Weng Q, Lu D, Schubring J. Estimation of Land Surface Temperature-Vegetation Abundance Relationship for Urban Heat Island Studies[J]. Remote Sensing of Environment, 2004,89(4):467-483 |
| [12] | Mao Kebiao, Qin Zhihao, Shi Jiancheng, et al. The Research of Split Window Algorithm on MODIS[J]. Geomatics and Information Science of Wuhan University, 2005,30(8):703-707(毛克彪,覃志豪,施建成,等.针对MODIS影像的劈窗算法研究[J].武汉大学学报\5信息科学版,2005,30(8):703-707) |
| [13] | Qin Zhihao, Li Wenjuan, Zhang Minghua, et al. Estimating of the Essential Atmospheric Parameters of Mono-Window Algorithm for Land Surface Temperature Retrieval from Landsat TM6[J]. Remote Sensing for Land & Resources, 2003,56(2):37-43(覃志豪, Li Wenjuan, Zhang Minghua,等.单窗算法的大气参数估计方法[J].国土资源遥感.2003,56(2):37-43) |
| [14] | Duan Sibo,Yan Guangjian, Qian Yonggang. et al.Two Single-channel Algorithms for Retrieving Land Surface Temperature from the Simulated HJ-1B Data[J]. Progress in Natural Science, 2008, 18(9):1001-1008(段四波,阎广建,钱永刚,等.利用HJ-1B模拟数据反演地表温度的两种通道算法[J].自然科学进展,2008,18(9):1001-1008) |
 2016, Vol. 41
2016, Vol. 41


