文章信息
- 刘经南, 张化疑, 刘焱雄, 陈武, 周兴华
- LIU Jingnan, ZHANG Huayi, LIU Yanxiong, CHEN Wu, ZHOU Xinghua
- GNSS研究海潮负荷效应进展
- Progress of Ocean Tide Loading Inversion Based on GNSS
- 武汉大学学报·信息科学版, 2016, 41(1): 9-14
- Geomatics and Information Science of Wuhan University, 2016, 41(1): 9-14
- http://dx.doi.org/10.13203/j.whugis20150621
-
文章历史
- 收稿日期: 2015-10-13

2. 国家海洋局第一海洋研究所, 山东 青岛, 266061;
3. 香港理工大学, 香港 红磡
2. The First Institute of Oceanography, SOA, Qingdao 266061, China;
3. The Hong Kong Polytechnic University, Hung Hom, Hong Kong, China
日月对地球的引潮力作用,不仅使固体地球产生周期性的形变(固体潮),而且使海水产生周期性变化(海洋潮汐)。同样,海洋潮汐引起的海水质量重新分布也会使固体地球产生周期性的形变,这一形变通常称之为海潮负荷效应。研究表明,海潮负荷效应包括:(1)在海洋潮汐作用下产生的地壳变形; (2)海水的直接引力;(3)上述变形使得质量重新分布而产生的附加位[1]。
随着科技的进步,观测仪器精度的提高,海潮负荷效应在全球导航卫星系统(global navigation satellite system,GNSS)大地测量、海洋动力学以及地球物理、地球动力学研究中的应用越来越广泛,对其精度的要求也越来越高。在沿海地区,海潮负荷效应引起的形变可达数厘米。因此,在GNSS高精度数据处理过程中都必须消除海潮负荷的影响[2]。其次,海潮负荷是海洋动力学模拟中必须考虑的因素,是海洋动力学研究的实际或急迫需求。另外,利用地表重力场观测精密测定地球潮汐常数,反演研究地壳上地幔构造、地球内核运动、地球近周日自由摆动和极移重力效应方面的问题时,必须考虑到海潮负荷效应的影响[3]。此外,海潮负荷引起地球物理场的变化还会引起低轨卫星轨道的摄动[1],随着对低轨卫星定轨精度的要求越来越高,海潮负荷也会受到越来越多的关注。
本文中关于GNSS研究海潮负荷效应进展的介绍,主要针对由海洋潮汐引起的地壳几何变形展开。
1 海潮负荷效应研究方法海潮负荷现象引起地面测站位置周期性形变,一般来说越靠近沿海地区影响越大[4]。由于固体潮和海潮都是日月引潮力作用的结果,而海潮负荷又是海潮对固体地球的影响,因此,海潮负荷、固体潮以及海潮的频率特征相同,利用通用的滤波方法很难将海洋负荷的影响从固体潮观测资料中分离出来,只能采用其他办法。
文献[5]提出海潮负荷(包括位移、重力、倾斜、应变等)可以由海潮模型和基于地球模型的格林函数(对应位移、重力、倾斜、应变等)通过离散褶积积分求得。
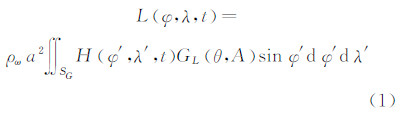
其中,φ和λ分别是计算点的经度和纬度;φ′和λ′分别是负荷点的经度和纬度;a是地球半径;ρω是海水密度;L(φ,λ,t)是海潮负荷;H(φ′,λ′,t)是全球区域SG中负荷点处第i个分潮的瞬时潮高,用复数表示;A是计算点到负荷点的方位角;θ是计算点(φ,λ)到负荷点(φ′,λ′)的球面距离;GL(θ,A)是质量负荷格林函数。
从式(1)中可以看出,海潮负荷L(φ,λ,t)的精度主要由海潮模型H(φ′,λ′,t)、格林函数GL(θ,A) 以及负荷积分计算方法等因素有关。相关研究表明,海洋负荷潮汐对格林函数和积分方法不敏感,采用不同的格林函数对海洋负荷潮汐的影响小于2%[6],而采用不同的积分方法对其影响为2%~5%[7, 8]。因此,海潮负荷的精度主要取决于海潮模型的精度。超导重力仪测量和甚长基线干涉测量(very long baseline interferometry,VLBI)在研究海洋负荷效应方面具有精确可靠的优势[9, 10, 11, 12],但 由于观测设备昂贵,不适宜大规模建站,因而限制了其在海洋负荷潮汐研究中的应用。
近十几年来,由于GNSS(当前主要还是GPS)高精度定位应用的需要,研究人员发现海潮引起的海水质量重新分布使得沿海地区GNSS站址位置发生周期性变化,大小约为1~2 cm,而在法国西北部地区高达16 cm[13, 14]。在高精度GNSS数据处理中,必须将海潮引起的这种周期性变化消除掉(尤其是在沿海地区)。反而言之,沿海GNSS观测值对海洋潮汐响应灵敏,也可以通过GNSS观测值准确地获取这些海潮负荷引起的观测“偏差”。文献[15, 16]研究表明,利用GNSS测定海潮负荷位移参数的精度可与VLBI相提并论。 而且,GNSS相比重力测量和VLBI具有测站多、覆盖广、成本低廉、全天候观测的优势,但目前GNSS自身还存在系统误差(主要是轨道误差)和偶然误差,因此在研究海潮负荷时还存在许多问题[17]。
2 当前GNSS研究海潮负荷效应进展GNSS精密定位与海潮负荷的关系有两种研究方向。一种是以“提高定位精度”为目的,引入海潮模型,然后基于海潮负荷理论公式求得海潮负荷位移;另一种是以“获取海潮负荷信息”为目的,利用GNSS长期观测结果获取海洋负荷潮汐的特征信息,然后通过数据分析(频谱分析或者卡尔曼滤波)以及模型构建,得到不同地区的海潮负荷位移模型。
2.1 海潮负荷位移模型海潮负荷位移计算的实质是通过式(1)积分在频域中求出各测站处每个分潮的振幅和相位,因此,总的海潮负荷位移就是不同潮波的叠加。
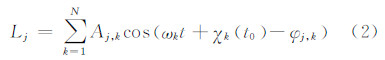
Lj(j=1,2,3)分别为海潮负荷对测站东、北和垂直方向的瞬时位移分量;N为叠加的分潮数;ωk、χk(t0)分别为各分潮角频率和天文幅角初相;Aj,k、φj,k分别为k分潮在j方向上的振幅和格林尼治相位。根据国际地球自转服务(International Earth Rotation Service,IERS)规范,一般主要考虑11个主要分潮的影响(4个周日分潮K1、O1、P1、Q1,4个半日分潮M2、S2、N2、K2,还有3个长周期分潮Mm、Mf和Ssa)。
在利用GNSS反演海潮负荷位移时,为了方便对海潮负荷位移参数建模,需要将式(2)线性化。长周期项的影响很小,忽略3个长周期潮波,式(2)可改写为:
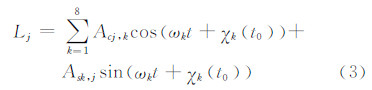
其中
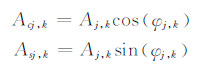
Acj,k和Asj,k作为未知数,每个分潮有6个未知参数,这样,每个测站就需要估计48个海潮负荷位移参数。
2.2 利用海潮负荷位移模型提高GNSS定位精度的研究20世纪90年代以来,国外相关研究人员主要集中在实用性、不同海潮模型及其比较和浅水效应3个方面对海潮负荷位移模型进行研究,用以提高定位精度。
1) 实用性研究。文献[18, 19, 20, 21, 22, 23]的研究表明,通过改正海潮负荷位移能够提高GNSS的最终定位精度,IERS也明确推荐了海潮负荷位移改正方法[24]。国外知名GNSS精密定位定轨软件(如GAMIT、BERNESE、GIPSY等)中也增加了海潮负荷位移改正,不但可以提高GNSS精密定位和定轨的精度,同时也可以提高天顶对流层延迟以及大气可降水汽量的估算精度[25]。
2) 海潮模型及其比较研究。自1994年以来,陆续有20多个全球海潮模型GOT00.2、TPXO.2、TPXO.6、FES95.2、FES99、CRS3、CRS4、OSO 和NAO.99b 等)[26, 27, 28]对外发布,精度提高到几厘米,分辨率也提高到0.125°×0.125°。文献[29]利用分布全球的140个IGS站对FES95.2、FES99 和GOT00.2模型的精度进行评价,发现这三个模型与GNSS估算的结果总体来说一致性非常好。LFG/OLMPP、 SPOTL和CARGA是国际上计算海潮负荷位移的主流软件,文献[28]利用LFG/OLMPP 软件计算沿海区域海潮负荷位移时,采用不同的海潮模型得到的结果相差达到20%,利用双线性内插提高浅水区域分辨率后,三种软件采用相同的海潮模型计算的结果差异仅为毫米级。
3) 浅水效应研究。海潮负荷位移模型的精度主要取决于海潮模型的精度,近海潮汐受海岸线及海底地形的影响较大,尤其在海湾、海沟及浅海,由于水深资料、底摩擦系数和黏性系数的不确定性,海潮模型在浅水区域的精度仍然欠佳。文献[26]发现不同的海潮模型在深海海域同一地点的潮位相差仅为2~3 cm,但在浅海海域相同位置模型之间的潮位预报结果差异较大;上述海潮模型都是基于卫星测高数据或者同化卫星测高数据而构建的,近岸地区海洋环境较为复杂,且雷达回波受到陆地反射信号的干扰,卫星测高数据质量差,导致海潮模型在浅水区域精度欠佳。现有的技术手段(卫星测高回波波形重跟踪方法)还不能从根本上解决卫星测高在浅水海域精度较低的问题[30]。日本国立天文台(NAOJ)发布的NAO.99Jb模型由于采用Blending方法同化了TOPEX/ POSEIDON 测高卫星数据和日本、韩国沿岸219个验潮站的资料,使得该模型在日本周边浅水区域的共线残差小于其他海洋潮汐模型[31]。文献[32]指出NAO.99Jb模型相比其他模型更适用于朝鲜半岛。文献[22]发现FES2004 模型中的M2不适用于法国的西北部,原因是在St-Malo区域,潮差最大超过14 m,潮位变化产生的能量非常大,属于高能浅水区,受此以及半日和更高频率潮汐非线性相互作用的共同影响,海潮模型的振幅和相位与实际偏差较大。
国内研究人员也围绕“提高定位精度”方向开展了许多研究工作。文献[33]对海洋负荷潮汐对测站位移的影响进行研究,在推导过程中回避了将点负荷密度展开为球谐函数不收敛的问题。文献[13]研究了瑞典OSO天文台和日本国家天文台所发布的海洋负荷改正模型对GNSS精密定位的影响,在大洋和内陆,两者结果的差异较小,但在沿海地区差异较大。即使采用相同的潮波数目,在上海地区,OSO和NAOJ发布的模型差值达到8.2 mm。文献[34]利用TPXO.6海潮模型和中国东海和南海潮汐资料研究了海潮负荷对我国沿海部分台站负荷位移的影响,发现沿海地区海潮负荷位移水平和垂直分量均达到了毫米级,其中厦门站水平分量和垂直分量的振幅分别接近3 mm和15 mm。另外,由于全球海潮模型在近海区域不精确,导致海潮负荷位移在沿海区域精度不高,有必要采用高精度的近海潮汐资料替代海潮模型计算海潮负荷位移。
上述国内外研究人员的研究证明了海潮负荷位移改正对于提高GNSS定位精度具有非常重要的作用。但是,由于浅水效应的存在以及验潮资料的缺失,海潮模型在浅水区域的精度不高,导致沿海地区海潮负荷位移模型的精度还不能满足IERS 规范所要求的精度。因此,如何提高沿海地区海潮负荷位移模型的精度也是研究人员关注的重点和难点。
2.3 利用GNSS获取海潮负荷位移模型的研究近几年,国外学者尝试利用大地测量的方法获取海潮负荷位移模型,取得了一些新进展。
极地是利用卫星测量研究地壳运动、冰后回弹、冰盖物质平衡等的代表性区域,文献[27, 35]采用GNSS和重力数据评估了南极地区的海潮负荷模型,发现利用TPXO.6、CADA00.10、FES99和CATS02.01等最新的模型,整体符合都比较好。其中,利用GNSS对比海潮负荷位移时,N2和Q1分潮符合最好,K2和K1分潮较差,其原因可能是GNSS轨道和星座重复周期分别与这两个分潮的周期相重合导致的估计误差。文献[36]将GRACE结果与欧洲IGS站3 a的高程残差进行比较,发现内陆的IGS站与GRACE结果一致性比较好,沿海的IGS站与GRACE结果差异比较大,其原因是在GNSS数据处理过程中,半日海潮负荷位移改正残差引起了伪周年变化。文献[37]利用英国GNSS观测数据研究海潮负荷位移时发现,GNSS得到的半日潮结果(S2 和M2 )与FES99 模型结果仅仅相差5%。但是与TPXO.2 模型结果的差值达到20%,尤其对周日分潮(K1和P1)来说,差值更大。文献[14]利用法国西北部的Brittany和Cotentin地区(该地区潮差达14 m,是欧洲潮差最大的地区)14 个GNSS观测站2004年105 d数据的分析结果发现,GNSS反演的海潮负荷位移与FES2004模型的振幅有2~7 mm的差异。其中,M2、N2、O1、Q1四个分潮相差在亚毫米量级,而S2和K1与FES2004模型的差异在毫米量级。
国内在利用GNSS“获取海潮负荷”方面的研究较少,文献[2, 38]研究结果表明,在香港地区周日分潮O1、P1、Q1和半周日分潮M2、N2与GOT 4.7及NAO.99b 模型的残差都在亚毫米量级。而S2、K1、K2 与模型相差较大,由于所采用的数据主要在香港地区,成果的代表性也需要进一步 研究。文献[39]利用1996~2011年全球456个GNSS长期观测站的观测数据解算8个主要海潮分量的负荷位移,发现M2、N2、O1和Q1 4个纯太阴分潮引起的潮汐负荷位移,在水平方向上的精度为0.12 mm,在垂直方向上的精度为 0.24 mm,而S2、K2、K1和P1与太阳相关的分潮精度稍低,该精度已优于现有的固体潮汐模型和海潮负荷位移模型的精度。另外还发现,在全球范围(除某些沿海地区外)最新的海潮负荷位移模型(FES2004,TPXO.7.2,HAMTIDE11a,DTU10,EOT11a和GOT4.7)与GNSS解算结果符合较好。该研究利用了全球的GNSS观测数据,并通过改进模糊度解算方法提高了海潮负荷位移模型的解算精度,因此研究成果更具有代表性,也充分说明了利用GNSS可以获取高精度的海潮 负荷位移模型。
利用GNSS长期观测结果获取海洋负荷潮汐的特征信息,然后通过数据分析以及模型构建,得到不同地区的海潮负荷位移模型,有效避免了浅水效应的影响,并且具有测站多、覆盖广、成本低廉、全天候观测的优势。研究人员在利用GNSS技术获取海潮负荷位移模型时,主要采用单天解的方式,从坐标分量的时间序列中分离出各主要海潮分量的负荷效应,或者直接以未知数的方式由单天解计算得出。这种方式人为地造成了24 h GNSS数据周期与主要分潮周期不一致,因为主要分潮的周期并非是24 h的倍数,其残差导致了伪周年项的产生和系统性差异。同时,单天解也由于未知数的剧增降低了估值的解算强度。另外,部分分潮周期与GNSS轨道及部分误差改正项的周期相近,容易产生耦合效应。如半日周期分潮(M2、S2、N2、K2)信号与GNSS卫星轨道和电离层的周期相近,容易与GNSS卫星轨道和电离层延时的残差相互影响。同理,周日分潮(K1、O1、P1、Q1)信号与对流层延时、光压摄动信号发生耦合,而板块运动、站址升降、卫星钟差和天线极化等因素引起的站址运动也容易与较长周期的海洋分潮相互混淆。
3 结 语从通过引入海潮负荷位移以提高GNSS定位精度,发展到利用GNSS技术监测海潮负荷所引起的GNSS站址的周期性变化,GNSS反演海潮负荷效应(主要是位移)的研究得到了长足的发展。国内外研究人员利用GNSS反演的海潮负荷位移模型与现有的海潮负荷位移模型相比较,在一些主要分潮上得到了比较理想的结果。但现有的海潮负荷位移模型的精度还不能满足IERS规范所期望的精度,尤其是沿海地区受浅水效应影响,相比其他地区精度欠佳,此问题现在还不能从根本上解决。另外,在反演方法上还需要进一步完善和发展,尽量减少伪周年项的产生以及系统性差异。部分分潮与GNSS残差存在耦合效应,导致分潮的信号与GNSS卫星轨道和电离层延时的残差相互影响和混淆。因此,需要在理论和方法上进行更多的深入研究,提高利用GNSS数据反演海潮负荷位移模型的精度。
| [1] | Xu Xiaoqing.The Computation of Ocean Tidal Loading Effects in the Seas Adjacent to China and over the Continent of and near China[D].Qingdao:The First Institute of Oceanography,SOA,China, 2011 (徐晓庆.中国近海和中国及邻近大陆海潮负荷效应的计算[D].青岛:国家海洋局第一海洋研究所,2011) |
| [2] | Yuan Linguo,Ding Xiaoli,Sun Heping, et al.Determination of Ocean Tide Loading Displacements in Hong Kong Using GPS Technique[J].Sci China Earth Sci,2010, 40(6):699-714(袁林果,丁晓利,孙和平,等.利用技术精确测定香港海潮负荷位移[J].中国科学(地球科学),2010,40(6):699-714) |
| [3] | Sun Heping,Zhou Jiangcun.Correction Problem of the Ocean Loading Signals on Gravity Measurements at Fundamental Station Crust Movement Observation Network in China[J].Advance in Sciences,2002,17(1):39-43(孙和平,周江存.中国地壳运动观测网络基准站重力场变化的海潮负荷信号改正问题[J]. 地球科学进展,2002, 17(1):39-43) |
| [4] | Zhang Jie,Li Fei,Lou Yidong, et al.Ocean Tide Loading Effect on GPS Precise Positioning[J]. Geomatics and Information Science of Wuhan University, 2013,38(12):1 400-1 404(张杰,李斐,楼益栋,等.海潮负荷对GPS精密定位的影响[J].武汉大学学报·信息科学版,2013,38(12):1 400-1 404) |
| [5] | Farrell W E.Deformation of Earth by Surface Loads[J].Rev Geophys SpacePhys, 1972,10(3):761-797 |
| [6] | Francis O,Mazzega P.Global Charts of Ocean Tide Loading Effects[J].J Geophys Res,1990,95(C7):11 411-11 424 |
| [7] | Agnew D C.NLOADF:A Program for Computing Ocean-Tide Loading[J].J Geophys Res,1997,102(B3):5 109-5 110 |
| [8] | Bos M S, Baker T F.An Estimate of the Errors in Gravity Ocean Tide Loading Computations[J].Journal of Geodesy,2005,79(1-3):50-63 |
| [9] | Sun Heping, Xu Houze. Adaptability of the Ocean and Earth Tidal Models Based on Global Observations of the Superconducting Gravimeters[J]. Science in China Sereis D Earth Science, 2005, 48(11):649-657(孙和平,许厚泽.基于全球超导重力仪观测研究海潮和固体潮模型的适定性[J].中国科学辑地球科学,2005,35(7):649-657) |
| [10] | Baker T F,Bos M S.Validating Earth and Ocean Tide Models Using Tidal Gravity Measurements[J].Geophys J Int,2003,152(2):468-485 |
| [11] | Boy J P,Llubes M,Hinderer J,et al.A Comparison of Tidal Ocean Loading Models Using Superconducting Gravimeter Data[J].J Geophys Res,2003,108(B4,2 193):1-17 |
| [12] | Petrov L,Ma C P.Study of Harmonic Site Position Variations Determined by Very Long Baseline Interferometry[J].J Geophys Res,2003,108(B4,2 190):1-16 |
| [13] | Chen Xiandong.Ocean Tide Loading Correction in GPS Precise Positioning[J].Journal of Southeast Jiaotong University,2006,42(4):429-433(陈宪冬.精密定位中的海潮负荷改正[J].西南交通大学学报,2006,42(4):429-433) |
| [14] | Vergnolle M,Bouin M N,Morel L,et al.GPS Estimates of Ocean Tide Loading in NW-France:Determination of Ocean Tide Loading Constituents and Comparison with Recent Ocean Tide Model[J].Geopgys J Int, 2008,173(2):444-458 |
| [15] | King M A,Penna N T,Clarke P J,et al.Validation of Ocean Tide Models Around Antarctica Using Onshore GNSS and Gravity Data[J].J Geophys Res-Sol Earth,2005, 110(B08401):1-21 |
| [16] | Thomas I D,King M A, Clarke P J. A Comparison of GNSS,VLBI and Model Estimates of Ocean Tide Loading Displacements[J].Geodesy,2007,81(5):359-368 |
| [17] | King M.Kinematic and Static GNSS Techniques for Estimating Tidal Displacements with Application to Antarctica[J].J Geodyn, 2006, 41(1-3):77-86 |
| [18] | Lambert A,Pagiatakis S D,Billyard A P, et al. Improved Ocean Tide Loading Corrections for Gravity and Displacement:Canada and Northern United States[J].Journal of Geophysical Research,1998,103(B12):30 231-30 244 |
| [19] | Dragert J, Lambert A.Ocean Loading Corrections for Continuous GNSS:A Case Study at the Canadian Coastal Site Holberg[J].Geophysical Research Letters,2000,27(14):2 045-2 048 |
| [20] | Zerbini S,Matonti F,Raicich F,et al.Observing and Assessing Nontidal OceanLoading Using Ocean,Continuous GNSS and Gravity Data in the Adriatic Area[J].Geophysical Research Letters,2004,31(L23609):1-5 |
| [21] | Muriel L,Florsch N,Boy J P,et al.Multi-technique Monitoring of Ocean Tide Loading in Northern France[J].C R Geoscience,2008,340(6):379-389 |
| [22] | Melachroinos S A,Llubes R B, Perosanz F. Ocean Tide Loading Displacements from Global and Local Grids:Comparisons to GNSS Estimates over the Shelf of Brittanny,France[J].Journal of Geodesy,2008,82(6):357-371 |
| [23] | Clarke P J, Penna N T.Ocean Tide Loading and Relative GNSS in the British Isles[J].Survey Revies,2010,42(317):212-228 |
| [24] | McCarthy D D, Petit G.IERS Technical Note No.32[EB/OL].http://www.iers.org/IERS/EN/Publications/TechnicalNotes/tn32.html, 2003 |
| [25] | Dach R, Dietrich R.Influence of the Ocean Loading Effect on GNSS Derived Precipitable Water Vapor[J].Geophysical Research Letters,2000,27(18):2 953-2 958 |
| [26] | Shum C K,Woodworth P L,Andersen O B,et al.Accuracy Assessment of Recent Ocean Tide Models[J].Journal of Geophysical Research,1997, 102(C11):25 173-25 194 |
| [27] | King M A,Penna N T,Clarke P. Validation of Ocean Tide Models around Antarctica Using onshore GNSS and Gravity Data[J].Journal of Geophysical Research,2005,110(B08401):1-21 |
| [28] | Penna N T,Bos M S,Baker T F,et al.Assessing the Accuracy of Predicted Ocean Tide Loading Displacement Values[J].Journal of Geodesy, 2008, 82(12):893-907 |
| [29] | Urschl C,Dach R,Hugentobler U,et al.Validating Ocean Tide Loading Models Using GNSS[J].Journal of Geodesy,2005,78(10):616-625 |
| [30] | Hwang C.Coastal Gravity Anomalies from Retracked Geosat/GM Altimetry:Improvement, Limitation and the Role of Airborne Gravity Data[J]. Journal of Geodesy, 2006,80(4):204-216 |
| [31] | Matsumoto K,Takanezawa T, Ooe M.Ocean Tide Models Developed by Assimilating TOPEX/POSEIDON Altimeter Data into Hydrodynamical Model:A Global Model and a Regional Model Around Japan[J].Journal of Oceanography, 2000, 56(5):567-581 |
| [32] | Yun H S,Lee D, Song D.Determination of Vertical Displacements over the Coastal Area of Korea Due to the Ocean Tide Loading Using GNSS Observation[J].Journal of Geodynamics,2007,43(4/5):528-541 |
| [33] | Zhang Hanwei,Zheng Yong,Zhao Fangquan.Theoretical Research of Ocean Loading Tide Influence on Station Displacements[J].Journal of Geodesy and Geodynamics, 2003, 23(1):69-73(张捍卫,郑勇,赵方泉.海洋负荷潮汐对测站位移影响的理论研究[J].大地测量与地球动力学,2003,23(1):69-73) |
| [34] | Zhou Jiangcun,Sun Heping.The Load Effect of Local Tide on Displacement[J].Progress in Geophysics,2007,22(5):1 340-1 344(周江存,孙和平.近海潮汐效应对测站位移的负荷影响[J].地球物理学进展,2007,22(5):1 340-1 344) |
| [35] | King M.Kinematic and Static GNSS Techniques for Estimating Tidal Displacements with Application to Antarctica[J].Journal of Geodynamics,2006,41(1-3):77-86 |
| [36] | Dam T V,Ahr J W, Lavallee D.A Comparison of Annual Vertical Crustal Displacements from GNSS and Gravity Recovery and Climate Experiment(GRACE) over Europe[J].J Geophysical Res,2007,112(B03404):1-11 |
| [37] | Greaves M,Bingley R,Baker D, et al.National Report of Great Britain, 2004[C].The Symposium of the IAG Sub-commission for the European Reference Frame,Bratislava,Slovakia,2004 |
| [38] | Yuan L G,Ding X L,Zhong P,et al.Estimation of Ocean Tide Loading Displacements and Its Impact on Position Time Series in Hong Kong Using a Dense Continuous GNSS Network[J].Journal of Geodesy,2009,83(11):999-1 015 |
| [39] | Yuan L G,Chao B F,Ding Xiaoli,et al.The Tidal Displacement Field at Earth's Surface Determined Using Global GNSS Observations[J].Journal of Geophysical Research:Solid Earth,2013,118(1):2 618-2 632 |
 2016, Vol. 41
2016, Vol. 41



