文章信息
- 董箭, 彭认灿, 张立华, 汪志军
- DONG Jian, PENG Rencan, ZHANG Lihua, WANG Zhijun
- 利用滚动圆变换的多波束测深数据滤波算法
- An Algorithm of Filtering Noises in Multi-beam Data Based on Rolling Circle Transform
- 武汉大学学报·信息科学版, 2016, 41(1): 86-92
- Geomatics and Information Science of Wuhan University, 2016, 41(1): 86-92
- http://dx.doi.org/10.13203/j.whugis20130757
-
文章历史
- 收稿日期: 2013-11-16

2. 海军司令部航海保证部, 北京, 100841
2. The Navigation Guarantee Department of the Chinese Navy Head Quarters, Beijing 100841, China
采用多波束测深系统获取海底地形信息是进行海洋测量和从事海洋研究的重要手段之一[1]。与陆地测量相比,海洋测量存在众多不稳定因素,如仪器噪声、海况因素或多波束参数设置不合理等,使得测量数据中含有少量的异常数据。此外,受环境等因素的影响,数据中还存在较小的随机噪声[2, 3, 4, 5]。为提高海底地形的精度必须对多波束测深数据进行滤波处理,消除虚假信号,恢复、保留真实信息。传统的多波束测深数据滤波通常采用人工滤波的方法,但由于多波束测深数据量十分庞大,数据处理的任务越来越繁重,传统的手工作业模式已不能满足海量多波束测深数据的处理要求。此外,人工滤波大量采用类似“除草”的作业方式,带有较强的主观性,使得处理后的海底地形非常平滑,但这种处理方法有可能会导致出现海底微地貌或小型障碍物被不合理删除的情况[5, 6]。因此,有必要研究快速、可靠的数据滤波方法。
国内外学者已在测深异常数据检测方面取得了不少的成果。文献[5]根据邻域内测深数据的统计特性,提出了一种基于门限值的深度门滤波算法。Simrad公司对该算法进行了改进,但这类算法的门限值大都依赖于海洋测量人员的经验,人工干预较大[6]。文献[7]根据实测波束脚印的深度和平面位置,采用多项式曲面函数拟合地形,提出了多波束测深数据的趋势面滤波算法。该类算法操作相对简单,对于地势起伏相对平坦的情况较为适用,但若地形变化复杂则会导致滤波不彻底[8]。文献[9]在总结前人算法的基础上,根据较大区域的测深数据的分布特性,提出了一种基于中值滤波、局部方差检测和小波分析的混合算法来定位异常数据,并滤去随机噪声,取得了较好的滤波效果,但对于算法中小波及中值滤波的相关参数的选择和设定则未作过多讨论[10]。CUBE算法具有良好的异常数据检测效果,现已成为CARIS HIPS软件中的一个重要模块。但由于某些原因,国内对于CUBE算法的研究大都停留在理论层面。此外,由于多波束测量的特殊性,在没有先验信息的条件下,对于测量数据中所存在的各类异常数据,通常难以区分其究竟属于虚假信号还是来自某一类特殊地形或人工要素(如海底微地貌或井架等)的回波信号,这造成了多波束测深数据处理中异常信号的二义性问题[6, 7, 8, 9, 10]。二义性问题一方面使得多波束滤波算法效果难以形成明确的评价准则,另一方面,没有先验信息的条件下,现有自动滤波算法存在过分追求人工滤波效果的倾向,使得滤波后的海底地形往往过于平滑。
《海道测量规范》中规定,原则上必须连续记录3~5个回波信号才能够在记录纸上辨别一个小目标[6, 14]。这为解决上述异常信号的二义性问题提供了一定准则,即对于多波束测深数据的滤波除了要考虑异常信号与测深数据统计特性的差异外,还需依据连续回波信号数目进一步判断异常信号属于特殊地形或人工要素的可能性。缓冲区分析是地理信息系统中基本的空间分析功能之一,是对空间要素特征进行度量的一种重要方法[11]。基于缓冲区分析功能的滚动圆变换算法在平面要素的凹凸性分析和最小凸包的提取中应用广泛[12]。本文在分析滚动圆变换算法原理实质的基础上,针对以Ping为处理单元的多波束测深数据,利用滚动圆变换结合连续回波信号数目对其凹凸性进行定量识别和分析,并顾及Ping内测深数据的统计特性,建立异常信号判定准则,在保持海底地形完整性的基础上,实现对多波束测深数据进行快速滤波的目的。
1 滚动圆变换构建原理及其几何特性分析 1.1 线要素缓冲区边界变换对于分布轴线为{Q1,…,QN+1}的线要素T,其左、右侧缓冲区边界变换KL(r)、KR(r)的数学定义为[12, 13]:
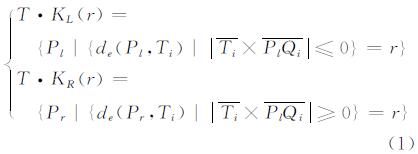
式中,r表示缓冲距;T·KL(r)、T·KR(r)分别表示线要素T的左、右侧缓冲区边界;Pl、Pr分别表示T·KL(r)、T·KR(r)上任意点;Ti表示线要素T上任意线段;de表示二维欧氏求距运算;×表示向量积运算。
1.2 滚动圆变换构建原理滚动圆变换是指由二维平面上一无限光滑的圆环沿线要素一侧滚动而形成一内痕迹线的一种几何变换,滚动圆变换有左右侧之分[12]。数学形式上,滚动圆变换等价于线要素左(右)侧缓冲区边界的变换组合[12, 13]。滚动圆变换的数学定义为[12]:
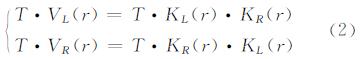
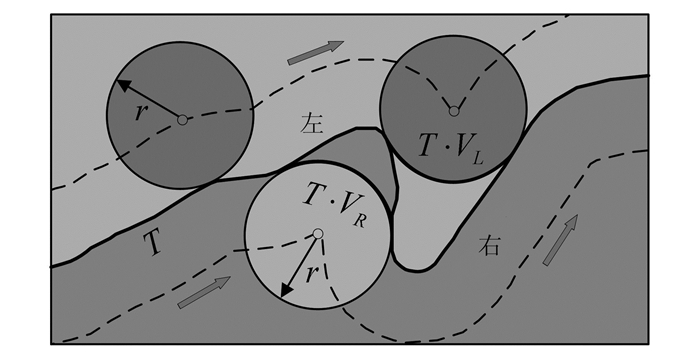
式中,VL(r)、VR(r)分别表示左(右)侧滚动圆变换。如图1所示,对于给定线要素T,经由左侧滚动圆变换VL(r)所得到的曲线T·VL(r)具有保持凸部不变、缩小或填平凹部的特性;而经由右侧滚动圆变换VR(r)所得到的曲线T·VR(r)则具有保持凹部不变、缩小或削平凸部的特性。
|
| 图 1 滚动圆变换示意图 Fig. 1 Diagram Map of Rolling Circle Transform |
滚动圆变换中,阈值(缓冲距r)的大小决定了其对线要素的空间几何形态影响程度。对于二维平面上任一线要素而言,其凹(凸)部的填平(削平)程度与缓冲距r存在如下函数关系[13]:
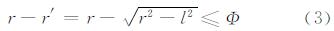
式中,r′表示滚动圆中心与完全填平(削平)后的凹(凸)部中心的距离;l表示凹(凸)部宽度的一半;Φ(Φ≥0)表示凹(凸)部的填平程度。Φ越小,则凹(凸)部的填平(削平)程度越高;反之,则凹(凸)部的填平(削平)程度越低。
如图2所示,P为凹部特征点,Pl为左侧滚动圆中心,Plr、Prl分别为凹部经由左(右)侧滚动圆变换VL(r)(VR(r))所对应的特征点。PlrPrl的大小可理解为凹部特征点P处起伏程度的定量描述。PlPlr与线段AB相交于P′lr,P′lrPlr的大小Φ反映了凹部的填平程度,即凹部特征点P处起伏程度的定量描述精度。
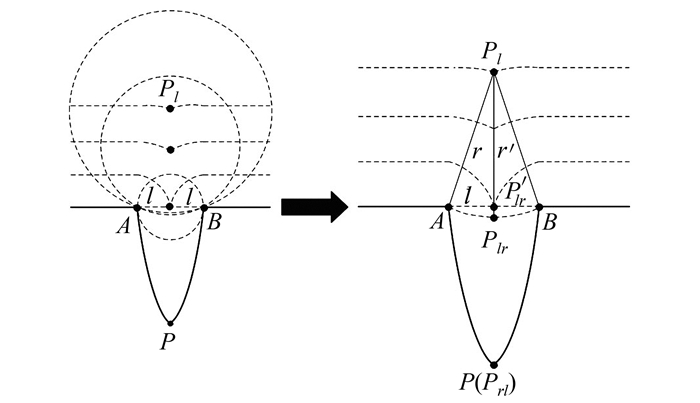
|
| 图 2 滚动圆变换的几何特性分析 Fig. 2 Geometry Characteristic of Rolling Circle Transform |
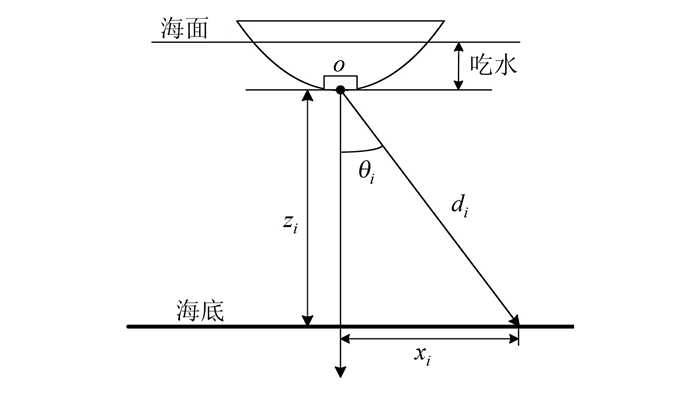
多波束测深系统采用发射、接收指向性正交的两组换能器阵获取一系列垂直于航向分布的窄波束,用Ping表示。测深中心坐标系中,Ping的数学定义为[6, 7]:
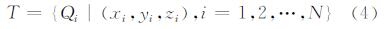
式中,Qi表示Ping内任意波束测深点;xi、yi、zi表示波束测深点Qi在测深中心坐标系中的三维分量;N表示Ping内波束测深点Qi的数量。在忽略声线弯曲的条件下,xi、yi、zi可由式(5)解算获得:
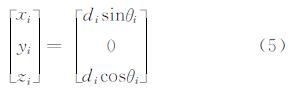
式中,di(di=Cti/2)表示回波时间ti与系统声速C乘积的一半;θi表示第i个波束的入射角,即:
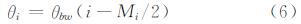
式中,θbw表示波束角;Mi/2表示条带的中央波束号。
如图3所示,测深中心坐标系中,波束测深点Qi的三维分量xi、yi、zi仅与x轴、z轴相关(yi≡0),且xi、zi分量之间存在形如zi=f(xi)(f(xi)=xi/tanθi)的函数关系。因此,多波束测深数据的处理单元Ping符合二维条件下线要素的数学定义。
|
| 图 3 测深中心坐标系 Fig. 3 Bathymetric Center Coordinate System |
滚动圆变换的几何特性决定了其可在给定参数Φ,即满足一定精度条件下,对线要素一定尺度(参数l确定)的凹(凸)部进行定量识别和分析。实际应用中,参数l值选取的关键是确定一个海底凹(凸)部所具有的最小范围是多大,即多波束测量中的连续回波信号数目。《海道测量规范》中规定,原则上必须连续记录3~5个回波信号才能够在记录纸上辨别一个小目标[6, 14]。即:

式中,m(3≤m≤5)表示连续记录的回波信号数;δ表示波束脚印的平均宽度。结合文献[15]中的波束脚印解算模型,δ的数学定义为:
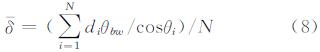
对于滚动圆变换中的另一重要参数Φ,其大小决定了滚动圆变换对于Ping内凹(凸)部描述的准确程度。为保证滚动圆变换具有较好的滤波效果,Φ可依据《海道测量规范》中水深测量的极限误差(置信度95%)来确定[15]。即:

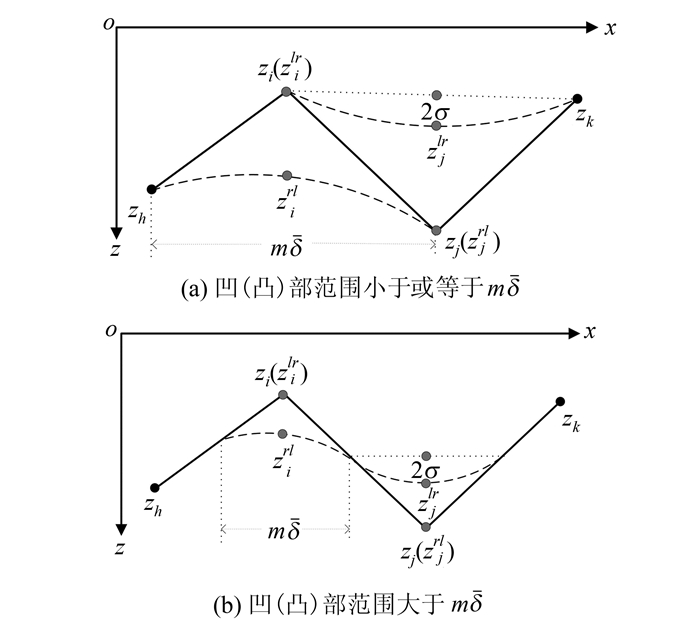
式中,σ表示水深测量的中误差。将式(7)、式(9)分别代入式(3),则阈值(缓冲距r)进一步限定为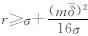 。如图4所示,zh、zi、zj、zk(h≤i≤j≤k)分别表示Ping内波束测深点Qh、Qi、Qj、Qk对应的水深值;Qi、Qj为Ping内相邻凸部和凹部特征点;zilr(zirl)、zjlr(zjrl)分别表示特征点Qi、Qj经由左(右)侧滚动圆变换VL(r)(VR(r))所对应特征点的水深值;|zilr-zirl|、|zjlr-zjrl|分别表示特征点Qi、Qj处海底地形的起伏程度。
。如图4所示,zh、zi、zj、zk(h≤i≤j≤k)分别表示Ping内波束测深点Qh、Qi、Qj、Qk对应的水深值;Qi、Qj为Ping内相邻凸部和凹部特征点;zilr(zirl)、zjlr(zjrl)分别表示特征点Qi、Qj经由左(右)侧滚动圆变换VL(r)(VR(r))所对应特征点的水深值;|zilr-zirl|、|zjlr-zjrl|分别表示特征点Qi、Qj处海底地形的起伏程度。
|
| 图 4 基于滚动圆变换的海底微地貌识别特性 Fig. 4 Characteristic of Identifying Micro Morphology Based on Rolling Circle Transform |
在缓冲距  且Φ=2σ)的前提下,对于凸部和凹部特征点Qi、Qj,若凹(凸)部范围小于或等于m δ(图4(a)中,xj-xh≤m且xk-xi≤m),则凹(凸)部被完全削平(填平);若凹(凸)部范围大于m(图4(b)中,xj-xh>m且xk-xi>m),则凹(凸)部被部分削平(填平),且凹(凸)部被削平(填平)的范围为m。上述分析看出,滚动圆变换具有在给定连续回波信号数目m的条件下,定量识别海底小目标的特性,且识别精度小于水深测量的极限误差2σ。滚动圆变换的此类特性,对于解决多波束测深数据处理中异常信号的二义性问题提供了一定的解决思路,即对于多波束测深数据的滤波除了考虑异常信号与测深数据统计特性的差异外,还需依据连续回波信号数目m进一步判断异常信号属于特殊地形或人工要素的可能性。
且Φ=2σ)的前提下,对于凸部和凹部特征点Qi、Qj,若凹(凸)部范围小于或等于m δ(图4(a)中,xj-xh≤m且xk-xi≤m),则凹(凸)部被完全削平(填平);若凹(凸)部范围大于m(图4(b)中,xj-xh>m且xk-xi>m),则凹(凸)部被部分削平(填平),且凹(凸)部被削平(填平)的范围为m。上述分析看出,滚动圆变换具有在给定连续回波信号数目m的条件下,定量识别海底小目标的特性,且识别精度小于水深测量的极限误差2σ。滚动圆变换的此类特性,对于解决多波束测深数据处理中异常信号的二义性问题提供了一定的解决思路,即对于多波束测深数据的滤波除了考虑异常信号与测深数据统计特性的差异外,还需依据连续回波信号数目m进一步判断异常信号属于特殊地形或人工要素的可能性。
由§2.3节中分析可知,在给定l、Φ的前提下,PlrPrl的大小反映了凹(凸)部特征点P相对于Ping内测深数据的起伏程度。令Error(i)代表波束测深点Qi的信号状态值(0表示异常信号;1表示正常信号),在海底地形变化光滑连续、平缓的假设下,本文建立如下多波束测深数据滤波准则:
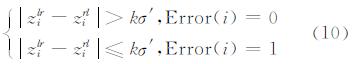
式中,zilr表示波束测深点Qi经由左侧滚动圆变换后的对应水深值;zirl表示波束测深点Qi经由右侧滚动圆变换后的对应水深值;|zilr-zirl|表示波束测深点Qi处海底地形的起伏程度;k表示粗差判定因子;σ′表示Ping内测深数据起伏程度的中误差,可由式(11)解算获得,即:
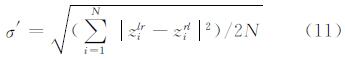
图5所示即为基于滚动圆变换的多波束测深数据滤波原理图。在由o-xz所构成的二维空间直角坐标系中,对于中心轴线为{Qi|(xi,zi),i=1,2,…,N}的单Ping测深数据,经由缓冲距r
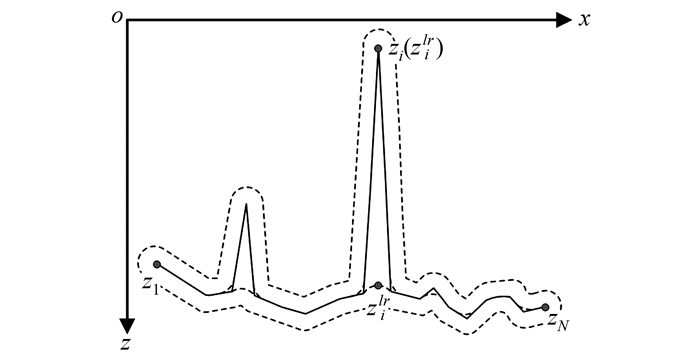
|
| 图 5 基于滚动圆变换的多波束测深数据滤波原理 Fig. 5 Principle of Filtering Noises in Multi-beam Data Based on Rolling Circle Transform |
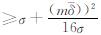 的左(右)侧滚动圆变换VL(r)(VR(r))后,其任意波束测深点Qi的地形起伏程度可由zilr、zirl的差值绝对值|zilr-zirl|确定。根据“小概率事件”判定法则,从统计意义上讲,当波束测深点Qi处海底地形的起伏程度大于2或3倍σ′时,可认为是小概率事件[3, 8]。故粗差判定因子k=2或3。
的左(右)侧滚动圆变换VL(r)(VR(r))后,其任意波束测深点Qi的地形起伏程度可由zilr、zirl的差值绝对值|zilr-zirl|确定。根据“小概率事件”判定法则,从统计意义上讲,当波束测深点Qi处海底地形的起伏程度大于2或3倍σ′时,可认为是小概率事件[3, 8]。故粗差判定因子k=2或3。
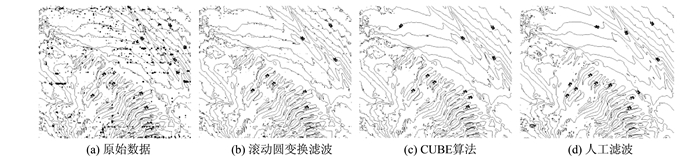
本文借助于文献[11]中线要素缓冲区构建原理,通过VC++编程实现了基于滚动圆变换的多波束测深数据滤波算法,并利用Surfer8.0软件对生成的实验结果进行了可视化显示与分析。实验环境为Celeron(R)处理器,主频为2.53 GHz,内存为512 M。实验采用的数据为我国东海某海区的多波束测深数据,共包含725 840个离散水深点,极限误差为1 m,连续记录的回波信号数m与粗差判定因子k分别设置为3和2,算法耗时2 578 s。为便于实验比对和分析,利用Surfer8.0软件中的加权平均法(取距离反比平方权作为权函数),对原始多波束测深数据,经本文算法、CUBE算法(算法耗时72 s)和人工滤波后的多波束测深数据进行了插值处理,形成229×200的格网DDM。图6、7所示分别为基于上述不同滤波方法的海底地形表面及等深线(等深距为5 m)对比图。

|
| 图 6 基于不同滤波方法的海底地形表面对比图 Fig. 6 Marine Topography Surface Generated by Different Filtering Noises Algorithm |
|
| 图 7 基于不同滤波方法的等深线对比图 Fig. 7 Bathymetric Contour Generated by Different Filtering Noises Algorithm |
从图6、7中可以看出,基于滚动圆变换的多波束测深数据滤波算法、CUBE算法和人工滤波方法均能有效剔除原始多波束测深数据中存在的粗差,说明本文算法对多波束测深数据具有良好的粗差判别与改正能力,且相对于以天为单位的人工滤波方法,其效率得到了较大提高。为进一步验证本文算法对多波束测深数据的滤波效果,对原始多波束测深数据,经本文算法、CUBE算法和人工滤波后的多波束测深数据中的水深极大值、水深极小值及水深均方根差进行了统计分析,结果见表1。
| 水深值统计 | 原始 数据 | 滚动圆 变换 | CUBE 算法 | 人工 滤波 |
| 极小值 | -103.329 | -99.437 | -99.071 | -98.774 |
| 极大值 | -1.553 | -13.204 | -13.263 | -12.836 |
| 均方根差 | 18.542 | 16.732 | 16.174 | 15.979 |
实验结果表明:(1) 由于粗差数据的影响,原始多波束测深数据的水深值范围及水深均方根差均较大。(2) 本文算法、CUBE算法和人工滤波后的多波束测深数据的水深极大值和极小值均相差较小,说明三者均滤去了原始多波束测深数据中的较大粗差。(3) CUBE算法、人工滤波后的多波束测深数据的水深均方根差均小于本文 算法所得到的相应水深均方根差,造成上述差异的主要原因在于经本文算法滤波后的多波束测深数据的水深值波动相对于海底地形的变化较小。CUBE算法由于是在设定的格网下选择水深,并对测区格网交叉点处进行水深及其相关误差估计,最终拟合海底趋势面,使得处理后的海底地形较为平滑。此外,人工滤波由于带有较多的先验信息和较大的主观性,使得处理后的海底地形表面更加平滑。
需要指出的是,表1中的实验结果分析只是从多波束测深数据水深值的角度进行了统计,所反映的是经三类方法处理后的海底地形起伏程度。经CUBE算法、人工滤波后的多波束测深数据形成的海底地形表面较为平滑,这样的平滑效果对于海底地形表达的精度保持究竟是优势还是缺点至今仍是个值得探讨的问题。如果海底地形变化较为复杂或者有障碍物时(如暗礁、沉船等),这样的平滑效果则可能会导致障碍物被不合理删除。本文算法在设计时充分考虑了基于滚动圆变换的海底微地貌识别特性,在一定精度条件下对给定范围的海底微地貌进行了保留。在统计结果上,尽管本文算法在海底地形起伏程度上相对于CUBE算法和人工滤波方法变化较小,在一定程度上说明了本文算法有利于海底微地貌的保留,较好解决了多波束测深数据处理中存在的异常信号的二义性问题。
4 结 语本文从滚动圆变换原理出发,通过对滚动圆变换几何特性的分析,针对以Ping为处理单元的多波束测深数据,提出了基于滚动圆变换的多波束测深数据滤波算法,并从理论上分析了缓冲距对滚动圆变换滤波效果的影响。实验结果表明,该算法能在保持海底地形完整性的基础上较好地滤除多波束测深数据中的粗差数据,且相对于人工滤波方法效率大为提高。但需要指出的是,算法解算过程中,所涉及的连续记录的回波信号数与粗差判定因子等参数均采用的是《海道测量规范》中给出的经验参数,理论性和通用性有待加强,需进一步研究如何根据实际多波束测深数据中各Ping的水深分布情况进行自适应估计。另外,考虑到多波束测深数据量规模较大(甚至海量),还必须研究算法的优化问题。
| [1] | Huang Motao, Zhai Guojun, Wang Rui, et al. The Detection of Abnormal Data in Marine Survey[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(3):269-276(黄谟涛, 翟国君, 王瑞, 等. 海洋测量异常数据的检测[J]. 测绘学报, 1999, 28(3):269-276) |
| [2] | Huang Xianyuan, Zhai Guojun, Huang Motao, et al. The Study of Constructing Trend Surface by Least Square Support Vector Machine[J]. Hydrographic Surveying and Charting, 2010, 30(3):9-12(黄贤源, 翟国君, 黄谟涛, 等. 最小二乘支持向量机构造海底趋势面研究[J]. 海洋测绘, 2010, 30(3):9-12) |
| [3] | Dong Jiang, Ren Lisheng. Filter of MBS Sounding Data Based on Trend Surface[J]. Hydrographic Surveying and Charting, 2007, 27(6):25-28(董江, 任立生. 基于趋势面的多波束测深数据滤波方法[J]. 海洋测绘, 2007, 27(6):25-28) |
| [4] | Wang Haidong, Chai Hongzhou, Song Guoda, et al. Principal Components Estimation of Trend Surface Coefficients in Multibeam Bathymetry[J]. Hydrographic Surveying and Charting, 2009, 29(5):5-7(王海栋, 柴洪洲, 宋国大, 等. 多波束测深趋势面系数的主成分估计[J]. 海洋测绘, 2009, 29(5):5-7) |
| [5] | Xu Weiming, Liang Kailong, Qiu Wendong. Optimum Wavelet Threshold Filtering Algorithm for Echosounding Signal Processing[J]. Acta Geodaetica et Cartographica Sinica, 1999, 28(2):133-138(徐卫明, 梁开龙, 邱文东. 测深信息处理的最佳小波门限滤波法[J]. 测绘学报, 1999, 28(2):133-138) |
| [6] | Zou Yonggang, Xiao Fuming, Liu Yanchun, et al. Automatic Depth Threshold Algorithm for Gross Error in Echo Sounding Signal Processing[J]. Science of Surveying and Mapping, 2009, 34(5):81-83(邹永刚, 肖付民, 刘雁春, 等. 应用自动可变深度门剔除伪异常水深信号方法[J]. 测绘科学, 2009, 34(5):81-83) |
| [7] | Li Jiabiao. Theory and Technology of Multibeam Exploratory Survey[M]. Beijing:China Ocean Press, 1999.(李家彪. 多波束勘测原理与技术方法[M]. 北京:海洋出版社, 1999) |
| [8] | Wang Haidong, Chai Hongzhou, Zhai Tianzeng, et al. Comparison of Two Trend Surface Detection Algorithms of Multibeam Bathymetry Outlier[J]. Marine Science Bulletin, 2010, 29(2):182-186(王海栋, 柴洪洲, 翟天增, 等. 多波束测深异常的两种趋势面检测算法比较[J]. 海洋通报, 2010, 29(2):182-186) |
| [9] | Yang Fanlin, Liu Jingnan, Zhao Jianhu. Detecting Outliers and Filtering Noises in Multi-beam Data[J]. Geomatics and Information Science of Wuhan University, 2004, 29(1):80-83 (阳凡林, 刘经南, 赵建虎. 多波束测深数据的异常检测和滤波[J]. 武汉大学学报·信息科学版, 2004, 29(1):80-83) |
| [10] | Zhang Juqing, Liu Pingzhi. Combining Fitting Based on Robust Trend Surface and Orthogonal Multiquadrics with Application in DEM Fitting[J]. Acta Geodaetica et Cartographica Sinica, 2008, 11(4):526-530(张菊清, 刘平芝. 抗差趋势面与正交多面函数结合拟合DEM数据. 测绘学报, 2008, 11(4):526-530) |
| [11] | Zhu Changqing, Shi Wenzhong. Spatial Analysis Modeling and Theory[M]. Beijing:Science Press, 2006(朱长青, 史文中. 空间分析建模与原理[M]. 北京:科学出版社, 2006) |
| [12] | Christensen A H J. Cartographic Line Generalization with Waterlines and Medial-Axes[J]. Cartography and Geographic Information Science, 1999, 26(1):19-32 |
| [13] | Dong Jian, Peng Rencan, Zhang Lihua. Multi-scale Representation of Digital Depth Model Based on Rolling Ball Transform[J]. Journal of Geo-information Science, 2012, 14(6):704-711(董箭, 彭认灿, 张立华, 等. 滚动球变换的数字水深模型多尺度表达[J]. 地球信息科学学报, 2012, 14(6):704-711) |
| [14] | Wu Yingzi. A Study on Multi-beam Sounding System Seafloor Tracking & Data Processing Techniques[D].Harbin:Harbin Engineering University, 2001(吴英姿. 多波束测深系统地形跟踪与数据处理技术研究[D]. 哈尔滨:哈尔滨工程大学, 2001) |
| [15] | Liu Yanchun, Xiao Fumin, Bao Jingyang, et al. Introduction to Hydrogrophy[M]. Beijing:Surveying and Mapping Press, 2006(刘雁春, 肖付民, 暴景阳, 等. 海道测量学概论[M]. 北京:测绘出版社, 2006) |
 2016, Vol. 41
2016, Vol. 41



