文章信息
- 邓文彬, 许闯, 阿力甫·努尔买买提
- DENG Wenbin, XU Chuang, Allfu·Nurmmamat
- 卫星重力梯度观测数据的时变信号影响分析
- Effect of Time-Varying Gravity Signal on Satellite Gravity Gradient Observations
- 武汉大学学报·信息科学版, 2016, 41(1): 72-78
- Geomatics and Information Science of Wuhan University, 2016, 41(1): 72-78
- http://dx.doi.org/10.13203/j.whugis20140861
-
文章历史
- 收稿日期: 2014-11-14

2. 新疆大学建筑工程学院测绘工程系, 新疆 乌鲁木齐, 830046;
3. 华中科技大学物理学院基本物理量测量教育部重点实验室, 湖北 武汉, 430074
2. School of Architectural Engineering, Xinjiang University, Urumchi 830046, China;
3. MOE Key Laboratory of Fundamental Physical Quantities Measurement, School of Physics, Huazhong University of Science and Technology, Wuhan 430074, China
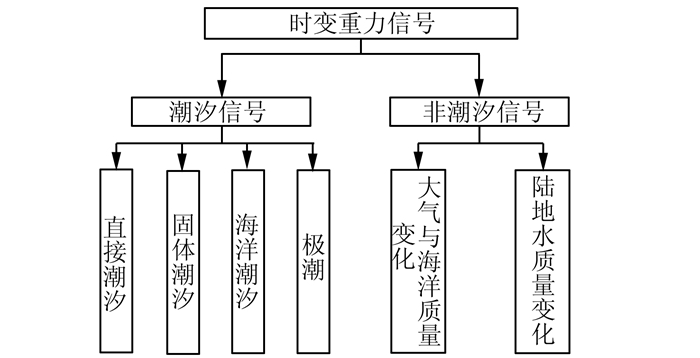
卫星重力梯度技术是利用重力梯度仪直接测量地球引力位的二阶导数,被认为是21世纪初期确定全球重力场最有效的技术之一。重力场和静态海洋环流探测卫星(gravity field and steady-state ocean circulation explorer,GOCE)是人类首次利用卫星重力梯度技术测定全球重力场。该卫星同时采用高低卫-卫跟踪测量和卫星重力梯度测量技术,其预期科学目标是以70 km空间分辨率、1 mGal重力异常和1~2 cm大地水准面的精度确定全球静态地球重力场[1,2,3]。为实现这一目标,必须对GOCE卫星重力梯度测量数据进行预处理,扣除粗差、系统偏差、有色噪声等。GOCE重力梯度数据的预处理主要是对Level 1b数据的处理,由欧洲空间局GOCE卫星高级数据处理部门完成,主要包括时变重力信号改正、粗差探测、外部校准与误差估计,并提供快速解和精密解两种模式的成果[4, 5]。时变重力信号可以分为潮汐和非潮汐部分:潮汐部分包括直接潮汐、地球固体潮汐、海洋潮汐和极潮等;非潮汐部分包括大气与海洋质量变化和陆地水质量变化等,如图1所示。
|
| 图 1 时变重力信号主要影响因素 Fig. 1 Main Influences of Time-Varying Gravity Signal |
文献[6]详细分析了时变重力信号中的潮汐改正,文献[7]系统讨论了极潮的影响,文献[8]则给出了陆地水质量变化的影响,文献[9]研究了陆地水质量变化与冰雪质量变化的季节效应。文献[10]利用模拟卫星轨道数据,分析了日月引力、固体潮、海潮、大气潮和固体极潮等保守力对GOCE卫星运动和重力梯度观测值的影响。文献[11, 12]利用模拟轨道数据研究了250 km高空处卫星重力梯度观测数据的时变重力改正。目前,GOCE卫星已经有实测数据,各项潮汐与非潮汐改正通过官方网站公布,但并没有提供详细的解算模型及相关计算软件。因此,本文将详细分析潮汐和非潮汐信号对GOCE卫星重力梯度观测数据的影响,并与GOCE官方公布结果进行对比,来验证本文计算方法的正确性与有效性。
1 卫星重力梯度观测数据的时变重力改正方法 1.1 潮汐影响 1.1.1 直接潮汐改正GOCE卫星在运行过程中除了受到地球引力之外,必然会受到太阳、月球以及其他星体的影响。直接潮汐就是指除地球以外其他天体引力对卫星产生的影响,其计算公式可以表示为[13, 14]:
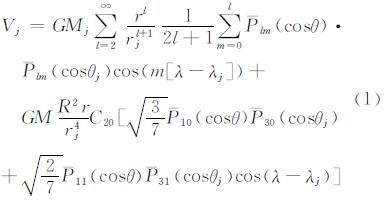
式中,Vj为第j个天体对卫星的引潮力位;G为万有引力常数;Mj为第j个天体的质量;r,θ,λ为GOCE卫星质心坐标;rj,θj,λj为第j个天体质心坐标;Plm(l为阶,m为次)为规格化的缔合Legendre函数;M和R分别为地球质量和平均半径。分别对r、θ、λ求二阶偏导,即可获取重力梯度分量[15, 16]。
1.1.2 固体潮汐改正在太阳、月球及其他天体的引潮力作用下,地球陆地部分会产生周期性形变现象,称之为固体潮。固体潮对GOCE卫星轨道产生的影响主要包括几何潮汐和动力潮汐[12],其计算分为三步。
第一步,计算二阶和三阶固体潮汐对重力场位系数(ΔClm和ΔSlm)的影响[17]:
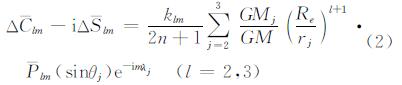
式中,i为复数的虚部;klm为与频率无关的标称勒夫数;Re为地球赤道半径。
第二步,计算二阶固体潮对四阶位系数的耦合影响:

其中,k2m(+)为勒夫数。
第三步,计算与频率相关的周日潮、半日潮及长周期潮改正。周日潮与半日潮改正公式为:
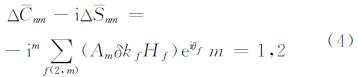
式中,Am为与地球平均半径R相关的参数;δkf、Hf和θf分别为频率f分潮波所对应的勒夫数改正值、振幅与幅角。长周期潮改正的计算公式为:
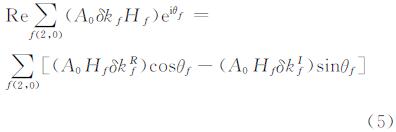
其中,δkfR与δkfI为别为δkf的实部与虚部。
1.1.3 海洋潮汐改正在太阳、月球及其他天体的引潮力作用下,除了地球陆地部分会产生周期性形变现象以外,海面也具有周期性的起伏变化,称之为海潮。海潮使得海洋的质量分布及其在地壳上的负荷发生时间变化,并引起地球产生相应的形变,进而对GOCE卫星轨道产生影响,其影响可以表示为对重力场位系数的改正[17]:

式中
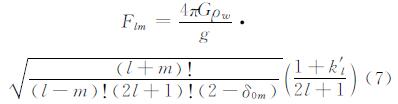
式中,ρw为海水密度;g为地球赤道平均重力加速度;k′l是负荷形变系数;Cflm±与Sflm±为频率f分潮波所对应的海潮系数。
1.1.4 极潮改正极潮是地壳对地球自转轴指向变化的弹性响应,其对GOCE卫星轨道的影响可以表示为[17]:
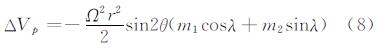
式中,Ω是地球平均自转角速度;m1、m2为极移动颤动变量。
1.2 非潮汐影响 1.2.1 大气与海洋质量变化改正大气运动常常会伴随着温度、湿度和气压系统的变化,使得大气和海洋、陆地之间不断进行着物质和能量的交换,从而引起重力场的变化,该时变信号属于大气的非潮汐影响。海洋在风力及科里奥利力的驱动下产生大尺度(大于500 km)的环流运动和中小尺度的高频涡流运动,同时,大气压强的变化也会引起海面地形起伏,从而引起重力场的时变,该时变信号属于海洋的非潮汐影响。采用球谐分析的方法来计算大气和海洋对卫星产生的引力位ΔV[18]:
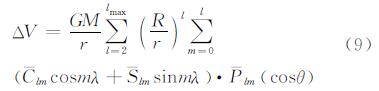
式中,系数 Clm和 Slm可直接从GRACE数据产品GAA、GAB、GAC中读取。对式(9)求二阶导数,即可得到重力梯度。
1.2.2 陆地水质量变化改正陆地上的水循环包括降水与蒸发、地表径流和地下水等,陆地水的循环过程会引起重力场的时变。GRACE的L2数据产品提供的GSM(G表示位系数,S表示GRACE数据估计,M表示静态重力场估计) )重力场模型移除了潮汐和非潮汐的大气与海洋的影响,几乎只包含了静态重力场以及除大气、海洋以外的所有的非潮汐因素,主要是指陆地水文的变化,包含了冰川均衡调整、地震等因素。因此,设法扣除掉GSM数据中的静态重力场部分,就可以得到陆地水文对重力场影响的球谐系数。本文采用的方法是在待求月份的GSM数据基础上扣除该年GSM数据的平均值,得到该月的球谐系数残差ΔCnm和ΔSnm,这一残差系数就是该月陆地水文相对于该年均值的波动。然后使用这些残差系数,并利用卫星激光测距获得的C20来替代GSM产品中的C20项,按照上述大气和海洋非潮汐影响的改正方法,可算出陆地水文变化对重力梯度的影响[18]。
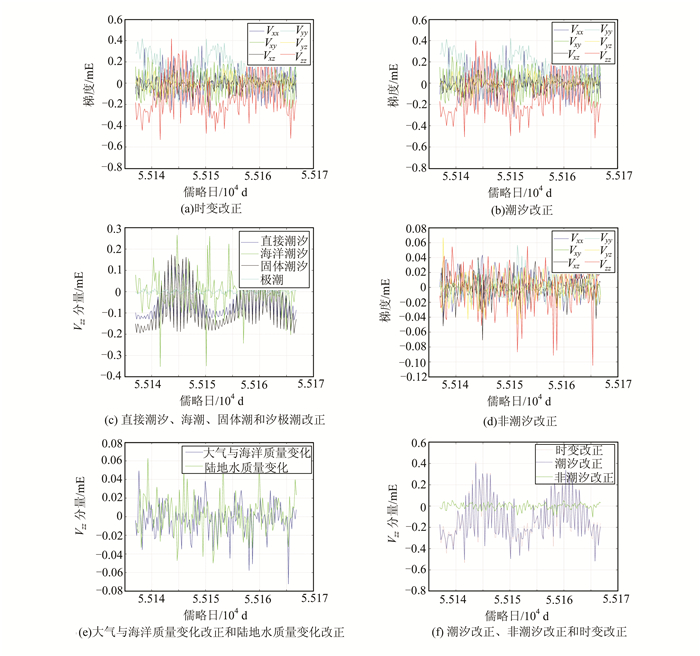
2 数值计算与分析采用2009-11-01~2009-12-01 GOCE卫星真实轨道数据、星历数据、勒夫数、海潮模型(CSR4.0)及地球自转参数(Eopc04)计算重力场位系数,获取潮汐改正。然后,由GAA、GAB、GAC和GSM模型(GRACE产品)计算非潮汐改正。最后,经坐标转换(从地固坐标系转换到局部指北坐标系),得到时变重力改正的6个梯度分量(Vxx、Vxy、Vxz、Vyy、Vyz和Vzz)结果。图2(a)为GOCE卫星重力梯度测量数据时变改正的6个分量Vxx、Vxy、Vxz、Vyy、Vyz和Vzz,其量级为0.1 mE (1 mE=10-12s-2)。重力梯度6个分量的变化趋势和幅度各不相同,Vzz变化幅度最大,Vxz变化幅度最小。GOCE卫星重力梯度测量数据的时变改正由潮汐改正和非潮汐改正叠加而来,潮汐改正和非潮汐改正结果如图2(b)和图2(d)所示。
|
| 图 2 GOCE卫星重力梯度观测数据的时变信号影响 Fig. 2 Effect of Time-Varying Signal on GOCE Satellite Gravity Gradient Observations |
图2(b)为潮汐改正的6个分量,从图2(b)中可知,GOCE卫星重力梯度测量数据的潮汐改正量级处于0.1 mE,其中,Vzz变化幅度最大,Vxz变化幅度最小。重力梯度6个分量的变化趋势和幅度与图2(a)中时变改正基本一致,表明潮汐信号是时变改正的主要贡献者。GOCE卫星重力梯度测量数据的潮汐改正是由直接潮汐改正、海洋潮汐改正、固体潮改正和极潮改正叠加而来,这4种潮汐改正之间的关系如图2(c)所示。图2(c)为4种潮汐改正的Vzz分量,从图2(c)中可以看出,前3种潮汐的影响量级都处于0.1 mE。其中,海洋潮汐的影响最大,固体潮汐次之,直接潮汐略小,极潮的影响最小,与前三种潮汐不在一个量级上。另外,天文潮汐与固体潮的周期性较明显,海洋潮汐与极潮的变化趋势不规则。
图2(d)为非潮汐改正的6个分量,其量级处于0.01 mE,比潮汐改正要低一个量级,其中,Vzz变化幅度最大,Vxz变化幅度最小。GOCE卫星重力梯度测量数据的非潮汐改正是由大气与海洋质量变化改正和陆地水质量变化改正叠加而来,这两种非潮汐改正Vzz分量之间的关系如图2(e)所示。由图2(e)可知,两种潮汐的影响量级都处于0.01 mE,变化趋势都不规则。
潮汐改正和非潮汐改正对GOCE卫星重力梯度测量数据的时变改正的贡献是不同的,如图2(f)所示。从图2(f)中可以看出时变改正和潮汐改正的变化趋势基本一致,非潮汐改正的变化幅度相对较小,表明潮汐改正是时变改正的主要贡献者,决定了时变改正的精度。潮汐改正具有较明显的周期性,属于有色噪声源,需在数据预处理中剔除。
表1为时变重力信号6个梯度分量对GOCE卫星重力梯度观测数据影响的取值范围。对于Vzz分量,潮汐影响范围为-0.897 1~0.600 2 mE, 非潮汐影响范围为-0.124 6~0.178 2 mE,时变改正在-0.927 3~0.613 1 mE范围内。可以看出,潮汐信号是时变重力信号的主要贡献者。另外,天文潮汐、海洋潮汐和固体潮汐处于同一量级(0.1 mE),极潮、大气和海洋质量变化、陆地水质量变化的影响在0.01 mE量级。
| 名称 | Vxx | Vxy | Vxz | Vyy | Vyz | Vzz |
| 直接潮汐 | max | 0.251 2 | 0.196 9 | 0.144 9 | 0.231 9 | 0.153 8 | 0.162 6 |
| min | -0.130 6 | -0.191 6 | -0.145 0 | -0.140 1 | -0.163 9 | -0.139 5 | |
| 海洋潮汐 | max | 0.330 3 | 0.132 6 | 0.330 0 | 0.311 7 | 0.279 1 | 0.545 7 |
| min | -0.317 0 | -0.141 0 | -0.348 5 | -0.340 8 | -0.353 6 | -0.642 0 | |
| 固体潮 | max | 0.134 2 | 0.047 2 | 0.138 4 | 0.137 0 | 0.153 5 | 0.225 7 |
| min | -0.124 9 | -0.046 7 | -0.135 1 | -0.100 8 | -0.141 1 | -0.206 4 | |
| 极潮 | max | 0.009 2 | 0.002 6 | 0.010 4 | 0.006 6 | 0.010 5 | 0.015 8 |
| min | -0.009 2 | -0.002 6 | -0.010 4 | -0.006 6 | -0.010 5 | -0.015 8 | |
| 大气与海洋质量变化 | max | 0.046 1 | 0.037 5 | 0.099 1 | 0.054 5 | 0.071 5 | 0.200 2 |
| min | -0.107 8 | -0.032 1 | -0.090 3 | -0.095 5 | -0.107 7 | -0.088 3 | |
| 陆地水质量变化 | max | 0.046 2 | 0.030 4 | 0.024 6 | 0.035 5 | 0.047 7 | 0.064 4 |
| min | -0.036 0 | -0.014 9 | -0.045 1 | -0.041 5 | -0.046 5 | -0.051 3 | |
| 潮汐 | max | 0.449 5 | 0.313 4 | 0.331 1 | 0.592 8 | 0.282 7 | 0.600 2 |
| min | -0.428 2 | -0.301 5 | -0.348 3 | -0.253 4 | -0.358 5 | -0.897 1 | |
| 非潮汐 | max | 0.062 1 | 0.032 5 | 0.079 1 | 0.079 6 | 0.079 6 | 0.178 2 |
| min | -0.093 1 | -0.034 1 | -0.086 2 | -0.088 5 | -0.111 0 | -0.124 6 | |
| 时变改正 | max | 0.447 4 | 0.313 9 | 0.329 | 0.600 4 | 0.311 8 | 0.613 1 |
| min | -0.405 2 | -0.299 9 | -0.340 3 | -0.260 0 | -0.371 5 | -0.927 3 |
为验证本文计算结果的正确性与有效性,将计算结果与GOCE卫星官方公布的时变改正结果进行比较。本文计算方法与GOCE官方数据处理方法存在一些细微差别:(1)GOCE官方选用FES2004海潮模型进行海潮改正;(2)GOCE官方采用欧洲中期天气预报中心分析结果与海洋环流和潮汐模型进行大气与海洋质量变化改正。因此,本文结果与GOCE卫星官方公布的时变改正结果可能会存在一些微小差异,本文主要关注其量级与趋势是否一致。
图3为本文结果与GOCE卫星官方公布的时变改正结果对比图。从图3中可知,二者的Vxx、Vxy、Vyy和Vzz分量在量级和趋势上具有较好的一致性;Vxz和Vyz在变化幅度上有些差异,但仍在同一数量级上,且变化趋势也存在一定相关性。从整体看,本文计算结果与GOCE卫星官方公布的时变改正结果吻合得较好,说明本文计算方法与结果是有效的。

|
| 图 3 本文计算结果与GOCE官方公布的时变改正结果 Fig. 3 Time-Varying Correction Results in this Paper and Official GOCE |
GOCE卫星重力梯度观测数据的预处理是实现其预期科学目标的重要任务之一。本文根据GOCE卫星轨道真实数据计算了时变重力信号对卫星重力梯度观测数据的影响,并与GOCE官方公布结果进行了对比。主要结论如下:(1) 本文计算结果与GOCE官方公布的时变改正结果,在量级和趋势上,具有较好的一致性;(2) 时变重力信号的影响量级处于0.1 mE,比GOCE的设计精度略低,但时变重力信号具有明显周期性,属于有色噪声源,在GOCE卫星重力梯度观测数据的预处理中必须对其进行改正;(3) 时变重力信号改正主要包括潮汐改正和非潮汐改正,其中非潮汐改正(0.01 mE)比潮汐改正(0.1 mE)低一个量级,潮汐信号改正决定了时变重力信号改正的精度;(4) 潮汐改正包括直接潮汐改正、海洋潮汐改正、固体潮汐改正和极潮改正,其中海洋潮汐的影响最大,固体潮汐次之,极潮影响最小;非潮汐改正包括大气与海洋质量变化改正和陆地水质量变化改正,两者影响相当。
| [1] | Balmino G, Beutler G, Ilk K H, et al. GOCE:Preparation of the GOCE Level 1 to Level 2 Data Processing[R]. Report PM 1 to the European Space Agency ESA, ESA/ESTEC, Noordwijk, The Netherlands, 2001 |
| [2] | ESA. Gravity Field and Steady-State Ocean Circulation Mission[R]. Reports for Mission Selection, the Four Candidate Earth Explorer Core Missions,The Netherlands, 1999 |
| [3] | Drinkwater M, Kern M. Calibration and Validation Plan for L1b Data Products, Technical Report[R]. EOP-SM/1363/MD-md, ESA ESTEC, Noordwijk, The Netherlands, 2006 |
| [4] | Gruber T,Rummel R, Abrikosov O, et al. GOCE Level 2 Product Data Handbook[R]. GP-MA-HPF-GS-0110, Issue 3.0, Paris, France, 2006 |
| [5] | Luo Zhicai, Wu Yunlong, Zhong Bo, et al. Pre-processing of the GOCE Satellite Gravity Gradiometry Data[J]. Geomatics and Information Science of Wuhan University, 2009, 34(10):1 163-1 167(罗志才,吴云龙,钟波,等. GOCE卫星重力梯度测量数据的预处理[J].武汉大学学报·信息科学版,2009,34(10):1 163-1 167) |
| [6] | Schrama E, Ray R. A Preliminary Tidal Analysis of TOPEX/POSEIDON Altimetry[J]. Journal of Geophysical Research, 1994, 99(C12):24 799-24 808 |
| [7] | Thomas M. Ocean Induced Variations of the Earth's Rotation-Results from a Simultaneous Model of Global Circulation and Tides[D]. Germany:University of Hamburg, 2002 |
| [8] | Schmidt R, Schwintzer P, Flechtner F, et al. GRACE Observations of Changes in Continental Water Storage[J]. Global and Planetary Change, 2006, 50:112-126 |
| [9] | Flechtner F. AODIB Product Description Document for Product Release 01 to 04[R]. Document GRACE, Issue3.1, Washington D C, USA, 2007 |
| [10] | Luo Zhicai,Zhong Bo, Ning Jinsheng, et al.Numerical Simulation and Analysis for GOCE Satellite Orbit Perturbations[J]. Geomatics and Information Science of Wuhan University, 2009, 34(7):757-760(罗志才, 钟波, 宁津生,等. GOCE卫星轨道摄动的数值模拟与分析[J]. 武汉大学学报·信息科学版, 2009, 34(7):757-760) |
| [11] | Zhong Bo. Study on the Determination of the Earth's Gravity Field from Satellite Gravimetry Mission GOCE[D]. Wuhan:Wuhan University, 2010(钟波. 基于GOCE卫星重力测量技术确定地球重力场的研究[D]. 武汉:武汉大学, 2010) |
| [12] | Wu Yunlong. Study on Pre-processing of GOCE Satellite Gravity Gradiometry Data[D]. Wuhan:Wuhan University, 2010(吴云龙. GOCE卫星重力梯度测量数据的预处理研究[D].武汉:武汉大学, 2010) |
| [13] | Hartmann T and Wenzel H G. The HW95 Tidal Potential Catalogue[J]. Geophysical Research Letters, 1995, 22(24):3 553-3 556 |
| [14] | Yang Guang. Temporal Gravity Field Corrections on Satellite Gravity Gradiometry Data[D]. Wuhan:Wuhan University, 2009(杨光.卫星重力梯度测量数据的时变重力场改正[D].武汉:武汉大学,2009) |
| [15] | Koop R. Global Gravity Field Modeling Using Satellite GravityGradiometry[R]. Netherlands Geodetic Mission, Publications on Geodesy, No.38, Delft, The Netherlands, 1993 |
| [16] | Luo Zhicai.The Theory and Methodology for Determining the Earth's Gravity Field Using Satellite Gravity Gradiometry Data[D]. Wuhan:Wuhan Technical University of Surveying and Mapping, 1996(罗志才.利用卫星重力梯度数据确定地球重力场的理论和方法[D].武汉:武汉测绘科技大学,1996) |
| [17] | McCarthy D D, Petit G. IERS Conventions 2003[R]. IERS Technical Note No.32, Verlag des Bundesamts fur Kartographie und Geodasie, Frankfurt am Main, 2004 |
| [18] | Zhu Guangbin, Li Jiancheng, Wen Hanjiang, et al.Study on Variations of Global Continental Water Storage with GRACE Gravity Field Models[J]. Journal of Geodesy and Geodynamics, 2008, 28(5):39-44(朱广彬,李建成,文汉江,等,利用GRACE时变重力位模型研究全球陆地水储量变化[J]. 大地测量与地球动力学,2008,28(5):39-44) |
 2016, Vol. 41
2016, Vol. 41


