文章信息
- 魏二虎, 刘文杰, WEI Jianan, 金双根, 刘经南
- WEI Erhu, LIU Wenjie, WEI Jianan, JIN Shuanggen, LIU Jingnan
- VLBI和GPS观测联合解算地球自转参数和日长变化
- Estimation of Earth Rotation Parameters and ΔLOD with Combining VLBI and GPS Observations
- 武汉大学学报·信息科学版, 2016, 41(1): 66-71,92
- Geomatics and Information Science of Wuhan University, 2016, 41(1): 66-71,92
- http://dx.doi.org/10.13203/j.whugis20130435
-
文章历史
- 收稿日期: 2013-08-24

2. 新南威尔士大学建筑环境学院, 澳大利亚新南威尔士, 2052;
3. 中国科学院上海天文台, 上海, 200030;
4. 武汉大学GNSS中心, 湖北 武汉, 430079
2. Faculty of Built Environment, University of New South Wales, NSW 2052, Australia;
3. Shanghai Astronomical Observatory, Chinese Academy of Sciences, Shanghai 200030, China;
4. GNSS Research Center, Wuhan University, Wuhan 430079, China
高精度地球定向参数(Earth orientation parameter,EOP)是地球参考框架和天球参考框架之间相互转换的重要参数,也影响时间系统( 协调世界时UTC与世界时UT1) 的相互转换,在飞行器的精密定位和导航方面[1, 2]应用广泛并且包含了丰富的地球动力学信息。目前主要利用甚长基线干涉测量(very long baseline intergerometrh,VLBI)观测数据解算EOP,精度高且稳定性强[3],但是测站较少且不连续;而全球定位系统(GPS)数据能够解算地球自转参数,在GPS测站很多且分布较为理想的情况下,其解算精度可以与VLBI解算精度相当。GPS技术能够提供高精度、高分辨率的地球自转参数(Earth rotation parameter,ERP) 序列值,有效地弥补了VLBI技术观测密度不够的缺陷,但是,GPS解算地球自转参数的稳定性有待提高。联合GPS和VLBI技术解算地球自转参数能较好地利用两者的优势,弥补互相的不足,有望获得精度高和稳定性好的ERP和日长变化解算结果。
1 GPS与VLBI解算原理 1.1 GPS估计地球自转参数基本原理采用双差模型解算地球自转参数[4, 5],待估参数为站坐标、卫星坐标、地球自转参数和中性大气延迟。GPS载波相位观测值表示为待估参数的函数模型:
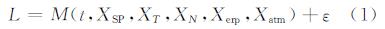
式中,M表示观测量与待估参数的函数模型;t为时间;XSP为初始时刻的轨道根数和摄动参数(辐射压模型);XT为测站坐标;XN为相位模糊度;Xerp为地球自转参数;Xatm为大气延迟;ε为观测噪声。
将式(1)线性化为:
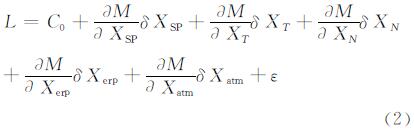
式中,C0表示由近似参数计算出的理论观测值。地球自转参数偏导数可表示为:
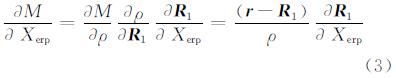
式中,r和R1分别表示为卫星和测站在惯性坐标系中的位置矢量;ρ为站星之间的距离;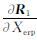 分别包括
分别包括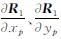 和
和 3部分,xp和yp表示极移在x、y方向的分量,DR表示UT1-TAI的一阶变化率。
3部分,xp和yp表示极移在x、y方向的分量,DR表示UT1-TAI的一阶变化率。
计算星间距离ρ时,卫星及接收机的位置矢量要换算到同一坐标系下,通常为天球参考系统ICRS。但是,接收机的坐标一般都是在国际地球参考系统ITRS下给出的。所以需要将ITRS转换到ICRS下,其转换关系为R(ti)=PNSWR0i。其中,P、N为岁差、章动旋转矩阵,S为地球自转矩阵,W为极移矩阵。
其中,站坐标与卫星轨道参数来自IGS结果。通过以上解算,可求出地球自转参数信息。
通常用日长(length of day,LOD)的观测值相对于标准日长(86 400国际时秒)的变化ΔLOD来表示地球自转速率的变化[6]。通过对GPS观测量进行解算便可得到相应的UT1-TAI。ΔLOD的计算方法为:
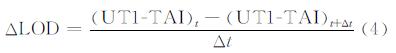
设VLBI的基本观测方程为:
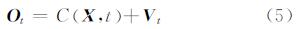
式中,Ot是在t时刻获得的时间延迟和延迟率观测量;X是由与观测量有关的参数组成的向量;C(X,t)为参数X对观测量Ot影响的数学模型,也是观测量的理论值;Vt是观测量的噪声残差向量。
设参数X由先验值X0和改正值x两部分组成,则将观测方程线性化有:

由式(6)整理得线性化观测方程为:
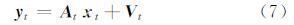
式中,yt=Ot-C(X,t),是t时刻观测值与理论值之差;At为偏导系数矩阵,它与参数值相对于观测值的变化有关。
若将观测方程用矩阵形式表示,则有:

并设观测权阵为P,则根据最小二乘理论可求接触参数的修正值为:

利用卡尔曼滤波进行VLBI大地测量的参数解算[8]时,将用随机模型取代钟和大气延迟的多项式参数模型,对于非随机参数随机扰动矢量为零,这些参数包括台站位置、射电源坐标和地球定向参数等,而随机参数则包括用于表示钟和大气延迟扰动的随机过程分量。
2 数据处理对GPS和VLBI的解算结果进行联合,需要选取GPS和VLBI同一观测时间段,经过对比,本文选取了2005年9月和2006年1、2月的数据。在GPS方面,为了获得较好的精度而采用了24 h观测资料来进行求解。本文选取了全球均匀分布、几何结构良好、相对稳定的17个IGS站(具体测站名见表 1)的观测数据来解算地球自转参数。VLBI方面,本文选择国际上通用的X波段(波长约为3.6 cm)中观测精度较高的XA和XE两种类型观测数据进行分析。
| 测站类型 | 测站名 |
IGS核心站 |
ALGO、ALIC、AUCK、BJFS、BRAZ、DAGR、FAIR、GRAZ、HRAO、KELY、KIT3、KOKB、OHI2、SANT、SYOG、TIXI、YE LL |
GAMIT解算地球自转参数时,大部分的参数设置为默认值,详见文献[9]。
用标准均方根NRMS的大小来评定解算结果,一般为0.25左右。若大于0.5,表明处理结果有问题,需要重新处理基线;若NRMS小于0.5,则认为解算成功。本文解算的NRMS均在0.18~0.25范围内。最后得到的ERP和ΔLOD是每天UTC12:00:00的参数值,将其与IGS结果进行对比来评定外符合精度。差值见图1。

|
| 图 1 GPS解算值与IGS结果比较 Fig. 1 Comparation of GPS-Estimated ERP and ΔLOD to IGS Solutions |
计算得出极移在X与Y方向上的分量与IGS结果比较的均方根分别为0.32 mas与0.28 mas,UT1-UTC和ΔLOD的均方根分别为0.029 ms和0.044 ms/d。
对2006年的解算结果先去除趋势项,然后进行频谱分析,发现极移在X方向与Y方向上的分量、UT1-UTC和ΔLOD存在周期项,分别在14 d和7 d左右。考虑到IGS是采用周解的方式得到结果,故与其做差后的差值序列会有相应的周期项。
2.2 VLBI数据处理及分析本文用OCCAM 6.2处理IVS服务器上相同时段的XA、XE类型的NGS数据,为了与GAMIT保持一致,选择MHB2000章动模型。将解算结果与IVS结果进行比较,差值见图2。用差值的均方根来评定外符和精度,计算得VLBI数据解算结果与IVS结果的差值在极移X方向与Y方向上的均方根分别为0.45 mas与0.58 mas,UT1-UTC和ΔLOD的均方根分别为0.020 ms和0.059 ms/d。
2.3 基于内符合精度的加权平均先用三次拉格朗日插值对GPS和VLBI的解算结果进行插值,得到与IERS 08C04相同历元的ERP和ΔLOD序列;再根据误差传播定律,利用解算结果的中误差分别求出VLBI和GPS解算结果插值后序列的中误差;再以此中误差平方的倒数为权做加权平均,公见如下:
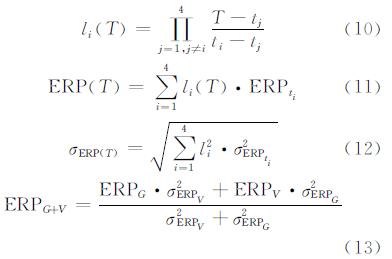

式中,li 为拉格朗日插值多项式的系数;t表示解算结果对应的历元;ERPt 表示解算结果序列;σERPt表示ERPt的中误差;T表示IERS08C04公布值的历元;ERP(T)表示插值后的序列;σERP(T)为插值后的序列的中误差;ERPG和ERPV分别表示利用GPS和VLBI结果插值后的序列;ERPG+V表示加权平均后的序列;ERPIERS表示IERS 08C04序列;RMSG+V表示加权平均后序列与IERS 08C04公布值的均方差。计算结果见表2。
| 解算数据源 | GPS | VLBI | 加权平均 |
| RMS_Xp/mas | 0.33 | 0.60 | 0.46 |
| RMS_Yp/mas | 0.30 | 0.64 | 0.44 |
| RMS_UT1-UTC/ms | 0.011 | 0.141 | 0.140 |
| RMS_ΔLOD/(ms\5d-1) | 0.049 | 0.113 | 0.101 |
加权平均后的均方根均位于两者之间,UT1-UTC和ΔLOD的均方根比较靠近VLBI结果的均方根,是由于VLBI的解算结果精度高、权重大。
2.4 基于IERS 08C04序列的加权平均将2005年9月以及2006年1月、2月IERS 08C04的结果和VLBI的解算结果采用分段三次厄米多项式插值得到每天UTC12:00:00的参数值,再计算GPS解算结果和VLBI解算结果与IERS 08C04结果相比较的均方根,以均方根的平方的倒数作为权进行加权平均,公式如下:
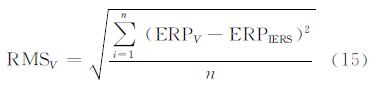

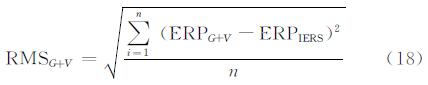
式中,ERPG、ERPV和ERPG+V分别表示利用GPS和VLBI结果插值后的序列及加权平均后的序列;RMSV、RMSG和RMSG+V分别表示以上序列与ERPIERS的均方根。计算后具体的差值见图3。

|
| 图 3 单独解算与加权平均后ERP和ΔLOD与IERS 08C04比较 Fig. 3 Comparison of ERP and ΔLOD Estimated from VLBI and GPS and GPS + VLBI Combined Solutions to IERS 08C04 |
最终计算得极移在X方向与Y方向上的分量与IERS 08C04公布值的均方根(见表3)。由表3的数据可以看出,经过加权平均后,极移在X方向上的分量Xp、极移在Y方向上的分量Yp、日长变化ΔLOD各参数的均方根(RMS_Xp、RMS_Yp、RMS_ΔLOD)有所下降,UT1-UTC的均方根(RMS_UT1-UTC)相当,总的来说, 两者联合提高了解算结果的可靠性,而且与IERS 08C04公布值的差值的波动也更加平稳,即解算结果的稳定性也有所提高。
| 解算数据源 | GPS | VLBI | 加权平均 |
| RMS_Xp/mas | 0.31 | 0.46 | 0.28 |
| RMS_Yp/mas | 0.29 | 0.59 | 0.28 |
| RMS_UT1-UTC/ms | 0.013 | 0.123 | 0.017 |
| RMS_ΔLOD/(ms\5d-1) | 0.048 | 0.085 | 0.038 |
本文利用GAMIT软件处理了2005年9月和2006年1月、2月的GPS数据,并用OCCAM 6.2软件处理了同时期的VLBI观测数据,解算的精度较高。 在解算出ERP和ΔLOD的基础上,本文运用分段三次厄米多项式的插值,将IERS 08C04的公布值和VLBI的解算结果插值到与GPS结果相同的时刻,IERS 08C04的数据密度大、精度高,所以插值效果好。VLBI数据的解算结果插值后精度略微有所下降,拉格朗日插值的结果和分段三次厄米多项式插值的结果的均方根差别较大,表明插值方法对其结果有较大影响。
对GPS和VLBI数据的解算结果进行加权平均综合后,ERP和ΔLOD的解算结果与IERS 08C04的公布值对比的均方根变小,差值的波动幅度变小,可靠性和稳定性都有所提高。
| [1] | Wei Erhu, Jin Shuanggen, Yang Hongzhou, et al. Simulation and Results on Real-Time Positioning of Chang'E-3 Rover with the Same-Beam VLBI Observations[J].Planetary and Space Science, 2013,84:20-27 |
| [2] | Wei Erhu, Jin Shuanggen, Zhang Qi, et al. Autonomous Navigation of Mars Probeusing X-ray Pulsars:Modeling and Results[J]. Advances in Space Research, 2013 (5):849-857 |
| [3] | Wei Erhu, Yan Wei, Jin Shuanggen, et al. Improvement of Earth Orientation Parameters Estimate with Chang'E-1 ΔVLBI observations[J]. Journal of Geodynamics, 2013, DOI:10.1016/j.jog.2013.04.001 |
| [4] | He Zhanke,Yang Xuhai, Li Zhigang, et al. Estimation of Earth Rotation Parameters Based on GPS Observations[J]. Journal of Time and Frequency, 2010, 33(1):69-76(何战科,杨旭海.利用GPS观测资料解算地球自转参数[J].时间频率学报,2010,33(1):69-76) |
| [5] | Wei Erhu, Li Guangwen, Chang Liu, et al. On the High-Frequency ERPs with GPS Observations[J]. Geomatics and Information Science of Wuhan University, 2013,38(7):818-821(魏二虎,李广文,畅柳,等.利用GPS观测数据研究高频地球自转参数[J].武汉大学学报·信息科学版,2013,38(7):818-821) |
| [6] | Wei Erhu,Tian Xiaojing,Liu Jingnan,et al. Analysis of the Length of Day with 2008-2009 VLBI Observations[J]. Geomatics and Information Science of Wuhan University, 2010,35(9):1 009-1 011 (魏二虎,田晓静,刘经南,等.利用2008-2009 年VLBI 数据进行日长变化的研究[J].武汉大学学报·信息科学版,2010,35(9):1 009-1 011) |
| [7] | Li Zhenghang, Wei Erhu, Wang Zhengtao, et al. Space Geodesy[M].Wuhan:Wuhan University Press, 2010:118-158 (李征航,魏二虎,王正涛,等.空间大地测量学[M].武汉:武汉大学出版社,2010:118-158) |
| [8] | Zheng Yong, Yi Zhaohua, Xia Yifei. The Application of Kalman Filtering in Data Processing of VLBI[J]. Acta Astronomica Sinica, 1998,39(2):76-80(郑勇,易照华,夏一飞.卡尔曼滤波在VLBI数据处理中的应用[J].天文学报,1998,39(2):76-80) |
| [9] | Department of Earth, Atmospheric, and Planetary Sciences, Massachusetts Institute of Technology. GAMIT Reference Manual[M]. Massachusetts:Massachusetts Institute of Technology, 2006 |
 2016, Vol. 41
2016, Vol. 41


