文章信息
- 暴景阳, 翟国君, 许军
- BAO Jingyang, ZHAI Guojun, XU Jun
- 海洋垂直基准及转换的技术途径分析
- Vertical Datums and Their Transformation Approaches for Hydrography
- 武汉大学学报·信息科学版, 2016, 41(1): 52-57
- Geomatics and Information Science of Wuhan University, 2016, 41(1): 52-57
- http://dx.doi.org/10.13203/j.whugis20150491
-
文章历史
- 收稿日期: 2015-07-31

2. 海洋测绘研究所, 天津, 300061
2. Institute of Hydrographic Surveying and Charting, Tianjin 300061, China
海洋垂直基准是描述海洋区域及毗邻陆地空间地理信息垂向坐标的参考基准系列,表现为地球椭球面、国家高程基准、深度基准面和净空高度参考面以及平均海面等多种类型[1, 2, 3]。
由于在海洋上不存在水准测量的条件,同时也缺乏对高程信息的需求,因此,依据深度基准面测定和表示水深的分布,以及依据净空参考面确定海面以上某些特征目标的净空高度的技术模式,长期以来为海洋测绘实践所遵循。
陆海一体化测绘技术的发展,GNSS高精度定位技术支持下的无验潮水深测量方法的推广,正推动着海洋地理信息获取与表示的相关理论和技术的变革。作为海洋测绘及相关测绘领域的热点问题之一,国内外近20年来对海洋垂直基准基本体系、垂直基准转换方法进行了较深入的研究。文献[4]在对垂直基准研究论证的基础上,起草了FIG专题指南,文献[5]研究了陆海基准转换与陆海地形统一问题。近10年来,正逐步实现垂直基准转换的工程化。文献[6, 7, 8]分别就局部海域和感潮河段的深度基准模型构建、远海GNSS潮汐观测技术下的垂直基准转换等进行了实验研究。文献[1, 2, 9, 10, 11, 12]对验潮站深度基准确定、基准确定所需的调和常数精度以及海洋测绘垂直基准体系进行了系列研究。
本文对海洋垂直基准所涉及多种基准面的含义,验潮站对垂直基准的维持和控制作用,不同垂直基准面相互转换的方法及精度进行了分析讨论。
1 海洋多垂直基准及转换方法海洋垂直基准包括地球椭球面、国家高程基准、深度基准面和净空高度参考面等多种选择。验潮站是垂直基准的观测设施,由验潮站水位观测数据的分析计算可以得到与水位记录零点相关的潮汐基准信息,进而通过验潮站大地联测数据实现与高程基准的联系,反映离散验潮站点的垂直基准转换关系。
1.1 水位观测结果描述的基准信息无论采用水尺还是其他现代技术实施水位观测,由验潮站测定的水位序列均以验潮站记录零点为参考,相应数据表示于验潮站零点的自由垂直基准。
由观测获得水位序列为wi(i=1,2,…,N),N为序列长度,则由序列平均得平均水位 w。在不计陆海垂直运动的前提下,随着观测序列的增长,潮汐和气象等扰动因素的影响得以滤除,从而平均水位趋于稳定。平均水位一般称为平均海面,是验潮站水位观测结果的重要统计量,也是其他潮汐特征面计算的参考面。
深度基准面和净空高度参考面属于潮汐类型的垂直基准,一般设定为某种类型的特征高潮面和特征低潮面,用做水位归算的参考面,一方面保证基准面的稳定性与信息获取的可再现性,另一方面,使得测定和表示的水深以及空中助航物和碍航物高度具有尽量保守的特性,确保水面舰船活动安全,而又不导致有效航行资源浪费。我国将这两种参考面分别规定为理论最低潮面和平均大潮高潮面。下文仅就深度基准面与高程基准面的关系进行分析讨论。
关于理论最低潮面的计算,文献[10]已做详尽讨论和说明,本文仅给出其原理性定义式:

式中,L为潮汐(潮波)平衡面与最低潮面的垂直距离,即深度基准值;H、g为分潮调和常数;σ为分潮角速率;V0为参考时刻的平衡潮相角;f为分潮交点因子;下标i表示分潮序号。计算采用规定的13个分潮。
综合平均水位和深度基准值,实现深度基准面验潮站记录零点上的定位:

式中,w为根据观测水位序列计算的平均水位;wL为深度基准在水尺上的读数。
1.2 平均海面和深度基准的高程确定在验潮站水准点高程已知,且水尺与其水准联测的前提下,可据式(3)~(6)分别确定平均海面与深度基准面的正常高和大地高。

式中,HMSL 和ζ为平均海面高程,即海面地形高度;HMSL 为平均海面大地高;HL和hL分别为深度基准面的正常高与大地高;Hmark和hmark分别表示验潮站水准点的正常高和大地高;h0-mark为水尺零点与水准点之间的高差。
式(3)提供了由验潮站水位观测及基准联测数据确定平均海面高程,即海面地形的实测方法,式(4)给出了平均海面大地高的实测原理。两式的结果分别可为海面地形模型和平均海面高模型提供精度检核与模型修正的控制信息。式(5)则用于实现深度基准面在国家高程基准中的定位,实质上给出验潮站点深度基准和高程基准,以及验潮站邻域内深度数据和高程数据的转换关系。由式(6)确定的深度基准面大地高可应用于深度基准面分离模型[3, 4]的检核与控制。
1.3 垂直基准转换的技术途径1) 途径1:根据验潮站观测信息实施基准转换。这种转换根据验潮站处的水准联测数据直接利用公式计算,是常规海洋测绘沿岸地形测量和水深测量成果的相互校核方法,在传统应用中通常不做垂直基准统一,仅适用于验潮站的有效作用范围。
2) 途径2:根据多个离散的验潮站形成的基准关系,对深度基准的大地高数值空间内插,获得所需点的垂直基准转换信息[3]。在我国,由于确定深度基准验潮站基准的计算年代不同,数据观测长度不同,也存在算法差异。因此,深度基准的理论最低潮面含义缺乏一致性,也难以构造连续的转换模型。
3) 途径3:利用海洋潮汐、平均海面高、大地水准面、海面地形等系列模型构建海域不同垂直基准的转换关系模型。最基本的工作是利用潮汐模型按式(1)计算深度基准面的网格模型。在平均海面高模型的支持下,利用式(7)获得深度基准面的大地高模型。
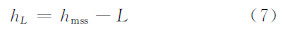
式中,hmss为平均海面高模型的大地高。
确定深度基准面的正(常)模型,即构建深度基准与高程基准间的转换模型,可分别采用式(8)和式(9)两个理论上等价的公式:
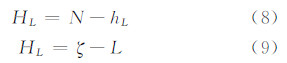
式中,N为大地水准面高,在海域同样视为高程异常;ζ为海面地形高度。
2 验潮站垂直基准确定精度分析验潮站垂直基准的确定涉及基于水位观测数据的平均水位计算、调和分析及深度基准面计算,也决定于基准联测。本文主要根据中国沿岸具有代表性的长期验潮站数据,分析平均水位和深度基准面计算精度与观测时长的关系。
2.1 平均水位确定精度与观测时长的关系根据中国沿岸8个长期验潮站的实测水位数据,统计不同时间尺度平均水位的变化,参考值取为本站多年(整个观测时段)的平均值。不同的时间尺度(1 mon、0.5 a、1 a、2 a、5 a)平均水位差异的统计信息(差值绝对值最大值、中误差)见表 1。
| cm | |||||||||||
| 验潮站 | 统计时段 | 1 mon | 0.5 a | 1 a | 2 a | 5 a | |||||
| 最大值 | 中误差 | 最大值 | 中误差 | 最大值 | 中误差 | 最大值 | 中误差 | 最大值 | 中误差 | ||
| 烟 台 | 1960~1978 | 47.8 | 18.0 | 27.6 | 11.8 | 10.6 | 4.5 | 8.8 | 3.9 | 5.3 | 3.1 |
| 石臼所 | 1975~1997 | 32.9 | 16.0 | 20.1 | 10.2 | 6.1 | 2.7 | 4.5 | 2.3 | 3.4 | 2.0 |
| 连云港 | 1975~1997 | 41.8 | 16.9 | 23.6 | 11.1 | 10.1 | 4.9 | 9.3 | 4.8 | 6.9 | 4.5 |
| 吕 泗 | 1975~1996 | 32.6 | 14.4 | 19.6 | 8.9 | 7.4 | 3.7 | 5.1 | 3.3 | 4.5 | 3.0 |
| 坎 门 | 1975~1997 | 28.5 | 10.8 | 14.9 | 6.3 | 4.7 | 2.2 | 3.3 | 1.9 | 2.7 | 1.5 |
| 厦 门 | 1954~1997 | 38.9 | 12.1 | 19.2 | 7.1 | 13.9 | 3.7 | 8.7 | 3.0 | 4.3 | 2.4 |
| 汕 尾 | 1975~1997 | 35.4 | 9.8 | 20.7 | 7.8 | 3.8 | 2.0 | 3.0 | 1.5 | 1.7 | 1.3 |
| 闸 坡 | 1975~1997 | 38.0 | 10.9 | 14.2 | 5.7 | 4.4 | 2.5 | 3.8 | 1.9 | 2.3 | 1.3 |
| 北 海 | 1975~1997 | 23.5 | 8.4 | 12.7 | 5.0 | 5.3 | 2.2 | 3.5 | 1.8 | 1.8 | 1.1 |
统计计算表明,当平均水位观测时长达到1 a时,算得的平均水位中误差可控制在5 cm之内,而最大偏差可超过10 cm。当时长大于2 a时,中误差在5 cm以内,最大偏差控制在10 cm以内,而2 a的时间尺度对应于我国海道测量作业对长期验潮站的基本时长规定。可以推算,当观测时长达到国际通行规定的19 a长期验潮站基本观测周期时,不计陆海垂直运动影响,基本可以获得±1~2 cm精度量级的平均水位。当然,短于1 a的水位观测,因受到长周期分潮等作用的影响,平均水位变化存在季节规律性,且存在较大短期气象扰动。这类短期验潮站的平均水位确定,需要根据相邻长期验潮站的同步观测数据实施传递法计算。
2.2 深度基准确定精度与观测时长的关系按由13个主要分潮计算理论最低潮面的计算公式,逐月和逐年计算14个长期验潮站的深度基准值,其中,逐月计算时,长周期分潮取当年的年分析结果。以利用整个观测时段观测数据分析计算的深度基准值为比较基准,L值的统计信息见表 2。
| 验潮站 | 时间/a | 1 mon | 1 a | 2 a | ||||||
| 最小值 | 最大值 | 中误差 | 最小值 | 最大值 | 中误差 | 最小值 | 最大值 | 中误差 | ||
| 老虎滩 | 7 | -8.9 | 10.5 | 4.5 | -2.3 | 4.9 | 2.6 | -1.7 | 1.4 | 1.2 |
| 石臼所 | 23 | -19.9 | 20.7 | 8.1 | -6.7 | 5.2 | 3.2 | -6.0 | 3.8 | 2.8 |
| 连云港 | 23 | -24.9 | 26.1 | 10.1 | -11.0 | 12.0 | 5.9 | -9.7 | 8.9 | 5.5 |
| 吕泗 | 20 | -26.6 | 27.6 | 10.9 | -5.7 | 6.5 | 3.6 | -5.7 | 4.7 | 2.8 |
| 坎门 | 23 | -19.3 | 20.0 | 7.4 | -8.1 | 5.7 | 3.4 | -7.1 | 4.2 | 2.7 |
| 厦门 | 43 | -26.3 | 22.9 | 9.4 | -11.7 | 15.3 | 6.3 | -10.8 | 11.2 | 5.6 |
| 基隆 | 18 | -8.1 | 18.4 | 3.0 | -3.9 | 3.8 | 2.2 | -3.2 | 1.7 | 1.4 |
| 高雄 | 18 | -7.5 | 7.1 | 2.4 | -6.8 | 5.6 | 2.8 | -3.9 | 3.3 | 1.8 |
| 汕尾 | 23 | -11.1 | 15.2 | 4.6 | -5.9 | 5.8 | 3.8 | -4.5 | 4.6 | 2.7 |
| 香港 | 12 | -11.6 | 10.2 | 4.8 | -8.3 | 7.3 | 4.7 | -7.8 | 5.3 | 3.7 |
| 闸坡 | 23 | -7.7 | 8.9 | 3.3 | -7.6 | 8.3 | 4.2 | -5.0 | 5.0 | 2.5 |
| 海口 | 22 | -15.6 | 59.8 | 9.0 | -5.1 | 6.6 | 3.4 | -4.4 | 5.7 | 2.9 |
| 北海 | 23 | -30.1 | 53.8 | 14.6 | -10.1 | 13.4 | 7.1 | -8.9 | 12.3 | 6.7 |
| 东方 | 23 | -17.2 | 30.7 | 7.9 | -6.7 | 7.1 | 4.1 | -5.2 | 6.1 | 3.8 |
根据表 2,对所统计的长期验潮站,由逐月和逐年调和常数序列计算的深度基准面中误差的最大值分别为±14.6 cm和±7.1 cm,而最大差异分别达到59.8 cm和15.3 cm。这表明根据理论最低潮面计算公式的直接计算法不适合短期验潮站的深度基准值确定,而必须依据与长期站同步观测信息的传递方法。由长期验潮站(2 a以上)观测数据计算的深度基准值的中误差均在7 cm以内,14个验潮站中有3站超过5 cm。根据文献[12],主要因为潮差大或潮汐参数存在一定的趋势性变化,应做必要的历元归算或其他精处理。
2.3 验潮站垂直基准联测及主要问题分析考虑到验潮站水准点布设于水位观测设施附近,可以按mm级的精度水平实施验潮站零点和水准点之间的水准联测,因此,对于验潮站垂直基准与相关高程系的联系而言,式(3)~式(6)中的水准联测误差可忽略不计。GNSS精密观测给出的大地高观测结果与时长达到19 a的长期验潮站平均水位确定处于大体相当的精度水平。故对于长期验潮站,平均海面和深度基准面的高程及大地高可以在cm级精度水平予以测定。
目前,我国关于验潮站处海面地形和深度基准面确定的主要问题是所依据的高程系统不统一,主要表现在:各长期验潮站的平均海面高程未归化于统一的高程系,分别存在以1956黄海平均海面和1985国家高程基准表示的平均海面高程,甚至存在表示于吴淞零点上的高程。另外,即便与1985高程基准实施水准联测的验潮站,所联入国家水准网点的等级不同,所用高程数据未必是统一的平差成果。因此,由长期验潮站得到的海面地形实测信息不能足够合理地反映海面地形沿海岸的变化情况。图 1是中国沿岸48个长期验潮站现有海面地形实测值随纬度的变化情况。由图 1可见,海面地形数据在20°N附近及国家水准原点以北均存在不够合理的抖动现象。

|
| 图 1 现有长期验潮站实测海面地形高度与测站纬度的关系 Fig. 1 Sea Surface Topography Derived from the Long Period Tidal Stations Observations Along the Coast of China |
本文以南海海域为例,给出了深度基准面及转换模型。
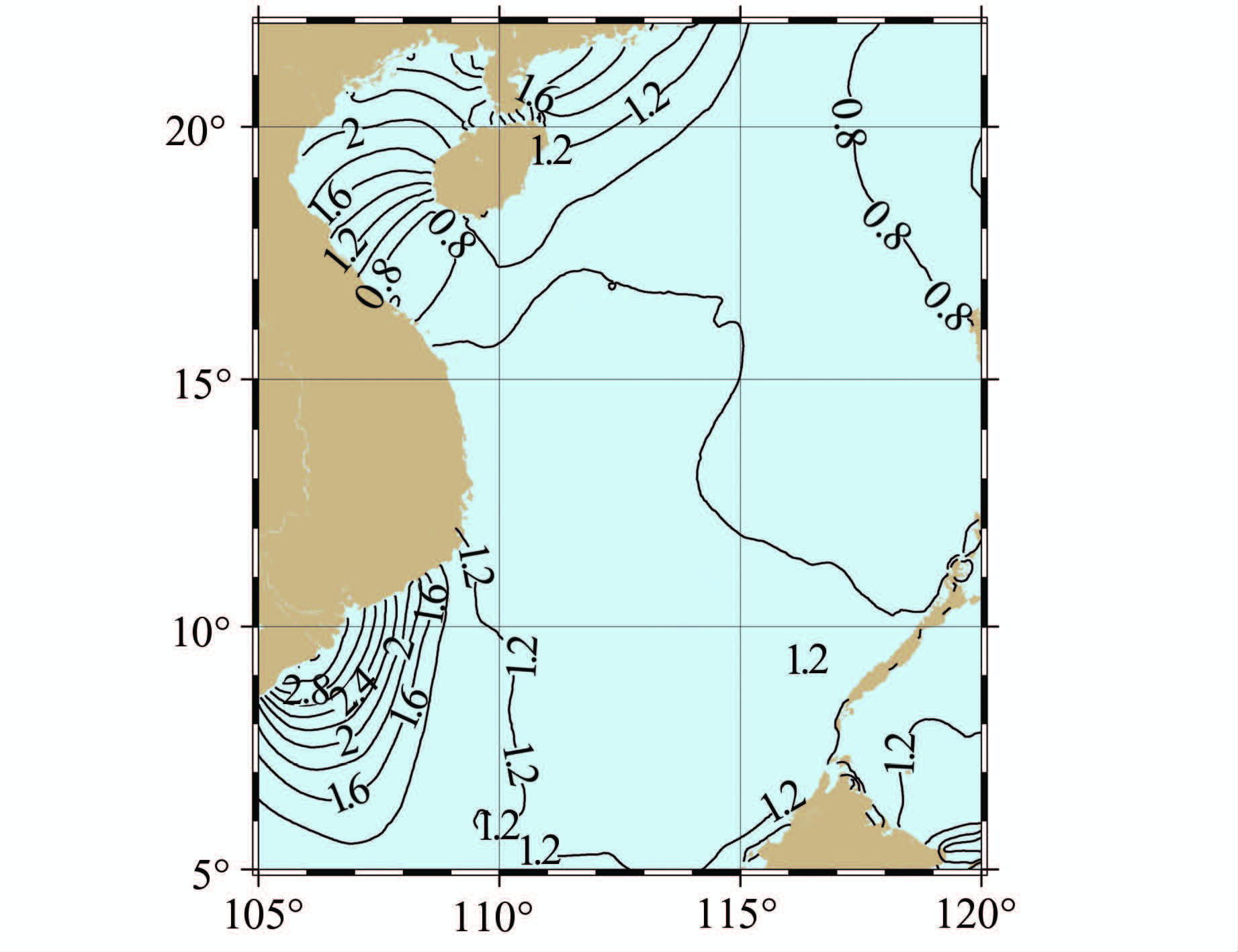
3.1 深度基准面表征的系列模型利用文献[9]潮汐模型,按理论最低潮面的计算公式,计算获得南海深度基准面(L值)模型(见图 2)。覆盖范围为5°N~22°N,105°E~120°E,分辨率5′×5′。图 2中等值线注记单位为m。
|
| 图 2 南海深度基准面模型 Fig. 2 Chart Datum over the South China Sea |
由图 2可以看出,在南海开阔海域,深度基准面相对平均海面变化缓慢且规律性较强,随着向沿岸靠近,深度基准面的数值变大,且呈现出较大的变化梯度,与主要分潮的潮波特征相吻合。
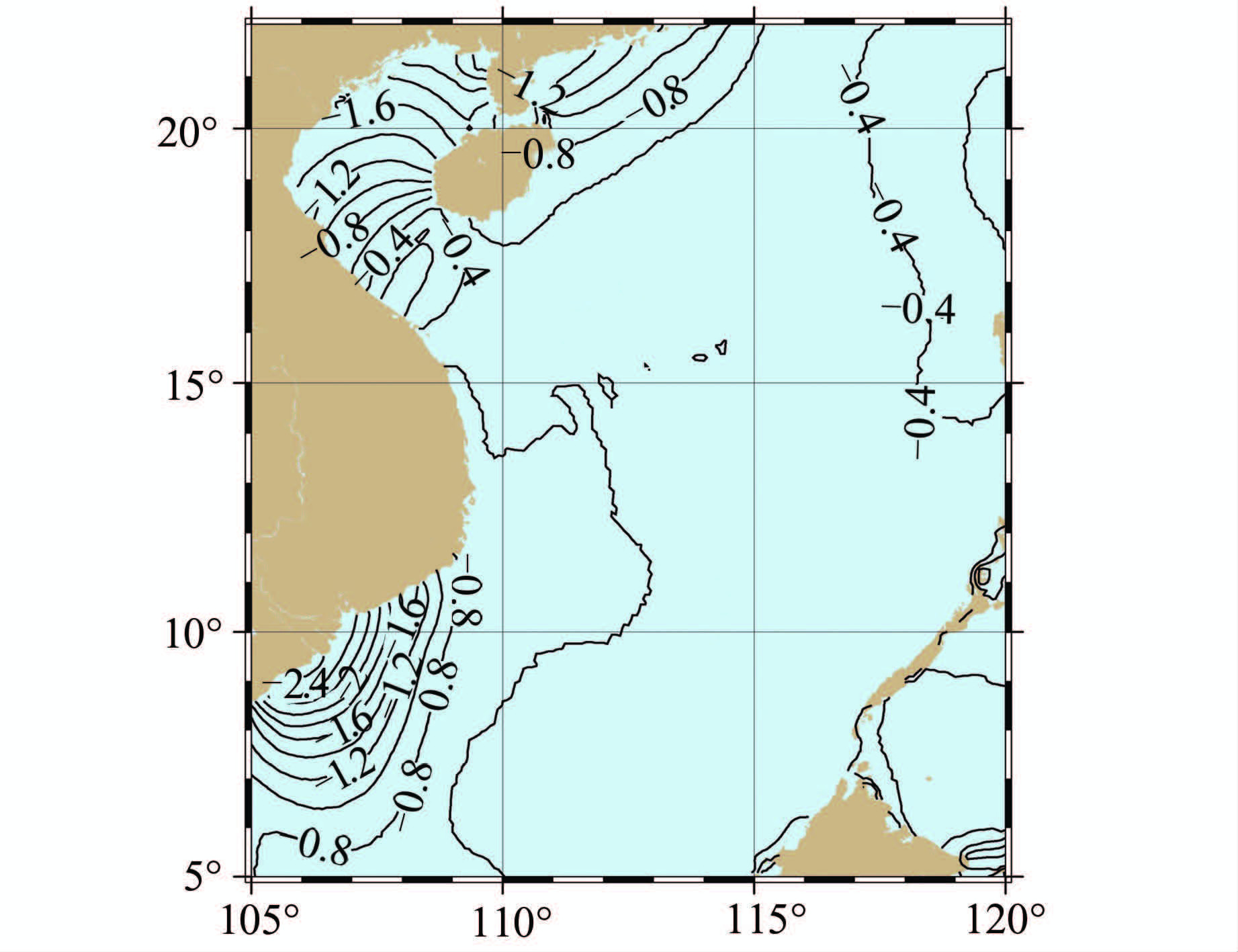
根据式(7)与式(9),分别计算生成南海深度基准面大地高和正常高模型(见图 3和图 4),图 3、图 4中等值线注记单位为m。
|
| 图 3 南海深度基准面正常高模型 Fig. 3 Separation of Chart Datum from Height Datum |

|
| 图 4 南海深度基准面大地高模型 Fig. 4 v |
根据潮汐模型计算深度基准面的精度主要取决于潮汐模型的精度,在开阔海洋区域,全球潮汐模型中主要分潮的综合误差可达2~3 cm,深度基准面模型的确定基本在相同精度量级。而在近海和沿岸区域,潮汐模型及由此计算的深度基准面模型精度会明显降低。当然,由于用于模型精度检测验潮站的代表性不强,由沿岸长期验潮站实测数据对潮汐模型的精度评估应是较为保守的。根据图 2的数据,计算得深度基准面与4个最主要分潮振幅总和的比值介于0.8~1.2之间,采用中国近海潮汐模型[9],计算4个主要分潮综合误差为10.8 cm,按文献[2]提出的深度基准精度估计方法,可估算深度基准面模型的中误差优于±13 cm。
对于沿岸和近海区域,仅由长期验潮站提供的深度基准及大地联测信息控制深度基准面及转换关系模型,数据仍不够充分。一方面,长期验潮站的基准信息不够完备和精确,需要按海洋垂直基准基础设施的建设目标,以尽量长时段的观测数据开展平均海面、深度基准面和其他特征潮面的更新计算,实施统一的大地联测,提供统一系统或框架的平均海面正常高和大地高系统。将短期、临时验潮站与长期验潮站通过同步观测信息,构建垂直基准控制网,实施整个基准网垂直基准信息的综合确定和精度评价,为垂直基准面相关模型系列提供检核和控制依据。
4 结 语本文分析了不同海洋垂直基准面的含义及相互转换关系,特别是深度基准面在高程基准和地球椭球面上表示的实现途径,并利用长期验潮站观测数据验证了不同时段平均水位和深度基准的确定精度水平。以南海为例,本文构建了深度基准面(L值)的模型、正常高模型和大地高模型。分析表明,现有长期验潮站的基准信息尚不能以足够的准确性为海洋垂直基准转换模型提供基础数据支持。按照海洋垂直基准基础设施的建设目标,加强大地联测,开展深度基准面和其他特征潮面的更新计算,并表示于正常高系统和大地高系统的高程基准,进一步控制短期验潮站,形成海域垂直基准控制网,控制海域垂直基准模型,将是基础性和系统性工程。
| [1] | Bao Jingyang, Xu Jun, Cui Yang. Expression and Maintenance of Seamless Vertical Datum for Hydrography[J]. Hydrographic Surveying and Charting,2013,33(2):1-5(暴景阳,许军,崔杨.海域无缝垂直基准面表征和维持体系论证[J]. 海洋测绘, 2013,33(2):1-5) |
| [2] | Bao Jingyang. On the Study of Vertical Datum for Hydrography and Cartography[J]. Hyrographic Surveying and Charting,2009,29(2):70-77(暴景阳. 海洋测绘垂直基准综论[J]. 海洋测绘, 2009,29(2):70-77) |
| [3] | Adams R. Seamless Data and Vertical Datums Reconciling Chart Datum with a Global Reference Frame[J]. Hydrographic Journal,2004,113:9-14 |
| [4] | International Federation of Surveyors. FIG Guide on the Development of a Vertical Reference Surface for Hydrography[R]. FIG Special Publication No.37, FIG, New York, 2006 |
| [5] | Andreasen C.Vertical Datum Issues for Data Continuity from the Land to the Seafloor[C].The Canadian Hydrographic Conference and Natianal Surveyors Conference, Canada, 2008 |
| [6] | Zhao Jianhu, Zhang Hongmei, Clarke J E H. Establishment of Local Seamless Vertical Datum[J]. Geomatics and Information Science of Wuhan University, 2006,31(5):448-450(赵建虎,张红梅,Clarke J E H. 局部无缝垂直参考面的建立方法研究[J]. 武汉大学学报·信息科学版,2006,31(5):448-450) |
| [7] | Zhao Jianhu, Dong Jiang, Ke Hao, et al. High Precision GPS Tide Measurement Method in a Far-Distance and Transformation Model for the Vertical Datum[J]. Geomatics and Information Science of Wuhan University, 2015,40(6):761-766(赵建虎,董江,柯灏,等. 远距离高精度GPS潮汐观测及垂直基准转换研究[J]. 武汉大学学报·信息科学版,2015,40(6):761-766) |
| [8] | Ke Hao, Li Fei, Zhao Jianhu, et al. A Chart Datum Transfer Precision Model in the Yangtze River Estuary Based on Tidal Nature Similarity[J]. Geomatics and Information Science of Wuhan University, 2015,40(6):767-771(柯灏,李斐,赵建虎,等.利用潮汐性质相似的长江口水域深度基准面传递精度研究[J]. 武汉大学学报·信息科学版,2015,40(6):767-771) |
| [9] | Bao Jingyang, Xu Jun. Tide Analysis from Altimeter Data and the Establishment and Application of Tide Model[M]. Beijing:Surveying and Mapping Press,2013(暴景阳,许军. 卫星测高数据的潮汐提取与建模应用[M].北京:测绘出版社,2013) |
| [10] | Bao Jingyang, Liu Yanchun, Chao Dingbo,et al. Computations and Analyses of Chart Datum to Coastal Tide Gauges of China[J]. Geomatics and Information Science of Wuhan University, 2006,31(3):224-228(中国沿岸主要验潮站海图深度基准面的计算与分析[J]. 武汉大学学报·信息科学版,2006,31(3):224-228) |
| [11] | Bao Jingyang, Xu Jun. The Accuracy Evaluation of Harmonic Constants for Long Term Tidal Station Along the Coast of China[J]. Hydrographic Surveying and Charting,2013,33(1):1-4(暴景阳,许军. 中国沿岸验潮站潮汐调和常数的精度评估[J]. 海洋测绘, 2013,33(1):1-4) |
| [12] | Bao Jingyang, Xu Jun, Cui Yang. The Variation and Epoch Correction of Harmonic Constants and Chart Datum[J]. Hydrographic Surveying and Charting,2013,33(3):1-5(暴景阳,许军,崔杨. 调和常数及深度基准面的变化与历元订正[J]. 海洋测绘, 2013,33(3):1-5) |
 2016, Vol. 41
2016, Vol. 41


