2016, Vol. 41文章信息
- 许才军, 邓长勇, 周力璇
- XU Caijun, DENG Changyong, ZHOU Lixuan
- 利用方差分量估计的地震同震滑动分布反演
- Coseismic Slip Distribution Inversion Method Based on the Variance Component Estimation
- 武汉大学学报·信息科学版, 2016, 41(1): 37-44
- Geomatics and Information Science of Wuhan University, 2016, 41(1): 37-44
- http://dx.doi.org/10.13203/j.whugis20150500
-
文章历史
- 收稿日期: 2015-08-14
2. 地球空间环境与大地测量教育部重点实验室, 湖北 武汉, 430079;
3. 地球空间信息技术协同创新中心, 湖北 武汉, 430079
2. Key Laboratory of Geospace Environment and Geodesy, Ministry of Education, Wuhan 430079, China;
3. Collaborative Innovation Center of Geospatial Technology, Wuhan 430079, China
大地测量反演是大地测量学科深入地球科学研究领域的核心手段，利用大地测量资料反演地震机制是地学领域的前沿研究热点。大地测量反演，或者说大地测量地球物理联合反演经历了由单一大地测量数据反演发展到多种大地测量数据以及多类观测数据(包括大地测量、地球物理和地质等数据)参与的联合反演过程；反演模型由最初的连续型发展到离散型，再到时序分析；反演算法，通常根据模型参数与观测数据之间的关系，选择线性或者非线性反演方法以及线性非线性反演[1, 2, 3, 4, 5]。文献[6]推导了全贝叶斯反演方法，并将该方法应用于1999年台湾集集地震同震滑动分布反演，这种方法可以在多种数据相对权重未知的情况下，同时求出滑动分布、平滑因子以及各类数据的相对权比，但该方法非常复杂，计算时间也非常长。文献[7]又在全贝叶斯方法的基础上进行改进，把断层滑动分布反演问题中线性参数和非线性参数分离开，混合使用线性与非线性反演方法(简称F-J方法)，虽然使反演计算效率有较大提高，但反演计算效率仍然很低。
本文采用方差分量估计方法(简称VCE方法)确定地震同震滑动分布反演中平滑因子及各类观测值权比，提高反演效率，并通过对断层滑动分布细节的分析，加深对发震机理和震源破裂过程的认识。
1 方差分量估计方法确定平滑因子的原理地震过程中，地表同震位移与断层滑动量的关系可以表示为：
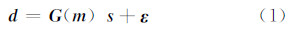
式中，d为观测到的地表形变数据； ε 为随机观测误差； G 是表示模型参数空间到地表形变空间 d 的格林函数，它是断层几何参数的函数； s 是滑动参数。通常可以先通过正演获得与观测数据拟合最佳时的断层破裂几何结构，即先确定断层几何参数 m ，然后再运用式(1) 反演断层滑动分布参数 s ,此时反演属于线性反演。式(1)可以简单地表示为：
如果地表形变观测数据有多类，且相互独立，则式(2)可以表示为：
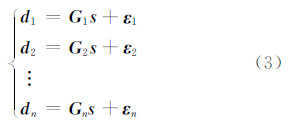
假定将断层面离散为N个断层片，基于位错公式可以计算单位滑动量(包括走向、倾向两个方向)在地表M个观测点产生的地表形变，可以组成一个M×2N大小的系数矩阵(格林函数) G 。由于在反演过程中，将断层面离散化为由上到下排列的均匀或非均匀的小断层片，通常需要对断层片上的位错施加一定的光滑约束条件，以避免滑动分布解的振荡(相邻断层片间的滑动量在大小和方向上存在着显著差异)，其常用方法主要包括一阶差分算子、拉普拉斯算子、三次样条算子等[8]。本文采用拉普拉斯平滑约束，其目的是使得相邻断层片间滑动量的梯度最小[9, 10]。二阶差分算子的拉普拉斯平滑约束数学表达式可写为：
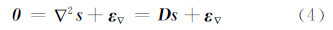
由此地震同震滑动分布反演问题实际上是一个带有约束条件的反演问题，相对于式(3)，式(4)可以看作是一个虚拟观测值方程。
设 d 中包含有n类相互独立的观测数据 d 1,d2,…,dn，其方差协方差阵分别为Σ1,Σ2,…,Σn，则式(3)、式(4)可以使用如下目标函数确定滑动分布参数 s ：
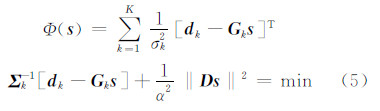
式中，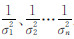
之间的比例关系反映了各类观测数据的权重； 
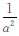表示模型平滑度与数据拟合度之间的相对权比，即平滑因子。
平滑因子表示的是模型平滑度与数据拟合度之间的相对权比，也可以视为一类特殊的权比因子。因为反演问题上可以看成是一个平差问题，使得式(5)中目标函数Φ( s )达到最小的解实际上就是下面观测方程的加权最小二乘解：
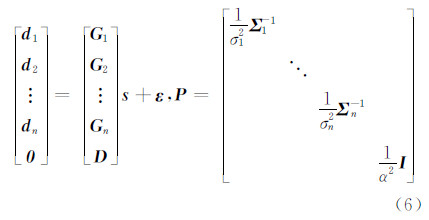
在平差模型式(6)中，函数模型是确定的，随机模型是不确定的。将方程左边的 0 看做虚拟观测值，作为一类观测数据，那么，随机模型中的σi2和α2就是各类观测数据和虚拟观测值的方差分量。对平差模型式(6)采用方差分量估计方法[11, 12]迭代计算，可以求解出各类观测值的方差分量σi2和虚拟观测值的方差分量α2，这就是本文提出的基于方差分量估计方法确定平滑因子的原理。通过确定σi2、α2，最终可以确定滑动分布参数 s ，即反演给出滑动分布量。
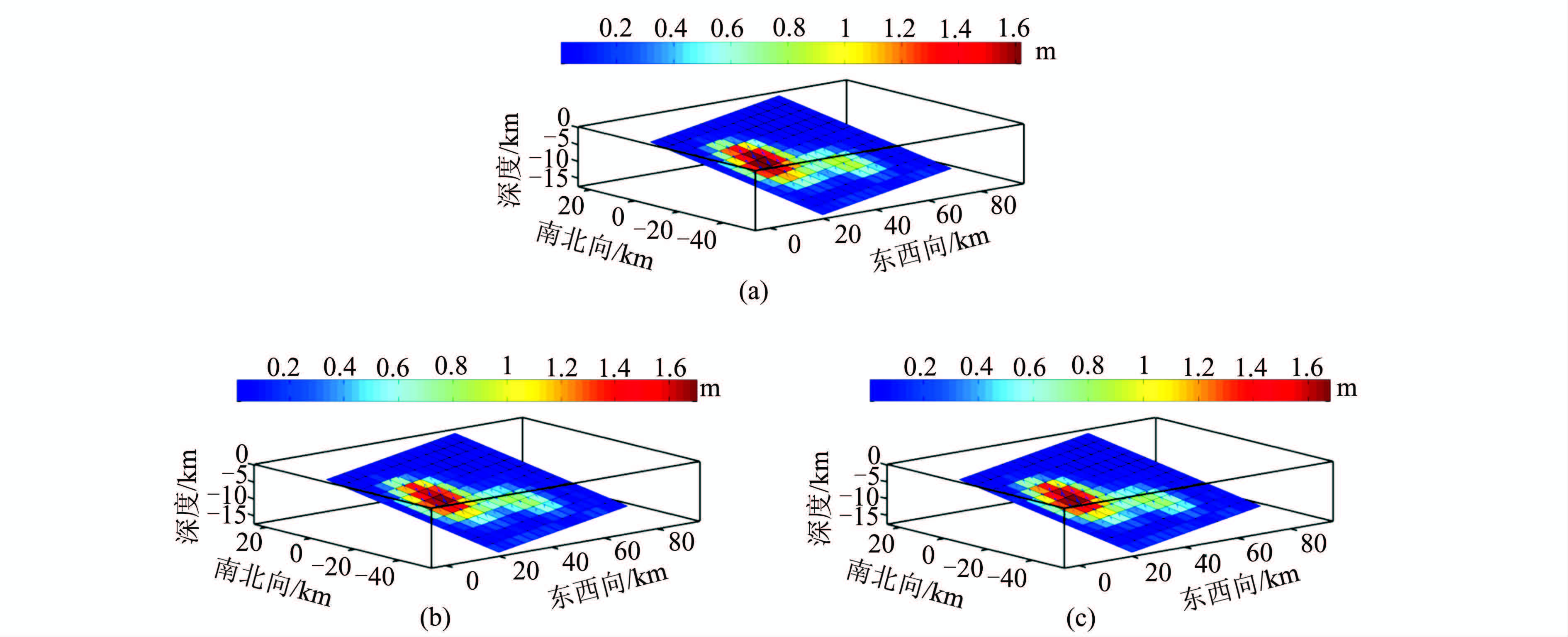
2 模拟算例模拟一个在半无限均匀弹性空间中长度为75 km，宽度为60 km，走向角为70°，倾角为15°的断层。断层的左上角沿深度向的投影在坐标原点，其深度为1 000 m。将断层划分为5 km×5 km的子断层，并在各断层上附加一定的滑动量(图 1(a))，滑移角设定为45°，走向滑动量和倾向滑动量最大均为1.13 m，总的滑动量最大为1.60 m。
|
| 图 1 模拟的滑动分布及反演结果图 Fig. 1 Synthetic Slip Distribution and Inversion Results |
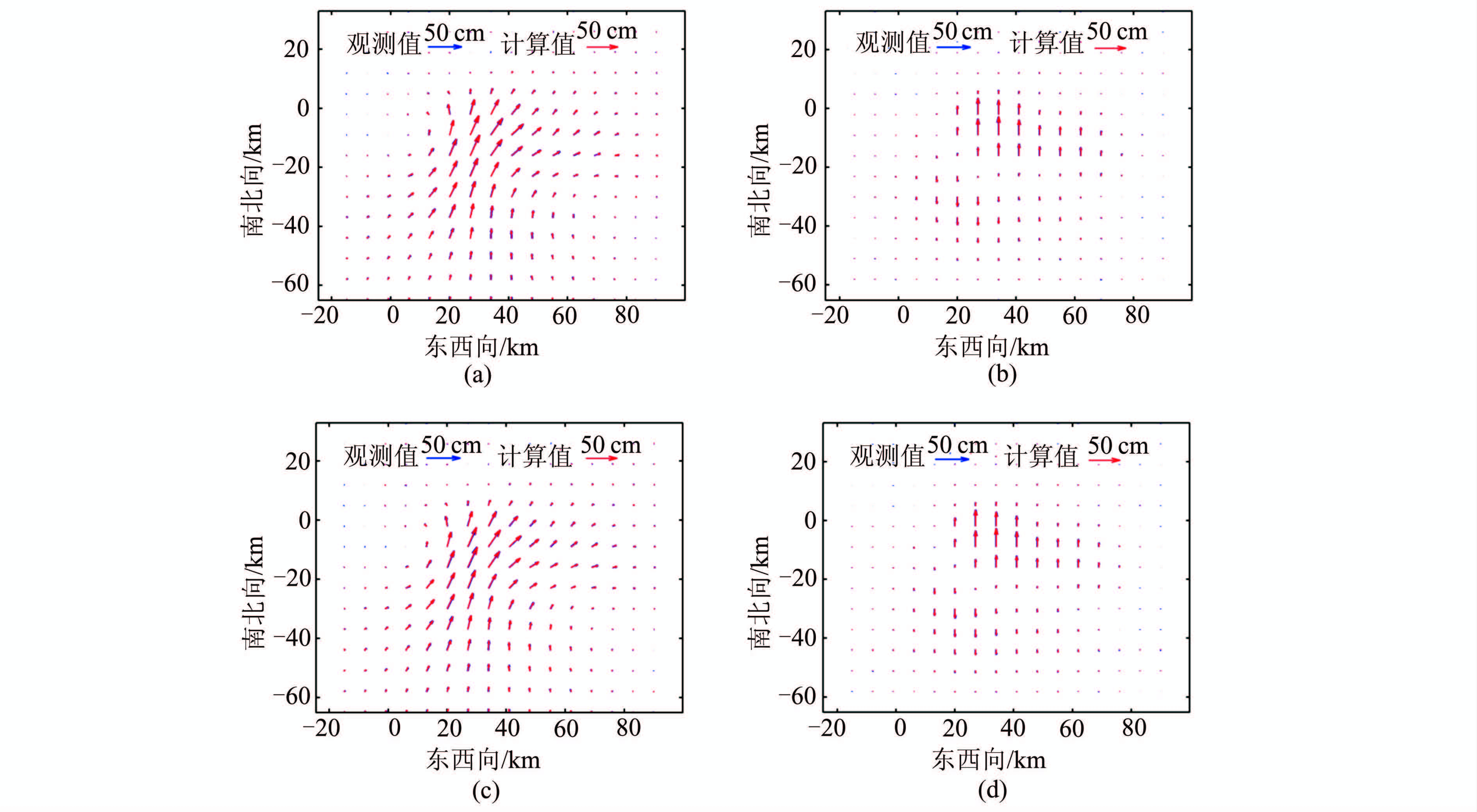
根据上述模拟的断层分布和半无限均匀弹性空间的位错模型[13]，在地表位移中，对水平向位移加入均值为0 mm、方差为32 mm2的高斯白噪声，而垂直向位移中加入均值为0 mm、方差为52mm2的高斯白噪声，计算出均匀分布的240个站点(见图 2)的三维形变量，将水平向的形变量d1作为一组数据，垂直向的形变量d2作为另外一组数据，数据集d2和数据集d2的方差协方差阵分别为Σ1=32 I (480)和Σ2=52 I (240)，从而得到两组精度不同的数据(可以代表GPS水平向或GPS垂直向或INSAR或水准测量值等)。图 2中，蓝色部分为模拟的观测形变量，红色部分为反演所得模型通过正演计算得到的形变量。
|
| 图 2 模拟的观测形变量及反演结果图 Fig. 2 Synthetic Displacement and Inversion Results |
本文采用VCE方法和F-J方法进行反演计算，令σ12=1、σ22=1和α12=1，即VCE方法和F-J方法的相对权比初始值为1∶1∶1。
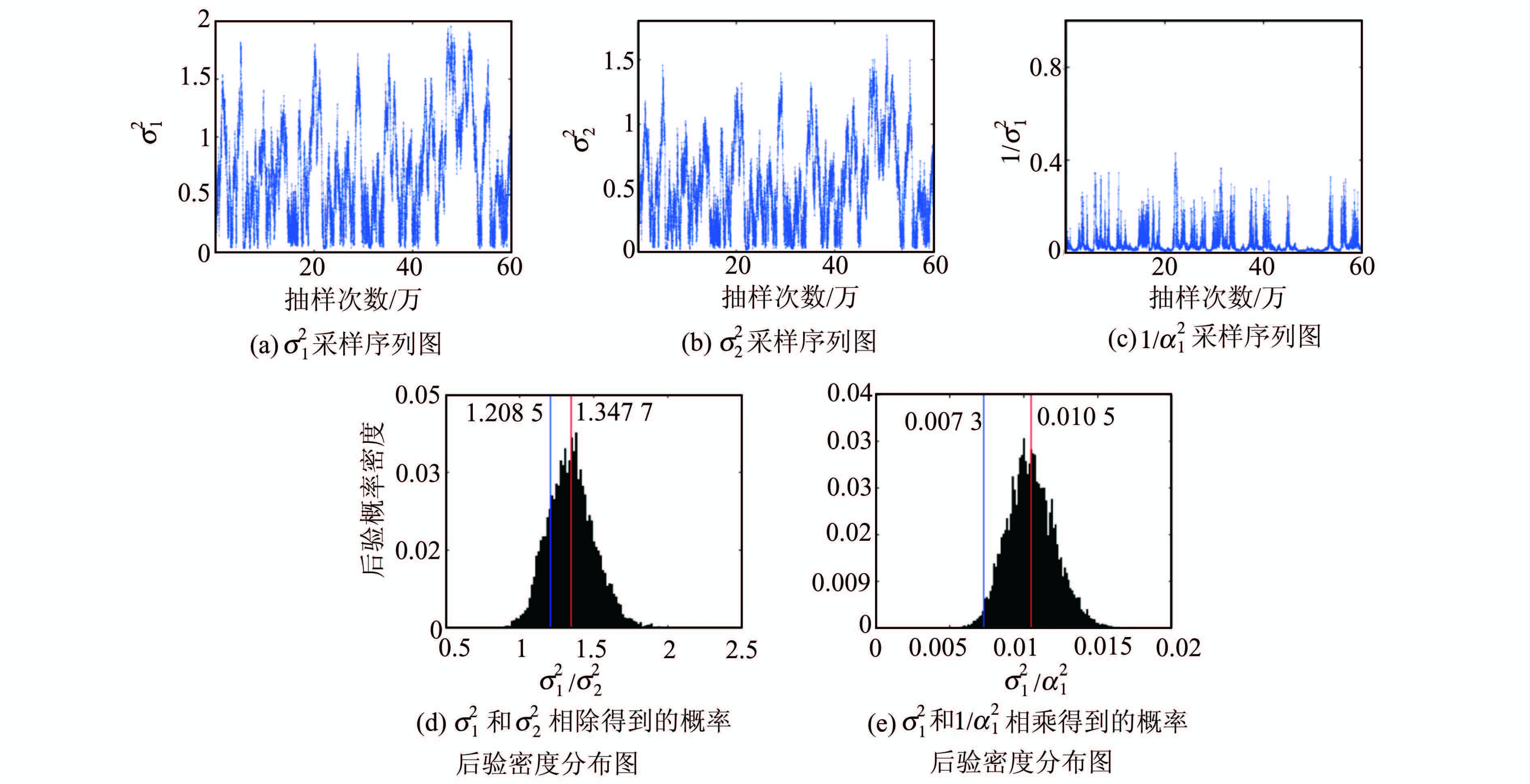
F-J方法的抽样次数为600 000，各超参数σ12、σ22和1/α12的初始值均为1，步长均为0.01。由于F-J方法需要一个预烧期[14]，并且由图 3(a)、图 3(b)和图 3(c)可知，抽样20 000次后，超参数收敛，本文将前面20 000次采样设为预烧期，为了减弱相邻抽样之间的相关性，预烧期后面的抽样每隔10次选取一个作为有效抽样,然后将 有效采样取平均得到超参数值，最终得到各超参数的权比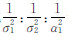 
=1∶1.347 7∶0.010 5。图 3中，红色垂直线坐标值是取采样值的平均值得到的，蓝色垂直线坐标值是VCE方法得到的结果。
|
| 图 3 超参数采样序列图及概率后验密度分布图 Fig. 3 Sample Serials of Hyper-parameters and the Posterior Probability |
此算例中，VCE方法只用了5次迭代(见表 1)就达到了收敛的条件(各类数据集和虚拟观 测值的单位权方差之比为1)，各超参数的相对权比 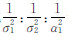=1∶1.208 5∶0.007 3。反演用时仅为40 s，为F-J方法(反演计算用时达到4.0×105 s，约4 d多)的1/10 000。由图 3(d)中可以 看出，VCE方法得到的 
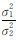和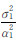 
落在了F-J方法对应的概率后验密度分布内，可以将VCE方法得到结果看作是F-J方法的一个解。两种反演算法得到的滑动分布(图 1(b)、1(c))与模拟的滑动分布(图 1(a))都吻合得很好，F-J方法反演结果与真值之间的最大偏差相对VCE方法的偏差的误差百分比来说要略小，而平均偏差百分比两者几乎相同，两者的误差都在可以接受的范围内(见表 2)。
| 迭代次数 | 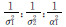 | 数据集d1、d2和虚拟观测值的单位权方差比 |
| 1 | 1∶0.813 7∶0.037 1 | 4.4×10-6∶5.4×10-6∶1.2×10-4 |
| 2 | 1∶1.212 9∶0.008 5 | 0.255 9∶0.171 7∶1.114 6 |
| 3 | 1∶1.214 2∶0.007 4 | 0.897 3∶0.896 3∶1.027 1 |
| 4 | 1∶1.209 4∶0.007 3 | 0.995 3∶0.999 2∶1.010 0 |
| 5 | 1∶1.208 5∶0.007 3 | 0.999 4∶1.001 0∶1.001 0 |
| 方法 | 最大偏差百分比 | 平均偏差百分比 | |
| 走滑 | VCE | 9.81% | 1.69% |
| F-J | 5.42% | 1.67% | |
| 倾滑 | VCE | 5.81% | 1.14% |
| F-J | 3.83% | 1.20% | |
| 总滑动量 | VCE | 7.62% | 1.36% |
| F-J | 3.69% | 1.44% | |
| 计算用时 | VCE 40 s | F-J 4.0×105 s | |
| 注：计算机CPU为Intel Xeon E7430。 | |||
此外，为了定量说明两者反演结果的相似程度，本文采用空间互相关系数[15]来衡量两个滑动分布的相似程度。滑动分布 s 1与滑动分布 s 2之间的空间互相关系数计算公式为：
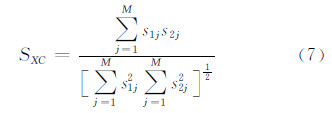
式中，M是滑动分布向量 s 1、 s 2的维数。空间互相关系数的大小可以反映两个滑动分布向量 s 1、 s 2的相似程度。通过计算，VCE方法与F-J方法反演所得的两个滑动分布的互相关系数为0.997。
因此可以说，VCE方法能够得到与F-J(线性非线性反演)方法几乎相同的结果，但前者的运算效率要比后者高得多。
3 Bam地震滑动分布反演 3.1 地表位移数据Bam地震发生于2003年12月26日，当地时间5点56分，格林尼治时间1点56分。欧空局的 Envisat卫星成功获取了此次地震震前、震后升降轨ASAR影像，其中震前影像3幅、震后影像4幅。本文选取的影像对如表 3所示，采用加州理工学院JPL实验室开发的ROI_PAC软件[16]对数据进行干涉处理。在数据处理过程中，结合SRTM[17]提供的地形数据来移除地形的影响，轨道误差采用二次多项式模拟。在模拟轨道误差时，把山体大气也作为轨道误差的一部分加以模拟，计算包含山体大气影响的影像轨道误差。完成整个干涉处理后，就得到了两幅同震形变场，采用四叉树算法对两幅同震形变场进行重采样，一共得到1 022个升轨数据和826个降轨数据，其分布如图 4所示。
| 主影像日期 | 从影像日期 | |
| 升轨 | 2003-06-11 | 2004-02-29 |
| 降轨 | 2003-12-03 | 2004-02-11 |
|
| 图 4 Bam地震中InSAR捕获的地表形变场 Fig. 4 Deformation Field Derived from InSAR in the Bam Earthquake |
本文采用文献[9]给出的单段断层模型进行Bam地震断层滑动分布反演，投影中心为(58.358,29.040),投影公式为通用横轴墨卡托投影，其几何参数见表 4。采用Kada的半无限均匀弹性空间位错模型[13]。
| 分段数 | 经度/(°) | 纬度/(°) | 深度/km | 长度/km | 宽度/km | 走向/(°) | 倾角/(°) |
| 1 | 58.356 | 29.040 | 8.1 | 22 | 19 | 354.6 | 83.8 |
本文采用VCE方法进行反演计算Bam地震同震滑动分布，令σ12=1和α12=1，即相对权比初始值为1∶1。反演结果如图 5所示。
|
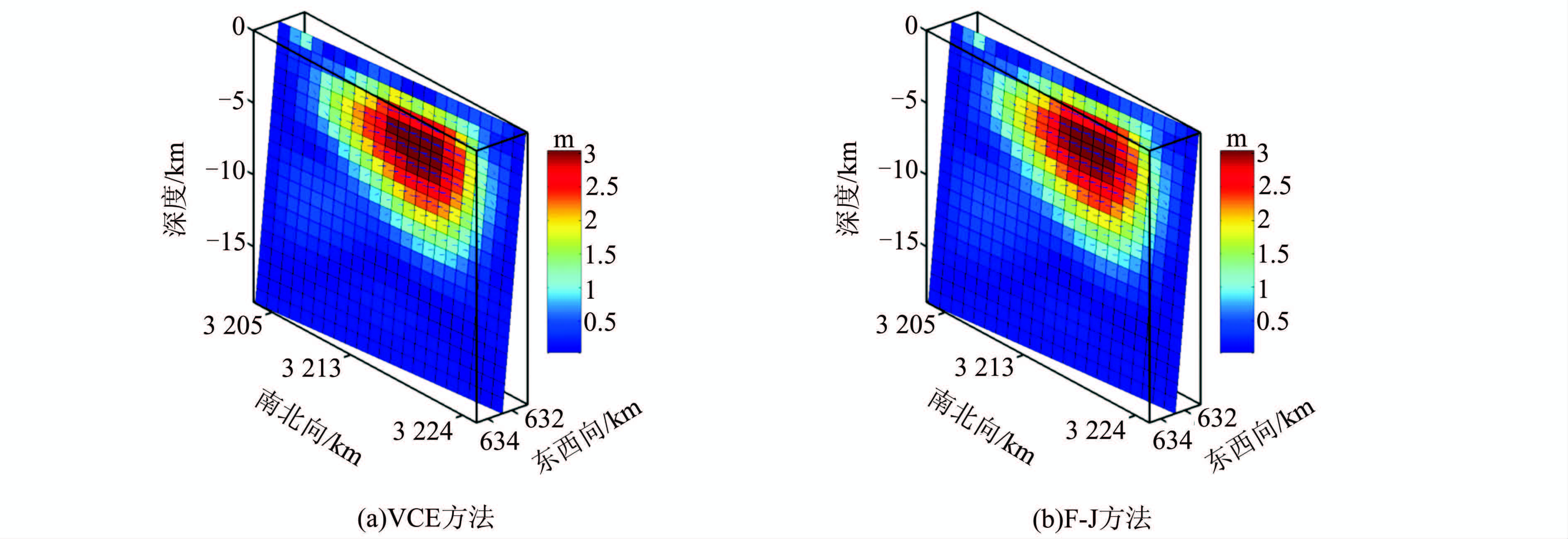
| 图 5 Bam地震同震滑动分布反演结果 Fig. 5 Inversion Results of Coseismic Slip Distribution of Bam Earthquake |
VCE方法只用了13次迭代(见表 5)就达到了收敛的条件，各超参数的相对权比 
=1∶0.000 9。
| 迭代次数 | 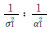 | InSAR数据和虚拟观测值的单位权方差比 |
| 1 | 1∶0.054 8 | 0.001 0∶0.018 6 |
| 2 | 1∶0.013 9 | 0.864 4∶3.400 9 |
| 3 | 1∶0.004 3 | 0.921 4∶3.015 0 |
| 4 | 1∶0.001 9 | 0.945 5∶2.082 7 |
| 5 | 1∶0.001 3 | 0.978 8∶1.462 3 |
| 6 | 1∶0.001 1 | 0.992 1∶1.195 1 |
| 7 | 1∶0.001 0 | 0.996 9∶1.084 8 |
| 8 | 1∶0.000 9 | 0.998 7∶1.038 9 |
| 9 | 1∶0.000 9 | 0.999 3∶1.018 7 |
| 10 | 1∶0.000 9 | 0.999 7∶1.009 0 |
| 11 | 1∶0.000 9 | 0.999 9∶1.004 5 |
| 12 | 1∶0.000 9 | 0.999 9∶1.002 3 |
| 13 | 1∶0.000 9 | 1.000 0∶1.001 1 |
F-J方法的抽样次数为70 000，各超参数σ12和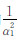 
的初始值均为1，步长均为0.005。将前文5 000次采样设为预烧期(见图 6(a)、6(b))，预烧期后面的抽样每隔10次选取一个作为有效抽样,然后将有效采样取平均得到超参数值，最终得到各超参数的权比 =1∶0.001 3。
|
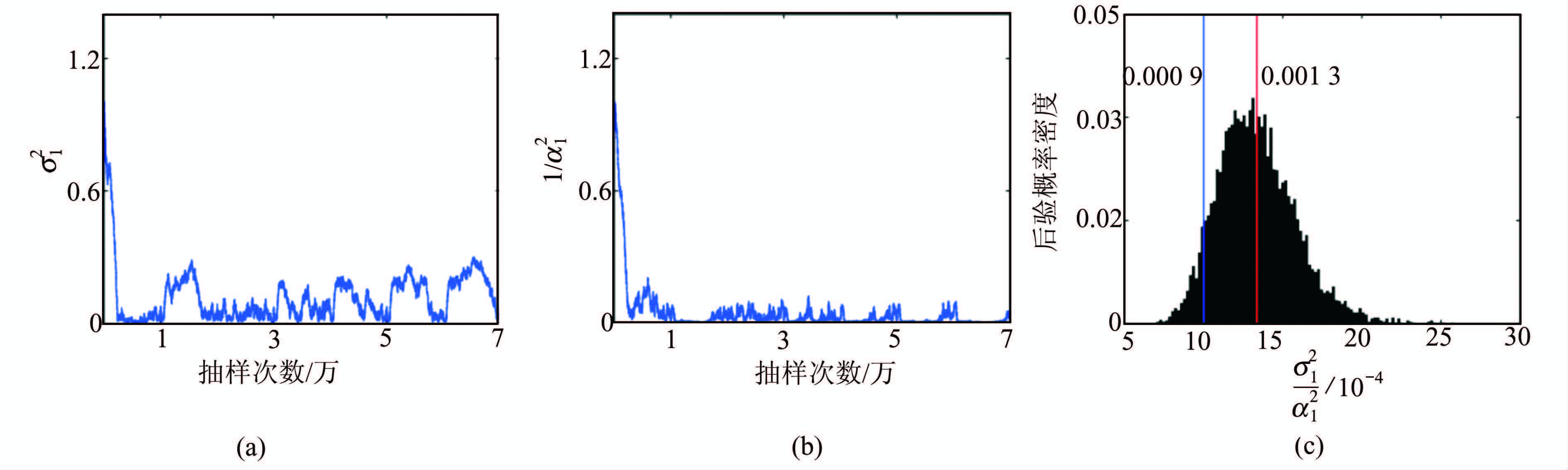
| 图 6 Bam地震超参数采样序列图及概率后验密度分布图 Fig. 6 Statistic Histogram of Hyper-parameters Samples in Bam Earthquake |
VCE方法与F-J方法得到的Bam地震断层滑动分布之间的空间互相关系数为0.999 9。这表明两种反演方法结果之间的一致性非常好。表 6给出了两种方法反演得到的同震滑动分的统计结果。从表 6中可以看出，两者结果几乎相同，由VCE反演Bam地震得到的震级Mw 6.6，和USGS公布的结果一致；InSAR数据的RMS值20 mm与文献[9]的19 mm的结果几乎相同；VCE方法得到的最大滑动量3.04 m在深度为4.50 km处与F-J方法得到的最大滑动量3.04 m在深度为4.47 km处仅有微小差别；但VCE方法的用时仅为F-J方法(反演计算用时达到1.5×106 s，约17 d)用时的1/6 608。
图 6给出了F-J方法得到的Bam地震算例超参数的采样序列图和概率后验密度分布图。图 6 中，红色垂直线坐标值由取采样值的平均值得到，蓝色垂直线坐标值是VCE方法得到的结果。从表 6和图 6可以看出，VCE方法得到的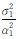 
也落在了F-J方法对应的概率后验密度分布内，表明VCE方法在实际算例中所得结果也是合理的。
| VCE反演方法 | FJ反演方法 | |
| 地震震级/Mw | 6.6 | 6.6 |
| 数据集和平滑矩阵的相对权比 | 1∶0.000 9 | 1∶0.001 3 |
| 数据的RMS/mm | 20 | 21 |
| 最大滑动量/m | 3.04 | 3.04 |
| 平均滑动量/m | 0.714 | 0.718 |
| 最大滑动量深度/km | 4.50 | 4.47 |
| 计算时间/s | 227 | 1.5×105 |
本文提出了基于方差分量估计的同震滑动分布反演方法，该方法使用方差分量估计方法确定平滑因子和各类数据的权重，突破了方差分量估计方法仅用于各类数据定权的实际应用范围，是一种确定平滑因子的新方法。
模拟算例和实际震例反演结果都证实了本文提出的方法是合理且有效的。从解的概率后验密度分布分析来看，VCE方法得到的结果是F-J方法反演结果的一个解;在考虑计算的时效性的情况下，VCE方法具有计算简单、计算量小和计算效率高的优势，在同震滑动分布反演问题中具有很好的实用价值。
| [1] | Xu Caijun. Progress of Joint Inversion on Geodesy and Geophysics[J]. Geomatics and Information Science of Wuhan University,2001,26(6):555-561 (许才军. 大地测量联合反演理论和方法研究进展[J]. 武汉大学学报·信息科学版,2001, 26(6):555-561) |
| [2] | Xu Caijun, Shen Wenbin, Chao Dingbo. Geophyisical Geodesy Principles and Methods[M]. Wuhan:Wuhan University Press,2006 (许才军,申文斌,晁定波.地球物理大地测量学原理与方法[M]. 武汉:武汉大学出版社,2006 |
| [3] | Xu Caijun, Chen Ting, Zhang Liqin, et al. Joint Inversion Theory of Geophysics and Geodesy and Its Application[M].Wuhan:Wuhan University Press,2015 (许才军,陈庭,张丽琴,等.大地测量地球物理联合反演理论及应用[M].武汉:武汉大学出版社,2015) |
| [4] | Liu Yang.InSAR Inversion Considering Model Error for Hypocenter Parameter[D]. Wuhan:Wuhan University Press,2012 (刘洋. 顾及模型误差的震源参数INSAR反演[[D]. 武汉:武汉大学, 2012) |
| [5] | Zhang Chaoyu,Xu Caijun. Sequential Algorithm of Geodesy Joint Inversion with Automatch Weight Ratio and Its Application[J]. Geomatic and Information Science of Wuhan University,2012,37(10):1 140-1 144 (张朝玉,许才军. 具有自适应权比的大地测量联合反演序贯算法及其应用[J]. 武汉大学学报·信息科学版, 2012,37(10):1 140-1 144) |
| [6] | Fukuda J, Johnson K M. A fully Bayesian Inversion for Spatial Distribution of Fault Slip with Objective Smoothing[J]. Bulletin of the Seismological Society of America, 2008, 98(3):1 128-1 146 |
| [7] | Fukuda J, Johnson K M. Mixed Linearnonlinear Inversion of Crustal Deformation Data:Bayesian Inference of Model, Weighting and Regularization Parameters[J]. Geophysical Journal International, 2010, 181(3):1 441-1 458 |
| [8] | Wen Yangmao. Coseismic and Postseismic Deformation Using Synthetic Aperture Radar Interferometry[D]. Wuhan:Wuhan University,2009(温扬茂.利用INSAR资料研究若干强震的同震和震后形变[D].武汉:武汉大学, 2009) |
| [9] | Funning G J, Parsons B, Wright T J, et al. Surface Displacements and Source Parameters of the 2003 Bam (Iran) Earthquake from Envisat advanced Synthetic Aperture Radar Imagery[J]. Journal of Geophysical Research, 2005, 110(B9):406-416 |
| [10] | Jónsson S, Zebker H, Segall P, et al. Fault Slip Distribution of the 1999 Mw 7.1 Hector Mine, California, Earthquake, Estimated from Satellite Radar and GPS Measurements[J]. Bull Seismol Soc Am, 2002, 92(4):1 377-1 389 |
| [11] | Koch K R, Kusche J. Regularization of Geopotential Determination from Satellite Data by Variance Components[J]. Journal of Geodesy, 2002, 76(5):259-268 |
| [12] | Cui Xizhang, Yu Zongchou, Tao Benzao, et al. Generalized Surveying Adjustment (New Edition)[M]. Wuhan:Wuhan University Press,2009(崔希璋,於宗俦,陶本藻,等. 广义测量平差(新版)[M]. 武汉:武汉大学出版社, 2009) |
| [13] | Okada Y. Surface Deformation Due to Shear and Tensile Faults in a Half Space[J]. Bulletin of the Seismological Society of America, 1985, 75(4):1 135-1 154 |
| [14] | Wei Laisheng. Bayesian Analysis[M]. Hefei:University of Science and Technology of China Press,2013 (韦来生.贝叶斯分析[M] 合肥:中国科学技术大学出版社, 2013) |
| [15] | Graves R W, Wald D J. Resolution Analysis of Finite Fault Source Inversion Using Oneand Three Dimensional Green's Functions 1. Strong Motions[J]. Journal of Geophysical Research, 2001, 6(B5):8 745-8 766 |
| [16] | Rosen P A, Hensley S, Peltzer G M. Updated Repeat Orbit Interferometry Package Released[J]. Eos Trans AGU, 2004,85(5):35-45 |
| [17] | Farr T, Kobrick M. 2000 Shuttle Radar Topography Mission Produces a Wealth of Data[J]. Eos Trans AGU, 2004,85:583-585 |