文章信息
- 魏子卿
- WEI Ziqing
- 完全正常化缔合勒让德函数及其导数与积分的递推关系
- Recurrence Relations for Fully Normalized Associated Legendre Functions and Their Derivatives and Integrals
- 武汉大学学报·信息科学版, 2016, 41(1): 27-36
- Geomatics and Information Science of Wuhan University, 2016, 41(1): 27-36
- http://dx.doi.org/10.13203/j.whugis20150734
-
文章历史
- 收稿日期: 2014-12-09

在地球重力场问题中,常用地球扰动位(地球实际引力位减去正常引力位)模型计算重力场元(大地水准面起伏、垂线偏差、重力异常等)。地球扰动位用球谐级数表示。缔合勒让德函数是球谐级数的组成部分。为数学表示和数值计算的方便,在实践中常规缔合勒让德函数通过乘上一 个随阶n和次m而变的因子加以正常化。常见的因子有n!2m/(n+m)![1, 2]、(-1)mn!/(n+m)![2]、((2n+1)(n-m)!/4π(n+m)!)1/2[3]、((2n+1)(n-m)!δm/(n+m)!)1/2[1, 4, 5](若m=0,δm=1;若m≠0,δm=2)。不同因子导致不同的正常化缔合勒让德函数。上述最后一个因子形成的缔合勒让德函数,通常被特别叫做完全正常化的缔合勒让德函数,也是当今常用的地球引力位模型所用的正常化缔合勒让德函数。
在用地球扰动位模型计算重力场元时,采用完全正常化缔合勒让德函数的递推计算显然更方便。对于重力梯度问题,还需要计算它的导数,对于格网面积平均问题,还涉及到计算它的积分,导数和积分也存在递推问题。考虑到当前流行的地球引力位模型均用完全正常化的缔合勒让德函数,研究完全正常化缔合勒让德函数及其导数和积分的递推关系就具有特别重要的意义。这方面的研究一向为学者们所关注[1, 2, 5]。文献[1, 2]认为完全正常化缔合勒让德函数的递推计算存在数值稳定性问题,它们更倾向于上述第一个正常化因子形成的缔合勒让德函数,因而重点研究了这种所谓新的正常化勒让德函数及其导数和积分的递推问题。文献[5]是研究缔合勒让德函数的积分递推关系的代表作之一,它推导了常规的以及完全正常化的缔合勒让德函数积分的递推公式,不过仅限于单个函数的积分,而未涉及两个函数乘积的积分。本文推导了完全正常化缔合勒让德函数及其导数、积分的递推关系,不只包括单个函数的积分,还包括函数乘积的积分的递推关系,此外还推导了这些函数及其导数、积分的检核式。
1 完全正常化缔合勒让德函数及其导数的递推关系 1.1 完全正常化缔合勒让德函数的递推关系勒让德函数定义为[4]:

式中,

θ代表极距。缔合勒让德函数定义为[4]:
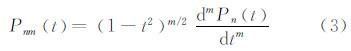
完全正常化缔合勒让德函数与常规缔合勒让德函数的关系被规定为[1, 4, 5, 6, 7]:
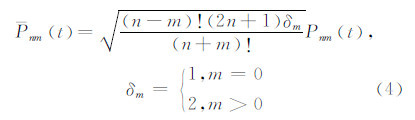
按照式(4),可得到完全正常化缔合勒让德函数的递推关系[1]:
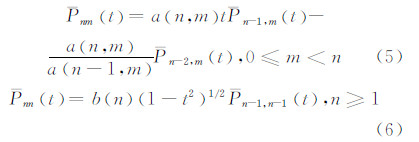
式中,
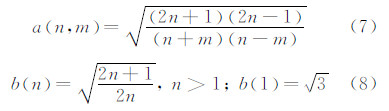
递推起始值:

已知缔合勒让德函数对θ的导数是:
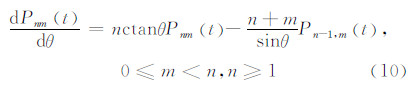
根据式(4)的关系,得到完全正常化缔合勒让德函数对θ的导数:
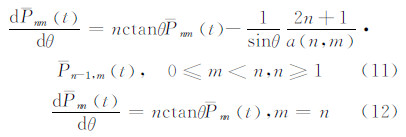
完全正常化缔合勒让德函数对θ的导数的递推关系,可以通过式(5)和式(6)对θ求导得到:
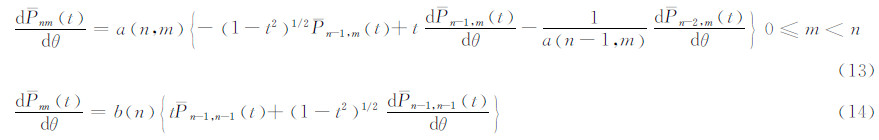
递推起始值:
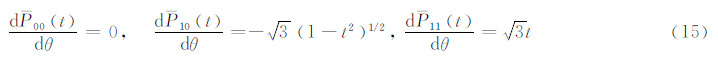
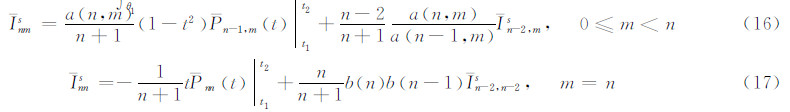
式中,t1=cosθ1,t2=cosθ2。
递推起始值:
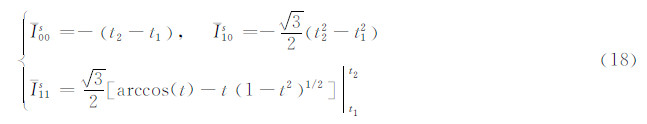
式(5)两端乘sinθ,并对θ积分:
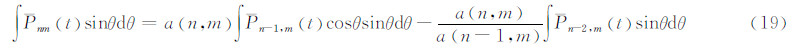
求右端第一项内的不定积分:
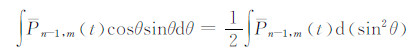
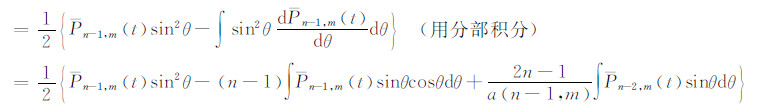
这里用到了式(11)。由此式得:
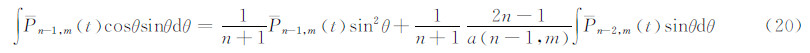
将式(20)代入式(19),并在θ1和θ2之间取定积分,即得式(16)。该式由文献[5]给出。
2.1.2 式(17)的推导 
由此得:
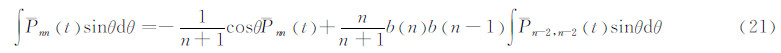
此式在θ1和θ2之间取定积分,即是式(17)。
2.2 积分Inmc(θ1,θ2)=∫θ1θ2Pnm(cosθ)cosθdθ的递推关系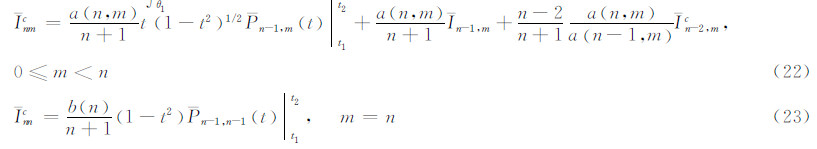
递推起始值:
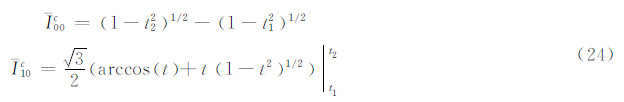
式(5)两端乘cosθ,并对θ积分:
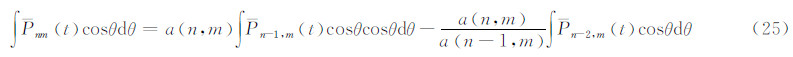
求右端第一项中的不定积分:

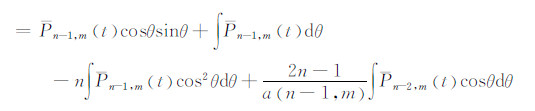
由此式得:
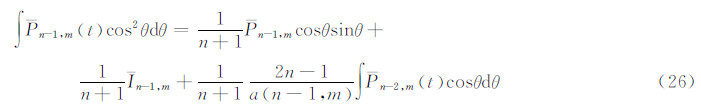
将式(26)代入式(25),并在θ1和θ2之间取定积分,即得式(22)。
2.2.2 式(23)的推导式(6)两端乘cosθ,并对θ积分:
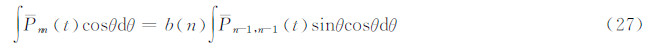
求右端积分项:
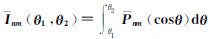
由此式得:
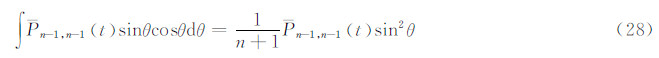
将式(28)代入式(27),并在θ1和θ2之间取定积分,即是式(23)。
2.3 积分Inm(θ1,θ2)=∫θ1θ2Pnm(cosθ)dθ的递推关系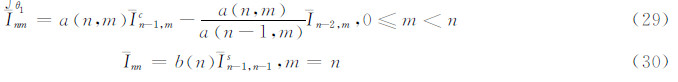
递推起始值:
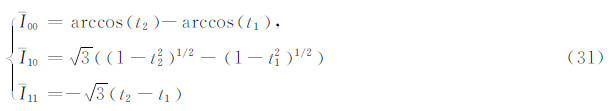
式(29)和式(30)可由式(5)和式(6)两端取定积分得到。
3 完全正常化缔合勒让德函数乘积的积分的递推关系 3.1 积分Inms(θ1,θ2)=∫θ1θ2Pnm(cosθ)Ppq(cosθ)sinθdθ的递推关系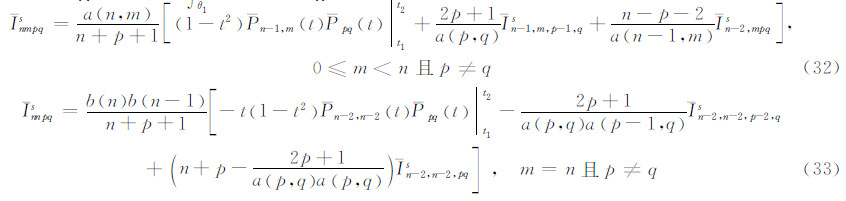
或者

递推起始值:
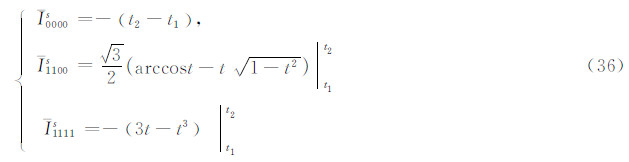
根据式(16),可写出:
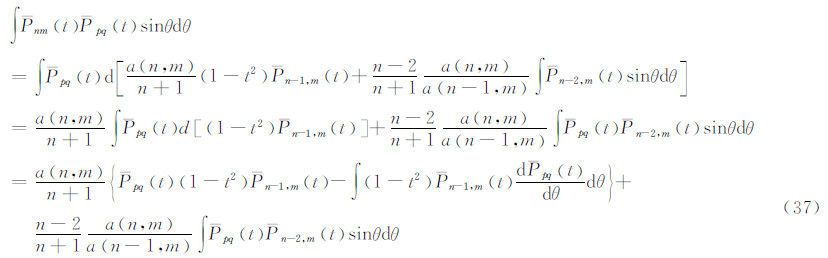
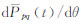 ,然后再将
,然后再将
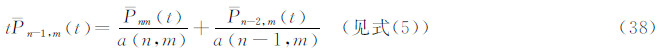
代替所得式中的 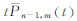 ,整理后即得:
,整理后即得:

由此
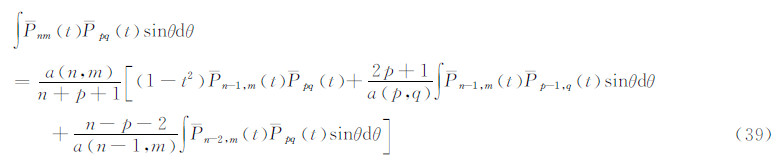
此式在θ1和θ2之间取定积分,即是式(32)。该式参见文献[1]。
3.1.2 式(33)的推导根据式(17),可写出:
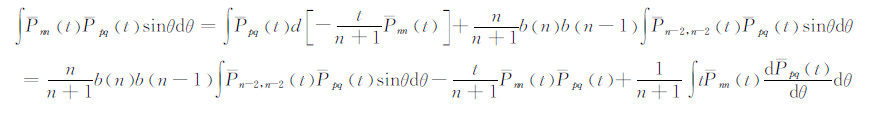
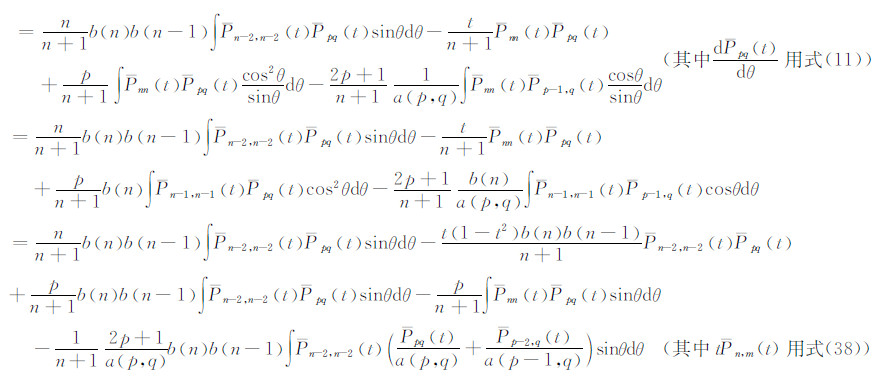
由此式得:
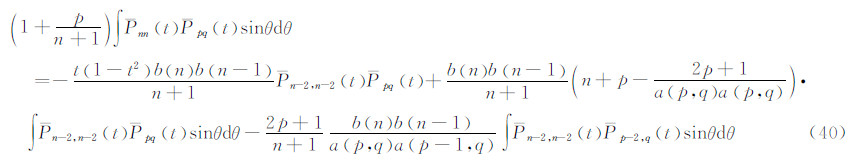
于是得:
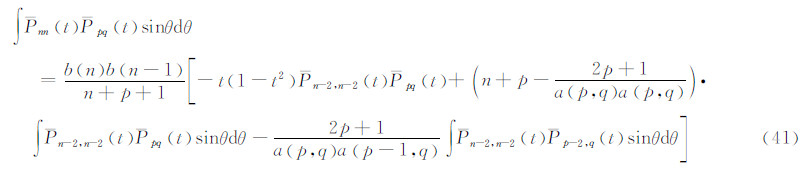
此式在θ1和θ2之间取定积分,即为式(33)。
特别地,当p=q时,a(p,q)=∞,式(41)变为:

此式在θ1和θ2之间取定积分,即为式(35)。
式(34)可由式(32)用符号互换p↔n和q↔m,并令m=n得到。
3.2 积分Inmc(θ1,θ2)=∫θ1θ2Pnm(cosθ)Ppq(cosθ)cosθdθ的递推关系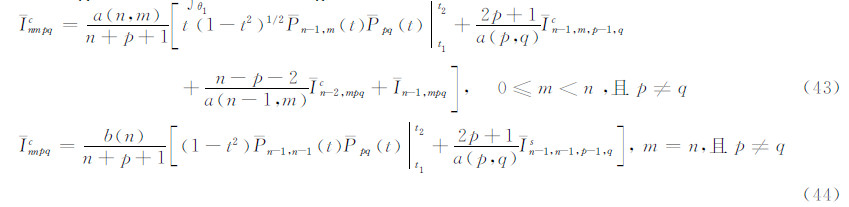
或者
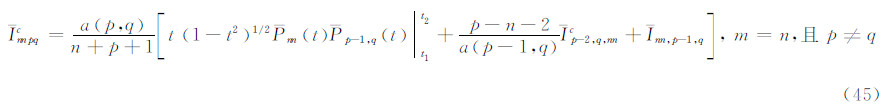
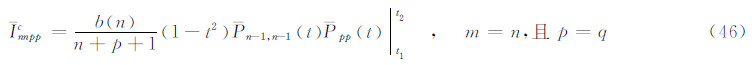
递推起始值:
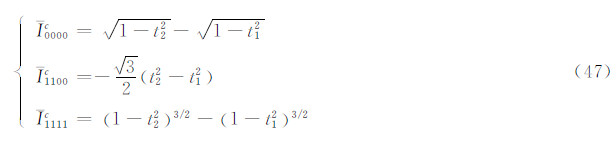
根据式(22),可写出:
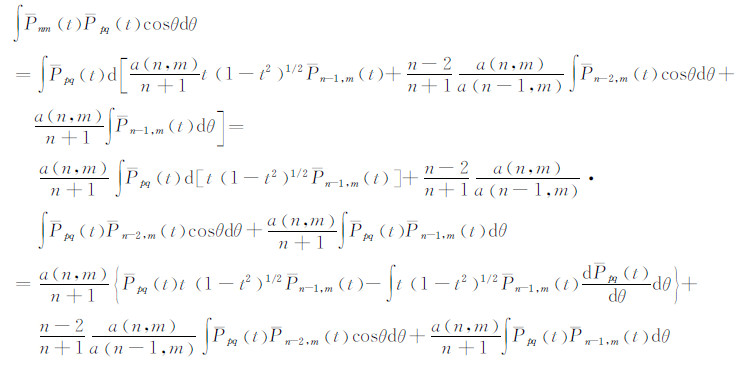
利用式(11)和式(38),得:

此式在θ1和θ2之间取定积分,即为式(43)。
3.2.2 式(44)的推导根据式(23),可写出:
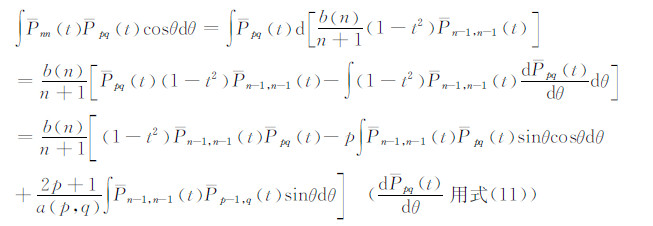
上式右端第二项利用式(6)进行变换,稍经整理,得到:

由此式得:

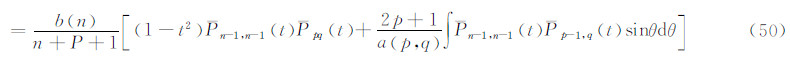
特别地,当p=q时,a(p,q)=∞,(49)式成为:
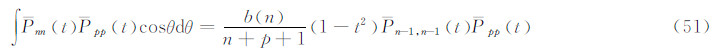
式(50)和式(51)在θ1和θ2之间取定积分,即为式(44)和式(46)。
式(45)可由式(43)用符号互换p↔n和q↔m,并令m=n得到。
3.3 积分Inmpq(θ1,θ2)=∫θ1θ2Pnm(cosθ)Ppq(cosθ)dθ的递推关系
递推起始值:
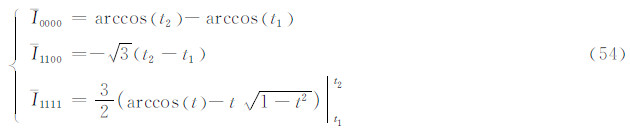
式(52)和式(53)是式(29)和式(30)两端取定积分的结果。
4 完全正常化缔合勒让德函数及其导数和积分的检核式下面给出若干检核式,它们对于检核计算完全正常化缔合勒让德函数及其导数和积分的精度是有用的。
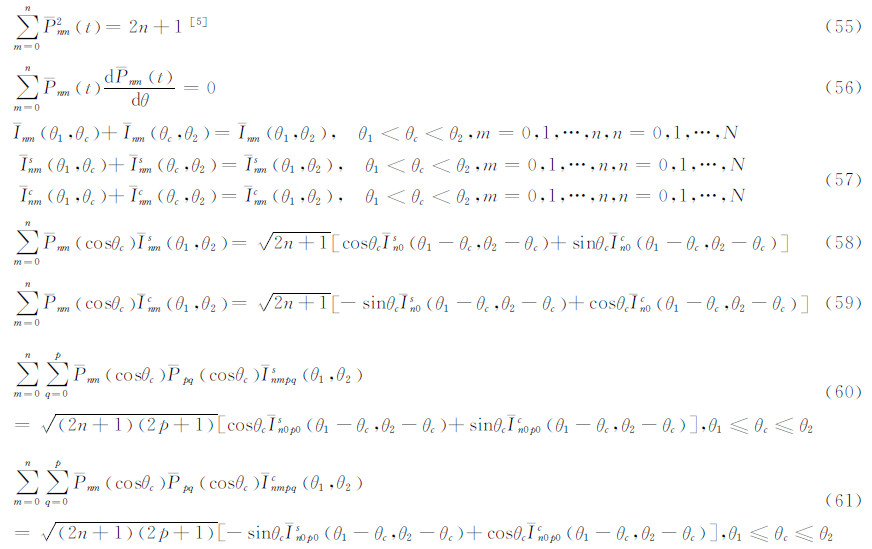
检核式仅整体性地对属于同一n阶的所有m次的量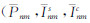 等)进行检核,并不能检查出某一个特别m次的量的具体行为表现。
等)进行检核,并不能检查出某一个特别m次的量的具体行为表现。
下面对以上诸式给予简单证明。式(55)可由球函数的分解定理证明。对式(55)的微分,即得到式(56)。定积分的基本性质使式(57)成立。
4.1 式(58)的推导根据球函数的分解定理,对于n阶m次的完全正常化缔合勒让德函数,可写出:
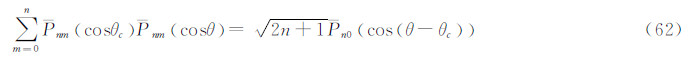
上式两端乘dcosθ,并在θ1和θ2之间取定积分:
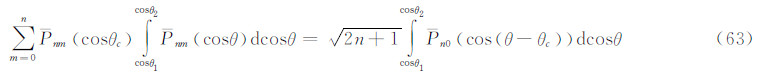
注意到
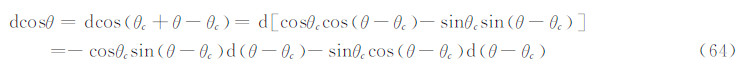
则式(63)给出:
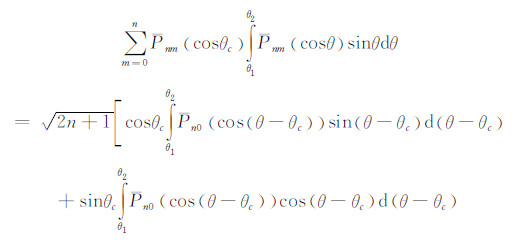
此式即是式(58)。
式(62)两端乘dsinθ,经过类似推导,可得式(59)。
4.2 式(60)的推导对于p阶q次缔合勒让德函数,仿照式(62),写出分解式:
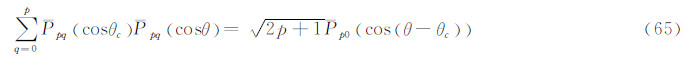
式(62)与式(65)两端相乘得:
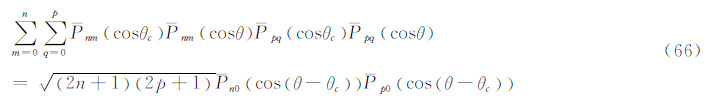
上式两端乘dcosθ,并在θ1和θ2之间取定积分:
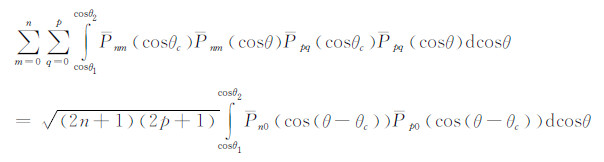
将式(64)代替上式右端的dcosθ,得:
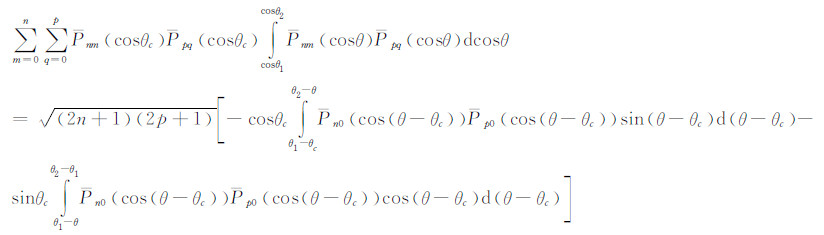
此式即是式(60)。
式(60)两端乘dsinθ,经与上面类似的推导,即得式(61)。
5 结 语本文研究了有关完全正常化勒让德函数的递推关系,导出了若干新的递推关系。同时给出并证明了7种检核式,可用于检核计算的完全正常化缔和勒让德函数及导数和积分的正确性和精度估计。本文推导的递推关系式的正确性已经验证,至于它们的数值稳定性,特别是当其高阶递推时的数值稳定性,尚待进一步研究。
| [1] | Belikov M V. Spherical Harmonic Analysis and Synthesis with the Use of Column-Wise Recurrence Relations[J]. Manuscripta Geodaetica, 1991,16:384-410 |
| [2] | Belikov M V, K A Taybatorov. An Efficient Algorithm for Computing the Earth's Gravitational Potential and Its Derivatives at Satellite Altitudes[J]. Manuscripta Geodaetica, 1992,17:104-116 |
| [3] | Varshalovich D A, Moskalev A N, Khersonskii V K. Quantun Theory of Angular Momentum[M]. Singapore:World Scientific Publ., 1989 |
| [4] | Heiskanen W, Moritz H. Physical Geodesy[M]. San Francisco:W.H. Freeman and Co., 1967 |
| [5] | Paul M K. Recurrence Relations for Integrals of Associated Legendre Functions[J]. Bulletin Geodesique, 1978, 52(3):177-190 |
| [6] | Wang Jianqiang,Li Jiancheng,Zhao Guoqiang,et al. Geoid Undulation Computed Based on Clenshaw Summation[J]. Geomatics and Information Science of Wuhan University, 2010, 35(3):286-289(王建强,李建成,赵国强,等. 利用Clenshaw求和计算大地水准面差距[J]. 武汉大学学报·信息科学版, 2010, 35 (3):286-289) |
| [7] | Tian Jin, Bao Jingyang, Liu Yanchun. Clenshaw Summation in Constructing High Resolution Gravity Field from the Geopotential Coefficient Expression Model[J]. Geomatics and Information Science of Wuhan University, 2005, 30(10):905-908(田晋,暴景阳,刘雁春. 全球位系数模型构建高精度局部重力场的Clenshaw求和[J]. 武汉大学学报·信息科学版, 2005, 30 (10):905-908) |
 2016, Vol. 41
2016, Vol. 41


