文章信息
- 李建成, 徐新禹, 赵永奇, 万晓云
- LI Jiancheng, XU Xinyu, ZHAO Yongqi, WAN Xiaoyun
- 由GOCE引力梯度张量不变量确定卫星重力模型的半解析法
- Approach for Determining Satellite Gravity Model from GOCE Gravitational Gradient Tensor Invariant Observations
- 武汉大学学报·信息科学版, 2016, 41(1): 21-26
- Geomatics and Information Science of Wuhan University, 2016, 41(1): 21-26
- http://dx.doi.org/10.13203/j.whugis20150554
-
文章历史
- 收稿日期: 2015-09-12

2. 武汉大学地球空间环境与大地测量教育部重点实验室, 湖北 武汉, 430079;
3. 钱学森空间技术实验室, 北京, 100094
2. Key Laboratory of Geospace Environment and Geodesy Ministry of Education, Wuhan University, Wuhan 430079, China;
3. Qian Xuesen Laboratory of Space Technology, Beijing 100094, China
重力场与稳态海洋环流探测器(gravity field and steady-state ocean circulation explorer,GOCE)卫星发射于2009年3月,是第一个采用卫星重力梯度测量技术的卫星重力测量任务,250 km的轨道高度和高精度的重力梯度测量使之对重力场的高频信号更为敏感,其科学目标是恢复高分辨率、高精度的全球重力场模型,在100 km空间分辨率上大地水准面精度达到1~2 cm[1]。
目前,利用GOCE卫星实测重力梯度数据反演重力场的方法主要有三种:直接法(direct approach,DIR)、时域法(time-wise approach,TIM)和空域法(space-wise approach,SPW)。欧洲航天局(European Space Agency ,ESA)官方发布的GOCE卫星重力场模型就是采用这三种方法[2],DIR和TIM解是目前国际上获得大家认可的最优卫星重力场模型。除此之外,还有半解析法[3]、张量不变量方法[4, 5]和短弧法[6]。当前,利用引力梯度张量不变量观测值确定重力场的解算方法主要有最小二乘法[7]和积分方法[4],前者理论上更为严密,且可以给出估计模型系数的验后方差,但需要大量的运算,一般需要在高性能计算机上完成;后者虽然效率较高,但需要进行数据归算、格网化以及坐标系的转换等预处理,且不能直接给出估计模型系数的验后方差。
本文提出基于一维快速傅立叶变换(1 dimension fast Fourier transform,1D-FFT)的半解析法(semi-analytical approach,SA)由GOCE引力梯度张量观测值快速解算重力场模型的思路,阐述了张量不变量反演重力场的基本原理,推导了由张量不变量基于半解析法确定全球卫星重力模型的理论公式,并利用模拟数据对该方法的有效性进行了验证。
1 半解析法用于引力梯度张量不变量求解重力场的基本原理某个坐标系下的引力梯度张量的三类不变量 (I1,I2,I3)可表示为[7, 8]:

其中,Vij(i,j=1,2,3)表示引力梯度张量分量,(1,2,3)表示坐标轴的三个方向,选择一个参考模型,可将第二类和第三类张量不变量线性化,得到残余张量不变量:
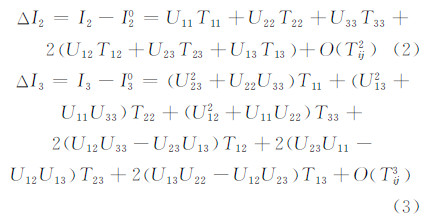
其中,Uij(i,j=1,2,3)表示参考引力梯度张量分量;Tij(i,j=1,2,3)表示残余引力梯度张量分量;I20表示参考模型对应的第二类张量不变量值;I30表示参考模型对应的第三类张量不变量值;O(Tij2)和O(Tij3)分别表示第二类和第三类张量不变量线性化误差。
因为式(2)和式(3)张量不变量与坐标系的选择无关,以上方程同样适用于局部轨道坐标系,(1,2,3)分别对应轨道坐标系的三轴(x,y,z)。引入球近似[4],令参考引力位  (GM为万有引力常数与地球质量的乘积,r为卫星的向径),则有:
(GM为万有引力常数与地球质量的乘积,r为卫星的向径),则有:
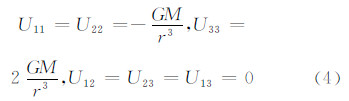
需要说明的是,虽然在球近似过程中Uij取了中心引力位,但在计算式(2)和式(3)中残余引力梯度张量Tij时参考引力位可以自由选取。将式(4)代入式(2)和式(3),同时利用引力位满足Laplace方程的特性,可进一步简化为[4]:
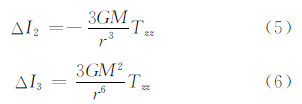

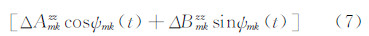
根据式(5)~(7),残余引力梯度张量分量可表示为:
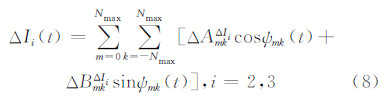
其中,

其中,n、m表示球谐展开的阶和次;nmin=max(k,m)+Δ,如果k和max(k,m)奇偶性相同,Δ=0,否则Δ=1;[2]表示n的变化步长为2;重力场球谐展开的阶数n截断至 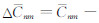
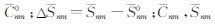 和
和  分别表示正规化的观测值引力位球谐展开系数和参考观测值对应的位系数;
分别表示正规化的观测值引力位球谐展开系数和参考观测值对应的位系数; 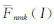 为倾角函数;λnΔIi为残余引力梯度张量不变量对应的特征算子。
为倾角函数;λnΔIi为残余引力梯度张量不变量对应的特征算子。
如果卫星轨道满足圆形、重复、常数倾角的特性,则式(8)就是一个二维傅立叶级数,则重力场求解可分为两步:第一步,首先利用FFT技术计算观测值对应的集总系数ΔAmkΔIi、ΔBmkΔIi,本文采用 1D-FFT算法,直接对沿轨道的观测值进行傅立叶变换,然后将一维FFT系数根据谱映射对应关系得到集总系数[9];第二步将集总系数作为伪观测值,利用它与位系数之间的线性关系来求解[9, 11]。根据式(10),如果将位系数根据次来排列,则可以得到一个严格的块对角的法方程[12],因此可以大大减少运算量。另外,在考虑观测值误差时间序列的相关性时,因为SA方法将观测值转换到频域内,非常容易将先验误差的功率谱密度与频域内观测值的误差对应起来,且观测值误差的方差-协方差矩阵是对角阵,因此处理起来非常容易。
SA方法是目前最快的求解位系数的方法之一,但实际观测值(例如非严格圆形近似重复轨道)往往不能满足采用1D-FFT方法的严格要求,实际计算时可采用迭代方法减弱模型近似的影响,因为式(5)和式(6)的导出中采用了球近似,也需要选择迭代方法来减弱其影响。因此,本文迭代的基本思路是:首先选择一个参考模型,计算残余引力梯度张量不变量观测值,然后计算模型改正值,并将改正值加到参考模型上得到新的模型,再将其作为参考模型重复上面的步骤,直到模型改正值小于某个阈值。此外,因引力梯度张量不变量的计算不依赖于坐标系,因此可以避免坐标系转换带来的影响。
2 数值模拟分析 2.1 数据模拟本文分别采用了两类轨道来模拟引力梯度张量观测值,一是模拟的圆形严格重复轨道,轨道重复比为979/61,倾角选择89.5°,高度为260 km,数据采样为1 s,这样的轨道完全符合SA方法的理论要求;第二类选择GOCE实测简化动力学轨道(precise reduced-dynamic orbits,PRD),从2009-11-01~2009-12-31为一个重复周期的轨道,同样是61 d,将10 s采样的轨道基于拉格朗日多项式内插成1 s采样。模拟观测值选择的模型为EGM2008[13],最高阶次为200,观测值的坐标系选择梯度仪坐标系GRF和LORF,在模拟GRF坐标系下观测值时需要用到梯度仪的惯性姿态数据及地固系与惯性系间的旋转矩阵,本文将EGM2008模型作为“真实模型”。
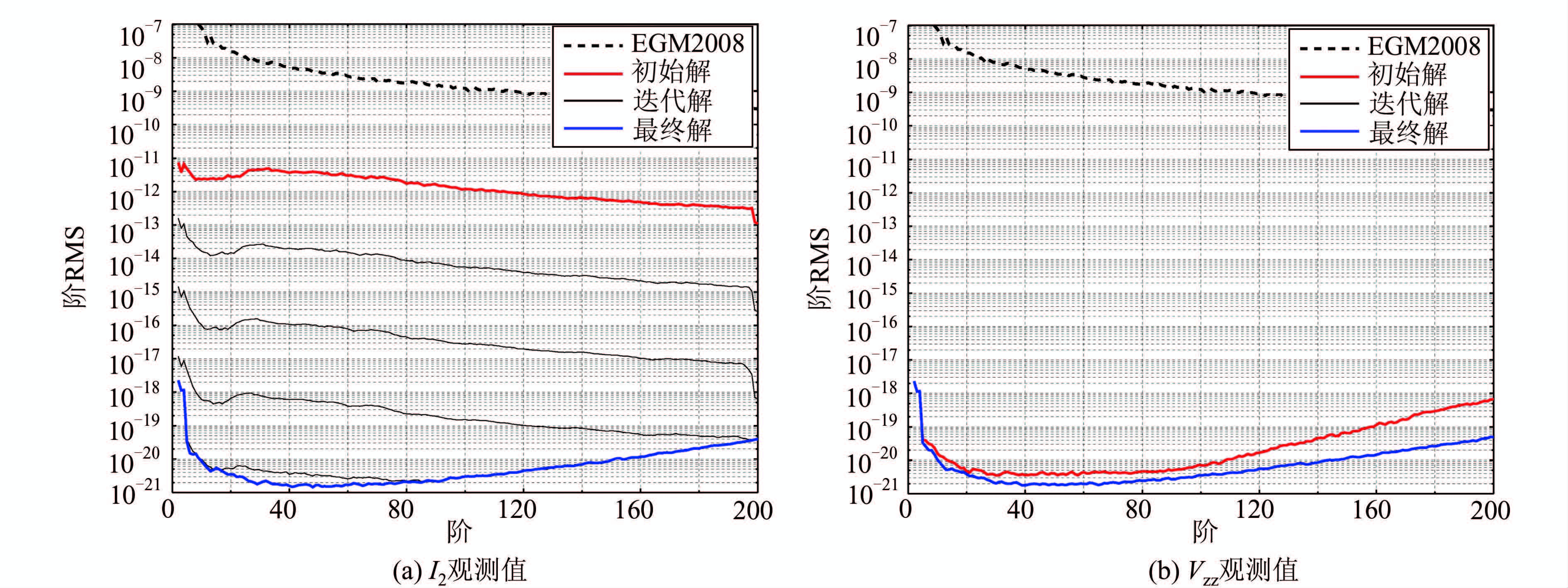
2.2 圆形严格重复轨道的模拟观测值为了验证本文所提出方法的正确性,同时验证采用迭代过程减弱球近似误差影响的可行性,采用LORF坐标下I2观测值,基于SA方法求解了200阶次模型,初始参考模型选择EGM96,求解模型的迭代解与真实模型差异的阶均方根(root mean square,RMS),计算公式可参考文献[14],如图 1(a)所示。为了比较,同时给出了采用Vzz观测值由SA方法求解的结果,如图 1(b)所示,Vzz观测值解算的原理和具体过程可参考文献[11]。从图 1中可以看出,对于圆形严格重复轨道,采用观测值Vzz由SA方 法求解时不需要迭代,此时观测值的特点严格满足SA方法的理论模型要求,求解模型的差异仅来自于计算机的计算误差;采用I2观测值也可获得非常高精度的结果,但需要经过4次和5次迭代才可以逐渐收敛到真实值,说明采用迭代方法可以减弱球近似引起误差。从图 1中的结果可以看出,在无误差的情况下,两种观测值可以获得几乎一致的结果,验证了将SA方法运用于张量不变量观测值解算的思想。
|
| 图 1 由I2和Vzz观测值基于SA方法求解模型误差的阶RMS Fig. 1 Degree RMS of Error of the Solutions Based on the SA Approach from the I2 and Vzz Observations |
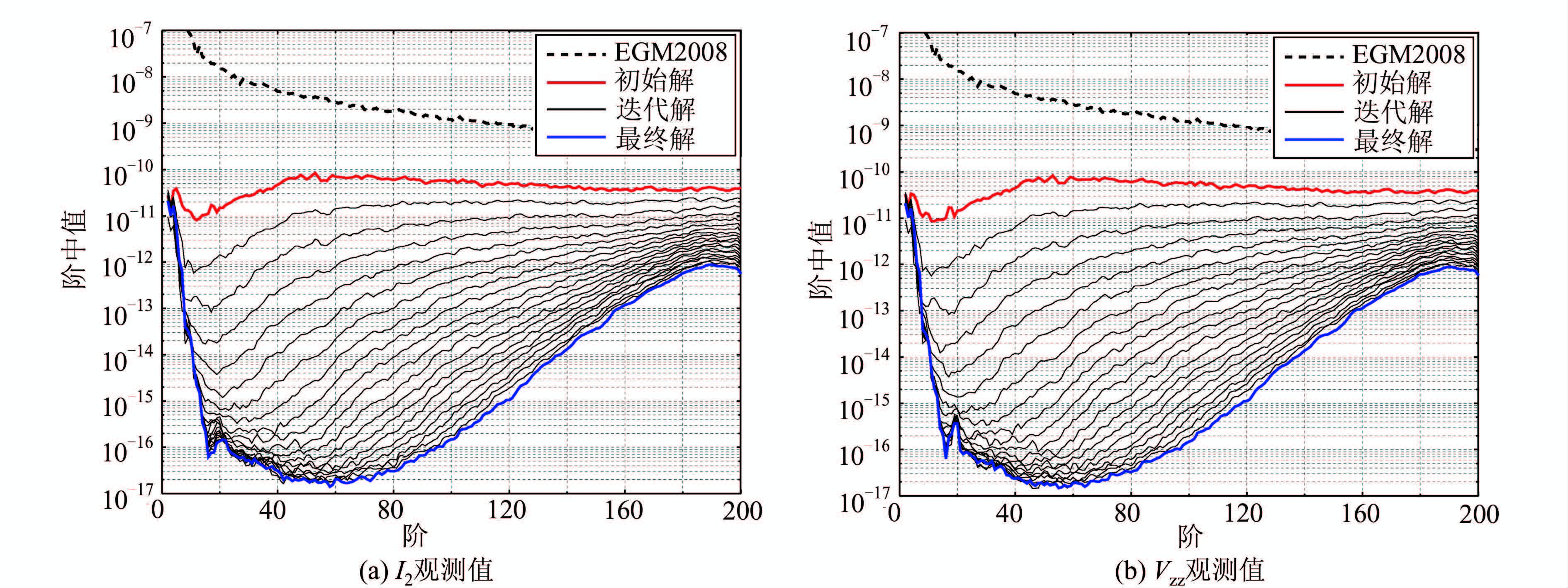
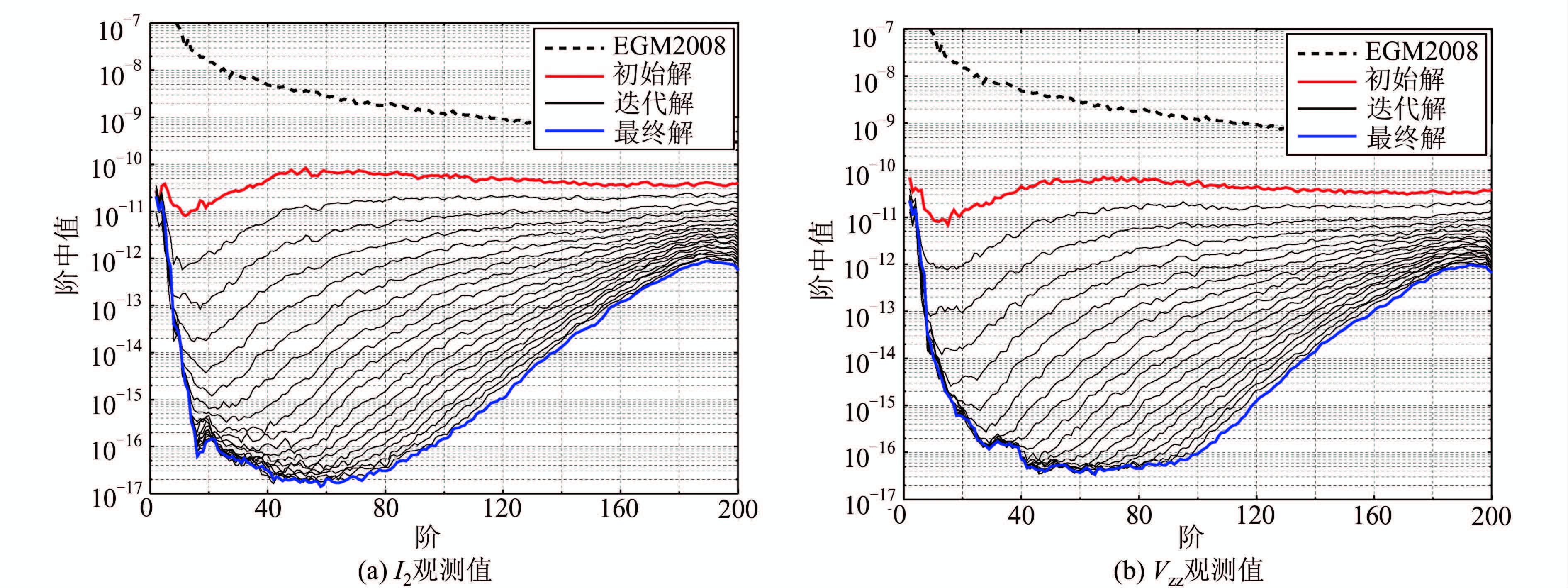
为了进一步分析基于I2观测值求解GOCE重力场模型的能力,下文基于GOCE的实测轨道进行分析。首先讨论无噪声的观测值,分别利用61 d GOCE实测轨道上GRF和LORF下的模拟观测值Vzz和第二类张量不变量I2求解全球重力场模型,模型误差的阶中值如图 2和图 3所示。考虑到GOCE轨道96.7°的轨道倾角使观测值在两极有半径为6.7°的空白区,这会导致重力场模型低次系数的误差较大,因此,本文采用了阶中值来描述[15]。从图 2和图 3中可以看出,GRF和LORF下的Vzz和I2观测值均能收敛到很好的解,其中因为张量不变量观测值不依赖于坐标系的选择,其在GRF和LORF下求解的结果一样。当观测值在LORF下时,Vzz和I2两类观测值可以获得一致的结果;当使用GRF下的观测值时,采用Vzz观测值求得解的精度略差于I2,这主要是因为SA方法在理论上要求Vzz观测值应该在LORF下,但GOCE任务LORF和GRF坐标系的指向并不相同,其偏差可达±3.5°[16]。利用EGM2008模型模拟的两个坐标系下Vzz观测值差异的均值为-0.23 E(1 E= 10-9/m2),最小值为-2.89 E,最大值为0.01 E,RMS为0.40 E。考虑到GOCE实测观测值Vzz的误差水平为0.020 E[17],因此,两个坐标系之间观测值差异的RMS是实测观测值误差的20倍,直接利用GRF下Vzz观测值求解必然会对求解结果产生影响。但迭代收敛结果表明Vzz分量也获得了很好的结果,这说明迭代过程同样可在一定程度上减弱因坐标系不一致所产生的误差。
|
| 图 2 由LORF下I2观测值和Vzz观测值基于SA方法求解模型误差的阶中值 Fig. 2 Degree Median of Error of the Solutions Based on SA Approach from I2 and Vzz Observations in LORF |
|
| 图 3 由GRF下I2观测值和Vzz观测值基于SA方法求解模型误差的阶中值 Fig. 3 Degree Median of Error of the Solutions Based on SA Approach from I2 and Vzz Observations in GRF |
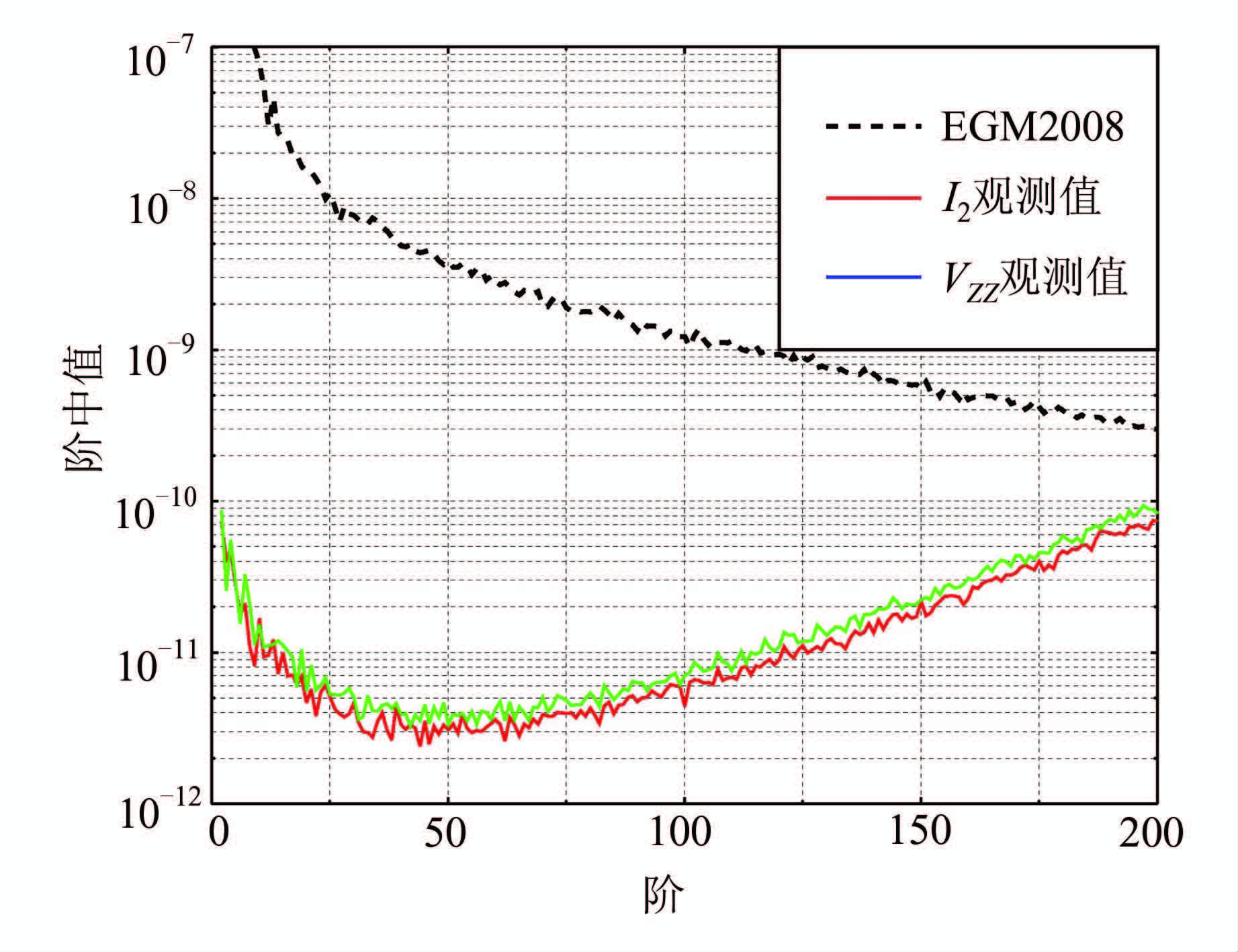
其次,对GRF下模拟梯度张量观测值的所有分量均加入方差为5 mE (1 mE=10-3 E)的白噪声,分别用Vzz和I2观测值求解重力场模型,估计模型与真实模型差异的阶中值如图 4所示。从图 4中可以看出,由I2求解模型误差的阶中值略小于由Vzz求解模型误差的阶中值,同样说明在白噪声模拟的情况下,基于I2观测值求解模型的精度略优于Vzz求解模型,这和采用无误差的观测值得到的结果一致。
|
| 图 4 由GRF坐标系下I2和Vzz 观测值基于SA方法求解模型误差的阶中值 Fig. 4 Degree Median of Error of the Solutions Based on SA Approach from I2 and Vzz Observations in GRF |
本文研究了利用张量不变量观测值求解重力场的理论与方法,提出将半解析法用于该观测量的快速解算,推导了该方法用于张量不变量观测值解算的理论公式,并给出了求解的具体步骤。采用89.5°倾角的圆形严格重复轨道下第二类引力梯度张量不变量观测值I2可以完全恢复重力场模型,验证了本文提出方法的正确性。本文利用GOCE实测轨道上GRF和LORF下引力梯度张量模拟观测值,基于无噪声和包含白噪声的I2观测值基于半解析法确定了全球重力场模型,结果说明通过迭代过程可有效减弱非圆形、近似重复轨道、球近似误差及线性化误差的影响,验证了利用GOCE张量不变量观测值基于半解析法求解全球重力场模型的可行性。同时,求解结果还说明基于I2观测值求解模型的精度略优于Vzz求解模型。
| [1] | ESA. Gravity Field and Steady-State Ocean Circulation Mission[R]. Report for Mission Selection of the Four Candidate Earth Explorer Missions, ESA Publications Division, ESA, Paris, 1999 |
| [2] | Pail R, Bruinsma S, Migliaccio F, et al. First GOCE Gravity Field Models Derived by Three Different Approaches[J]. Journal of Geodesy, 2011, 85(11):819-843 |
| [3] | Mayrhofer R, Pail R, Fecher T. Quicklook Gravity Field Solutions as Part of the GOCE Quality Assessment[C]. The ESA Living Planet Symposium, Bergen, Norway, 2010 |
| [4] | Yu J H, Wan X Y. Recovery of the Gravity Field from GOCE Data by Using the Invariants of Gradient Tensor[J]. Sci China Earth Sci, 2013, 56(7):1 193-1 199 |
| [5] | Cai J, Sneeuw N, Baur O. GOCE Gravity Field Model Derived from the Rotational Invariants of the Gravitational Tensor (Poster)[C]. BMBF Geotechnologien Statusseminar "Erfassung des Systems Erde aus dem Weltraum IV", Stuttgart, Germany, 2011 |
| [6] | Schall J, Eicker A, Kusche J. The ITG-GOCE02 Gravity Field Model from GOCE Orbit and Gradiometer Data Based on the Short Arc Approach[J]. Journal of Geodesy, 2014, 88(4):403-409 |
| [7] | Baur O, Sneeuw N, Grafarend E W. Methodology and Use of Tensor Invariants for Satellite Gravity Gradiometry[J]. Journal of Geodesy, 2008, 82(4/5):279-293 |
| [8] | Yu J H, Zhao D M. The Gravitational Gradient Tensor's Invariants and the Related Boundary Conditions[J]. Sci China Earth Sci, 2010, 53(5):781-790 |
| [9] | Sneeuw N. A Semi-Analytical Approach to Gravity Field Analysis from Satellite Observations[D]. Munich, Germany:Technical University Munich, 2000 |
| [10] | Schrama E J O. The Role of Orbit Errors in Processing of Satellite Altimeter Data[D]. Delft, Netherlands:Delft University of Technology, 1989 |
| [11] | Xu Xinyu, Li Jiancheng, Jiang Weiping, et al. The Fast Analysis of GOCE Gravity Field[C]. International Association of Geodesy Symposia:Observing Our Changing Earth, Perugia, Italy, 2007 |
| [12] | Colombo O L. Numerical Methods for Harmonic Analysis on the Sphere[R]. Dept. of Geodetic Science, The Ohio State University, Columbus, Ohio,1981 |
| [13] | Pavlis N K, Holmes S A, Kenyon S C, et al. The Development and Evaluation of the Earth Gravitational Model 2008 (EGM2008)[J]. Journal of Geophysical Research:Solid Earth, 2012, 117(4):1 978-2 012 |
| [14] | Xu Xinyu, Li Jiancheng, Zou Xiancai, et al. Simulation Study for Recovering GOCE Satellite Gravity Model Based on Space-Wise LS Method, Acta Geodaetica et Cartographica Sinica, 2011, 40(6):697-702(徐新禹, 李建成, 邹贤才, 等. 基于空域最小二乘法求解GOCE卫星重力场的模拟研究, 测绘学报, 2011, 40(6):697-702) |
| [15] | Sneeuw N, van Gelderen M. The Polar Gap[M]//Sansò F, Rummel R. Geodetic Boundary Value Problems in View of the One Centimeter Geoid. New York:Springer, 1997 |
| [16] | EGG-C. GOCE Level 2 Product Data Handbook[EB/OL].https://earth.esa.int/documents/10174/1650485/GOCE_Product_Data_Handbook_Level-2, 2010 |
| [17] | Rummel R, Yi W, Stummer C. GOCE Gravitational Gradiometry[J]. Journal of Geodesy, 2011, 85(11):777-790 |
 2016, Vol. 41
2016, Vol. 41



