文章信息
- 顾留碗, 王春, 李鹏, 王靖, 王壮壮
- GU Liuwan, WANG Chun, LI Peng, WANG Jing, WANG Zhuangzhuang
- 利用DEM提取山顶点精度研究
- Research on Mountain Top Extraction Accuracy Based on DEM
- 武汉大学学报·信息科学版, 2016, 41(1): 131-135
- Geomatics and Information Science of Wuhan University, 2016, 41(1): 131-135
- http://dx.doi.org/10.13203/j.whugis20130386
-
文章历史
- 收稿日期: 2014-02-17

山顶点是指局部区域内海拔高程的极大值点,表现为在各方向上都为凸起[1]。山顶点是对地表形态最具控制性的特征点位之一,对地貌形态、水文过程、植被分布等具有重要的影响[2]。山顶点的准确识别与提取受到国内外一些学者的广泛关注[3, 4]。文献[5]从地形特征点的几何形态特征出发研究了由DEM提取山顶点的算法,但是由于DEM不可避免存在地形描述误差及地形起伏变化的复杂性[6],该算法提取的结果中存在大量伪山顶点。对此,文献[7]设计了基于邻域分析和封闭等高线辅助判别的山顶点识别与提取模型,在一定程度上虽然能够剔除部分伪山顶点,但邻域范围阈值与等高线基准位置的设定存在主观性。总体来讲,现有的基于DEM及地形图的山顶点识别与提取模型主要解决了局部区域内海拔高程极大值点的识别与提取,在丘陵、山地等区域具有较好的实用性,但是在局部起伏比较复杂的地形区域,现有模型缺乏有效的指标和控制手段甄别出实际山顶点。因此,本文根据山顶点的地表形态特征,采用基准面逐次下降方法,设计了顾及地形地貌学含义的山顶点提取模型,较好地解决了伪山顶点的识别与剔除问题,为利用DEM进行地形地貌模式识别的技术理论奠定了基础,同时该研究在宏观尺度上对实现地貌形态特征定量化描述与标识,进一步充实和完善数字地貌学的研究内容和方法有重要意义。
1 山顶点提取模型山顶点是一个容易意会却难以精确量化的地理对象。在地貌学中,山被定义为海拔高度500 m以上、相对起伏大于200 m、坡度又较陡的高地,山自上而下分为山顶、山坡和山麓三部分。山顶地貌形态的数学定义可以理想地利用地形曲面来表达[8]。设地形曲面为T,a和b为T上任意两点,其高程分别为Ha和Hb,θ为Ha和Hb间的高差阈值,ΔH为a、b两点高差;对于T上任意点i,若满足下列条件:

式中,Bi为过点i的平面;Ci为过i点的等高线;T是以b为顶的山坡面;而满足点集M={Ci,i∈[a,b]}的点构成山坡M。
实现上述定义的山顶点的识别与提取,首先要界定山的范围。在形态上,山顶点一定是局部区域范围内的最高点,但是局部区域范围内的最高点不一定是山顶点。如图1所示,A~D都是局部最高点,但是否是山顶点,自然状态下需要依据相邻山顶点的起伏情况确定。假定E点是从局部最高点D到点C的所有紧贴地面的DC连线的最高谷底点,记DE的高差为Hde,则Hde是判定D是否是山顶的主要依据。在实际生活中,D要被被判定为山顶点,则Hde必须具有一定的大小,否则D仅是局部略有凸起的山脊点,不会被判定为山顶点。因此,本文以Hde为基本依据,提出了基于最大起伏度阈值的山顶点提取模型。所谓最大起伏度阈值,指的是最大的Hde,简言之就是当前山顶点与其周围所有更高的山顶点地面连线形成的最高谷底点的高差值。

|
| 图 1 山顶点示意图 Fig. 1 Diagram of Mountain Tops |
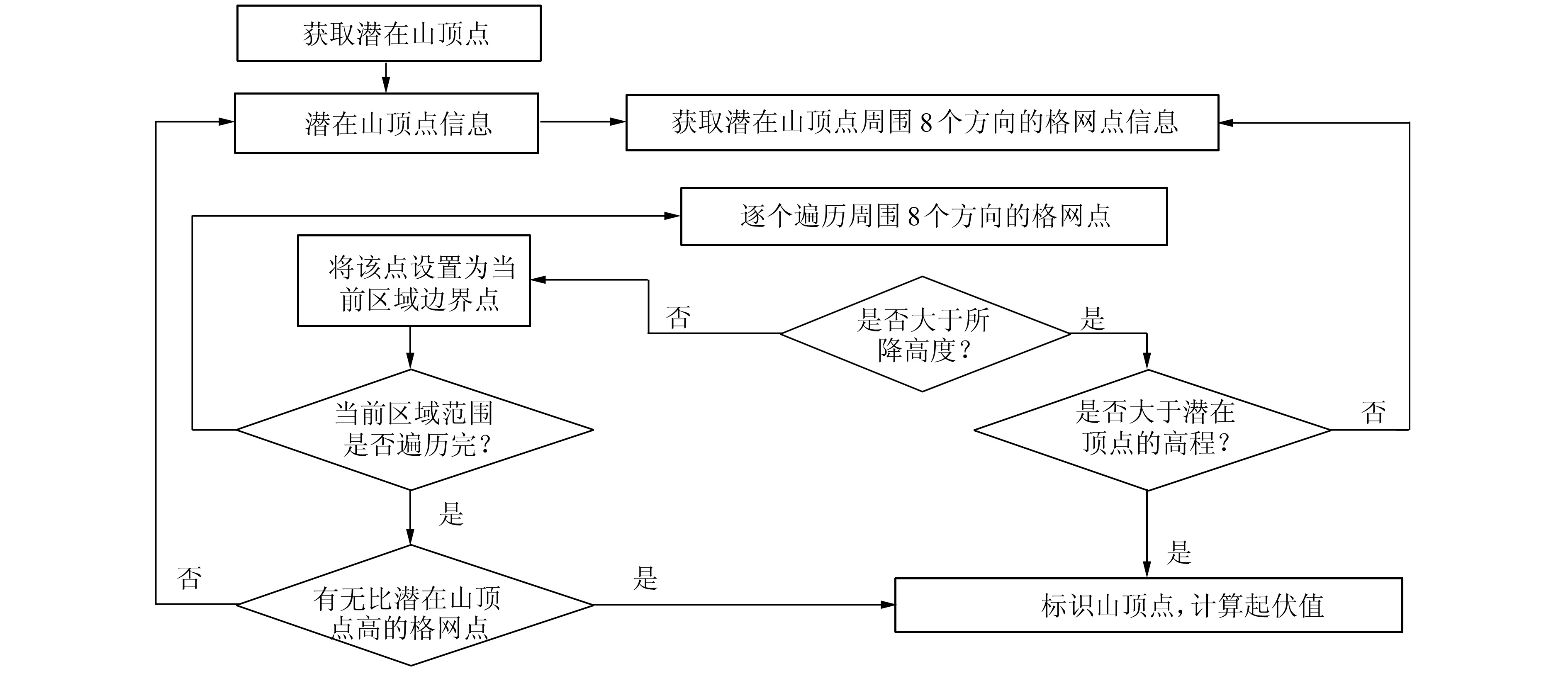
图2为基于最大起伏度阈值的山顶点提取技术流程。具体实现过程为:首先选定待分析的局部最高点作为潜在山顶点;然后以潜在山顶点为起始基准面,按照设定的高差步距下降基准面,标识基准面割地形所得到的包含该潜在山顶点的区域,判断该区域是否存在比潜在山顶点更高的其他地面点,或者基准面割地形所得到的区域已覆盖全部研究区;如果条件为真,停止下降基准面,并记录基准面累计下降的高程值作为该山顶点的最大起伏度阈值;重复上述过程,指导处理完所有潜在山顶点。
|
| 图 2 基于最大起伏度阈值的山顶点提取技术流程 Fig. 2 Process of Extracting Peaks Based on the Threshold of Maximum |
实验样区位于陕西绥德韭园沟黄土丘陵地形区,样区平均坡度28.6°,平均地形起伏度7.49 m。实验数据制作过程为:首先基于1∶5万数字地形图数据,依据国家1∶5万DEM产品生产技术流程,制作出5 m DEM数据,主要用于测试本文山顶点提取模型的正确性;然后在10 m×10 m、25 m×25 m、50 m×50 m、100 m×100 m、500 m×500 m的范围内,分别采用均匀布设基准点的方法,各自生成4幅不同格网点布设位置的10 m、25 m、50 m、100 m和500 m DEM,主要用于分析DEM格网点布设位置及格网分辨率对山顶点提取精度的影响特征。
图3为基于实验样区5 m DEM提取的20 m最大高差阈值的山顶点示意图(局部)。提取结果表明,该模型逻辑严密,能够依据最大起伏度阈值准确识别和提取山顶点,克服了文献[7]及传统提取方法在剔除伪山顶点时的主观性和不确定性。

|
| 图 3 黄土丘陵山顶点提取结果示意图 Fig. 3 Schematic Diagram of Extraction Results for Mountain Tops in Loess Hills |
图4为实验样区4种不同格网点布设位置的10 m、25 m、50 m、100 m和500 m DEM中,本文模型提取的山顶点平面位置及高程变化示意图。图4中,黑圆点及注记为根据参考真值DEM提取的山顶点及其高程,其他4种不同颜色的+点及注记为根据不同格网点布设位置DEM提取的山顶点及其高程。由实验结果得出以下结论。

|
| 图 4 黄土丘陵不同格网点布设位置DEM中山顶点空间位置变化示意图 Fig. 4 Spatial Location Changes of Loess Hill Tops Extracted from DEMs with Different Grid Sizes |
1) 对于已知综合尺度的DEM,存在最优DEM格网分辨率阈值(如本文中的25 m DEM)。
2) 当实际DEM格网分辨率高于或近似等于最优DEM格网分辨率阈值时(如本文中的10 m、25 m DEM),基于DEM提取的山顶点空间位置具有较高精度。其中,山顶点的平面位置误差不会超过d/2(d为DEM格网分辨率大小),高程精度不会低于该DEM标定的高程精度。
3) 当实际DEM格网分辨率低于最优DEM格网分辨率阈值时(如本文中的50 m、100 m和500 m DEM),基于该DEM提取的山顶点数量、平面位置及高程等信息,与原始综合地形中的山顶点存在一定的差异,且DEM格网分辨率越低,这种不确定性差异会越大,基于该DEM已难以准确识别和提取原始综合地形中的山顶点。
表1为基于我国1∶100万DEM(格网大小1km)提取的海拔高度500m以上、相对起伏大于200m的中国内陆(除所有海岛以外的中国领土)山顶点统计信息。分析表1可以得出如下信息。
| 海拔/m | 山顶点 数量 | 不同起伏度阈值区间的山顶点数量 | |||||||
| 200~ 500 m | 500~ 1 000 m | 1 000~ 2 000 m | 2 000~ 3 000 m | 3 000~ 4 000 m | 4 000~ 5 000 m | 5 000~ 6 000 | 6 000 m以上 | ||
| 500~1 000 | 6 698 | 6 486 | 212 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 000~2 000 | 8 688 | 7 885 | 740 | 63 | 0 | 0 | 0 | 0 | 0 |
| 2 000~3 000 | 4 310 | 3 765 | 496 | 48 | 1 | 0 | 0 | 0 | 0 |
| 3 000~4 000 | 4 012 | 3 519 | 434 | 53 | 5 | 1 | 0 | 0 | 0 |
| 4 000~5 000 | 7 663 | 6 988 | 615 | 51 | 7 | 2 | 0 | 0 | 0 |
| 5 000~6 000 | 7 768 | 6 829 | 835 | 97 | 7 | 0 | 0 | 0 | 0 |
| 6 000~7 000 | 863 | 526 | 213 | 117 | 7 | 0 | 0 | 0 | 0 |
| 7 000以上 | 36 | 3 | 9 | 8 | 10 | 4 | 1 | 0 | 1 |
| 合计 | 40 038 | 36 001 | 3 554 | 437 | 37 | 7 | 1 | 0 | 1 |
1) 基于我国1∶100万DEM提取的满足海拔高度500 m以上、相对起伏大于200 m的中国内陆山顶点共有40 038个,其中,海拔高度大于7 000 m和8 000 m的各有36座和4座。这一研究数据和现有一些报道存在一些出入,如一些网上报道我国大于8 000 m的山峰有7座,大于7 000 m的山峰有10座或140座,出现差异的原因一方面可能是DEM数据质量的问题,另一方面主要是判定标准的不同,这些问题有待进一步研究。
2) 由于中国三级阶地总体地形特征的影响,不同海拔的山顶点出现较强规律的三级阶地分布特征,但不同起伏度的山顶点在空间上呈现显著的交错分布特征,而且在数量上以200~500 m起伏度阈值为第一集中区,占89.9%;以500~1 000 m起伏度阈值为第二集中区,占8.9%;大于1 000 m起伏度阈值的山顶点数量较少,仅为483座,占1.2%。
3 结 语本文依据山顶点的地貌学定义及其在DEM中的形态特征,提出了最大起伏度阈值指标,为实现山顶点的精确数学描述提供了理论与方法参考。在此基础上,本文采用基准面下降方法,构建了以最大起伏度阈值为客观限制条件的新型山顶提取模型,能够准确地在DEM中识别和提取各种起伏度阈值的山顶点,具有较好的实用价值。
特征点、特征线、特征面等特征地形,是描述地貌形态及进行地貌类型划分、反演预测地貌发育等自然地理学研究的基础因素,虽然现有的DEM数字地形分析技术已建立了丰富的点状、线状和少量面状特征地形的识别与提取模型,但很多模型仅具有局部适宜性,并不能提取符合地形地貌学定义的特征地形信息,有待进一步深入研究和完善。
本文所用的DEM数据为国家基础地理数据库中格网大小为1 000 m的1∶100万DEM。由于DEM数据精度的影响,所提取的山顶点数量及空间位置可能存在一些偏差。随着现代对地观测技术的发展和基础地理数据共享服务政策的完善,有望基于高分数据完成更为准确的山顶点提取与分析。
| [1] | Tang Guoan, Li Fayuan, Liu Xuejun.Digital elevation model tutorial (Second Edition)[M]. Beijing:Science Press, 2010 (汤国安,李发源,刘学军.数字高程模型教程(第二版)[M].北京:科学出版社,2010) |
| [2] | Tang Guoan, Gong Jianya, Chen Zhengjiang, et al. A Simulation on the Accuracy of DEM Terrain Representation[J]. Acta Geodaetica et Cartographica Sinica,2001,30(4):361-365(汤国安.龚健雅,陈正江,等.数字高程模型地形描述精度量化模拟研究[J].测绘学报,2001,30(4):361-365) |
| [3] | Cang Xuezhi, Tang Guoan, Zhong Teng, et al. Classification of Peaks and Digital Expression of Their Spatial Pattern[J]. Journal of Nanjing Normal University(Natural Science Edition),2010,33(1):136-140(苍学智,汤国安,仲腾,等.山顶点类型及其形态特征数字表达[J].南京师大学报(自然科学版),2010,33(1):136-140) |
| [4] | Luo Mingliang. Research on Terrain Feature Point Cluster based onDEMs[D]. Beijing:Chinese Academy of Sciences, 2008(罗明良.基于DEM的地形特征点簇研究[D].北京:中国科学院,2008) |
| [5] | Wood J. The Geomorphological Characterization of Digital Elevation Models[D]. Lancaster, U K:University of Lancaster, 1996 |
| [6] | Wang Chun, Liu Xuejun, Tang Guoan, et al. Morphologic Fidelity of Grid Digital Elevation Model[J]. Geomatics and Information Science of Wuhan University, 2009, 34(2):46-49(王春, 刘学军, 汤国安,等. 格网DEM地形模拟的形态保真度研究[J]. 武汉大学学报·信息科学版, 2009, 34(2):46-49) |
| [7] | Chen Panpan. A Research on Surface Peaks and its Attribution's Spatial Distributing Based on DEM[D]. Xi'an:Northwest University,2006(陈盼盼. 基于DEM的山顶点及其属性空间分异规律研究[D].西安:西北大学,2006) |
 2016, Vol. 41
2016, Vol. 41



