文章信息
- 曹亚妮, 吴芳华, 王丽君, 李嘉星
- CAO Yani, WU Fanghua, WANG Lijun, LI Jiaxing
- 基于元拓扑关系的线面空间关系集成表达模型
- The Integrated Representation Model of Line-Region Spatial Relations Based on Meta-relations
- 武汉大学学报·信息科学版, 2016, 41(1): 123-130
- Geomatics and Information Science of Wuhan University, 2016, 41(1): 123-130
- http://dx.doi.org/10.13203/j.whugis20130828
-
文章历史
- 收稿日期: 2015-03-03

2. 地理信息工程国家重点实验室, 陕西 西安, 710054;
3. 西安测绘研究所, 陕西 西安, 710054;
4. 信息工程大学地理空间信息学院, 河南 郑州, 450052;
5. 61363部队, 陕西 西安, 710054
2. State Key Laboratory of Geo-information Engineering, Xi'an 710054, China;
3. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
4. Geographic Spatial Information Institute, Information Engineering University, Zhengzhou 450052, China;
5. Unit 61363, Xi'an 710054, China
20世纪80年代,空间关系的研究就得到了国际学术界的高度重视[12]。空间关系的研究在空间冲突检测[3, 4]、制图综合[5, 6, 7]、空间数据建模、空间查询和分析等方面都有着重要的应用。随着应用的不断深入和细化,人们发现现有的四交模型、九交模型,基于Voronoi图的九交模型、四交差模型,以及基于区域连接演算的空间逻辑模型等只适用于简单拓扑关系的描述和判断,而无法满足复杂空间关系细化描述和计算的实际应用需求[4, 5, 6, 7, 8]。因此,对空间关系进行细化、集成描述,以解决生产与工程实践中的问题,已经成为空间关系的一个重要研究方向。近年来,许多学者在这方面进行了研究,取得了一些进展[9, 10, 11, 12, 13]。但是,还存在以下问题:(1)描述的线面空间关系不够直观,不利于空间关系的比较和判断;(2)交分量的分解粒度太小,较为复杂,不利于记忆与使用;(3)依据描述方法或模型,较难复原空间拓扑关系图;(4)对集成描述方法的优劣缺乏评判指标。基于上述分析,本文研究了线面简单拓扑关系及其分类方法,提出了能够组成线面复杂拓扑关系的3类6种元拓扑关系,基于元拓扑关系建立了一种线面空间关系的集成表达模型,并对模型的性能进行了分析与评价。
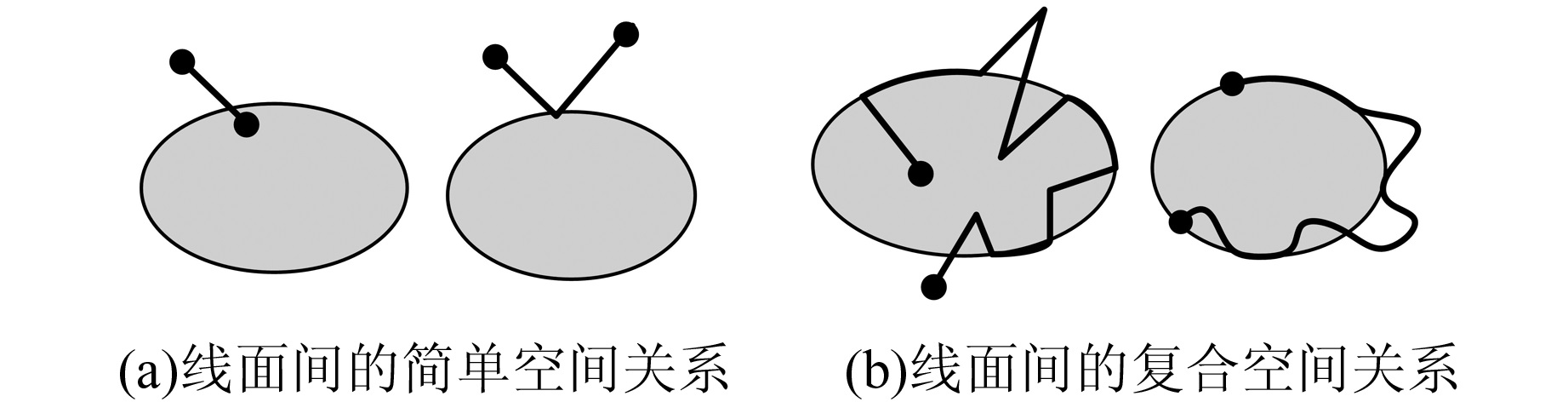
1 线面简单拓扑关系及其分类从理论上讲,线与面间的拓扑关系有无穷多种。原因如下:线与面之间可以有无穷多个交点,交点个数不同,拓扑关系不同[11];若考虑直线段集合的有序性和基本拓扑关系组合的任意性[14],顺序与组合方式不同,拓扑关系不同。线与面之间的关系可以非常简单,也可以非常复杂,如图1所示。
|
| 图 1 线面间的简单拓扑关系与复合拓扑关系 Fig. 1 Simple Topological Relation and Compound Topological Relation of Line-Region |
为了便于区分,对简单拓扑关系和复合拓扑关系进行定义[11]:
定义1 把线与面边界之间相交次数为0或1的拓扑关系称为简单拓扑关系。
定义2 把线与面边界之间相交次数大于1的拓扑关系称为复合拓扑关系。
1.1 线面简单拓扑关系根据线段端点与面边界的关系,可以把线面间的简单拓扑关系分为13种,如图2所示。下面证明其完备性。线与面之间基本拓扑关系的完备性可以按照线与面边界交集的维数来进行说明:

|
| 图 2 线面间的13种简单拓扑关系 Fig. 2 Thirteen Simple Topological Relations of Line-Region |
1) 若线与面边界之间没有交集,即交集的维数为-1,有且只有2种情况:如图2(1)与图2(2)所示;
2) 若线与面边界之间的交集为一个点,即交集维数为0,有且只有5种情况:如图2(3)~图2(7)所示;
3) 若线与面边界之间的交集为线,即交集维数为1,有且只有6种情况:如图2(8)~图2(13)所示。
因此,线与面之间有且仅有13种简单拓扑关系。
1.2 线面关系类型划分对线面的13种简单拓扑关系进一步地抽象和分类,本文给出以下定义。
定义3 面A与线L,当线L与面A边界的交集为空时,依据线L与面A内部的交集情况,可定义以下线L与面A的拓扑关系:
1) 若线L与面A内部的交集为空,则将其拓扑关系定义为相离;
2) 若线L与面A内部的交集不为空,则将其拓扑关系定义为包含。
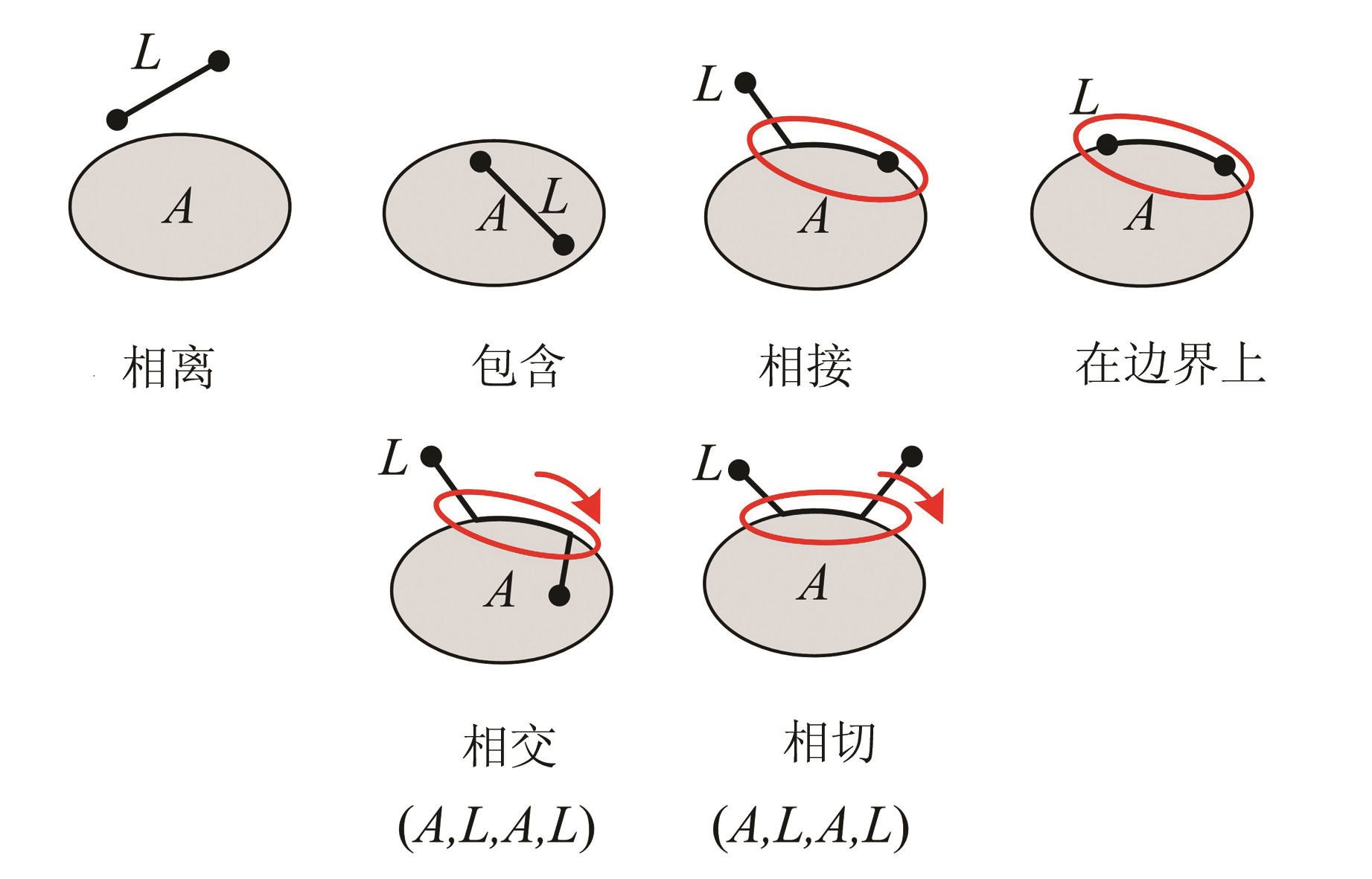
定义4 面A与线L,当线L与面A边界的交集不为空时,作线L与面A边界交集的邻域ε,则ε与线L及面A边界存在交点,如图3所示。依据交点数目及局部交顺序的差异,可定义以下线L与面A的拓扑关系:
|
| 图 3 线面间的简单拓扑关系类型 Fig. 3 Types of Simple Topological Relations of Line-Region |
1) 若交点数为2,则将其拓扑关系定义为在边界上;
2) 若交点数为3,则将其拓扑关系定义为相接;
3) 若交点数为4,有两种情况:
① 按顺时针或逆时针方向,若ε穿越A和L的顺序为交替进行,则将其拓扑关系定义为相交;② 按顺时针或逆时针方向,若ε穿越A或L连续两次,则将其拓扑关系定义为相切。
以上定义可以通俗地理解为:在线面关系中,当线与面发生接触时,若线的两个端点在面边界的同一侧,则为相切关系;若线的两个端点跨越了面边界,即在边界的两侧,则为相交关系;若线的一个端点位于面边界上,一个端点不在面边界上,则为相接关系。若线与面没有发生接触,则为相离或包含关系。由以上分析可知,本文的定义符合人的认知惯性,易于理解记忆。
另外,在线面发生接触的情况下,根据线与面边界交集的维数,相交有0维相交(0,C)和1维相交(1,C),相接有0维相接(0,M)和1维相接(1,M),相切有0维相切(0,T)和1维相切(1,T),叠置只有1维的情况(1,O),如图4所示。

|
| 图 4 线面边界交集的维数差异 Fig. 4 Differences of Line-Region Boundary Intersection |
1) 相离:图2(1)。
2) 相接。0维接:图2(3)和图2(4);1维接:图2(8)和图2(9)。
3) 相交。0维交:图2(5);1维交:图2(12)。
4) 包含:图2(2)。
5) 相切。0维切:图2(6)、图2(7);1维切:图2(10)、图2(11)。
6) 在边界上:图2(13)。
2 利用元拓扑关系的线面空间关系集成表达方法 2.1 元拓扑关系的概念和特点进一步分析发现,只有线与面发生接触时才有可能产生复合线面关系,包含与相离是不能构成复合线面关系的。而在发生接触的简单线面关系中,在边界上关系不能组成复合线面关系。因为在复合关系中,由于线与面连续多次发生接触,在边界上关系可以被1维相切关系或1维相交关系所包含。
因此,线与面间的复合关系只能由相交、相切和相接关系组成。据此,可以定义元拓扑关系。
定义5 把能够组成线面复合关系的、最小不可分的线面简单拓扑关系称为线面元拓扑关系。
不难发现,线面元拓扑关系有3类6种,即0维相交(C0)、1维相交(C1)、0维相切(T0)、1维相切(T1)、0维相接(M0)和1维相接(M1),如图5所示。

|
| 图 5 线面间的6种元拓扑关系 Fig. 5 Six Meta-relations of Line-Region |
元拓扑关系具有以下特点:
1) 概括性。概括性是指元拓扑关系必须概括所有复合关系的基本特征。也就是说,任意一个复合关系都可以由若干元拓扑关系按照一定的排序、经过有限次组合而成。元拓扑关系作为基本组成元素存在,必须能够概括复合关系的所有特征。
2) “基本”不可分性。“基本”不可分性,是指一般情况下,元拓扑关系就是组成复合拓扑关系的最小单元,不能再分。但元拓扑关系又不能太过于具体,否则会导致过多的繁琐工作,元拓扑关系必须在保证概括性的前提下,保证其不可分性。
另外,在组成复合拓扑关系时,相接关系还具有以下特点,如图6所示。

|
| 图 6 线面复合关系中的相接关系 Fig. 6 Meet of Line-Region Compound Topological Relations |
1) 对于相接关系来说,有且只有一个端点位于面的边界上,因此在复合拓扑关系中,相接关系的排序只能是1或者n。
2) 在线面复合拓扑关系中,相接关系的出现次数不超过2。
3) 在线面复合拓扑关系中,若出现相接关系,则线的首点或末点必然在面边界上。
2.2 元拓扑关系的方位在线与面边界发生接触时,线可能在面的外部,也可能在面的内部,这就涉及到线与面的内外方位问题。
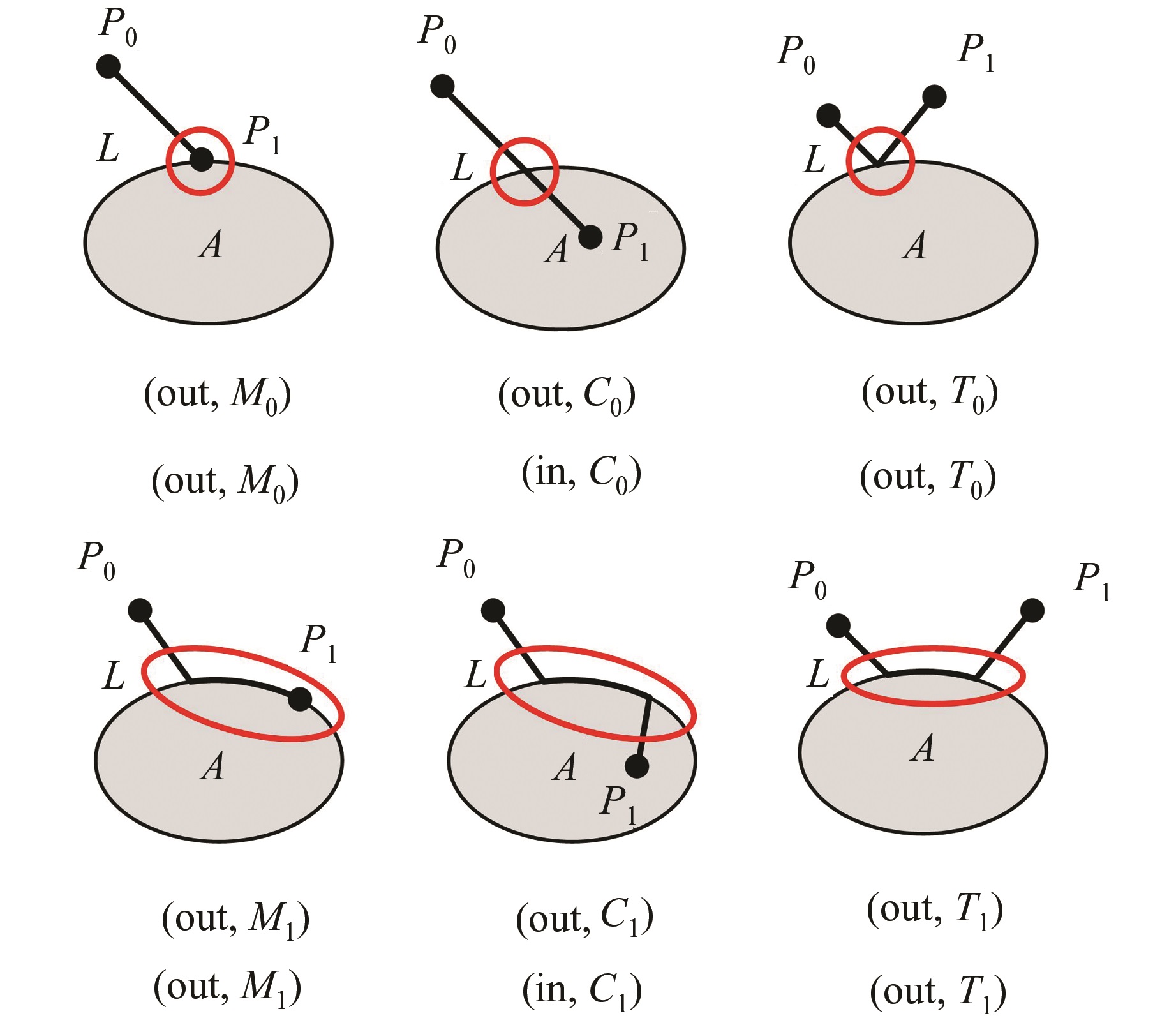
对于每个元拓扑关系来说,设线的两个端点为P0和P1,以P0为起始点,沿着L向P1前进,记下L与ε的第一个交点,若此交点在面A的内部,则记为in;在面A的外部,则记为out。当然,也可以以P1为起点进行描述。纳入方位关系以后,分别以P0和P1为起点,线面间的3类6种元拓扑关系可进一步详细描述如下(见图7)。
|
| 图 7 集成方位关系的线面元拓扑关系描述 Fig. 7 Description of Meta-relations with Integrated Position Relation |
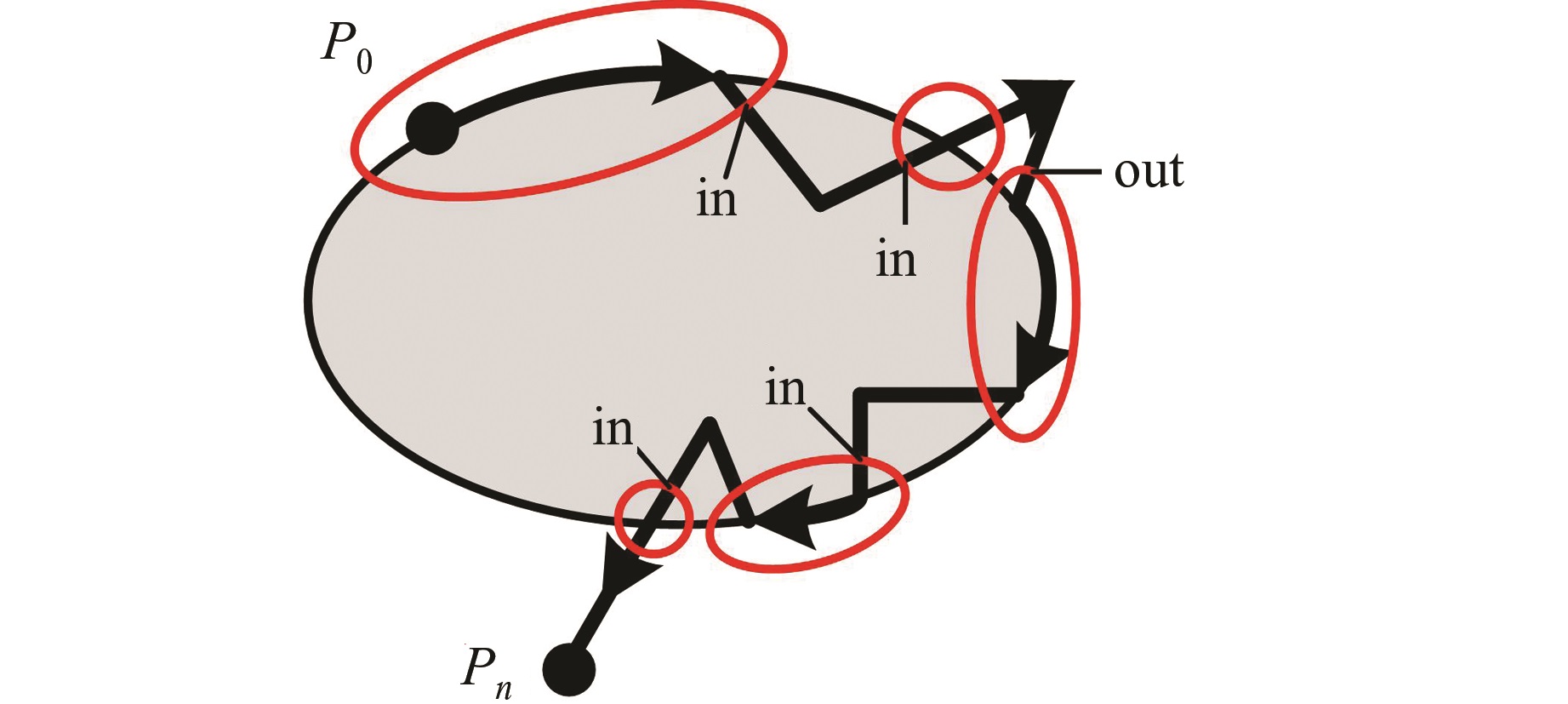
由于元拓扑关系的作用是组成复合拓扑关系,因此有必要对复合拓扑关系中元拓扑关系的方位问题进行说明。如图8所示的复合拓扑关系,箭头表示线的走向,椭圆表示每个元拓扑关系的邻域ε,短细线所指交点表示沿着线的走向,线与每个元拓扑关系ε的第一个交点。依据上述约定,可得出复合拓扑关系中每个元拓扑关系的方位(见图8)。
|
| 图 8 集成方位关系的复合线面拓扑关系描述 Fig. 8 Description of Compound Relations with Integrated Position Relation |
记əA为面A的边界,R(L,A)表示面A和线L的关系,有:
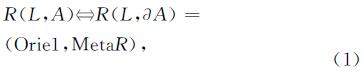

当线面交集为一维时,交集的方向不同,拓扑关系不同。交集方向可能为顺时针c或逆时针a,图9(1)和图9(4)、图9(2)和图9(5)、图9(3)和图9(6)中红色箭头所标示的元拓扑关系分别为交集方向不同的相交关系、相接关系、相切关系。
进一步纳入线面一维交分量的方向关系,有:

|
| 图 9 元拓扑关系一维交分量的方向 Fig. 9 Orientation of Meta-relation Intersection |

其中,Orie1=in,out,Orie2=c,a,

元拓扑关系的类型、内外方向、一维交分量的方向只是对元拓扑关系本身进行了约束,而元拓扑关系之间如何连接则需要连接顺序和连接方向的约束。
定义6 不妨设线L与面A边界之间有n个元拓扑关系(如图10所示),按以下步骤可以得到线L与面A复合关系的元拓扑关系连接序列,记为OrderəA。
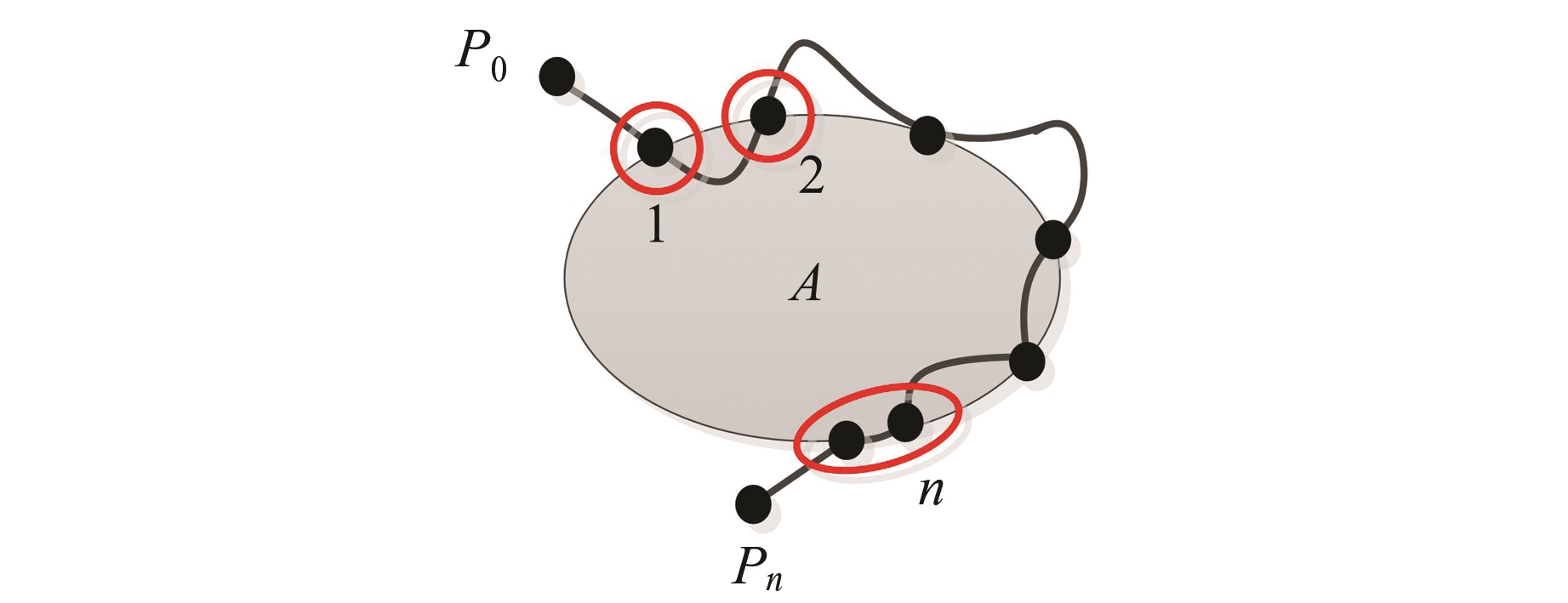
|
| 图 10 线面间的n个元拓扑关系 Fig. 10 n Meta-relations of Line-Region |
1) 设线L的两个端点为P0和Pn,以P0为起始点,沿着L向Pn前进,将L与A的交分量依次编号为1,2,3,…,n,其中n≥2。
2) 以面A的边界A为参考,从第1个元拓扑关系起,按顺时针方向跟踪,记下每个元拓扑关系的编号,直到最后一个元拓扑关系为止,则有:

进一步纳入元拓扑关系的连接顺序,有:
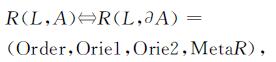
其中,Order=1,2,3,…n,Orie1=in,out,
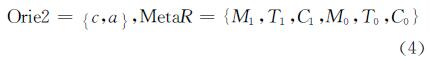
定义7 设线L与面A边界之间有n个元拓扑关系,第i个元拓扑关系的连接方向为第i个元拓扑关系与第i+1个元拓扑关系之间的连接线按线端点P0到Pn的走向,投影于此连接线相对应的面边线上的方向,第n个元拓扑关系没有方向,如图11箭头所示。

|
| 图 11 元拓扑关系的连接方向 Fig. 11 Connection Orientation of Meta-relations |
元拓扑关系的连接方向可能为顺时针或逆时针。元拓扑关系的连接方向能够进一步区分图11(1)和图11(2)~图11(4)之间的关系。
纳入元拓扑关系的连接方向,有:

每个交分量都对应一个元拓扑关系,因此,线L和面A的复合关系R(L,A)可以表示为:

其中,

按照式(6),图12中的复合拓扑关系可表示为:

|
| 图 12 线面复合关系 Fig. 12 Compound Relations of Line-Region |

分析该模型及以上实例,可得出以下特性: 按照序号由小到大的顺序分析,只有产生相交关系时才会发生方位关系的变化,即在复合关系矩阵中,只要遇到元拓扑关系C,下一个方位关系必然由in变为out或者由out变为in。若遇到的元拓扑关系为T或者M,则下一个方位关系不发生变化。这与元拓扑关系的定义也是相一致的。
因此,在模型中只需表示首交分量的方位关系,其他交分量的方位关系可依据上述分析推理得到。
据此可将将式(6)进一步化简,得到: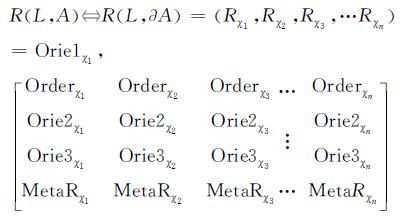

本文提出了空间关系集成表达模型的评价指标为:
1) 区分性。模型能否区分不同的空间关系。
2) 描述性。针对空间图形关系,能否给出形式化的描述。
3) 约束性。依据该形式化的描述,能否确定空间关系的具体图形形式,即澄清不同用户关于同一空间关系存在不同的语义理解问题。
3.2 线面空间关系集成表达模型的区分性本文提出的线面空间关系集成表达模型能够区分文献[11]中提出的较为特殊的4类线面复合关系以及文献[14]中的97种线面关系。
3.3 线面空间关系集成表达模型的描述性由于线L的首末点选择不同,同一线面关系图利用定性线面关系集成表达模型可以得到两种等价的描述结果。如图13所示的同一线面空间关系分别对应以下两种等价的描述结果:

|
| 图 13 同一线面关系线的首末点选择不同的两种情况 Fig. 13 Two Descriptions of the Same Line-Region Relation with Different Starting Points |

一种描述结果是否对应唯一线面关系?即依据描述结果,是否能够绘出且只能绘出一种线面关系图是要讨论的问题,假设描述结果如式(10)所示。依据描述结果绘制线面空间关系的步骤如下:
1) 元拓扑关系排序的确定。依据矩阵第1行的序号在面边界上确定元拓扑关系的排序。
2) 元拓扑关系形式的确定。依据元拓扑关系的Orie1(内外方位)、Orie2(一维交分量的方向)、元拓扑关系的类型,确定元拓扑关系的具体类型。例如第1个元拓扑关系的类型为T1(1维切),且在面的外面,1维切的方向为逆时针,据此可以绘制第1个元拓扑关系;第2个元拓扑关系的类型为C0(0维交),且依据定理1,可判断交的方向为out,即由外向内,据此可以绘制第2个元拓扑关系。自此,可以确定各个元拓扑关系的具体形式。
3) 元拓扑关系连接方式的确定。依据元拓扑关系的连接方向,即矩阵中的第4行,可以确定元拓扑关系的具体连接方式。例如,第1个元拓扑关系与第2个元拓扑关系以顺时针方式连接,第2个元拓扑关系与第3个元拓扑关系以逆时针方式连接,……自此,确定了元拓扑关系的连接方式,得到了线面复合拓扑关系图,如图14所示,与图13进行比较,可知空间关系是一样的。

|
| 图 14 依据描述结果还原线面空间关系的步骤 Fig. 14 Steps of Restoring the Line-Region Relations Based on the Description |
综上所述,本文提出的线面关系集成表达模型能够区分不同的空间关系;针对空间图形关系,能够给出形式化的描述;依据该形式化的描述,能够确定空间关系的具体图形形式,澄清不同用户关于同一空间关系存在不同的语义理解问题。即本文模型在区分性、描述性和约束性方面具有良好的表现。
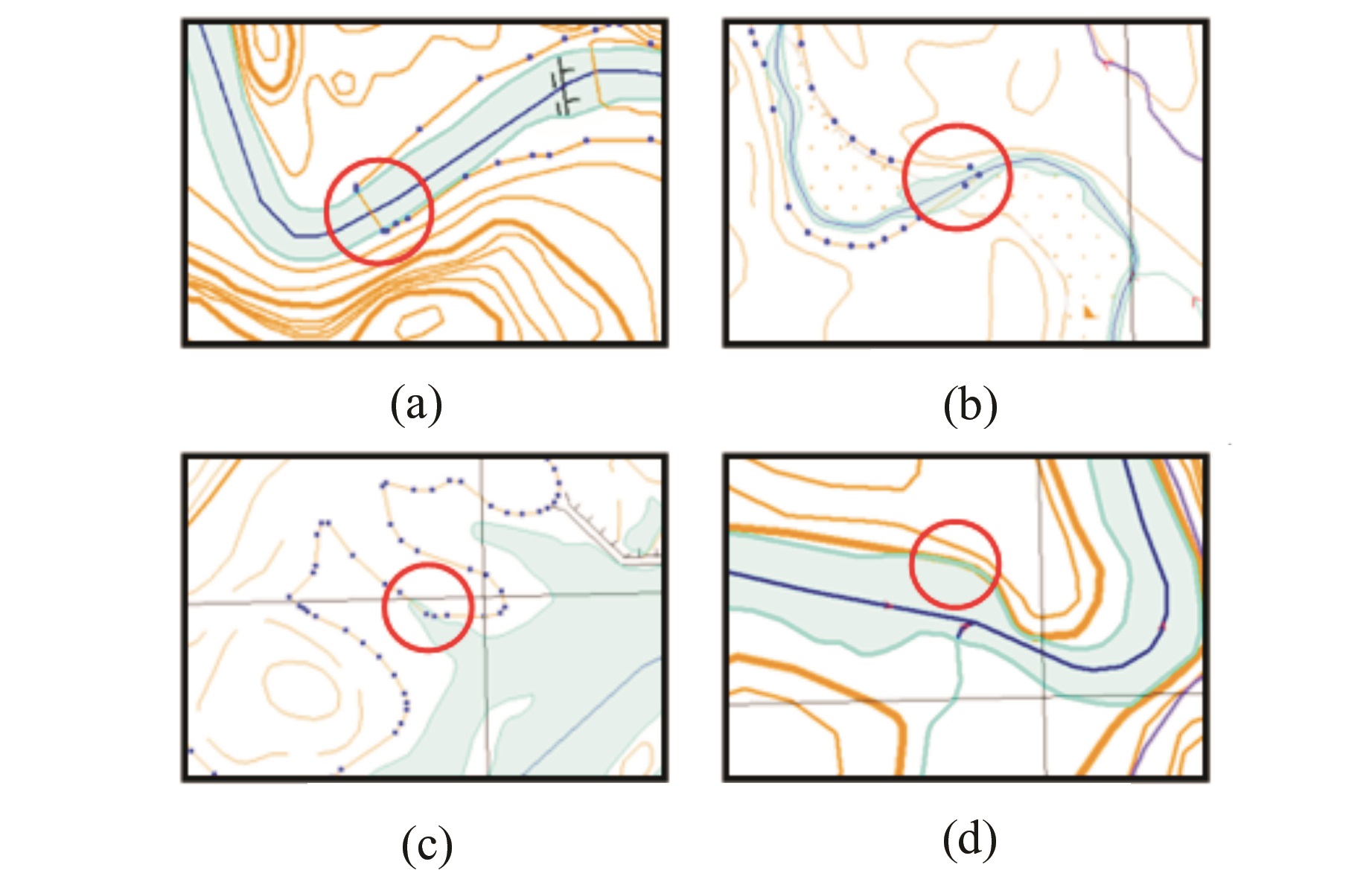
4 空间关系集成表达模型的应用本文提出的线面空间关系集成表达模型能够用于矢量地图数据的空间冲突检测。以等高线与面状水系的空间冲突为例,图15(a)中等高线近似垂直地穿越双线河,为正确的空间关系;图15(b)中等高线小角度穿越双线河,表示此处河流水面倾斜,为空间关系缺陷;图15(c)中等高线与河流小面积相交,很可能是作业员失误或者河流更新导致的错误,属于空间关系缺陷;图15(d)中等高线与面状水域的边线发生了重叠,违背了“水往低处流”的自然规律,属于空间关系缺陷。
|
| 图 15 等高线与面状水系之间的空间关系 Fig. 15 Spatial Relations Between Contour Lines and Region River |
在本文提出的集成表达模型的基础上,纳入度量关系(式(11)中的度量关系为面积关系,单位为mm2),对上述线面空间关系进行描述,可以得到以下结果:

将上述结果结合设定好的规则(见式(12)),其含义为:若等高线与面状水域之间的拓扑关系出现0维相交,且相交面积AOD<25,则有90%的几率出现j号等高线落k号水域面的缺陷。进行匹配比对,可以得出产生空间关系缺陷的结论。

本文的后续工作集中于以下方面:(1)采用本文提出的元拓扑关系,对线与多个面之间、线与复杂面之间,以及面面之间的复合拓扑关系集成表达方法进行研究;(2)结合度量参数,将其应用于矢量地图数据质量缺陷的自动识别。
| [1] | Chen Jun, Zhao Renliang. The Basic Problems and Research Progress of GIS Spatial Relationships[J]. Acta Geodaetica et Cartographica Sinica, 1999,28(2):95-102(陈军,赵仁亮. GIS空间关系的基本问题与研究进展[J]. 测绘学报,1999,28(2):95-102) |
| [2] | Deng Min, Li Chengming, Liu Xiaoli.Discuss of Several Basic Problems in the GIS Spatial Relationship Description[J]. Engineering Science, 2013,15(5):20-24 (邓敏,李成名,刘晓丽.论GIS空间关系描述中存在的几个基本问题[J].中国工程科学,2013,15(5):20-24) |
| [3] | Liu Wanzeng, Chen Jun, Deng Kazhong, et al.A Topology Chain Model for Describing Line-Line Spatial Relations[J]. Journal of China University of Mining & Technology, 2010,39(1):75-79 (刘万增,陈军,邓喀中,等. 线线空间关系描述的拓扑链模型[J].中国矿业大学学报,2010,39(1):75-79) |
| [4] | Chen Jun, Liu Wanzeng, Li Zhilin, et al. The Refined Calculation Method of Topological Relations between Line Objects[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(8):255-260(陈军,刘万增,李志林,等. 线目标间拓扑关系描述的细化计算方法[J].测绘学报,2006,35(8):255-260) |
| [5] | Zhai Renjian. Research of Multi-scale Vector Spatial Data Matching Method Based onGlobal Consistency[D].Zhenzhou:Information Engineering University,2011(翟仁健.基于全局一致性评价的多尺度矢量空间数据匹配方法研究[D].郑州:信息工程大学,2011) |
| [6] | Zhan Chensheng, Wu Fang, Zhai Renjian, et al. A Spatial Conflicts Detection Methods of Lines Based on Topological Consistency[J]. Journal of Geomatics Science and Technology, 2011,28(5):387-390 (詹陈胜,武芳,翟仁健,等.基于拓扑一致性的线目标空间冲突检测方法[J]. 测绘科学技术学报,2011,28(5):387-390) |
| [7] | Zhan Chensheng.Study on Automatic Detection of Spatial Conflict in Multi-scale Database[D]. Zhengzhou:Information Engineering University,2012 (詹陈胜.多尺度数据库中空间冲突自动检测方法研究:以线要素为例[D].郑州:信息工程大学,2012) |
| [8] | Deng Min, Li Zhilin, Li Yongli,et al. A Generic Model of Line-Line Topological Relations in GIS[J]. Geomatics and Information Science of Wuhan University, 2006, 31(11):945-949 (邓敏,李志林,李永礼,等.GIS线目标间拓扑关系描述的4交差模型[J].武汉大学学报·信息科学版,2006,31(11):945-949) |
| [9] | Egenhofer M J, Rashid A, Shariff B M. Metrics Details for Natural-Language Spatial Relations[J]. ACM Transaction on Information System, 1998, 16(3):1-29 |
| [10] | Lin Yan, Liu Wanzeng, Han Gang.A Method for Describing Topological Relations between Single Line Feature and Multi-Polygon Features[J]. Science of Surveying and Mapping, 2013, 38(2):128-131 (林艳,刘万增,韩刚. 一种单线与多面要素间的拓扑关系描述方法[J].测绘科学,2013,38(2):128-131) |
| [11] | Deng Min,Ma Hangying. The Hierarchical Representation of Topological Relations Between a Line and an Area[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(4):507-513(邓敏,马杭英.线与面目标间拓扑关系的层次表达方法[J]. 测绘学报,2008,37(4):507-513) |
| [12] | Deng Min, Li Zhilin, Qi Huabin. An Integrated Approach to Representing Line-line Spatial Relations in GIS[J]. Acta Geodaetica et Cartographica Sinica, 2007,36(4):421-427 (邓敏,李志林,祁华斌.GIS线目标间空间关系的集成表达方法[J].测绘学报,2007,36(4):421-427) |
| [13] | Deng Min, Li Zhilin, Li Yongli.A Hierarchical Approach to Line-Line Topological Relations in GIS[J].Journal of Remote Sensing,2007,11(3):311-317 (邓敏,李志林,李永礼.GIS线目标间拓扑关系描述的层次方法[J].遥感学报,2007,11(3):311-317) |
| [14] | Guo Qingsheng, Chen Yujian, Liu Hao. Spatial Topolotical Relationships Combination Reasoning of Line and Region[J]. Geomatics and Information Science of Wuhan University, 2005,30(6):529-532 (郭庆胜,陈宇箭,刘浩. 线与面的空间拓扑关系组合推理[J]. 武汉大学学报·信息科学版,2005,30(6):529-532) |
 2016, Vol. 41
2016, Vol. 41


