文章信息
- 刘坡, 龚建华
- LIU Po, GONG Jianhua
- 大规模遥感影像全球金字塔并行构建方法
- Parallel Construction of Global Pyramid for Large Remote Sensing Images
- 武汉大学学报·信息科学版, 2016, 41(1): 117-122
- Geomatics and Information Science of Wuhan University, 2016, 41(1): 117-122
- http://dx.doi.org/10.13203/j.whugis20130718
-
文章历史
- 收稿日期: 2014-09-11

2. 中国科学院遥感与数字地球研究所, 北京, 100039
2. State Key Laboratory of Remote Sensing Science, Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100101, China
随着摄影测量和遥感技术发展,遥感数据质量不断提高,数据量呈现爆炸式增长,而且这个趋势在未来仍将继续下去[1],如何共享和可视化这些数据仍然是一个挑战。虚拟地球的出现给人们提供了一个新的基于网络的互操作和可视化工具,目前广泛应用于空间数据共享、服务和辅助决策支持等[2, 3, 4]。常用的虚拟地球平台有World Wind,Google Earth、OSGEarth等,特别是World Wind,作为一个开源软件,支持影像、地形、矢量和三维模型的加载,可以作为一个理想的大规模遥感数据可视化平台[5],本文的算法主要在World Wind上实现。
金字塔模型是虚拟地球中海量遥感影像可视化的基础[6],它是一种多分辨率层次模型,在保证显示精度的前提下,不同区域通常采用不同分辨率的数据来提高渲染速度。金字塔的构造过程本质就是对影像进行分块和分层处理[7],尽管增加了总的数据量,但能够减少完成绘制所需的总时间。金字塔模型广泛应用于二维地图的可视化,通过对原始数据进行重采样,可以明显提高渲染的速度。由于采样顺序的不同,重采样可以分为自底向上和自顶向下两种方法。自顶向下方法是从原始图像开始,逐级采样得到更低分辨率的图像,最终得到最低分辨率的图像;而自底向上方法则是首先采样得到最低分辨率的图像,再逐渐采样次低分辨率的图像,需要大量的内存来存储数据。这种串行计算方法一般只适合于小规模的数据,对于大规模数据处理效率不高。如 20 G 大小的原始数据重采样生成的瓦片大小为256 像素×256 像素,总的瓦片容量大约有27 G,用传统的串行算法大约需要5 h,而且在普通的计算机上很难实现。
构造金字塔的过程主要包括数据重采样和瓦片存储,并行算法可以提高计算的速度。传统的并行算法主要是通过集群CPU来提高计算的效率,但是该方法并没有充分发挥单个计算机的并行计算能力,同时集群需要巨大的硬件成本。图形处理器(graphics processing unit,GPU)的出现意味着并行计算时代的来临,普通计算机上的显卡都具有GPU加速能力。GPU 主要起源于数值模拟和分析[8, 9, 9],随着技术的发展,它逐渐运用于地学领域,如空间分析、空间聚类等[10, 11]。GPU技术特别适合于规则分布的遥感数据处理,其已经广泛应用于遥感图像的特征提取、匹配、分类和插值采样等费时的计算[1213, 14, 15, 16]。对于金字塔构建,文献[17]提出了一种基于阈值的CPU和GPU 金字塔创建算法,利用阈值选择CPU或者GPU 来完成数据的采样。但是该方法没有考虑数据经常超出内存的容量和大量小瓦片的存储问题。本文充分运用GPU和多线程技术,通过GPU来加速重采样点的计算,采用多线程技术来完成数据的存取,以此加速全球遥感影像金字塔的构建。
本文策略主要包括:(1)二级数据分解策略(磁盘到CPU、CPU 到GPU),克服内存和显存的限制;(2)构造四叉树模型,减少在显存和内存之间传输数据的次数;(3)充分发挥GPU多线程并行处理的性能;(4)采用多线程策略加速数据传输的过程。
1 全球遥感影像金字塔构建 1.1 全球剖分网格在虚拟地球平台中,主要采用全球剖分网格模型。它从[-180°,-90°]开始(对应经度和纬度),对全球进行规则网格划分,并对每块瓦片进行唯一编码。全部数据都转换为WGS84坐标,从而实现在统一平台下多源空间数据的集成和可视化。假设原始图像的分辨率为 ro,像素矩阵大小为W×h,对数据采样之后的瓦片大小为 d × d,则瓦片矩阵的大小 tr×tc。其中,tr=int(w/d),tc=int(h/d),int为向下取整,LD表示 0 层瓦片的范围(单位为°)。可以依据原始数据大小和分辨率计算出构造金字塔的级数N,N满足:
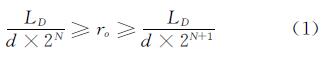
在构造金字塔的过程中,需要对影像进行重采样,常将每2×2个像素合成为 1 个像素,对于第l级的分辨率为rl为:
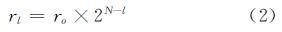
第l层的像素矩阵大小为 trl×tcl,其中,trl=int[w/(d×2l)],tcl=int[h/(d×2l)]。假设x和y分别表示某点的纬度和经度,则该点所在l 级的瓦片的编码为:
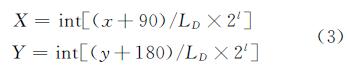
构造金字塔需要对影像进行重采样,常用的方法有最邻近采样法、双线性内插法和三次卷积内插法[18]。三次卷积插值消除了最邻近插值算法的锯齿走样问题,也解决了双线性插值的边缘模糊问题,但其复杂的计算也导致了运算量的急剧增加,本文直接对原始的影像进行合并处理。
1.2 数据传输在构造金字塔的过程中存在大量的数据传输,主要包括原始数据读取、瓦片存储及内存和GPU中的数据交换,在整个程序运行过程中占有很大的比例。图1 表示不同大小的图像采用最邻近法采样为256像素×256 像素大小的图像时,数据传输时间占数据处理总时间的百分比。从图1可以看出,随着像素尺寸的扩大,数据传输所占的比例逐渐减少。数据传输的比例从512 k大小的50%,下降到128 M的30%。由此可见,数据传输在数据重采样过程中占有很大的比例。

|
|
图 1 传输时间比例
Fig. 1 Percent of Total Time for Transferring of Resampling Different Size Image |
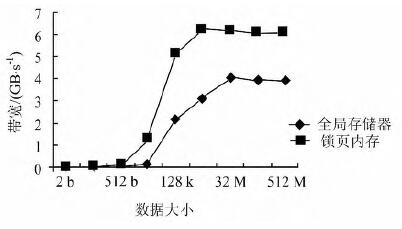
GPU架构的内存模型主要包括全局存储器、共享存储器、寄存器、纹理存储器或常量存储器。常用的是全局存储器和共享存储器,但是全局存储器中数据有400~800个时钟周期延迟。图2表示在实验机器上的带宽测试,在主机的内存和显存之间使用CudaMemcpy API 传输数据,通过全局存储器,可以得到3.9 GB/s的持续带宽,而通过PCIe接口可将分页锁定的数据传输到显存中,并可以获得5.9 GB/s的带宽。可以看出,在数据量小于8 kB的时候,与采用锁页内存相比较,全局存储器大约有0.05 ms的延迟。这部分的时间在数据量较小,或者计算量比较小的时候,对程序有严重的影响。当数据大于8 kB之后,带宽会有明显的提高,当数据量大于 2 MB以后,设备带宽达到稳定的状态,分别达到3.9 GB/s、5.9 GB/s。本文通过地址映射实现了从GPU直接访问主机端锁页内存,实现了对内存数据的零拷贝,可以明显地提高计算速度。
|
| 图 2 带宽测试 Fig. 2 Host-Device Bandwidth Measurements |
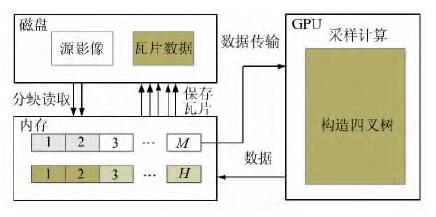
图3表示了并行金字塔构建框架,主要的流程为:(1)通过二级数据处理策略来突破内存和显存的限制,首先读取磁盘文件中合适大小的数据到内存中缓存,并通过锁页内存传输到显存中进行下一步的处理;(2) 在GPU中完成采样计算,并将采样获得的数据以构造四叉树的结构组织起来,整体传输出显存;(3)在内存和磁盘之间采用多线程策略进行读取和存储数据。图中M表示一次可以传输进显存的数据的大小的数目,H表示M块影像生成的瓦片数据的数目。
|
| 图 3 并行全球金字塔构造 Fig. 3 Parallel Construction of Global Pyramid |
假设影像数据包含N×N 像素,其中N=2k,对应级别为k,不足的地方可以用空值填充。假设 k层中每2×2个像素合成一个像素,生成第k-1 级图像,依次类推,直到生成0级图像,为1个像素。其中,k-1个像素矩阵的大小分别为N/2×N/2、N/4×N/4和1×1。除了原始数据之外,重采样后的金字塔的像素数M 为:
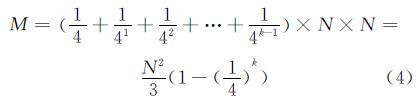
由于显存和内存的容量限制,对于20 GB的影像,串行算法很难构建金字塔。如果采用自顶向下的采样方法,每次都要调用最高一层的影像生成第一级影像,需要的内存都为20GB;而对于自底向上的方法,从最高级开始,依次生成低一级的影像金字塔。假设生成9级金字塔,如表1所示,第9级数据瓦片的总容量为20 GB,而第8级为5 GB,随着级数的降低,数据量不断减少。
| 级数 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 容量 | 80 kB | 320 kB | 1.25 MB | 5 MB | 20 MB | 80 MB | 320 MB | 1.25 GB | 5 GB | 20 GB |
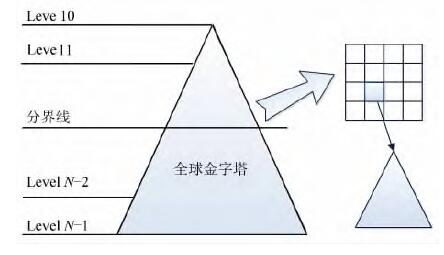
本文采用二级分解策略来克服内存不能一次性读取数据的问题,在构造金字塔的过程中,一般根据影像的大小来设置构造金字塔的起始层(对应图4中的分界线)。假设生成的瓦片大小为256像素×256像素,大约为128 kB,高一级别的每4个像素合并为低一级别的一个像素,对应的第4级的瓦片大小为128像素×128像素。从表1可以看出,第0~4级影像瓦片总的大小约为27 MB。为了减少数据的输入和输出量,低于5级的瓦片可以全部存储到内存中,对应于第9级的大小为32 MB,原始图像可以生成第5级上的一个256像素×256像素的瓦片。同时,加上在内存中的0~4级图像,总的瓦片大小大约27 MB,则每次运算所需的最小内存容量仅为59 MB。当每个瓦片生成完毕之后,再进行下一个瓦片的处理,直到所有的瓦片都处理完毕之后,再统一生成0~4级上的瓦片。通过本文方法,每次只需要很少的内存就可以实现大规模数据的金字塔构建。
|
| 图 4 大规模数据的二级分解策略 Fig. 4 Two Level Decomposition Strategies of Lager Data |
金字塔构建最终的瓦片为256像素×256像素的数据,其大小约为128 kB。对于这样的小文件,全局存储器的延迟会有重要的影响。在CPU环境下,可以把相关的文件链接为指针,但是由于GPU 不支持动态内存和指针,本文将相关的小文件组合,统称为构造四叉树,最大化消除数据在GPU和内存中传输延迟的影响。
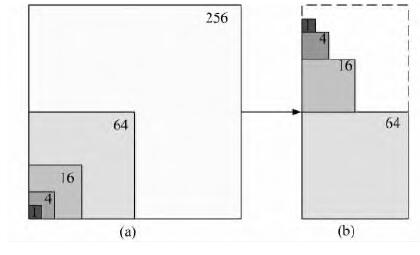
图5(a)所示的为一个16×16 像素大小的影像,可以建立5级金字塔,其大小分别为1、4、16、64、256个像素,对应的层级为0、1、2、3、4级。图5(b)所示为构造四叉树的结构,将采样之后的金字塔瓦片按照图示的位置存放,待所有的采样都完成之后,一次性传输到内存中进行编码,并存储到文件中。此时需要对GPU总采样之后生成数据进行编码。假设影像数据包含N×N像素,K表示采样的最大的级别,如图5(b)所示,构造四叉树的左下角的坐标为(0,0),左上角的坐标为 (0,N/2),右下角的坐标为 (N/2,0),则第0级左下角坐标为(N/2,0),第1级左下角的坐标为(0,0),右上角坐标为(N/2,N/2),则对于r级数据,其左下角像素的编号为:
|
| 图 5 构造四叉树 Fig. 5 Constructing Quadtree |
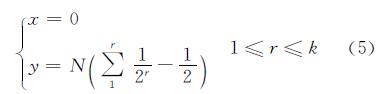
本文在GPU中采用全局内存来完成采样计算,同步进行所有级别的图像采样计算,并将计算结果放到构造四叉树的对应位置,直到完成所有的计算为止。然后将结果数据输出到内存中,采用多线程策略将生成的数据瓦片存储到磁盘中。
2.4 存储阈值如前所述,空间数据的内存和显存都存在阈值,假设显存的阈值为T GB,输入显存的数据为M GB,构造四叉树的大小为M/2 GB,则M的大小满足:

假设内存的阈值为D GB,则磁盘中输入到内存中的原始数据的大小为N GB,由于采用多线程策略,则数据大小为2N GB,分界级别层的数据大小为Nthreshold GB,则N的大小满足:

实验采用GeForce GT630显卡,显存容量为2 GB,计算能力为2.1,时钟频率为1.50 GHz,有12个流多处理器,每个流多处理器中有8个流处理器,计算机处理器为2.5 GHZ Quad-core,物理内存大小为4 GB。 实验在32位Windows 7系统下,采用VS 2010.net编程环境,利用CUDA Toolkit 5.0工具包开发。主要采用GDAL读取和存储瓦片数据,数据切分后每块瓦片的大小为像素,实验对不同大小的原始数据进行测试。数据主要包括1 GB(18 918×18 918像素,24位真彩色)和5 GB(42 303×42 303像素,24位真彩色)数据,同时也对10 GB(2块5 GB的图像)、15 GB(3块5 GB的图像)和20 GB(4块5 GB的图像)大小的影像数据进行了测试。
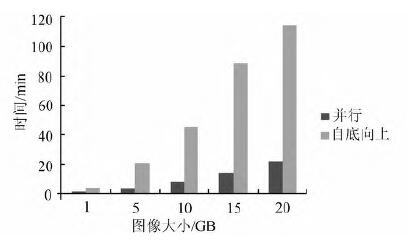
3.1 速度比较由于实验机器内存的限制,很难实现自顶向下的采样。采用分块的方法,当数据超过内存大小的时候,采用分块的方式进行读取,自底向上逐步建立金字塔,再与本文提出的并行构建方法进行比较,本文中分界层的级别取需采样数据的总级别的1/2。在GPU处理中用锁页内存传输数据,采用多线程策略在磁盘中读取和存储数据。图6表示不同的方法重建金字塔所花费的时间。从图6中可以看出,并行重采样速度比自底向上的处理速度要快,加速比平均可达到6倍,而且随着数据的越来越大,加速越明显。
|
| 图 6 不同大小的影像构造时间 Fig. 6 Runtime of Two Construction Method for Different Images |
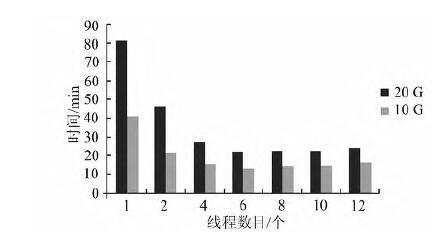
多线程的数目和金字塔构造的速度密切相关,因为存在大量的离散的小文件,小文件的输入和输出成为影响算法一个重要的因素。图7表明,随着线程的增加,总的处理时间也逐渐降低。但是当线程的数目为6时,计算速度开始变慢。多线程的数目应根据不同的计算机硬件配置进行设置。
|
| 图 7 线程数目对金字塔构造的影响 Fig. 7 Impact of Thread Configure to Parallel Construction |
本文针对大规模遥感影像全球金字塔构建问题,提出了一种并行构建算法,通过二级分解策略来突破CPU和磁盘传输的瓶颈;在数据传输过程中,利用锁页内存来克服GPU和CPU的传输延迟,并采用多线程策略来降低瓦片存储的时间;在GPU采样过程中,通过构造四叉树最大化地重用显存中的数据,从而最少化I/O的次数。总之,可以通过较低的内存和显存,实现大规模遥感影像数据的全球金字塔构建。实验结果表明,与传统的串行处理策略相比,可以显著提高遥感数据处理的速度,而且算法不受数据量大小的限制。本文算法同样可以适用于地形金字塔的构建。由于金字塔构建过程中生成了大量的小瓦片,小瓦片拷贝是一个费时的工作,如何对小瓦片进行组合,形成一个大文件,从而加快文件拷贝的速度,将是下一步研究的重点。
| [1] | Goodchild M F, Guo H, Annoni A, et al. Next-Generation Digital Earth[J]. The National Academy of Sciences, 2012, 109(28):11 088-11 094 |
| [2] | Brovelli M A, Zamboni G. Virtual Globes for 4D Environmental Analysis[J]. Applied Geomatics, 2012, 4(3):163-172 |
| [3] | Turk F J, Hawkins J, Richardson K, et al. A Tropical Cyclone Application for Virtual Globes[J]. Computers & Geosciences, 2011, 37(1):13-24 |
| [4] | Chien N Q, Keat T S. Google Earth as a Tool in 2-D Hydrodynamic Modeling[J]. Computers & Geosciences, 2011, 37(1):38-46 |
| [5] | Tooth S. Virtual Globes:a Catalyst for the Re-enchantment of Geomorphology?[J]. Earth Surface Processes and Landforms, 2006, 31(9):1 192-1 194 |
| [6] | Deng X. Research on Service Architecture and Algorithms for Grid spatial Data[J]. Acta Geodaetica et Cartographica Sinaca, 2003, 36(4):362-367(邓雪清. 栅格型空间数据服务体系结构与算法研究[J]. 测绘学报,2003, 36(4):362-367) |
| [7] | Viola I, Kanitsar A, Groller M E. Hardware-Based Nonlinear Filtering and Segmentation Using High-Level Shading Languages[M]. New York:IEEE Computer Society, 2003 |
| [8] | Xie J, Yang C, Zhou B, et al. High-Performance Computing for the Simulation of Dust Storms[J]. Computers, Environment and Urban Systems, 2010, 34(4):278-290 |
| [9] | Walsh S D, Saar M O, Bailey P, et al. Accelerating Geoscience and Engineering System Simulations on Graphics Hardware[J]. Computers & Geosciences, 2009, 35(12):2 353-2 364 |
| [10] | Zhang Y, Liu P, Yang M. Accelerating Bipartite Graph Co-Clustering Based on GPU[J]. Geography and Geo-Information Science, 2013, 29(4):99-103(张宇,刘坡,杨敏华.基于GPU的二部图联合聚类并行算法研究[J].地理与地理信息科学,2013, 29(4):99-103) |
| [11] | Zhang J, You S. CudaGIS:Report on the Design and Realization of a Massive Data Parallel GIS on GPUs[C]. The Third ACM SIGSPATIAL International Workshop on GeoStreaming, Redondo Beach, California, USA,2012 |
| [12] | Zhang B, Yang W, Gao L, et al. Real-Time Target Detection in Hyperspectral Images Based on Spatial-Spectral Information Extraction[J]. Eurasip Journal on Advances in Signal Processing, 2012, 2012(1):1-15 |
| [13] | Steinbach M, Hemmerling R. Accelerating Batch Processing of Spatial Raster Analysis Using GPU[J]. Computers & Geosciences, 2012, 45:212-220 |
| [14] | Giannesini F, Le Saux B. GPU-accelerated One-Class SVM for Exploration of Remote Sensing Data[C]. 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany,2012 |
| [15] | Yang C, Wu H, Huang Q, et al. Using Spatial Principles to Optimize Distributed Computing for Enabling the Physical Science Discoveries[J]. The National Academy of Sciences, 2011, 108(14):5 498-5 503 |
| [16] | Xiao H, Zhou Q, Zhang Z. Parallel Algorithm of Harris Corner Detection Based on Multi-GPU[J]. Geomatics and Information Science of Wuhan University, 2012, 37(7):876-881 (肖汉, 周清雷, 张祖勋. 基于多GPU的Harris角点检测并行算法[J].武汉大学学报·信息科学版,2012, 37 (7):876-881) |
| [17] | Kang J, Du Z, Liu R. Parallel Image Resample Algorithm Based on GPU for Land Remote Sensing Data Management[J]. Journal of Zhejiang University(Science Edition), 2011, 38(6):695-700(康俊锋, 杜震洪, 刘仁义, et al. 基于GPU加速的遥感影像金字塔创建算法及其在土地遥感影像管理中的应用[J]. 浙江大学学报(理学版), 2011, 38(6):695-700) |
| [18] | Parker J A, Kenyon R V, Troxel D E. Comparison of Interpolating Methods for Image Resampling[J]. IEEE Transactions on Knowledge and Data Engineering, 1983, 2(1):31-39 |
 2016, Vol. 41
2016, Vol. 41


