文章信息
- 于合理, 郝金明, 刘伟平, 谢建涛, 张辉
- YU Heli, HAO Jinming, LIU Weiping, XIE Jiantao, ZHANG Hui
- 一种卫星钟差异常实时监测算法
- A Real-Time Anomaly Monitoring Algorithm for Satellite Clock
- 武汉大学学报·信息科学版, 2016, 41(1): 106-110
- Geomatics and Information Science of Wuhan University, 2016, 41(1): 106-110
- http://dx.doi.org/10.13203/j.whugis20130812
-
文章历史
- 收稿日期: 2013-12-23

时间系统是卫星导航定位的核心要素之一,高精度的定位测量,归根结底都是高精度的时间测量。星载原子钟是星上的时间基准,决定了卫星导航定位和时间频率传递的精度,但卫星钟十分敏感,很容易受到太空环境的影响而发生复杂的变化,严重时会导致无法用于卫星导航定位[1]。无论是从系统的完好性还是从用户安全的角度来考虑,都需要对卫星钟的完好性进行监测。卫星钟的完好性监测主要是监测卫星钟差异常,可以通过星载原子钟的高精度频率或相位比对测量、动态Allan方差和基于滑动窗口的最小二乘拟合算法来实现[1, 2, 3, 4]。这些算法可以监测不同的卫星钟差异常情况,但在实时性上,它们还很难满足实时定位系统的要求[4],如在基于区域参考站网络的实时精密单点定位系统中,需要在估计钟差的同时实时对各卫星钟差进行异常检测,并对钟差异常数据进行剔除与替换。本文在对卫星钟差建模的基础上,提出了一种基于递推遗忘因子最小二乘算法(RFFLS)的卫星钟差异常实时监测算法,并进行了实验分析。
1 卫星钟差异常监测算法 1.1 卫星钟差预报模型卫星钟差的异常检测需要建立较为准确的卫星钟差模型,卫星钟频率具有足够的稳定性,一般采用二次多项式模型[5, 6, 7, 8]:
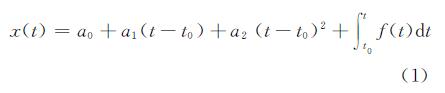
式中,a0表示卫星在参考时刻t0时的钟差;a1表示钟速;a2表示钟速变化率;∫tt0f(t)dt为随机相对频率误差。式(1)可以表示为矩阵形式:

式中,X为n维观测向量;a为3维未知参数向量;e为n维误差向量;H为n×3维设计矩阵。
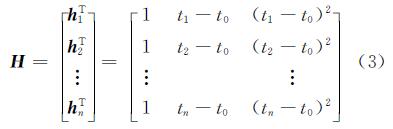
可得最小二乘解:
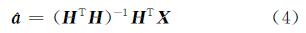
利用式(4)解算卫星钟差模型参数时,采用的观测值权矩阵是单位阵,即将新老数据统一对待,但对于预报而言,离预报时刻越近的观测数据与后续预报结果的相关性越强,对预报钟差的贡献也越大。因此,在解算钟差模型参数时,观测值权矩阵不应采用单位阵[9]。为了加强新数据对预报模型的贡献,削弱老数据的影响,本文引入遗忘因子矩阵作为观测权矩阵。遗忘因子取不同的值就可以得到不同的遗忘效果[9]。若已知遗忘因子为λ,则遗忘因子矩阵W为:

在采用一般最小二乘算法预报卫星钟差时,随着观测数据的增多,会造成数据包饱和,降低参数估计的性能,显然不能用以前的全部观测量进行卫星钟差的实时预报,通常的处理方法采用实时更新的一定长度的钟差数据对卫星钟差进行拟合预报[10]。但此方法显然没有充分利用钟差历史信息,为充分利用钟差历史信息,并加强当前数据的影响,提高钟差实时预报效率,本文采用递推遗忘因子最小二乘算法来预报卫星钟差。其基本思想是:当获得一个新数据时,不是将新数据加到老数据里重新进行计算,而是根据新数据对原估计量进行修正,得到新的改正后的估计量,再利用新的估计量进行预报,大大提高了估算效率。利用递推遗忘因子最小二乘算法拟合预报钟差的流程如下。
1) 利用m个数据(m≥3)计算拟合参数âm和Tm。
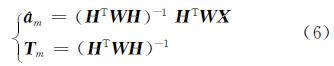
2) 根据式(7)迭代计算并存储k时刻的âk、Tk。

其中,k=m+1,m+2,…,n。
3) 计算则tk时刻钟差预测值:

1) 建立卫星钟差模型,利用递推遗忘因子最小二乘算法实时预报卫星钟差。
2) 计算统计检验量及监测门限,判断是否发生异常。
若实时解算钟差为xtk,则可构造统计检测量z:

若预报钟差的均方根误差为σpre,解算钟差xtk均方根误差为σsolve。则z的方差σ2满足式(10):

取z作为统计检测量,z服从均值为零、方差为σ2的正态分布。当没有异常发生时,系统处于正常的监测状态,若系统检测告警则是误警。若给定误警概率PFA,有概率公式为:
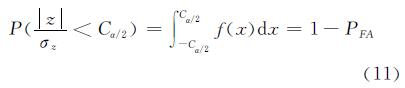
由式(11)可得检测门限T:

将实时计算的统计监测量z与钟差门限T进行比较。若z>T,则认为钟差异常并及时报警;若z≤T,则认为钟差数据无异常。
3) 若判定钟差数据无异常,则利用正常的钟差数据,实时更新递推遗忘因子最小二乘模型;若钟差数据异常,则对钟差异常数据进行剔除,并利用实时输出的预报钟差代替异常值对钟差预报模型进行更新,预报下一历元,从而完成异常数据的替换。
2 实验与分析为了验证本文方法的有效性,采用IGS网站提供的2012年1月27日的事后精密卫星钟差产品进行实验分析,数据采样间隔为30 s。考虑到目前GPS卫星原子钟有4种类型,随机选取不同类型的4颗卫星进行实验[10]。本文选取9号IIA铯钟、14号IIR铷钟、17号IIR-M铷钟及32号IIA铷钟进行实验。
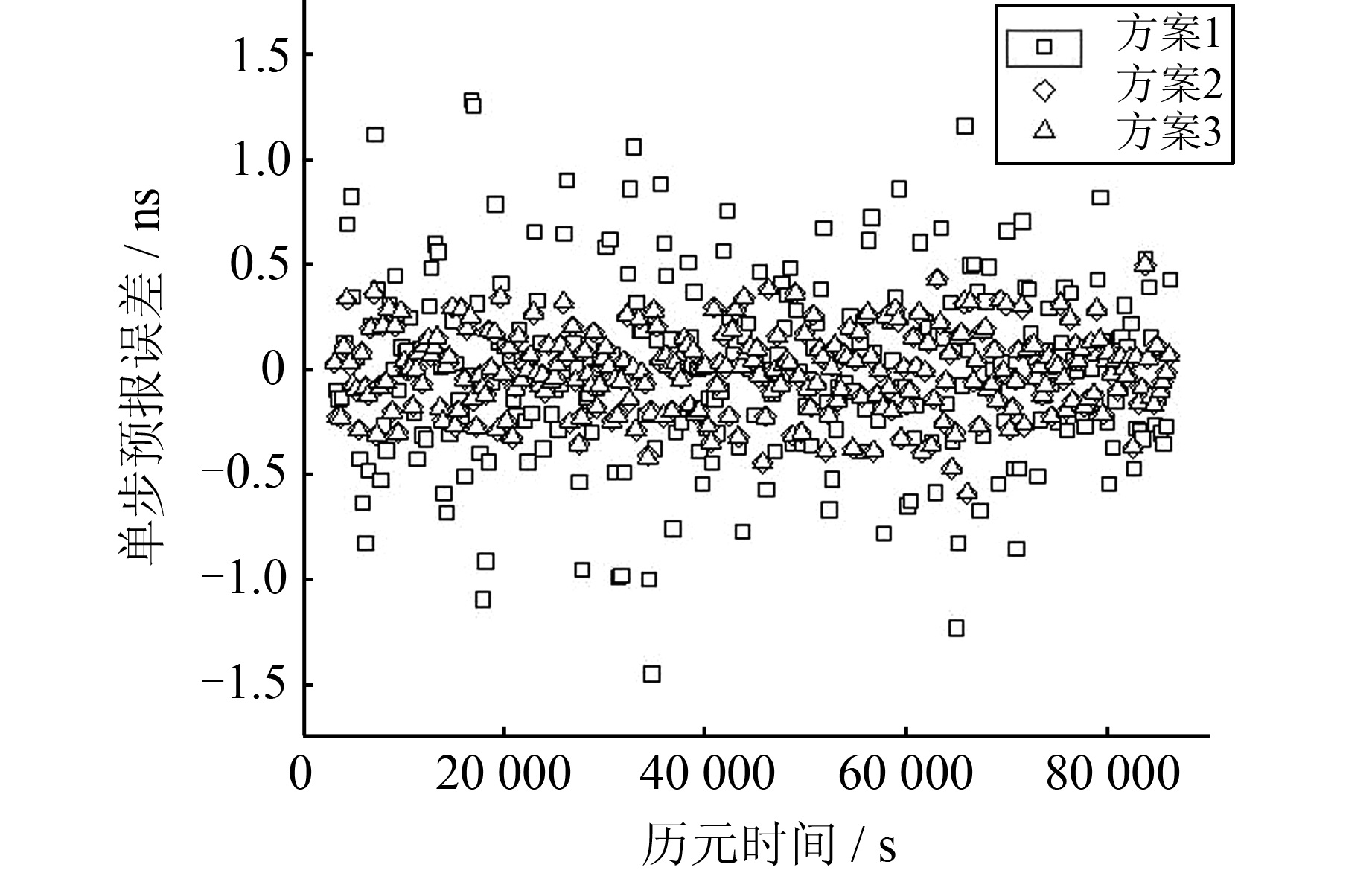
2.1 卫星钟差预报性能分析采用三种方案对卫星钟差预报情况进行分析,方案1和方案2均固定实时更新数据的长度为100,方案3计算初始参数的数据长度也设为100。为了能在图上清楚的显示,以五分钟数据间隔画图,图1~图4分别给出了9号、14号、17号和32号4颗卫星采用三种方案的卫星钟差预报误差图,表1给出了三种方案对4颗卫星钟差的预报精度。
|
| 图 1 9号卫星钟差预报误差 Fig. 1 Prediction Error of PRN09 |
|
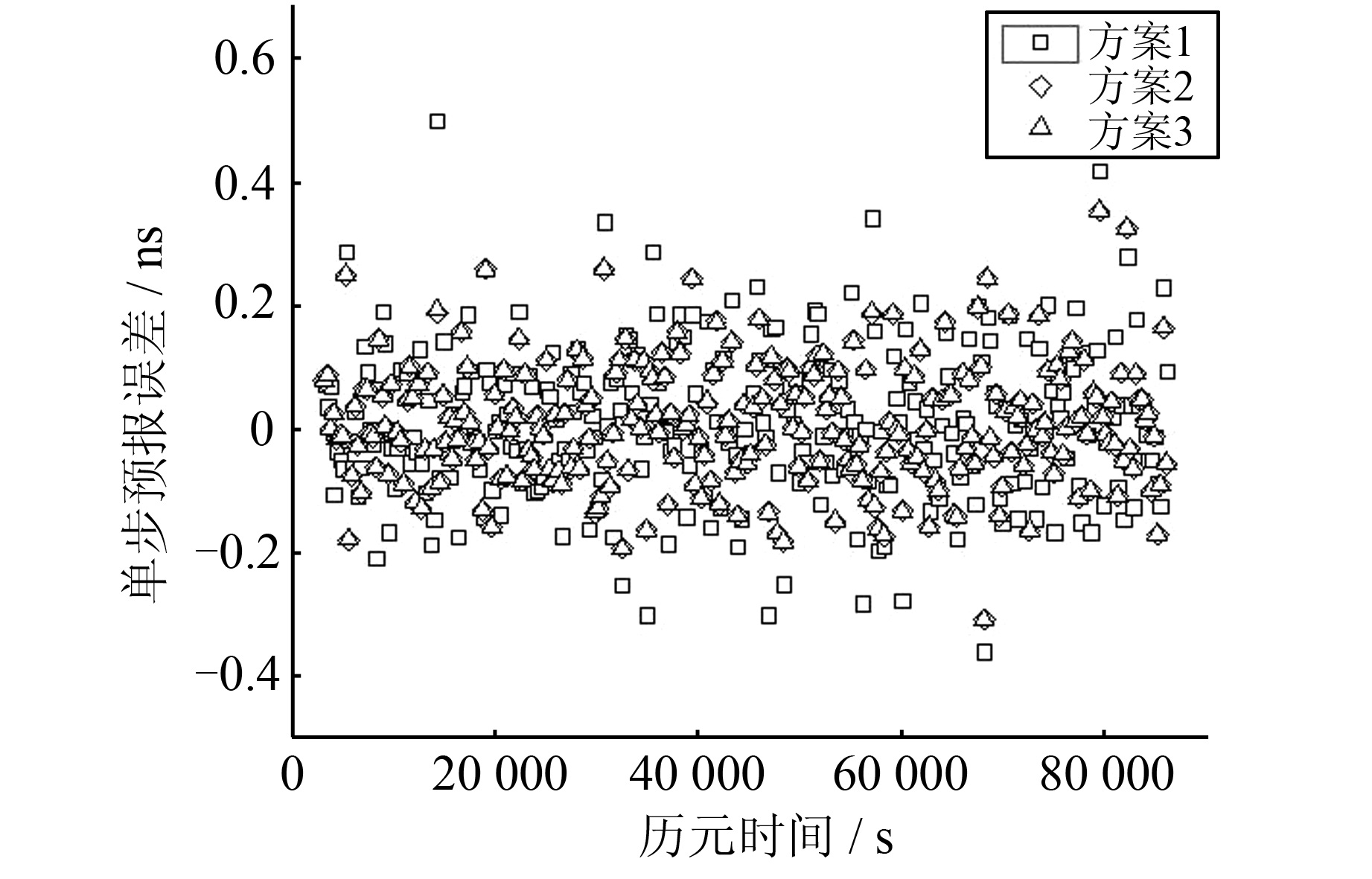
| 图 2 14号卫星钟差预报误差 Fig. 2 Prediction Error of PRN14 |
|
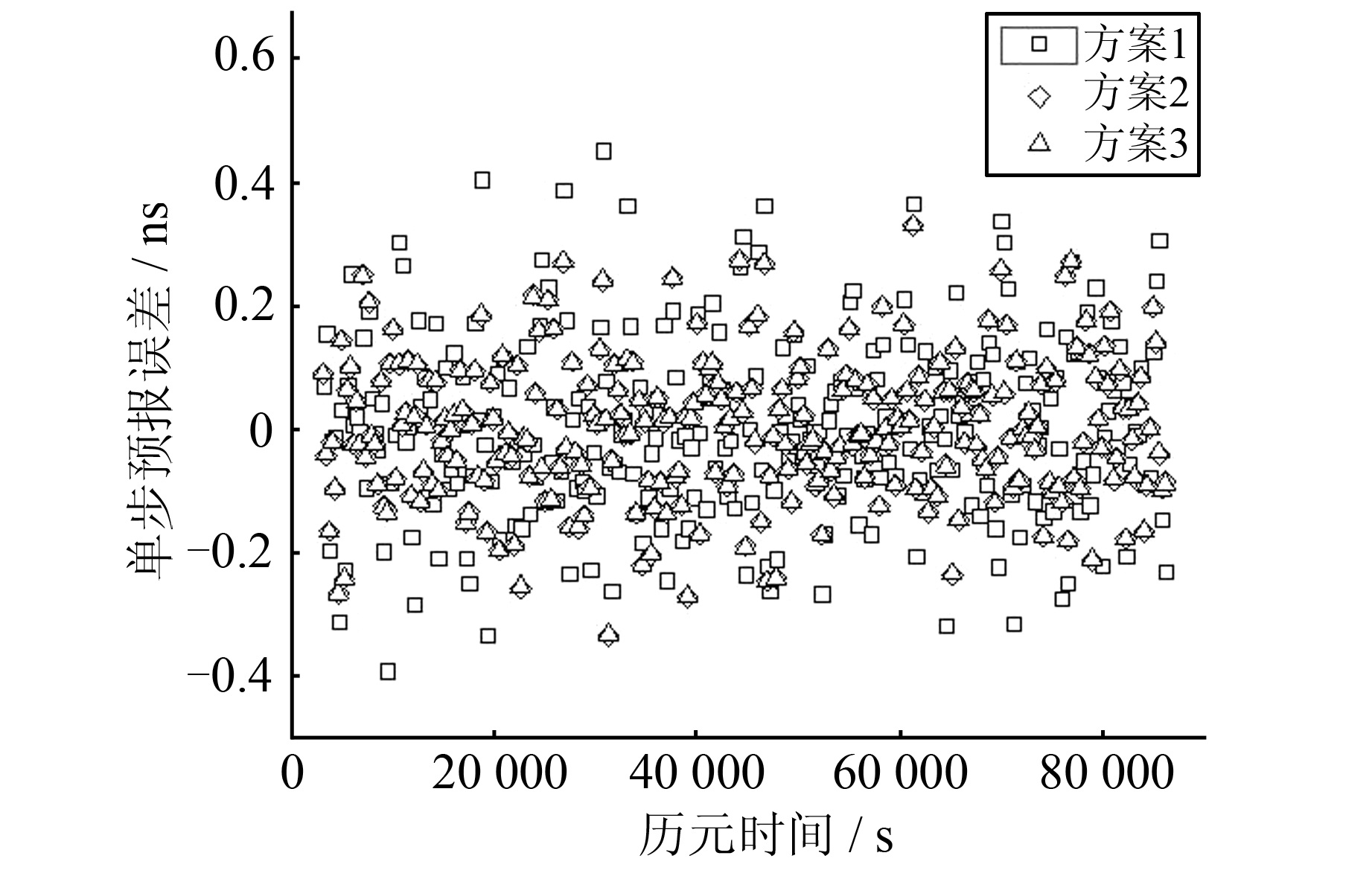
| 图 3 17号卫星钟差预报误差 Fig. 3 Prediction Error of PRN17 |
|
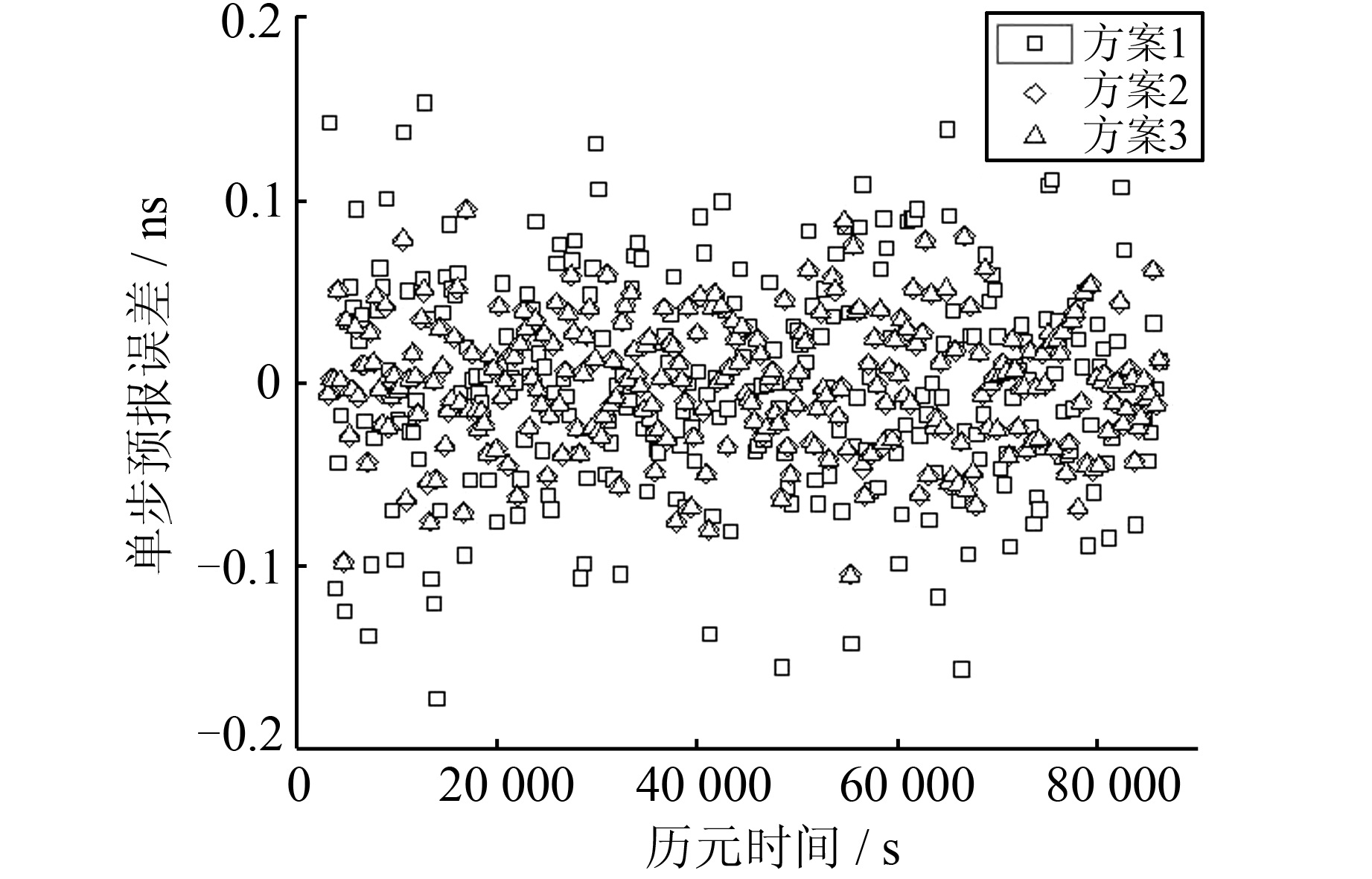
| 图 4 32号卫星钟差预报误差 Fig. 4 Prediction Error of PRN32 |
| PRN | 方案1 | 方案2 | 方案3 |
| PRN09 | 0.425 7 | 0.190 0 | 0.190 4 |
| PRN 14 | 0.119 4 | 0.099 6 | 0.099 5 |
| PRN 17 | 0.145 6 | 0.118 0 | 0.117 9 |
| PRN 32 | 0.060 6 | 0.031 4 | 0.031 5 |
方案1 利用实时更新的长度一定的钟差数据,采用最小二乘算法(LS)实时预报卫星钟差。
方案2 利用实时更新的长度一定的钟差数据,采用遗忘因子最小二乘算法(FFLS)实时预报卫星钟差。
方案3 采用递推遗忘因子最小二乘算法(RFFLS)实时预报卫星钟差。
由图1~图4和表1可知,同一方法不同卫星的预报精度并不相同,但原子钟性能较好的14号和17号卫星的预报精度还没有稳定性较差的32号卫星预报精度高,这主要是因为在这种小样本的超短期钟差预报中,预报钟差的精度虽然与卫星钟的稳定性有关,但更主要的是取决于卫星钟钟差在该时段内的小尺度变化[11]。对同一卫星而言,RFFLS算法和FFLS算法的钟差预报精度基本相当,并优于LS算法。尤其是对9号和32号卫星,采用RFFLS算法和FFLS算法的钟差预报精度明显优于LS算法,可以将预报精度从0.43 ns、0.06 ns分别提高到0.19 ns、0.03 ns。考虑到这两颗卫星分别为IIA铯钟和IIA铷钟,且都已工作20 a以上,卫星钟的稳定性相对较低,从而可以得出结论:卫星钟稳定性越差,RFFLS算法和FFLS算法相对于LS算法对钟差预报精度提高越明显,越能体现出这两种方法的优越性。
实验发现不同卫星采用相同方法预报钟差所用的时间基本一致,表2给出了利用1月27日1 d的数据,采用三种方案计算2 780个历元预报钟差所用的总时间及单历元平均耗时。
| 统计量 | 方案1 | 方案2 | 方案3 |
| 总耗时 | 8 119 | 8 084 | 740 |
| 平均耗时 | 2.92 | 2.91 | 0.27 |
由表2可知,RFFLS算法预报耗时还不到LS算法和FFLS算法的十分之一,仅为0.27 ms,预报效率明显高于LS算法的2.92 ms和FFLS算法的2.91 ms。显然,RFFLS算法比较适用于实时应用。
综上可知,综合考虑卫星钟差预报精度和计算耗时,RFFLS算法明显优于LS算法和FFLS算法,具有计算速度快、波动相对较小的特点。虽然相较于FFLS算法,RFFLS算法理论上并不是十分严密,但实验证明其预报钟差具有很高的精度,且大大提高了算法的效率,因此,应当采用方案3预报卫星钟差,进而对卫星钟差进行异常监测。
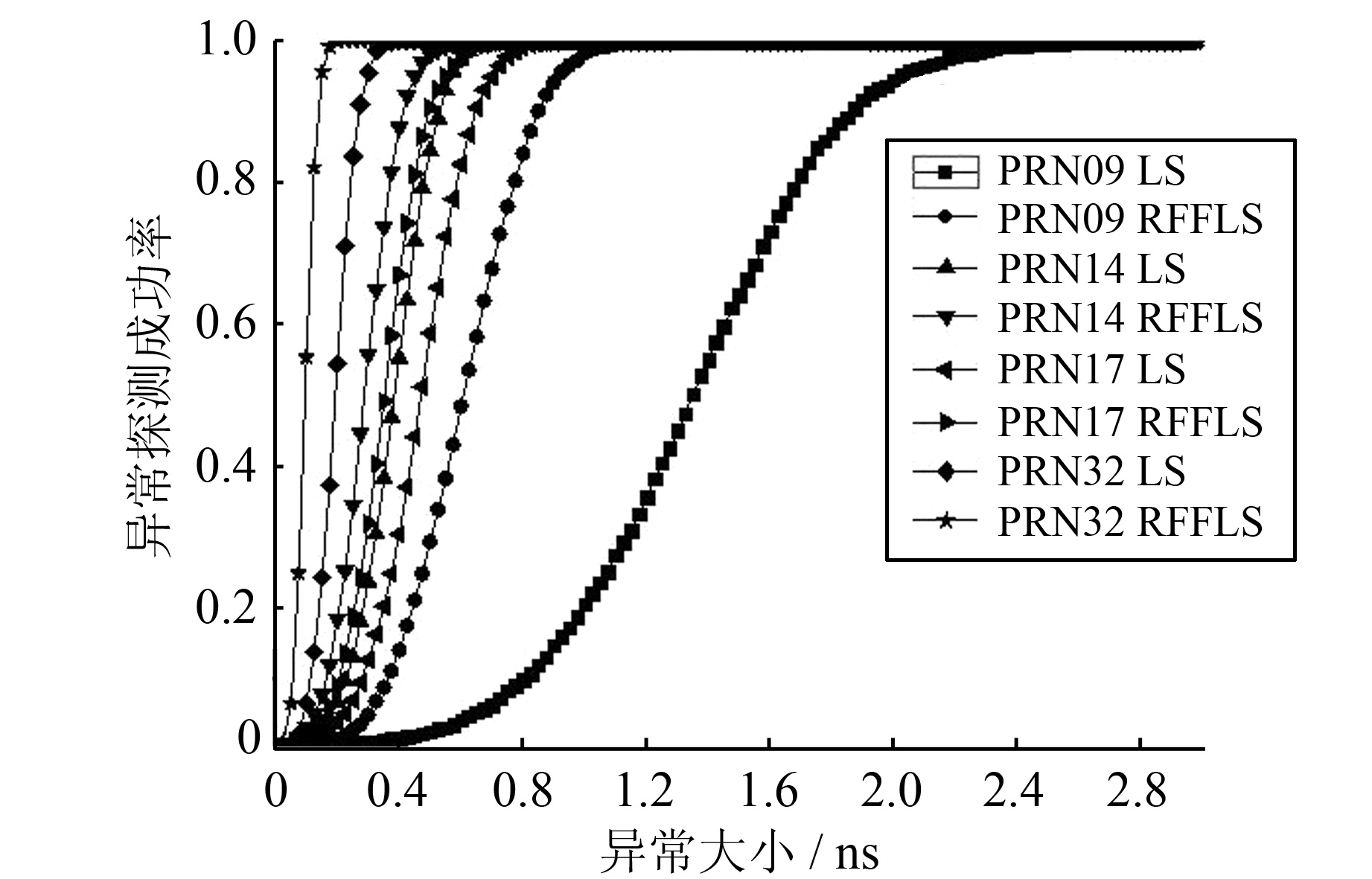
2.2 卫星钟差异常监测性能分析由卫星钟差异常监测原理可知,卫星钟差异常监测的能力主要取决于卫星钟差的预报精度。由前文分析可知,对于同一钟差数据,采用RFFLS算法和FFLS算法钟差预报精度基本一致,因此本文只分析RFFLS算法和LS算法的钟差异常监测能力。由于钟差异常数据不常见,为便于分析,人为地给IGS事后精密钟差加入误差来仿真钟差异常情况。误警概率取为1/15 000,计算1 d数据,统计能够准确探测出异常的百分比。图5给出了9号、14号、17号和32号4颗卫星采用两种方法探测出钟差异常的成功率随加入的钟差异常值大小的曲线变化图。
|
| 图 5 卫星钟差异常探测统计曲线 Fig. 5 Statistic of Anomaly Monitoring Results |
从图5可以看出,随着加入钟差异常值的不断增大,钟差异常检测成功率也明显增大。当探测成功率达到99%时,采用RFFLS算法,9号、14号、17号和32号4颗卫星能探测出的最小异常为1.025、0.525、0.650、0.175;采用LS算法,4颗卫星能探测出的最小异常为2.325、0.650、0.80、0.350。显然,对于同一颗卫星,采用RFFLS算法的钟差异常监测能力明显高于LS算法,尤以9号卫星明显,能够将钟差异常监测能力从2.325 ns提高到1.025 ns。
3 结 语实时定位系统中,不仅要求提供实时精密卫星钟差产品,还应当实时提供钟差完好性信息,因此需要实时对卫星钟差异常进行监测。本文提出基于递推遗忘因子最小二乘方法预报钟差,实现了卫星钟差异常监测的完好性算法,并对比分析了LS算法、FFLS算法和RFFLS算法的卫星钟差预报精度、预报耗时和对卫星钟差异常的监测性能,得出了RFFLS算法钟差预报精度和预报耗时均优于LS算法、RFFLS算法钟差异常监测能力明显高于LS算法的结论。
致谢:感谢全球连续监测评估系统(IGMAS)信息工程大学分析中心对本文工作的支持和帮助。
| [1] | Niu Fei, Han Chunhao, Zhang Yisheng,et al. Analysis and Detection on Atomic Clock Anomaly of Navigation Satellites[J]. Geomatics and Information Science of Wuhan University,2009, 34(5):585-588(牛飞, 韩春好, 张义生, 等. 导航卫星星载原子钟异常监测分析[J]. 武汉大学学报·信息科学版,2009,34(5):585-588) |
| [2] | Tang Sheng, Liu Ya, Li Xiaohui. A Study on Onboard Satellite Atomic Clock Autonomous Integrity Monitoring[J]. Journal of Astronautics, 2013,34(1):39-45(唐升, 刘娅, 李孝辉. 星载原子钟自主完好性监测方法研究[J]. 宇航学报,2013,34(1):39-45) |
| [3] | Rodriguez I, Garcfa C, Catalán C, et al. Satellite Autonomous Integrity Monitoring (SAIM) for GNSS Systems[C]. ION GNSS, Savannah, GA,2009 |
| [4] | Huang Xinming, Gong Hang,Zhu Xiangwei, et al. A Real-Time Anomaly Monitoring Algorithm for Satellite Clock Based on Kalman Filter[J]. Journal of Astronautic Metrology and Measurement, 2011,31(5):6-11(黄新明, 龚航, 朱祥维,等.基于Kalman滤波器的卫星钟实时异常监测算法[J].宇航计测技术,2011, 31(5):6-11) |
| [5] | Xu Longxia, Li Xiaohui. A Receiver Clock Bias-Based GPS RAIM Algorithm[J]. Journal of Astronautics, 2011, 32(3):537-542(许龙霞, 李孝辉. 基于接收机钟差的GPS完好性自主检测算法[J]. 宇航学报, 2011,32(3):537-542) |
| [6] | Mao Yue, Chen Jianpeng, Dai Wei, et al. Analysis of On-board Atomic Clock Stability Influences[J]. Geomatics and Information Science of Wuhan University, 2011, 36(10):1 182-1 186 (毛悦, 陈建鹏, 戴伟,等.星载原子钟稳定性影响分析[J]. 武汉大学学报·信息科学版,2011,36(10):1 182-1 186) |
| [7] | Lu Xiaofeng, Yang Zhiqiang, Jia Xiaolin, et al. Parameter Optimization Method of Gray System Theory for the Satellite Clock Error Predicating[J]. Geomatics and Information Science of Wuhan University, 2008,33(5):492-495(路晓峰, 杨志强, 贾小林, 等. 灰色系统理论的优化方法及其在卫星钟差预报中的应用[J]. 武汉大学学报·信息科学版,2008,33(5):492-495) |
| [8] | Wang Yupu, Lv Zhiping, Chen Zhengsheng, et al. Research on the Algorithm of Wavelet Neural Network to Predict Satellite Clock Bias[J]. Acta Geodaetica et Cartographica Sinica,2013,42(3):323-330(王宇谱, 吕志平, 陈正生, 等.卫星钟差预报的小波神经网络算法研究[J]. 测绘学报, 2013,42(3):323-330) |
| [9] | Song Cheng, WangXuefei, Zhuang Zhaowen. A Method for GPS Receiver Clock Offset Prediction Based on the Forgetting Factor Least Squares[J]. Science of surveying and Mapping,2008,33:41-43(宋成, 王雪飞, 庄钊文. 基于遗忘因子最小二乘的GPS接收机钟差预测算法研究[J]. 测绘科学, 2008,33:41-43) |
| [10] | Huang Guanwen. Research on Algorithms of Precise Clock Offset and Quality Evaluation of GNSS Satellite Clock[D]. Xi'an:Chang' an University, 2012(黄观文. GNSS星载原子钟质量评价及精密钟差算法研究[D]. 西安:长安大学,2012) |
| [11] | Yu Heli, Hao Jinming, Liu Weiping, et al. Model Analysis on Satellite Clock Error Ultra Short Term Prediction[J]. Journal of Geodesy and Geodynamics, 2014,34(1):161-164(于合理, 郝金明, 刘伟平,等.卫星钟差超短期预报模型分析[J]. 大地测量与地球动力学,2014, 34(1):161-164) |
 2015, Vol. 41
2015, Vol. 41


