文章信息
- 李晓杰, 郭睿, 黄金, 朱陵凤, 谭红力, 董恩强
- LI Xiaojie, GUO Rui, HUANG Jin, ZHU Lingfeng, TAN Hongli, DONG Enqiang
- 神经网络在北斗导航卫星轨道预报中的应用
- Application of Artificial Neural Network to Orbit Prediction of BeiDou Navigation Satellites
- 武汉大学学报·信息科学版, 2015, 40(9): 1253-1258
- Geomatics and Information Science of Wuhan University, 2015, 40(9): 1253-1258
- http://dx.doi.org/10.13203/j.whugis20130603
-
文章历史
- 收稿日期: 2013-10-26
2. 北京市遥感信息研究所, 北京, 100192
2. Beijing Institute of Remote Sensing Information, Beijing 100192, China
为彻底克服地面测轨监测网的有限地理分布问题,我国全球导航系统中提出了采用星间链路测距和星间时间同步的测轨模式来增强仅依赖有限分布地面监测网的星地链路定轨模式,其目的是提升北斗卫星导航系统的指标。对于无地面站支持的情况,中高轨位的导航卫星需要进行星上自主定轨,因此需要精度较高的轨道长期预报结果作为星上自主定轨的先验信息,如果先验值精度太差,可能导致定轨发散[1]。因此,高精度的轨道预报精度问题是制约我国全球卫星导航系统自主定轨精度的关键因素。
改进轨道预报精度,一种方法是通过分析卫星在空间所受的摄动力产生的物理原理,建立更加精准的动力学模型[2, 3, 4, 5, 6, 7],但此方法周期长,难度大[8, 9, 10, 11]。
改进轨道预报精度的另一种方法可以从轨道预报误差的规律中寻找突破[12, 13]。神经网络在处理非线性、高维性的问题时不需要准确知道输入输出函数的结构参数,只要通过训练来掌握他们之间的内在联系关系,并且在输入训练集以外的数据时,神经网络可以获得正确的映射关系。文献[14]根据GPS卫星星历的相关周期特性,利用神经网络建立预报模型,在没有任何动力学模型的情况下得到精度为一个星期数百米的预报结果。但是,由于将卫星位置量直接作为神经网络的输出,神经网络的状态量动态范围大,限制了预报精度的提高。文献[15]利用GPS卫星精密星历已知的优势,将神经网络与动力学模型相结合组成混合预报模型,改进GPS导航卫星的中长期预报,该方法可以在一定程度上改进轨道预报精度,但不是每次改进均能成功,存在改进失效的情况。
相比已有的针对GPS卫星的轨道预报精度改进算法,北斗系统中相关研究存在以下难点:一是精密星历的获取。对于GPS卫星,可以采用IGS精密星历作为基准轨道[16],而北斗导航卫星目前最长只有3 d的精密星历。二是北斗卫星导航系统采用GEO/IGSO/MEO的混合星座,卫星类型多,而GPS系统采用的单一的MEO卫星,相比而言,需要研究不同类型卫星的轨道预报算法。
1 中长期轨道预报的方案设计本文主要采用BP神经网络算法,它是一种多层网络的“逆推”学习算法[17, 18]。其基本思想是,学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时,输入样本从输入层传入,经隐层逐层处理后传向输出层。若输出层的实际输出与期望输出不符,则转向误差的反向传播阶段。误差的反向传播是将输出误差以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。这种信号正向传播与误差反向传播的各层权值调整过程周而复始地进行。权值不断调整的过程也就是网络的学习训练过程。此过程一直进行到网络输出的误差减少到可以接受的程度,或进行到预先设定的学习次数为止[19, 20, 21]。
为了缩小神经网络输出量的动态范围,本文采用预报误差而不是直接利用预报轨道作为训练样本。
建模分为训练和补偿两阶段。在训练阶段,采用拼接方法得到一条长时间的精密轨道,用于衡量动力学模型预报误差及神经网络模型的训练误差。某初始时刻的卫星轨道信息通过动力学模型采用数值积分外推得到预报轨道(X0,V0,T0),与精密轨道的重叠弧段对比结果为轨道预报误差ΔX0(T0),将其作为神经网络的训练样本;预报轨道(X0,V0,T0)作为神经网络的输入,预报误差ΔX0作为神经网络的理想输出,训练的目的在于让神经网络掌握他们之间的映射关系式,即要构造函数g(X,V,T)使之逼近满足下式关系的f(X0,V0,T0):
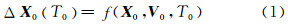
其中,函数f(X0,V0,T0)即为训练后的神经网络模型。
在补偿阶段,将当前时刻的预报轨道作为神经网络模型的输入,利用函数f(X,V,T)计算得到神经网络模型的输出作为当前时刻预报轨道的补偿值ΔXNN(T):
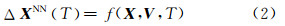
其中X、V分别为当前时刻预报轨道的位置矢量、速度矢量;ΔXNN(T)为该预报轨道对应的预报误差补偿矢量。
利用补偿矢量ΔXNN(T)修正当前时刻的预报轨道,得到最终的预报轨道:

其中, (T)为修正后预报轨道的位置矢量;X(T)为原始的预报轨道;ΔXNN(T)为预报轨道的补偿值。
(T)为修正后预报轨道的位置矢量;X(T)为原始的预报轨道;ΔXNN(T)为预报轨道的补偿值。
利用人工神经网络进行样本训练时,对训练样本的前提要求是连续、规律性强。本文将轨道预报误差作为训练样本,故要求轨道预报误差连续,这就要求有一条长期、连续的精密轨道作为基准轨道。而在目前的定轨技术范畴内,无法通过一次定轨得到覆盖长期弧段的基准轨道。本文提出采用拼接方法得到轨道精度相对较高的基准轨道,但发现轨道拼接处存在米级跳跃。跳跃的量级取决于定轨的精度,IGS星历的精度为厘米级,故其精密轨道的跳跃量级在厘米级。由于轨道预报误差为神经网络的学习样本,精密轨道跳跃会引起预报误差的不连续,影响神经网络的学习效果,一个连续光滑的学习样本序列才能保证模型的外推效果,故首先需要对轨道预报误差进行平滑处理。
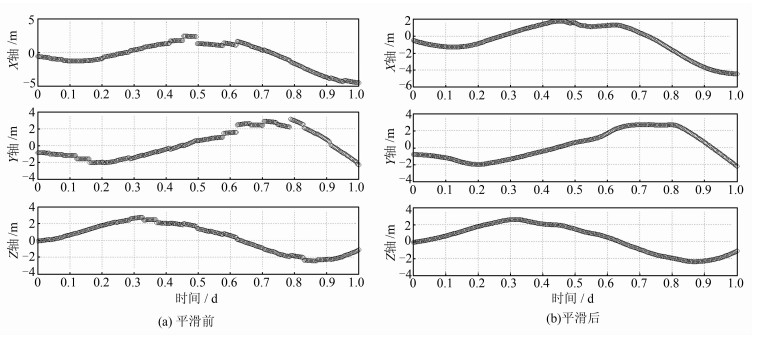
本文采用Robust-Loess数值滤波方法进行轨道预报误差平滑[22]。Loess滤波采用最小二乘拟合方法,即滤波参数p取1,而Robust-Loess滤波增加了稳健估计的思想,该方法对某些野值点的抗差性更好,使得这些野值点不影响整个平滑效果。图 1给出了某IGSO卫星在2012年225 d预报1 d的轨道预报误差及平滑后的预报误差。可以看出,平滑处理后的轨道预报误差连续,可以满足其作为神经网络训练样本的要求。
|
| 图 1 平滑前后的轨道预报误差 Fig. 1 Predictive Orbit Error Before and After Smoothing Filtering |
中期轨道预报弧长为14~27 d,长期轨道预报弧长大于27 d。由动力系统的稳定性概念可知,航天器的受摄运动方程对应一个动力系统,该系统的初值不稳定性使得利用不同初始轨道得到的预报轨道特性会不同。以某初始时刻下的预报误差作为训练样本训练得到的神经网络可以对其他初始时刻下的预报轨道提供补偿,但前提是两个初始时刻的预报误差数值大小及波形图要相近。而由于初值不稳定性导致不同初始时刻的预报误差并无规律。图 2、图 3分别给出了某GEO 2012年225~260天共35 d分别预报15 d和30 d的最大预报误差趋势图。

|
| 图 2 GEO卫星预报15 d的误差最大值统计 Fig. 2 Maximum for GEO in 15 d Prediction |

|
| 图 3 GEO卫星预报30 d的误差最大值统计 Fig. 3 Maximum for GEO in 30-day Prediction |
从图 2、图 3可以看出,GEO卫星的中长期预报误差呈现以14 d为周期的变化规律,实验表明IGSO卫星具有相同的特征。
本文将作为训练样本的预报误差选择定义在直角坐标系中,主要是因为在该坐标系中预报误差的规律性强,便于神经网络的训练,而如果采用RTN坐标系,轨道预报误差最大值也呈现14 d周期的规律,但是T、N方向主要呈线性发散(长期项)的趋势,有的呈线性(长期项)和周期性(周期项)混合的发散趋势,其规律性特点不适合神经网络模型的训练及补偿。
根据上述规律,可以给出中期预报的预报方案为:用当前时刻起14 d之前那天利用动力学模型得到的预报轨道和轨道预报误差作为训练样本,训练得到神经网络模型,采用神经网络模型计算得到的补偿误差波形对当前的预报误差进行补偿,这种方案可使神经网络模型实现轨道的中期预报。长期预报的方案与中期类似,不同的是预报28 d时采用当前时刻起28 d之前那天的预报轨道作为训练样本。
表 1给出了中长期预报方案示意图,预报过程神经网络可提供14 d左右的补偿信息。如要延长补偿时间,则需延长训练样本的时间跨度,方法是以T-28、T-42作为训练的初始时刻:
| 训练阶段 | 预报阶段 | ||||
| 训练样本 | 神经网络逼近函数 | 动力学模型预报星历 | 神经网络输入 | 神经网络输出 | 神经网络模型预报结果 |
| X(T-14n:T)DM | |||||
| V(T-14n:T)DM | ΔX=f(X,V,T) | X(T:T+m)DM | X(T:T+m)DM V(T:T+m)DM |
ΔX(T:T+m)NN |  (T:T+m)NN (T:T+m)NN |
| ΔX(T-14n:T)DM | |||||
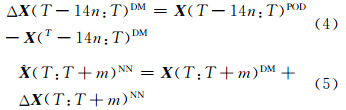
其中,X、V分别为轨道的位置、速度信息;ΔX是轨道的位置误差量;T为某一历元时刻;T-14n(n为正整数)是距离T时刻向前推14n天时的时刻,则训练样本弧段为T-14n到T时刻,预报轨道弧段为T时刻到T+m时刻。各量右上标中,POD表示精密轨道,DM为动力学模型,NN为神经网络模型。
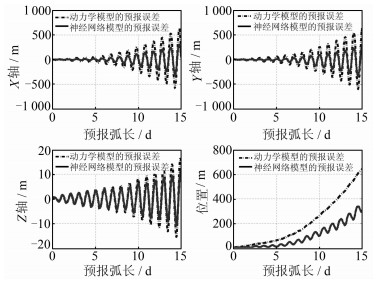
3 实验结果与分析根据预报弧长,分别采用14 d或28 d之前的利用动力学模型得到的预报轨道和轨道预报误差作为训练样本。对于GEO卫星,2012年245 d预报15 d和260 d 预报30 d利用神经网络模型及动力学模型的预报误差分别如图 4、图 5所示,IGSO卫星相应的中长期预报结果如图 6、7所示。
|
| 图 4 GEO卫星中期预报的预报误差图 Fig. 4 GEO’s Predictive Orbit Error Based on Dynamic Model and ANN Model in Medium-Term Prediction |
|
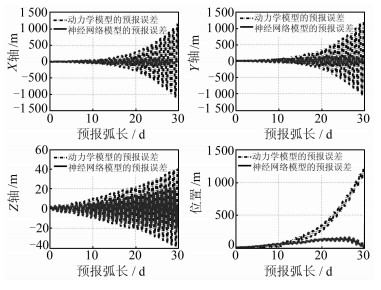
| 图 5 GEO卫星长期预报的预报误差图 Fig. 5 GEO’s Predictive Orbit Error Based on Dynamic Model and ANN Model in Long-Term Prediction |
|
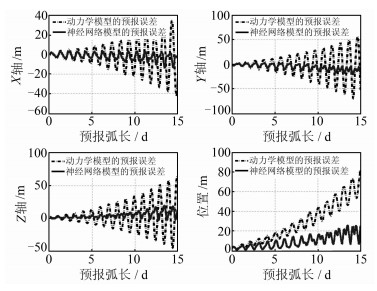
| 图 6 IGSO卫星中期预报的预报误差图 Fig. 6 IGSO’s Predictive Orbit Error Based on Dynamic Model and ANN Model in Medium-Term Prediction |
|
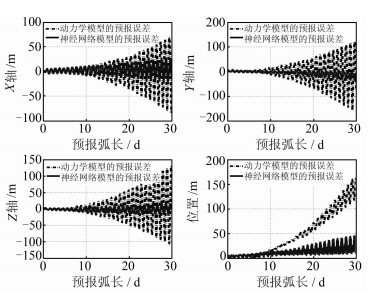
| 图 7 IGSO卫星长期预报的预报误差图 Fig. 7 IGSO’s Predictive Orbit Error Based on Dynamic Model and ANN Model in Long-Term Prediction |
从图 5~8可以看出,以14 d、28 d之前预报结果作为训练样本使神经网络模型实现了在15 d、30 d预报中对误差发散趋势的控制。对于GEO卫星,预报15 d、30 d整体位置预报误差分别由动力学模型的620 m、1 250 m改进到了287 m、290 m。对于IGSO卫星预报15 d、30 d整体位置的轨道预报误差分别由80 m、155 m改进到了21 m、49 m。
采用上述轨道预报方案对其他卫星进行实验分析,其中Sat01为GEO卫星,其余为IGSO卫星。本文中预报误差改进率的计算公式(即改进幅度)为:

其中,Imp_Bit为预报误差的改进率;MaxDyn、MaxNN分别为利用动力学模型和神经网络模型得到的预报误差的最大值。表 2具体给出了各卫星经神经网络模型补偿后的预报精度提高幅度。
| 预报弧长/d | Sat01 | Sat02 | Sat03 | Sat04 |
| 15 | 80.70 | 48.86 | 56.88 | 41.31 |
| 30 | 88.25 | 55.18 | 32.94 | 63.47 |
从表 2中数据可以看出,预报15 d,改进率为41%~80%;预报30 d,改进率为32%~88%。其中,GEO卫星的中长期预报的改进率最高,达80%以上,主要是因为GEO卫星在相同的预报弧长内轨道预报精度差于IGSO卫星,故利用神经网络模型的改进效果更好。由此可知神经网络模型适应于预报误差规律性强的情况,并且此时预报误差越大,其改进效果越好。
4 结 语本文对基于神经网络模型的导航卫星高精度轨道预报技术进行了研究,提出利用神经网络模型进行导航卫星的轨道预报精度补偿,并利用实测数据进行了实验分析,验证了该方法的可行性。
本文给出了利用神经网络模型改进轨道预报精度的思路,将某历史时刻的轨道预报误差作为训练样本,利用训练好的神经网络模型补偿当前的预报轨道以提高轨道预报精度。 神经网络模型对于改进导航卫星的轨道预报精度是有效的,能够为全球卫星导航系统中导航卫星的自主定轨提供长期精密的初轨信息。
| [1] | Abusali P A M, Tapley B D, Schutz B E. Autonomous Navigation of Global Position System Satellites Using Cross-Link Measurements[J]. Journal of Guidance, Control, and Dynamics, System,1998, 21(2): 321-327 |
| [2] | van Helleputte T, Doornbos E. CHAMP and GRACE Accelerometor Calibration by GPS-Based Orbit Determination[J]. Advances in Space Research,2009,43:1 890-1 896 |
| [3] | Jaggi A, Hugentobler U. Precise Orbit Determination for GRACE Using Undifferenced or Doubly Differenced GPS Data[J].Advances in Space Research,2007,39:1 612-1 619 |
| [4] | Visser P N A M, van den Ijssel J. Orbit Determination for the GOCE Satellite[J]. Advances in Space Research,2009,43:760-768 |
| [5] | Montenbruk O, van Helleputte T. Reduced Dynamic Orbit Determination Using GPS Code and Carrier Measurements[J]. Aerospace Science and Technology, 2005,9: 261-271 |
| [6] | Rutkowska M. The Accuracy of Orbit Estimation for the Low-Orbit Satellites LARETS and WESTPAC[J]. Advances in Space Research, 2005,36:498-503 |
| [7] | Sibthorpe A, Bertiger W, Desai S D, et al. A Performance Evaluation of GPS Satellite Solar Radiation Pressure Strategies[C]. IGS Workshop,Newcastle, England, 2010 |
| [8] | Rodriguez-Solano C J, Hugentobler U, Steigenberger P. Precise GNSS Orbit Determination Using an AdjusTablele Box-Wing Model for Solar Radiation Pressure[C]. IUGG Melboume, Melbourne, Australia, 2011 |
| [9] | Gobinddass M L, Willis M. Improving DORIS Geocenter Time Series Using a Empirical Rescaling of Solar Radiation Pressure Models[J]. Advances in Space Research,2009,44:1 279-1 287 |
| [10] | Chen Junping. The Model of Solar Radiation Pressure in Orbit Determination for GPS Satellites[J]. Astronomy Transaction, 2006,47(3):310-319 (陈俊平.GPS定轨中的太阳辐射压模型[J].天文学报,2006,47(3):310-319) |
| [11] | Springer T A,Beutler G, Rothacher M. New Solar Radiation Pressure Model for GPS Satellites[J].GPS Solutions, 1999, 2(3): 50-62 |
| [12] | Lin Xueyuan, Ju Jianbo. Neural Network Prediction Research of GPS/SINS Integrated Navigation System[J]. Geomatics and Information Science of Wuhan University, 2011,36(5):601-604 (林雪原,鞠建波.利用神经网络预测的GPS/SINS组合导航系统算法研究[J]. 武汉大学学报·信息科学版,2011,36(5):601-604) |
| [13] | Nie Jianliang, Gao Weiguang, Zhang Shuangcheng. Dynamic Precise Point Positioning Algorithm of Fault Diagnosis Based on BP Neural Network[J]. Geomatics and Information Science of Wuhan University, 2010,35 (3):283-285(聂建亮,高为广,张双成.利用BP神经网络的动态精密单点定位故障诊断算法[J]. 武汉大学学报·信息科学版,2010,35 (3):283-285) |
| [14] | Liu Tianlei. Estimation of Orbit and Ephemeris for GPS Satellite Based on Application Neural Network and Polynomial Curve Fitting[D]. Taibei:Taiwan Science and Technology University, 2007(刘添雷.应用类神经网路与多项式曲线拟合估测GPS卫星轨道与星历[D].台北:台湾科技大学,2007) |
| [15] | Zhou Jianhua. A New Method of Middle-Term and Long-Term Orbit Prediction for Navigation Satellite[J]. Surveying and Mapping Transaction, 2011,40 (5): 39-45(周建华.一种导航卫星中长期轨道预报方法[J].测绘学报,2011,40(5): 39-45) |
| [16] | Hagan M, Menhaj M. Training Multilayer Networks with the Marquardt Algorithm[J]. IEEE Transactionson Neural Networks, 1994,5(6): 989-993 |
| [17] | Holmstrom L, Koistinen P. Using Additive Noise in Back-Propagation Training[J]. IEEE Transactions on Neural Networks,1992,3(1):24-38 |
| [18] | Grandvalet Y, Canu S. Comments on "Noise Injection into Inputs in Back Propagation Learing"[J]. IEEE Transactions on Systems, Man and Cybernetics, 1995, 25(4):678-681 |
| [19] | Ishikawa M. Structural Learning with Forgetting[J]. Neural Network, 1996, 9(3): 509-521 |
| [20] | Mackay D J C. Bayesian Interpolation[J].Neural Computation, 1992, 4: 415-447 |
| [21] | Lampinen J, Vehtari A. Bayesian Approach for Neural Networks-Review and Case Studies[J]. Neural Networks, 2001,14:13-20 |
| [22] | Ludeman L C. Random Processes: Filtering, Estimation and Detection[M]. Beijing: Electronic Industry Publishing House, 2005 |
 2015, Vol. 40
2015, Vol. 40


