
文章信息
- 徐克科, 伍吉仓, 王成
- XU Keke, WU Jicang, WANG Cheng
- 利用GNSS位移时空序列进行断层无震蠕滑特征分析
- Analysis of Fault Aseismic Slip Feature Based on GNSS Displacement Time-Space Series
- 武汉大学学报·信息科学版, 2015, 40(9): 1247-1252
- Geomatics and Information Science of Wuhan University, 2015, 40(9): 1247-1252
- http://dx.doi.org/10.13203/j.whugis20140347
-
文章历史
- 收稿日期: 2014-04-30
2. 河南理工大学测绘与国土信息工程学院, 河南 焦作, 454000
2. School of Surveying and Land Information Engineering, Henan Polytechnic University, Jiaozuo 454000, China
中国地壳运动观测网络在青藏高原、川滇和华北首都圈等地壳运动活跃区和断层地带进行了重点布设,主要用于研究这些区域的地壳形变特征,构建板内块体构造形变模型,尤其在板块运动速度场,应变求取,以及同震、震后等静态反演方面取得众多研究成果[1, 2, 3]。随着连续和区域GNSS网观测的持续积累,形成了分布在监测区域地表上的测站位移时空序列,有力地促进了对地震震源机制和断层破裂过程的研究。目前,在动态时空反演和异常检测等方面取得了许多研究成果[4, 5, 6, 7, 8, 9, 10],然而,反演之前需知道断层的几何参数与滑移特征等先验信息。鉴于断层形变具有高空间相关性的特点,本文利用地表GNSS时空数据,从主成分时空响应分析的角度研究了断层不同滑移类型和演化特征对地表位移造成的时空影响,提出了直接由GNSS时空数据揭示断层滑移特征与演变过程的方法。
1 分析方法首先对地表GNSS站位移时空序列进行预处理,剔除粗差,补齐缺失数据,去除长期趋势项、年/半年周期项、阶跃和共模误差。之后,对剩余的部分采用主成分时空响应分析[11],如对于一个共有m站和观测了n天的GNSS站位移时空序列,组成矩阵设为Xm×n。其中,每一行代表一个给定站点N、E、U方向所有历元的值,每一列表示在一个给定的历元所有站点的某个分量位移值。为保证所有站点位移都是以零为基点,按式(1)对矩阵实施中心化:

式中,i、j表示矩阵的行列号。对中心化后的矩阵X′m×n进行奇异值分解,即求正交矩阵Um×m、Vn×n和由奇异值构成的矩阵Sm×n,可表示为:
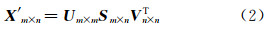
将奇异值按降序排列,对位移时空序列有较大贡献的前几个奇异值称为主模式分量。若取前r个为主模式,则矩阵X则可近似表示为:
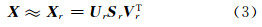
式中,Sr为前r个较大奇异值组成的对角阵;Vr为V中对应前r个列向量组成的矩阵,其中的每一列称为时间特征向量;Ur为U中对应前r个列向量组成的矩阵,其中的每一列称为空间特征向量。主模式数量的确定可以通过卡方统计的方法来确定[6]:
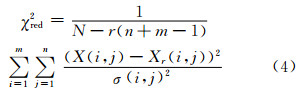
式中,N为总数据个数;N-r(n+m-1)为自由度;σ(i,j)为X(i,j)的中误差。当χred2<1时,表示过度拟合;当χred2>1时,模型与实际数据拟合偏差过大;χred2≈1时,模型拟合效果较好。
主模式时空响应大小是区域性时空变化的主要特征,表示了主分量中各测站各分量位移的相对大小,通过对主成分向量进行归一化处理,可以看出整个时段中,各测站位移的相对大小及同一测站各分量的大小,从而判断断层走向及滑动特征。
2 断层不同蠕滑特征与地表位移关系分析设置断层几何参数见表 1,在断层区域上方的地表按10 km等间隔模拟布设63个GNSS站。由事先设定的断层无震蠕滑滑移类型和演变特征,根据Okada断层位错模型[12],正演地表各站三维位移时空序列。模拟加入不同信噪比的噪声(白噪声和有色噪声)[13],合成较真实的地表位移时空观测序列,利用§1探讨的方法,分析断层不同滑移特征与地表位移序列之间的关系。大量模拟实验结果表明,当地表位移大小至少与噪声水平相当,为有色噪声两倍时,其时空响应分布会出现与实际断层滑移特征较一致的规律,故以下模拟实验设置噪声水平为:白噪声与地表位移大小相当,有色噪声约为地表位移大小的一半。
| 下边缘中心位置(N,E)/km | 方位角/(°) | 长/km | 宽/km | 下边缘深/km | 倾角/(°) |
| (50,50) | 90 | 50 | 10 | 10 | 70 |
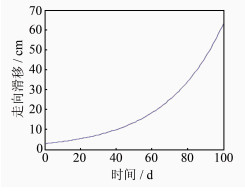
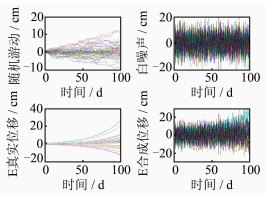
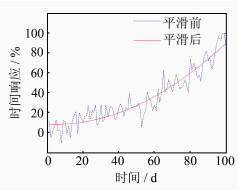
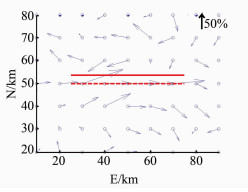
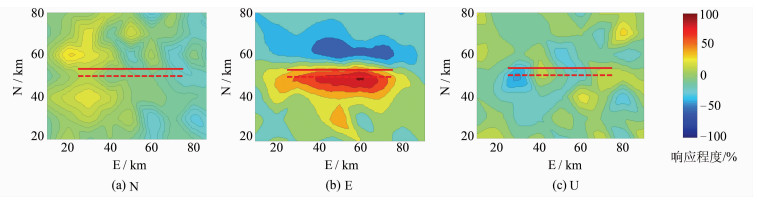
设置100 d的断层走向滑移时间序列,滑移量呈指数函数变化(见图 1)。结合表 1断层几何参数,正演63站地表N、E、U位移时间序列,并模拟加入噪声,合成的E向地表位移时间序列见图 2。对位移时空序列进行主成分时空响应分析,第一主成分时间响应和水平空间响应结果分别见图 3和图 4,N、E、U向位移空间响应场见图 5。图 3~图 5中,实线和虚线表示断层的上、下边缘。由图 3可知,时间响应曲线同样出现了指数形式递增趋势,与事先设定的断层滑移演变过程一致。由图 4和图 5可知,N向和U向的空间响应程度相对较小,约在-0.3%~0.3%之间,且响应分布无规律;而E向空间响应则相反,响应程度较大,主要集中在±1%附近,且分布具有明显的规律,响应梯度最大之处与断层分布出现了高度一致,由此可判断断层走向为E-W。从E向空间响应图看,断层南北两侧空间响应方向相反,且与断层走向平行,由此可判断断层滑移为走向滑移。显然,通过地表位移主成分时空响应分析可以得出断层走向滑移特征,由时间响应变化率来判断断层走向滑移演化过程,由空间响应梯度、方向、大小来判段断层分布、产状和运动方式。
|
| 图 1 实际走向滑移序列 Fig. 1 Real Strike-Slip Series |
|
| 图 2 模拟噪声与合成地表位移序列 Fig. 2 Simulation Noises and Synthetic Displacement Time Series |
|
| 图 3 地表位移时间响应 Fig. 3 Temporal Response of Surface Displacement |
|
| 图 4 走向滑移地表水平空间响应 Fig. 4 Spacial Response of Surface Horizontal from Strike-Slip |
|
| 图 5 走向滑移N、E、U向位移空间响应场 Fig. 5 The Spacial Response Field of Strike Slip N,E,U Displacement |
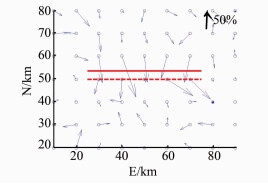
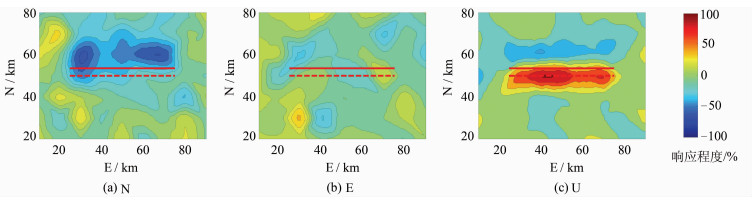
设置100 d的断层逆冲滑移时间序列合成地表位移时空序列,方法同§2.1,进行主成分时空响应分析。第一主成分时间响应同样与事先设置的断层滑移演变曲线相一致。水平空间响应结果见图 6,N、E、U向位移空间响应场见图 7。由图 7可知,E方向空间响应程度相对较小,且分布无明显规律;而N方向和U方向空间响应程度相对较大,且响应程度梯度较大的位置与断层分布出现了较强的一致性,由此根据响应梯度分布判断断层为东西走向。由N向空间响应方向垂直于断层走向,可判断断层为倾向滑移。U向空间响应断层以北为负值,代表下降,断层以南是正值,代表上升,明显是逆冲滑移的结果。综上,均可由时间响应判断断层滑移演变过程,由空间响应梯度判断断层分布,结合U向空间响应方向推断断层的逆冲滑移类型。进行主成分时空响应分析,第一主成分时间响应与事先设置的滑移演变过程一致。水平空间响应序
|
| 图 6 逆冲地表水平空间响应 Fig. 6 Spacial Response of Surface Horizontal from Thrust-Slip |
|
| 图 7 逆冲滑移N、E、U向位移空间响应场 Fig. 7 The Spacial Response Field of Thrust Slip N,E,U Displacement |
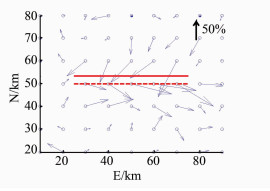
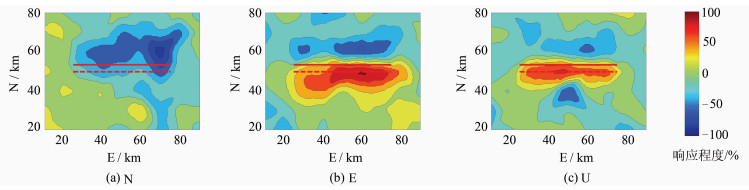
设置100 d的断层走向滑移兼逆冲滑移时间序列,同样正演并加入噪声合成地表位移时空序列,见图 8,N、E、U向位移空间响应场见图 9。由图 9可知,N、E、U向空间响应程度都较大且出现了明显规律,响应程度梯度较大且分布都与断层位置出现了高度一致,由此可判断断层的走向为E-W。由N、E、U向空间响应程度和方向,用§2.1、§2.2节的分析方法,可推断断层滑移类型为走滑兼逆冲滑移。
|
| 图 8 走向滑移兼逆冲地表水平空间响应 Fig. 8 Spacial Response of Surface Horizontal from Strike and Thrust Slip |
|
| 图 9 走向滑移兼逆冲滑移N、E、U向位移空间响应场 Fig. 9 The Spacial Response Field of Strike-Thrust Slip N,E,U Displacement |
由此可见,设置不同的断层滑移类型,通过地表位移主成分时空响应分析均可得到相应的特征。
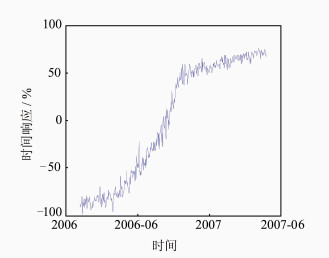
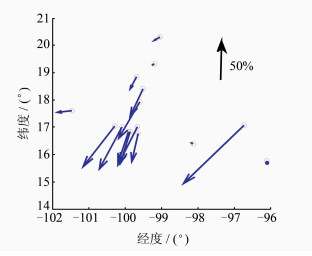
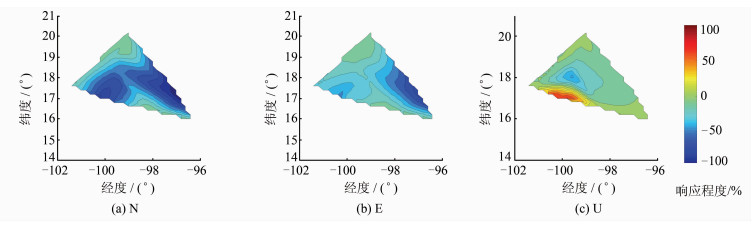
3 实际案例分析墨西哥西南部的格雷罗(Guerrero)州2006年发生了慢滑移事件,这是世界上所观测到的最大的慢地震之一。覆盖断层地表记录有15个GNSS站467 d的位移时间序列[6, 7]。利用本文提出的方法对此位移序列进行了时空分析,第一主成分时间响应和水平空间响应分别见图 10和图 11,N、E、U向位移空间响应场见图 12。由图 10可知,时间响应在2006年3月开始发生明显变化并呈指数函数形式递增。时间响应变化率在2006年7~8月达到了最大,从9月之后开始明显衰减,并逐步趋于稳定。地球物理反演结果表明[7],此次滑移事件是从2006年2月开始,滑移开始发生明显变化,之后滑移速率逐渐增加,在6~7月,滑移速率达到了最大值,为0.5 m/a,之后滑移速率开始逐渐衰退,至2007年1月滑移结束,此时达到了最大滑移量。这与本文通过地表GNSS测站位移时空序列时间响应分析的结果吻合。由图 11、12的空间响应看,最大滑移分布主要集中在两个中心,分别位于(西经100°,北纬17.5°)和(西经98°,北纬17.5°),根据空间响应梯度、方向和模拟实验总结的规律判断,断层走向为WN-ES,断层运动方式以倾滑为主,同时伴有走滑特征。这与有关学者反演所得的断层滑移时空分布结果一致[6, 7]。
|
| 图 10 第一主成分时间响应 Fig. 10 Temporal Response of PC1 |
|
| 图 11 第一主成分空间响应(圆圈代表站点分布) Fig. 11 Spacial Response of PC1 |
|
| 图 12 慢滑移N、E、U向位移空间响应场 Fig. 12 Spacial Response Field of Slow Slip N,E,U Displacement |
鉴于断层滑移引起的地表位移具有强空间相关性的特点,对活动断层地表位移作主成分时空响应分析,能够抓住时空高相关的断层滑移的主要信息,得出了断层滑移类型及演化特征与地表位移主成分时空响应分布密切相关。研究表明,在断层带地表GNSS台站分布合理且数量足够的情况下,根据活动断层带地表位移进行时空响应分析,能够很好地检测出断层破裂过程中的震后余滑和慢地震等无震蠕滑特征与演变过程。 而本文模拟所用的正演模型是基于均匀、弹性、各向同性、半无限空间的有限矩形断层位错理论,还需要进一步考虑地球分层、黏弹性介质等因素的影响,建立更加符合实际的断层位错模型。
在对GNSS站位移时空序列进行主成分分析之前,需要对GNSS数据进行一定的预处理,如剔除粗差、补齐缺失数据、修正阶跃项、消除趋势项、周期项、去除共模误差等。本文方法能够利用覆盖断层的地表GNSS位移时空序列,不需通过反演直接估计断层活动方式,滑移时空分布特征及演变过程,为进行下一步断层参数和滑移特征更为精细的反演提供极其重要的先验信息。因白噪声是时空不相关噪声,对主成分时空响应影响较小,能够适应较低的信噪比,甚至信噪比低于1。随机游动是空间上不相关、时间上相关的噪声,对空间响应分析影响较小,而对时间响应分析敏感。大量实验表明,当信号至少为有色噪声两倍时,时间响应才和实际的断层滑移演变出现较为一致的特征。 因此,在对地表GNSS位移时空序列进行主成分时空响应分析之前,若能构建合理的有色噪声模型,尽量分离有色噪声的影响,将会检测出更加微弱的断层蠕滑时空分布信息。
| [1] | Chen Yongqi, Wu Jicang. Methodology for Monitoring Regional Crustal Deformation Using GPS[J]. Geomatics and Information Science of Wuhan University,2007,32(11):961-966(陈永奇,伍吉仓.利用GNSS监测区域地壳形变的理论与方法[J].武汉大学学报·信息科学版,2007,32(11):961-966) |
| [2] | Wei Wenxin, Jiang Zaisen, Wu Yanqiang, et al. Motion Characteristics of Major Faults in East Boundary of Sichuan-Yunnan Block Obtained with GPS Data[J]. Geomatics and Information Science of Wuhan University, 2012,37(9):1 041-1 044(魏文薪,江在森,武艳强,等.利用GPS数据研究川滇块体东边界主要断裂带运动特性[J].武汉大学学报·信息科学版,2012,37(9):1 041-1 044) |
| [3] | Li Qiang, Jiang Zaisen, Wu Yanqiang, et al. Inversion of Locking and Distribution of Slip Deficit in Haiyuan-Liupan Fault Zone Using GPS Data[J]. Geomatics and Information Science of Wuhan University,2014,39(5):575-580(李强,江在森,武艳强,等.利用GPS资料反演海原-六盘山断裂带闭锁程度与滑动亏损分布[J].武汉大学学报·信息科学版,2014,39(5):575-580) |
| [4] | Segall P, Bürgmann R, Matthews M. Time-Dependent Triggered Afterslip Following the 1989 Loma Prieta Earthquake[J]. Journal of Geophysical Research: Solid Earth, 2000,105(B3): 5 615-5 634 |
| [5] | McGuire J J, Segall P. Imaging of Aseismic Fault Slip Transients Recorded by Dense Geodetic Networks[J]. Geophysical Journal International, 2003, 155(3):778-788 |
| [6] | Kositsky A P, Avouac J P. Inverting Geodetic Time Series with a Principal Component Analysis-Based Inversion Method[J]. Journal of Geophysical Research: Solid Earth, 2010, 115(B3): 401-410 |
| [7] | Radiguet M, Cotton F, Vergnolle M, et al. Spatial and Temporal Evolution of a Long Term Slow Slip Event: The 2006 Guerrero Slow Slip Event[J]. Geophysical Journal International, 2011, 184(2): 816-828 |
| [8] | Ohtani R, McGuire J J, Segall P. Network Strain Filter: A New Tool for Monitoring and Detecting Transient Deformation Signals in GPS Arrays[J]. Journal of Geophysical Research: Solid Earth, 115(B12): 418-428 |
| [9] | Ji K H, Herring T A. A Method for Detecting Transient Signals in GPS Position Time-Series: Smoothing and Principal Component Analysis[J]. Geophysical Journal International, 2013, 193(1): 171-186 |
| [10] | Xu Keke, Wu Jicang, Wu Weiwei. Detection of Transient Aseismic Slip Signals from GNSS Spatio-Temporal Data[J]. Chinese J Geophys, 2015,58(7),DOI:10.6038/Cjg20150701(徐克科,伍吉仓, 吴伟伟. 利用GNSS时空数据检测活动断层瞬态无震蠕滑.地球物理学报,2015, 58(7),DOI:10.6038/Cjg20150701) |
| [11] | Dong D, Fang P, Bock Y, et al. Spatiotemporal Filtering Using Principal Component Analysis and Karhunen-Loeve Expansion Approaches for Regional GPS Network Analysis[J]. Journal of Geophysical Research: Solid Earth, 2006, 111(B3):118-128 |
| [12] | Okada Y.Surface Deformation Due to Shear and Tensile Faults in a Half-Space[J]. Bulletin of the Seismological Society of America, 1985, 75:1 135-1 154 |
| [13] | Agnew D C. Realistic Simulations of Geodetic Network Data: The Fakenet Package[J]. Seismological Research Letters, 2013, 84(3): 426-432 |
 2015, Vol. 40
2015, Vol. 40




