2015, Vol. 40文章信息
- 秦显平, 杨元喜, 崔先强
- QIN Xianping, YANG Yuanxi, CUI Xianqiang
- 椭球参数对北斗与GPS广播星历计算互操作性的影响
- Influence of Ellipsoid Constants on Interoperability of Broadcast Ephemeris Computation Between BeiDou and GPS
- 武汉大学学报·信息科学版, 2015, 40(9): 1237-1241
- Geomatics and Information Science of Wuhan University, 2015, 40(9): 1237-1241
- http://dx.doi.org/10.13203/j.whugis20130475
-
文章历史
- 收稿日期: 2013-09-07
2. 西安测绘研究所, 陕西 西安, 710054;
3. 中南大学地球科学与信息物理学院, 湖南 长沙, 410083
2. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
3. School of Geoscience and Info-Physics, Central South University, Changsha 410083, China
兼容与互操作是多导航卫星系统资源利用与共享的重要内容[1]。然而由于各导航卫星系统由不同国家和地区主导，建设之初对系统兼容与互操作重视不够，加之导航卫星系统庞大、复杂，其时间系统和坐标系统定义各不相同,各系统间的差异给融合应用带来了一些困难。
美国全球定位系统(global positioning system，GPS)采用WGS84坐标系[2, 3]，中国北斗导航卫星系统(简称为BeiDou)采用CGCS2000坐标系[4, 5, 6]。多名学者对我国的坐标系统进行了深入探讨[3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]，比较分析了不同坐标系的定义及影响[12, 13]，并对时空统一下的北斗与GPS融合定位[15]进行了研究。
北斗卫星星座包括地球静止轨道(GEO)卫星、倾斜地球同步轨道(IGSO)卫星及中等高度地球轨道(MEO)卫星[5]。采用广播星历计算卫星位置时，北斗和GPS的广播星历计算都需要用到地心引力常数和地球自转角速度，其中IGSO和MEO卫星与GPS算法相同，GEO卫星与GPS算法仅在轨道倾角旋转方面不同[15, 16, 17]。
文献[12, 13]中,WGS84的地球引力常数和自转角速度与CGCS2000是一致的，广播星历计算时，WGS84与CGCS2000的椭球参数存在微小差异。一方面，这些文献都称为WGS84，容易引起混淆；另一方面，在北斗与GPS的广播星历计算互操作中，对于是否可以忽略这种微小差异，如果不能，这种差异造成的影响有多大的问题，本文从理论和实际数据两方面对这种微小差异的影响进行了比较分析。
1 不同地心引力常数和地球自转角速度常数的比较表 1给出了GPS及北斗广播星历计算时所采用的地心引力常数和地球自转角速度常数[1, 2, 3, 4, 5, 6]。导航卫星所播发的广播星历通常都是由地面控制系统提供的，地面控制系统首先通过卫星定轨得到卫星轨道及预报轨道，然后通过对预报轨道进行参数拟合得到广播星历参数。因此，接收机在利用广播星历进行导航定位时，需要采用与广播星历参数拟合时相同的地心引力常数和地球自转角速度，否则就可能造成错误。
| 地心引力常数GM/(m 3\5s -2) | 地球自转角速度 ω ⊕/(rad\5s -1) | |
| GPS | 3.986 005×10 14 | 7.292 115 146 7×10 -5 |
| 北斗 | 3.986 004 418×10 14 | 7.292 115 0×10 -5 |
北斗地面控制系统在广播星历参数拟合时，采用CGCS2000的地心引力常数和地球自转角速度。GPS早期的地心引力常数取值为3.986 005×10-14，1994年，GPS地面控制系统采用3.986 004 418×10-14计算卫星轨道，地心引力常数的这一改变消除了地面控制系统轨道1.2 m的径向偏差。但是，为了避免GPS接收机软件更新，同时又为了能够提高GPS定轨精度，GPS地面控制系统在定轨时采用3.986 004 418×10-14，而在广播星历参数拟合时仍采用原值3.986 005×10-14。
WGS84定义的地球自转角速度与IERS推荐值相同，为7.292 115 0×10-5 rad/s。该值采用一个常数表示地球自转角速度，事实上地球自转角速度是随时间变化的，考虑到岁差的影响，国际天文学联合会在新的世界时定义中采用7.292 115 146 7×10-5作为地球自转角速度常值。为了与卫星应用保持一致性，GPS地面控制系统采用7.292 115 146 7×10-5进行广播星历参数拟合。
2 地心引力常数对广播星历计算的影响利用GPS广播星历计算卫星位置时，地心引力常数对卫星位置的影响可以采用位置矢量对地心引力常数的微分公式估计，略去繁杂推导，直接给出微分公式为:
=
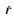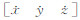T为导航卫星速度矢量;GM为地球引力常数;toe为广播星历参考历元时刻;tk为从参考历元开始计算的观测时间，tk=t－toe。在本文的计算中，地心引力常数差值取为:
dGM=3.986 005×1014-3.986 004 418×1014=5.82×106 由式(1)可知，不同地心引力常数GM对GPS卫星位置影响不仅与卫星的位置和速度相关，还与地球自转角速度和观测时间tk相关。为了验证上述影响公式的正确性，本文首先采用2005-12-10 GPS广播星历计算了不同GM值的位置差(计算位置差)，然后采用式(1)计算了不同GM值的位置差(理论位置差)，并对两种位置差进行了比较。图 1给出了计算位置差与理论位置差之差，其横轴为卫星号，纵轴为计算位置差与理论位置差之差。从图 1可以看出，采用式(1)计算的位置差与实际数据计算的位置差之差仅在10-5 m量级，表明由式(1)表示的地心引力常数误差影响函数正确合理。
|
| 图 1 不同地心引力常数的计算位置差与理论位置差之差 Fig. 1 Comparison of Position Change Between Computation and Theory on Account of the Difference of the Earth’s Gravitational Constant |
图 2给出了2005年12月4日到10日(GPS1352周0~604 800 s)GPS03星计算的卫星位置差，其横轴为时间，单位为GPS周秒，纵轴为表 1中两种不同GM值计算的卫星位置差。图 3给出了所有GPS卫星计算的位置差，其横轴为卫星号，纵轴为不同GM值计算的卫星位置差。从图 2、3可以看出，不同地心引力常数对广播星历计算GPS卫星位置可以引起最大2 m的误差。
|
| 图 2 不同地心引力常数计算的GPS03星位置差 Fig. 2 Difference of Position of GPS03 Satellite Computing by the Difference of the Earth’s Gravitational Constant |
|
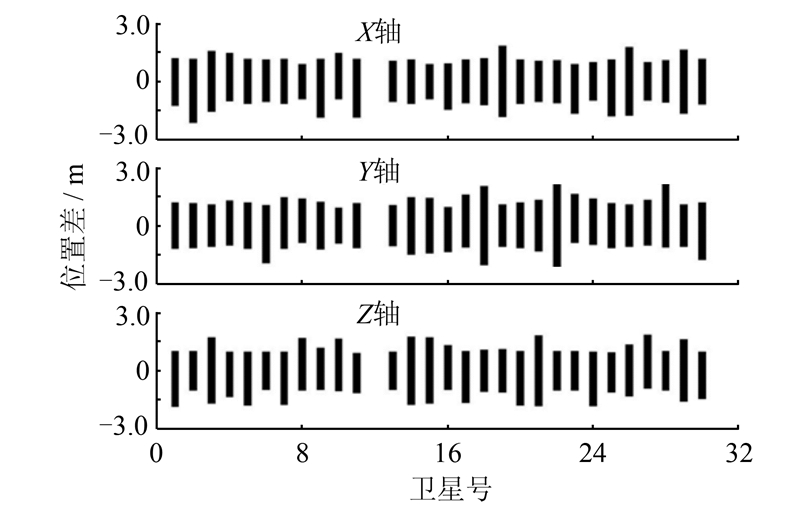
| 图 3 不同地心引力常数计算的GPS卫星位置差 Fig. 3 Difference of Position of all GPS Satellites Computing by the Difference of the Earth's Gravitational Constant |
利用GPS广播星历计算卫星位置时，地心引力常数对卫星位置的影响可以采用位置矢量对地心引力常数的微分公式估计，略去繁杂推导，直接给出微分公式为:
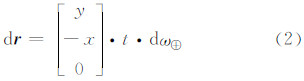
dω⊕=7.292 115 146 7×10-5 -7.292 115×10-5=1.467×10-12
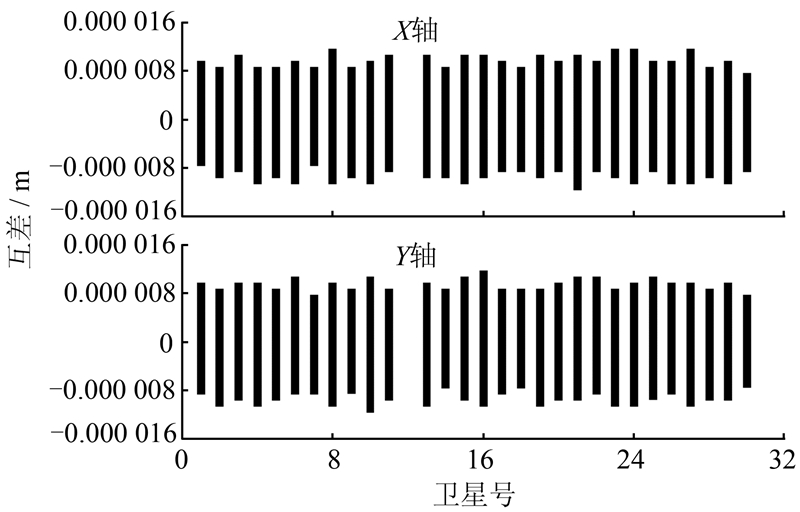
由式(2)可知：(1) 不同地球自转角速度仅对GPS卫星在X轴及Y轴有影响，这种影响不仅与卫星的位置相关，还与观测时间t相关；(2) GPS广播星历是以周秒计时的，这就意味着，在相同条件下，地球自转角速度对每周最后一天的影响最大。同样，为了验证影响式(2)的正确性，本文采用2005年12月10日GPS广播星历计算了不同地球自转角速度的位置差(计算位置差)，然后采用式(2)计算了不同地球自转角速度的位置差(理论位置差)，并对两种位置差进行了比较。图 4给出了计算位置差与理论位置差之差，其横轴为卫星号，纵轴为计算位置差与理论位置差之差。从图 1可以看出，采用式(2)计算的位置差与实际数据计算的位置差之差仅在10-6 m到10-5 m量级，表明由式(2)表示的地球自转角速度影响函数正确。
|
| 图 4 不同地球自转角速度的计算位置差与理论位置差之差 Fig. 4 Comparison of Position Change Between Computation and Theory on Account of the Difference of the Earth's Rotation Rate Constant |
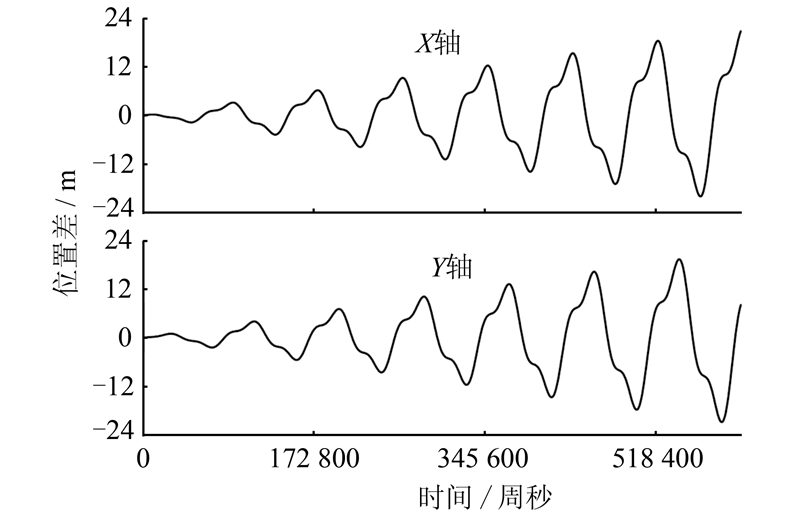
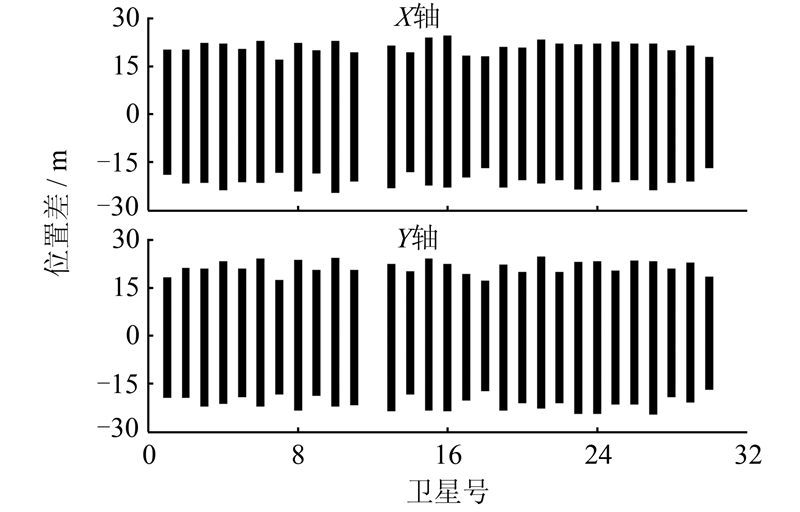
图 5给出了2005年12月4日到10日(GPS1352周0到604 800 s)GPS03星计算的位置差，其横轴为时间，单位为GPS周秒，纵轴为表 1中两种不同地球自转角速度计算的卫星位置差；图 6给出了所有GPS卫星计算的位置差，其横轴为卫星号，纵轴为不同地球自转角速度计算的卫星位置差。由图 5、图 6可以看出，不同地球自转角速度对广播星历计算GPS卫星位置可以引起数十米的误差。
|
| 图 5 不同地球自转角速度计算的GPS03星位置差 Fig. 5 Difference of Position of GPS03 Satellites Computing by the Difference of the Earth's Rotation Rate Constant |
|
| 图 6 不同地球自转角速度计算的GPS卫星位置差 Fig. 6 Difference of Position of all GPS Satellites Computing by the Difference of the Earth's Rotation Rate Constant |
在广播星历计算中，北斗与GPS系统间的地心引力常数差异可以造成卫星位置几米误差，而两者的地球自转角速度差异可以造成十几米甚至几十米的位置误差。因此，在北斗与GPS的广播星历计算互操作中，必须考虑两者之间的地心引力常数和地球自转角速度差异。
| [1] | Yang Yuanxi. Progress, Contribution and Challenges of Compass/BeiDou Satellite Navigation System[J]. Acta Geodaetica et Cartographica Sinica, 2010, 39(1):1-6(杨元喜.北斗卫星导航系统的进展、贡献与挑战[J].测绘学报, 2010, 39(1):1-6) |
| [2] | Xu Qifeng. Space Geodesy:Satellite Navigation and Precise Positioning[M]. Beijing: PLA Publications Inc, 2001(许其凤. 空间大地测量学: 卫星导航与精密定位[M]. 北京: 解放军出版社, 2001) |
| [3] | Zhou Zhongmo, Yi Jiejun, Zhou Qi. The Theory and Application of GPS Satellite Measurement[M]. Beijing: Surveying and Mapping Press, 2002(周忠谟, 易杰军, 周琪.GPS卫星测量原理与应用[M].北京:测绘出版社, 2002) |
| [4] | Tan Shusen. Satellite Navigation and Positioning Project[M]. Beijing: National Defence Industry Publications Inc, 2007(谭述森.卫星导航定位工程[M].北京:国防工业出版社, 2007) |
| [5] | China Satellite Navigation Office. Interface Control Document Concerning BeiDou System Signal-in-Space of (Test Version)[EB/OL]. http://www.beidou.gov.cn/attach/2011/12/27/20111227ace155f4e69a4666b45235e129463872.pdf2011(中国卫星导航系统管理办公室.北斗卫星导航系统空间信号接口控制文件(测试版)[EB/OL].http://www.beidou.gov.cn/attach/2011/12/27/20111227ace155f4e69a4666b45235e129463872.pdf2011) |
| [6] | Yang Y. Chinese Geodetic Coordinate System 2000[J]. Chinese Science Bulletin, 2009, 54: 2 714-2 721 |
| [7] | Chen Junyong. On the Establishment of Chinese Modern Geodetic Coordinate System[J]. Geomatics and Information Science of Wuhan University, 2002, 27(5):441-444(陈俊勇. 我国建立现代大地基准的思考[J]. 武汉大学学报·信息科学版, 2002, 27(5):441-444) |
| [8] | Chen Junyong. Chinese Modern Geodetic Datum: Chinese Geodetic Coordinate System 2000 (CGCS 2000) and its Frame[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 269-271(陈俊勇.中国现代大地基准: 中国大地坐标系统2000(CGCS2000)及其框架[J]. 测绘学报, 2008, 37(3): 269-271) |
| [9] | Wei Ziqing. National Geodetic Coordinate System to Next Generation[J]. Geomatics and Information Science of Wuhan University, 2003, 28(2): 138-143(魏子卿. 我国大地坐标系的换代问题[J]. 武汉大学学报·信息科学版, 2003, 28(2): 138-143) |
| [10] | Wei Ziqing. Re-approaching the Geodetic Coordinate System[J]. Geomatics and Information Science of Wuhan University, 2011, 36(8): 883-886(魏子卿. 大地坐标系新探[J]. 武汉大学学报·信息科学版, 2011, 36(8): 883-886) |
| [11] | Wei Ziqing. Proposal Concerning China Geodetic Coordinate System 2000[J]. Journal of Geodesy and Geodynamics, 2006, 26(2):1-4(魏子卿.关于2000中国大地坐标系的建议[J]. 大地测量与地球动力学, 2006, 26(2):1-4) |
| [12] | Wei Ziqing. China Geodetic Coordinate System 2000 and its Comparison with WGS84[J]. Journal of Geodesy and Geodynamics, 2008, 28(5):1-5(魏子卿.2000中国大地坐标系及其与WGS84的比较[J].大地测量与地球动力学, 2008, 28(5):1-5) |
| [13] | Cheng Pengfei, Wen Hanjiang, Cheng Yingyan, et al. Parameters of the CGCS2000 Ellipsoid and Comparisons with GRS80 and WGS84[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(3): 189-194(程鹏飞, 文汉江, 成英燕, 等. 2000国家大地坐标系椭球参数与GRS80和WGS84的比较[J].测绘学报, 2009, 38(3):189-194) |
| [14] | Ning Jinsheng. Modern Geodetic Reference System[J]. Acta Geodaetica et Cartographica Sinica, 2002, 31(S): 7-11(宁津生.现代大地测量参考系统[J]. 测绘学报, 2002, 31(增刊):7-11) |
| [15] | Gao Xingwei, Guo Jingjun, Cheng Pengfei, et al. Fusion Positioning of Compass/GPS Based on Spatio Temporal System Unification[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(5):743-758(高星伟, 过静珺, 陈鹏飞, 等. 基于时空系统统一的北斗与GPS融合定位[J].测绘学报, 2012, 41(5):743-758) |
| [16] | Cui Xianqiang, Jiao Wenhai, Qin Xianping. The Discussion of Fitting Algorithm of GPS Ephemeris Parameters[J]. Science of Surveying and Mapping, 2006, 31(1): 25-26 (崔先强, 焦文海, 秦显平.GPS广播星历参数拟合算法的探讨[J]. 测绘科学, 2006, 31(1): 25-26) |
| [17] | Cui Xianqiang, Jiao Wenhai, Qin Xianping. Ephemeris Parameters of Navigation Satellite and Their Fitting Arithmetic[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2006, 23(1): 23-25(崔先强, 焦文海, 秦显平. 导航卫星的历书参数及其拟合算法[J].测绘科学技术学报, 2006, 23(1): 23-25) |