文章信息
- 王甫红, 龚学文, 刘万科
- WANG Fuhong, GONG Xuewen, LIU Wanke
- 顾及广播星历误差分离吸收的分米级星载GPS实时定轨新方法
- A Novel Decimeter-Level Real-Time Orbit Determination Algorithm Using Space-Borne GPS Measurements with Separation and Absorption of Broadcast Ephemeris Error
- 武汉大学学报·信息科学版, 2015, 40(9): 1230-1236
- Geomatics and Information Science of Wuhan University, 2015, 40(9): 1230-1236
- http://dx.doi.org/10.13203/j.whugis20130682
-
文章历史
- 收稿日期: 2013-11-15
2. 地球空间信息技术协同创新中心, 湖北 武汉, 430079
2. Collaborative Innovation Center for Geospatial Technology, Wuhan 430079, China
近年来,借助全球性、多观测数据以及低成本的星载GPS测量,在轨实时处理星载GPS观测数据及获取卫星高精度的轨道参数,已成为低轨卫星实现轨道测控、对地观测等诸多任务的主要技术手段之一[1, 2]。
受实时性与自主性需求的限制,传统的星载GPS实时定轨方法只能以GPS卫星实时播发的广播星历作为定位基准,并且通常也只以伪距作为主要观测值[1, 2]。GPS广播星历虽然成功实施了精度改进计划,但目前星历轨道与卫星钟的整体误差仍然可达2 m[3];同时,星载GPS伪距观测值的测量噪声通常为0.5~1.5 m左右[4]。因此,虽然定轨可以充分利用低轨卫星轨道的动力学信息,但传统的伪距实时定轨方法的位置精度仍然只能达到1.0 m左右,速度精度也只能达到1.0 mm/s左右[5, 6, 7, 8, 9, 10, 11]。在卫星测高、重力测量、星载SAR观测以及大气探测等诸多航天遥感科学任务中,随着对地观测空间分辨率与实时性要求的逐步提高[12, 13],卫星平台对轨道参数的实时位置精度需求达到亚米级甚至分米级,对速度精度的需求达到亚毫米级甚至更高。显然,传统的星载GPS伪距实时定轨方法难以满足要求,而更高精度的实时定轨方法成为亟需解决的关键问题。
本文首先分析了广播星历误差的影响及其变化特性,并根据广播星历误差的变化特性提出了一种新的星载GPS实时定轨方法。该方法综合使用伪距及高精度的相位数据,同时在卡尔曼滤波模型中设置相应的参数,对广播星历误差进行参数化分离,实现对广播星历误差的有效吸收,从而获得分米级精度的定轨结果。在此基础上,利用自主研制的分米级实时定轨软件,对不同轨道高度的CHAMP、GRACE-A以及SAC-C卫星的实测数据模拟在轨实时处理,以对新方法进行验证。
1 广播星历误差参数化分离 1.1 广播星历误差影响分析在传统的实时定轨方法中,通常利用伪距作为主要观测值,也只能采用GPS卫星实时播发的广播星历计算GPS卫星的轨道及钟差。令广播星历计算的第j颗GPS卫星的位置与钟差记为Xj,Yj,Zj,cδj,星载接收机的位置与钟差记为X,Y,Z,cδR;如果采用双频伪距,消除电离层延迟,令εPj为无电离层伪距组合Pj的观测噪声,ρj为第j颗GPS卫星到星载接收机的几何距离,即ρj=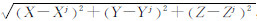 ,则无电离层伪距组合观测方程为:
,则无电离层伪距组合观测方程为:
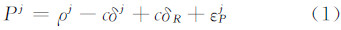
众所周知,广播星历计算的GPS卫星轨道及钟差与真实的卫星轨道与钟差存在一定的差异。将这种差异投影到GPS信号传播路径方向上,本文简称为信号传播路径误差(signal-in-propagation path error,SIPPE)。SIPPE是广播星历的轨道误差与卫星钟误差的综合,直接影响了定位结果。令第j颗GPS卫星真实的位置与钟差为X*,Y*,Z*,cδ*(可以利用IGS事后发布的精密星历计算),第j颗GPS卫星到星载接收机的真实几何距离为ρ*=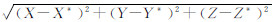 2,则第j颗GPS卫星广播星历的SIPPE的计算公式为:
2,则第j颗GPS卫星广播星历的SIPPE的计算公式为:

结合式(1)与式(2)可以看出,在传统的伪距实时定轨中,并没有顾及GPS广播星历SIPPE的影响,而是将其默认为0,即默认广播星历计算得到的GPS卫星位置与钟差Xj,Yj,Zj,cδj作为定位基准时不存在误差。因此,每个历元进行实时定轨解算时,所有可见GPS卫星的SIPPE的相同部分会被接收机钟差参数cδR吸收,而不同部分(残余部分)则不可避免地进入星载接收机的位置参数X,Y,Z中,这成为限制实时定轨精度提高的关键因素。
1.2 广播星历误差特性分析与参数化分离吸收如前文所述,广播星历的SIPPE是影响实时定轨精度提高的主要因素之一。因此,为实现分米级的实时定轨,必须分析广播星历SIPPE的变化特性,采取相应的处理方法。从式(2)可以看出,SIPPE不仅与GPS卫星广播星历本身的误差有关,而且与星载接收机本身的位置有关。以GRACE-A卫星为例,由于星载接收机无法长时间连续跟踪GPS卫星,图 1给出了2010年第1天一个连续跟踪弧段内PRN02卫星广播星历的径向误差R、沿迹误差T、法向误差N、卫星钟误差CLK以及其在信号传播路径上的综合误差SIPPE,可以看出:①在一个连续跟踪弧段内,GPS 卫星广播星历轨道误差曲线(R/T/N)变化平缓且光滑,而钟误差曲线(CLK)变化平缓但有小量级的随机变化;②SIPPE误差曲线存在明显的缓变趋势,由于钟误差有小量级的随机变化,SIPPE的变化也存在小的随机变化。
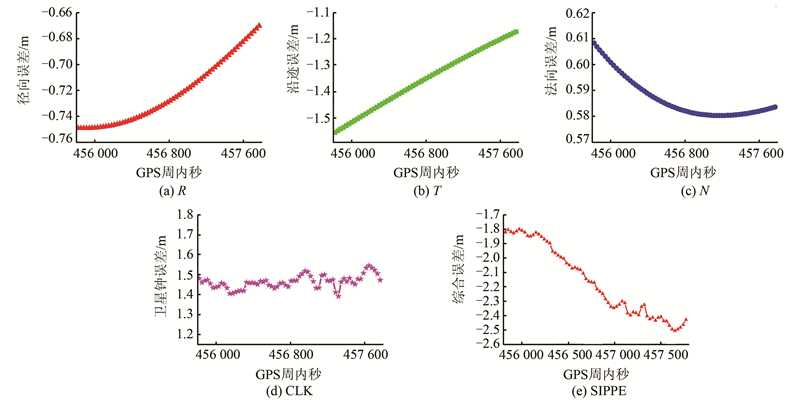
|
| 图 1 GPS卫星广播星历误差 Fig. 1 Errors of GPS Broadcast Ephemeris |
基于上述分析发现的GPS广播星历SIPPE的缓变特性,本文提出直接将广播星历的SIPPE参数化,并同时使用载波相位数据作为主要观测值,从而实现分米级的实时定轨。令第j颗GPS卫星广播星历的SIPPE对应的参数为sippej,采用双频相位观测值,令εjL为无电离层相位组合Lj的观测噪声,Aj为无电离层相位组合的模糊度参数,则观测方程由式(1)变为:
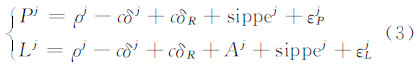
由式(3)可以看出,在实时定轨中,每个历元的所有GPS卫星广播星历SIPPE的相同部分仍然会被接受机钟差参数吸收,残余SIPPE的大部分会被sippe参数吸收,由于模糊度参数无法固定,因此,浮点解得模糊度参数也会吸收小部分的SIPPE。由此也可以预见,由于采取了广播星历误差的参数化分离方法,其误差会被大部分吸收,对应的实时定轨精度也会大幅度提高。
2 分米级实时定轨的数学模型在前文的分析中,针对广播星历误差的缓变特性,本文提出同时使用伪距与相位作为主要观测值,对广播星历误差进行参数化分离吸收,从而实现分米级精度的实时定轨。分米级实时定轨方法的观测方程见式(3),可以看出,模糊度参数与sippe参数成为分米级实时定轨卡尔曼滤波模型中待估的主要参数之一。对于其他待估参数,与传统的伪距实时定轨方法一样,具体可参见文献[6]。因此,分米级实时定轨中,卫星的待估参数状态向量拓展为:
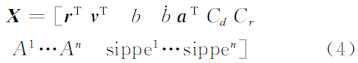
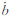 分别为星载接收机的钟差与钟速;a=[aR aT aN]为R、T、N三个方向的补偿加速度;Cd为大气阻力系数;Cr为太阳光压系数;每颗GPS卫星对应一个模糊度参数A与一个误差吸收参数sippe,如果观测到n颗GPS卫星,为13+2n维。相比于传统方法,分米级实时定轨方法的状态向量的维数增加了2n维。
分别为星载接收机的钟差与钟速;a=[aR aT aN]为R、T、N三个方向的补偿加速度;Cd为大气阻力系数;Cr为太阳光压系数;每颗GPS卫星对应一个模糊度参数A与一个误差吸收参数sippe,如果观测到n颗GPS卫星,为13+2n维。相比于传统方法,分米级实时定轨方法的状态向量的维数增加了2n维。
同样,分米级实时定轨的卡尔曼滤波的函数模型也可以表示为:
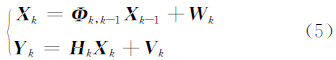
对于sippe参数的随机模型,根据前文所呈现出来的广播星历SIPPE的缓变特性,本文提出使用随机游走过程来模拟其变化特性,用差分方程表示为:
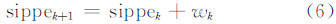
采用自主研制的星载GPS精密自主定轨软件SATPODS进行实验分析,实验数据选用轨道高度分别为320 km、460 km与700 km的CHAMP、GRACE-A与SAC-C卫星连续31 d内的星载GPS实测数据,其中,CHAMP卫星采用2008年年积日(DOY)在200~230内的数据,GRACE-A卫星为2010年DOY为1~31的数据,SAC-C为2008年DOY为38 ~68的数据。所有定轨结果与JPL提供的事后精密星历进行比较,分析其定轨精度。
利用SATPODS软件,设计了4种实验方案,对实测数据进行模拟实时处理,如表 1所示。其中,方案一即是传统的伪距实时定轨方法,方案四是本文重点分析的分米级实时定轨方法,而方案二与方案三作为对照实验用来分析引入相位观测值与广播星历SIPPE参数化对定轨结果的影响。
| 方案 | 特点 | 备注 |
| 方案一 | 伪距观测值+广播星历SIPPE未参数化 | 传统的伪距实时定轨方法 |
| 方案二 | 伪距观测值+广播星历SIPPE参数化 | 作为对照实验 |
| 方案三 | 伪距与相位观测值+广播星历SIPPE未参数化 | 作为对照实验 |
| 方案四 | 伪距与相位观测值+广播星历SIPPE参数化 | 分米级实时 定轨方法 |
由于三种低轨卫星所处高度不同,因此相应配置的重力场模型精度也有所不同。重力场模型都采用EGM2008,SAC-C轨道较高,阶次仅为50×50;GRACE-A卫星次之,阶次为70×70;CHAMP卫星轨道太低,阶次为100×100。对于其他定轨策略,4种方案的设置完全相同,如表 2所示。
| 模型/参数 | 相关设置 |
| 日月 N体引力 | 采用近似公式计算日月位置 |
| 固体潮 | 简易固体潮模型 |
| 大气阻力 | 改进后的Harris-Priester模型,固定表面积,估计 C d参数 |
| 太阳光压 | 简单的球状模型,固定表面积,估计 C r参数 |
| 经验加速度 | 动力学模型补偿(DMC),一阶高斯-马尔可夫随机模型 |
对于方案三与方案四,由于新增加了sippe参数,因此下文详细介绍该参数的相关设置与处理方式。
1) 由于实时定轨中无法获取精密的GPS星历,因此广播星历真实的SIPPE无法计算,所以误差吸收参数sippe的初值通常设置为sippe0=0.0,同时设置较大的初始方差σ02=(5.0 m)2。
2) GPS卫星连续正常跟踪,sippe参数的过程噪声的方差Qk根据广播星历SIPPE的变化率来设置。本文通过大量计算分析发现,对于不同轨道高度(200~1 500 km)的低轨卫星而言,GPS广播星历SIPPE的变化率略有不同,但最大都不会超过3 mm/s。因此,本文将sippe参数的过程噪声方差设置为(3 mm/s·dt)2,其中,dt为滤波中前后历元的时间间隔。
3) 当广播星历出现更新时,则需要重新初始化该颗GPS卫星对应的sippe参数。
4) 如果跟踪锁定新的GPS卫星,则针对该卫星在滤波器中增加相应的sippe参数,并初始化。
5) 如果某颗GPS卫星由可见变为不可见,则直接在滤波器中删除相应的sippe参数。
3.2 实验结果精度分析利用4种方案处理31 d内CHAMP、GRACE-A与SAC-C的星载GPS数据,统计定轨结果的平均位置精度和速度精度(3DRMS),如表 3所示,其中,括号内为切向方向的位置误差RMS与速度误差RMS。比较方案一(传统的伪距实时定轨方法)与方案二可以看出,只采用伪距作为主要观测值,同时增加sippe参数,可以提高定轨精度,但相比于方案四(分米级实时定轨方法),其精度相差15~25 cm左右,其原因在于伪距观测值的观测噪声较大,使得sippe参数对广播星历误差的分离吸收有限。比较方案一与方案三可以看出,相位数据的引入消除了观测噪声的影响,定轨精度得到提高,但由于无法对广播星历SIPPE进一步吸收,因此方案三相比于方案四,定轨精度仍相差15~20 cm左右。比较方案一与方案四可以看出,对于不同轨道高度的低轨卫星,本文提出的分米级实时定轨新方法(方案四)的位置精度达到30~40 cm,速度精度达到0.3~0.5 mm/s,相比于传统方法,精度提高了50%以上。
| 卫星/方案 | 位置/cm | 速度/(mm\5s -1) | |
| CHAMP | 方案一 | 80(58) | 0.88(0.29) |
| 方案二 | 65(49) | 0.62(0.27) | |
| 方案三 | 57(46) | 0.58(0.25) | |
| 方案四 | 40(32) | 0.48(0.22) | |
| GRACE-A | 方案一 | 85(71) | 0.86(0.32) |
| 方案二 | 54(43) | 0.59(0.29) | |
| 方案三 | 51(35) | 0.52(0.24) | |
| 方案四 | 34(27) | 0.37(0.17) | |
| SAC-C | 方案一 | 69(57) | 0.72(0.18) |
| 方案二 | 60(47) | 0.62(0.18) | |
| 方案三 | 55(42) | 0.57(0.17) | |
| 方案四 | 37(32) | 0.38(0.16) | |
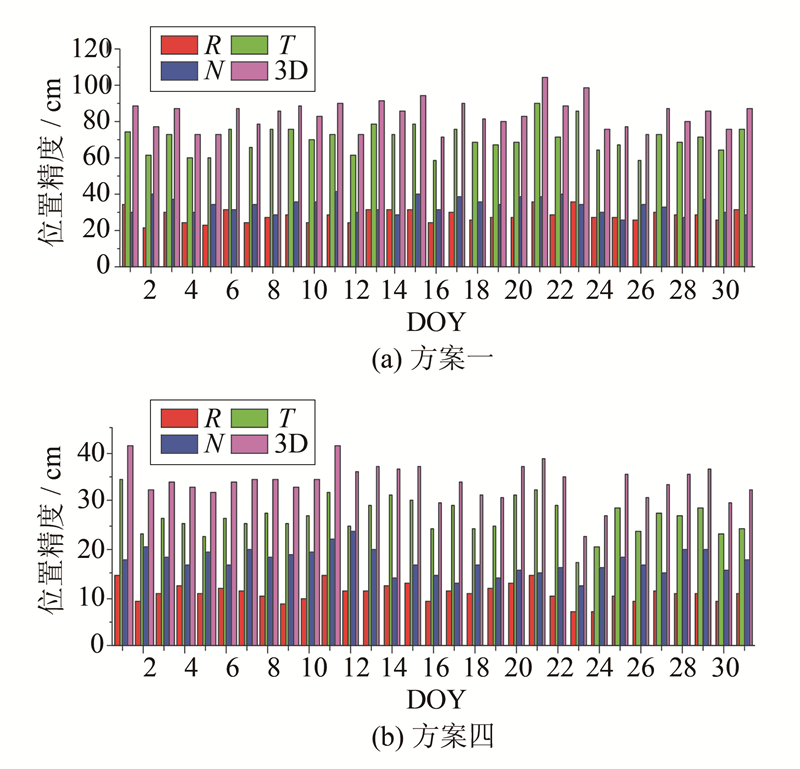
比较每天的定轨精度,图 2统计了2010年DOY为1~31期间GRACE-A卫星采用传统方法与新方法定轨时的位置精度。可以看出,传统伪距实时定轨方法的3D位置精度(RMS)为70~110 cm,切向精度为60~90 cm;而新方法的3D位置精度为20~45 cm,切向精度为15~35 cm,相比于传统方法,精度得到大幅度提高,这与当前国际上最新的实时定轨水平相当[8]。
|
| 图 2 两种定轨方法位置精度比较 Fig. 2 Comparison of Two Real-Time Orbit Determination Methods in Position Accuracy |
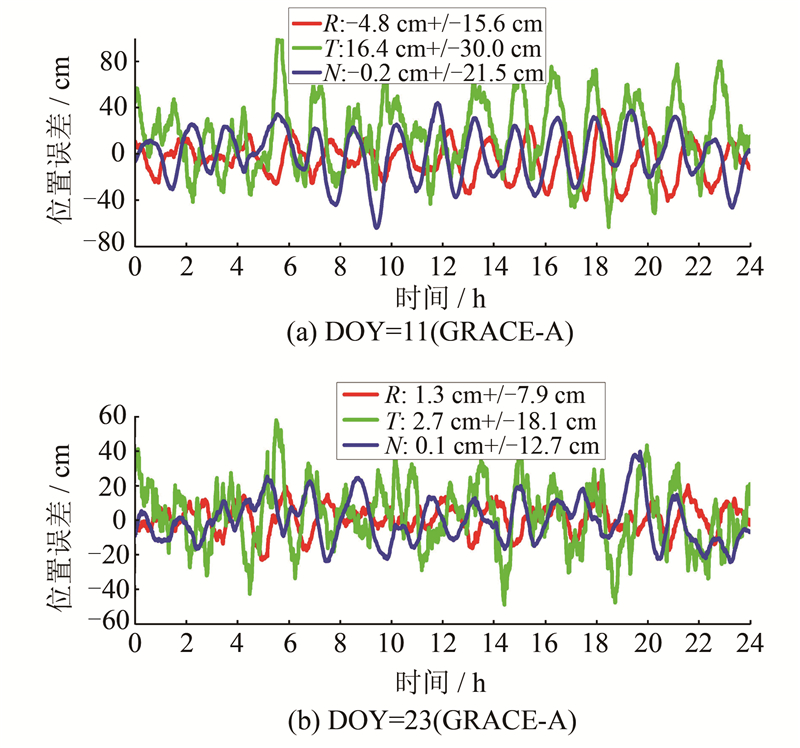
图 3给出了图 2(b)中新方法定轨精度最差(DOY=11,3DRMS=44 cm)与精度最优(DOY=23,3DRMS=23 cm)时的误差曲线,可以看出,前者在R/T/N方向的误差最大不超过±100 cm,后者在R/T/N方向的误差优于±60 cm。
|
| 图 3 分米级实时定轨的位置误差曲线 Fig. 3 Position Error of Decimeter-Level Real-Time Orbit Determination |
分米级实时定轨方法精度之所以明显优于传统的伪距实时定轨方法,关键原因在于:传统的伪距实时定轨方法中广播星历误差无法分离,只能部分被接收机钟差参数吸收;而新方法中设置了sippe参数对广播星历误差进行分离,除了接收机钟差参数吸收外,sippe参数能够吸收残余的SIPPE,而模糊度参数的浮点解也能够吸收小部分的SIPPE。
对于某颗GPS卫星,用吸收之前的SIPPE的RMS值减去残余的SIPPE的RMS值,即为被吸收的SIPPE,被吸收的误差占总的SIPPE的比率,即为该颗GPS卫星广播星历的“误差吸收率”,对所有GPS卫星的误差吸收率求取平均值,即为“平均误差吸收率”。
表 4统计了CHAMP、GRACE-A与SAC-C卫星采用两种方法进行定轨计算时的平均误差吸收率。可以看出,相比传统的伪距实时定轨方法,新方法的平均误差吸收率要高出12%~13%左右。在定轨计算期间,广播星历平均的SIPPE约为1.5~2.5 m,这说明新方法比传统方法平均可以多吸收15~30 cm的SIPPE,而CHAMP、GRACE-A与SAC-C可见GPS卫星的平均PDOP值在1.5~2.5左右,这意味着新方法的定轨精度比传统方法高出30~50 cm左右,这与表 3中的定轨精度结果基本吻合。
| 卫星 | 误差吸收率/% | |
| 传统方法 | 新方法 | |
| CHAMP | 73.8 | 86.9 |
| GRACE-A | 80.4 | 92.3 |
| SAC-C | 76.9 | 87.5 |
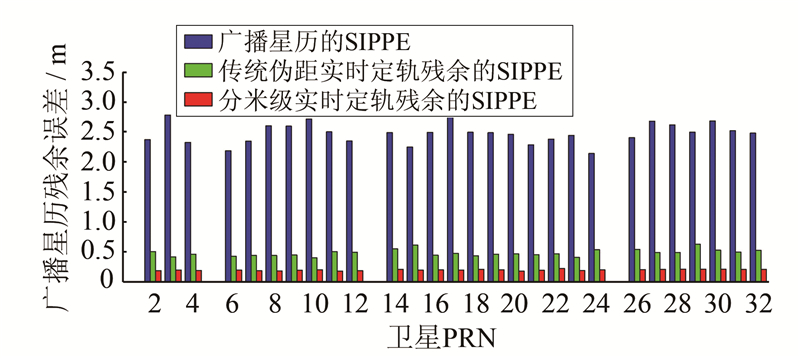
具体分析每颗GPS卫星的广播星历误差吸收情况,图 4给出了GRACE-A卫星定轨计算期间(31 d内)吸收之前每颗卫星广播星历SIPPE的RMS值以及两种定轨方法吸收之后残余的SIPPE的RMS值。可以看出,相比于传统的伪距实时定轨方法,本文提出的新方法吸收的SIPPE更多,残余的SIPPE误差更小。GPS卫星广播星历平均的SIPPE在2~3 m左右,传统的伪距实时定轨方法的平均误差吸收率为80.4%,GPS卫星平均残余的SIPPE约为50 cm。本文提出的分米级实时定轨方法的平均误差吸收率为92.3%,GPS卫星平均残余的SIPPE约为20 cm;而GRACE-A卫星星载接收机可见GPS卫星的PDOP值约为1.5~2.5左右,所以根据残余的SIPPE,可粗略推断传统方法的自主定轨结果精度在75~125 cm左右,而本文提出的新方法定轨结果精度为30~50 cm左右,这与本文给出的定轨结果精度也十分吻合。
|
| 图 4 广播星历残余的SIPPE Fig. 4 Residual SIPPE of Broadcast Ephemeris |
本文提出了一种新的高精度星载GPS实时定轨方法,该方法基于广播星历误差的缓变特性,同时使用伪距与相位作为观测值,通过在卡尔曼滤波模型中设置相应参数对广播星历误差进行分离吸收,从而实现分米级精度的实时定轨。本文模拟实时处理不同轨道高度的低轨卫星的实测数据,对比分析了新方法与传统方法的定轨结果精度与广播星历误差吸收情况,可以得出以下结论。
1) 本文提出的分米级实时定轨方法能够实现30~40 cm的位置精度与0.3~0.5 mm/s的速度精度,相比于传统方法,定轨精度得到大幅度提高,精度可提高50%以上。
2) 本文方法的精度之所以大幅度提高,原因在于新方法中通过对广播星历误差的参数化分离,能够吸收绝大部分的广播星历误差,残余误差大大减小,对于GRACE-A卫星,平均残余误差仅为20 cm左右。
本文提出的实时定轨方法采用对广播星历误差进行参数化分离吸收的方式,在不依赖GPS精密星历或全球差分改正数据的情况下,能够获得分米级的定轨精度。这对于存在高精度实时轨道参数需求的卫星平台有重要的应用价值,但不容避讳的是,新方法的待估参数维数增加,计算复杂度会有一定增加。因此,下一步将重点分析其计算效率及验证其在星载平台上计算的可行性。
| [1] | Goldstein D B. Real-Time, Autonomous Precise Satellite Orbit Determination Using the Global Positioning System[D]. Boulder: University of Colorado, 2000 |
| [2] | Arbinger C, D'Amico S. Impact of Orbit Prediction Accuracy on Low Earth Remote Sensing Flight Dynamics Operations[C]. The 18th International Symposium on Space Flight Dynamics, Munich, Germany, 2004 |
| [3] | Guo Fei, Zhang Xiaohong, Li Xingxing, et al. Precision Analysis on Orbit and Clock of GPS Satellites Broadcast Ephemeris[J]. Geomatics and Information Science of Wuhan University, 2009, 34(5): 589-592(郭斐, 张小红, 李星星, 等. GPS系列卫星广播星历轨道和钟的精度分析[J]. 武汉大学学报·信息科学版, 2009, 34(5): 589-592) |
| [4] | Wang Fuhong, Liu Jiyu. Data Quality Analysis of Space-Borne GPS Code Measurements[J]. Journal of Zhengzhou Institute of Surveying and Mapping, 2007, 24(2): 97-99(王甫红, 刘基余. 星载GPS伪距测量数据质量分析[J]. 测绘科学技术学报, 2007, 24(2): 97-99) |
| [5] | Jia Peizhang, Xiong Yongqing. An Orbit Determination Algorithm with Onboard GPS Using Kalman Filter[J]. Acta Astronomica Sinica, 2005, 46(4): 441-451(贾沛璋, 熊永清. 星载GPS卡尔曼滤波定轨算法[J]. 天文学报, 2005, 46(4): 441-451) |
| [6] | Wang Fuhong. Theory and Software Development on Autonomous Orbit Determination Using Space-Borne GPS Measurements[D]. Wuhan: Wuhan University, 2006(王甫红. 星载GPS自主定轨理论及其软件实现[D]. 武汉: 武汉大学, 2006) |
| [7] | Liu Feng, Ju Tao. Comparison Between Two Onboard Algorithms: Satellite Single-Point Orientation and Satellite Orbit Determination[J]. Journal of Spacecraft TT&C Technology, 2007, 26(4): 25-29(刘涛, 巨涛.单点定位与实时定轨的星载算法的比较研究[J]. 飞行器测控学报, 2007, 26(4): 25-29) |
| [8] | Montenbruck O, Ramos-Bosch P. Precision Real-Time Navigation of LEO Satellites Using Global Positioning System Measurements[J]. GPS Solutions, 2008, 12(3): 187-198 |
| [9] | Florio D S, Gill E, D'Amico S, et al. Performance Comparison of Microprocessors for Space-Based Navigation Applications[C]. The 7th IAA Symposium on Small Satellites for Earth Observation, Berlin, Germany, 2009 |
| [10] | Wang Fuhong. A Kalman Filtering Algorithm for Precision Real-Time Orbit Determination with Space-Borne GPS Measurements[J]. Geomatics and Information Science of Wuhan University, 2010, 35(6): 653-656(王甫红.高精度星载GPS实时定轨卡尔曼滤波模型[J]. 武汉大学学报·信息科学版, 2010, 35(6): 653-656) |
| [11] | Wang Fuhong, Xu Qichao, Gong Xuewen, et al. Application of a Gravity Acceleration Approximation Function in the Precise Real-Time Orbit Determination Using Space-Borne GPS Measurements[J]. Geomatics and Information Science of Wuhan University, 2014, 39(1): 47-51(王甫红, 徐其超, 龚学文, 等. GAAF在星载GPS实时定轨中的应用研究[J]. 武汉大学学报·信息科学版, 2014, 39(1): 47-51) |
| [12] | Li Deren, Shen Xin. On Intelligent Earth Observation System[J]. Science of Surveying and Mapping, 2005, 30(4): 9-11(李德仁, 沈欣. 论智能化对地观测系统[J]. 测绘科学, 2005, 30(4): 9-11) |
| [13] | Li Deren, Tong Qingxi, Li Rongxing, et al. Current Issues in High-Resolution Earth Observation Technology[J]. Sci China Earth Sci, 2012, 42(6): 805-813(李德仁, 童庆禧, 李荣兴, 等. 高分辨率对地观测的若干前沿科学问题[J]. 中国科学:地球科学, 2012, 42(6): 805-813) |
 2015, Vol. 40
2015, Vol. 40



