快速检索        
  武汉大学学报·信息科学版  2015, Vol. 40 Issue (9): 1225-1229

文章信息

安晓亚, 刘平芝, 杨云, 侯溯源
AN Xiaoya, LIU Pingzhi, YANG Yun, HOU Suyuan
一种线状要素几何相似性度量方法及其应用
A Geometric Similarity Measurement Method and Applications to Linear Feature
武汉大学学报·信息科学版, 2015, 40(9): 1225-1229
Geomatics and Information Science of Wuhan University, 2015, 40(9): 1225-1229
http://dx.doi.org/10.13203/j.whugis20130495

文章历史

收稿日期: 2013-09-17
 Abstract              PDF               Figures               Tables
引用本文 0
安晓亚, 刘平芝, 杨云, 侯溯源. 一种线状要素几何相似性度量方法及其应用[J]. 武汉大学学报·信息科学版, 2015, 40(9): 1225-1229.
AN Xiaoya, LIU Pingzhi, YANG Yun, HOU Suyuan. A Geometric Similarity Measurement Method and Applications to Linear Feature[J]. Geomatics and Information Science of Wuhan University, 2015, 40(9): 1225-1229.
一种线状要素几何相似性度量方法及其应用
安晓亚1,2, 刘平芝1,2, 杨云1,2, 侯溯源1,2    
1. 西安测绘研究所, 陕西 西安, 710054;
2. 地理信息工程国家重点实验室, 陕西 西安, 710054
收稿日期: 2013-09-17
基金项目: 国家自然科学基金资助项目(41201469,41071297);地理信息工程国家重点实验室开放基金资助项目(SKLGIE2013-Z-4-1,SKLGIE2013-M-4-5)。
第一作者: 安晓亚,博士,助理研究员,主要从事空间数据相似性及应用方面研究。E-mail:chxyaxy2001@163.com
摘要: 基于传统离散Fréchet距离,提出了一种线状要素几何相似性度量方法。推导了基于递归迭代方法计算离散曲线Fréchet距离的计算公式,因传统Fréchet距离仅用一个点对之间的距离来度量相似性存在较大误差,提出了一种基于离散Fréchet距离识别曲线上点与点之间最短路径的方法,通过最短路径计算两条曲线间平均Fréchet距离,以平均Fréchet距离作为两曲线间的相似值。针对传统Fréchet距离不能解决一条曲线的部分与另一条完整曲线之间的相似匹配,基于平均Fréchet距离,提出了"部分-整体"Fréchet距离计算方法。将上述距离应用于地图数据匹配、合并及等高线内插中,取得了较好的效果。
关键词: 几何相似性     Fréchet距离     数字地图     地图匹配     等高线内插    
A Geometric Similarity Measurement Method and Applications to Linear Feature
AN Xiaoya1,2, LIU Pingzhi1,2, YANG Yun1,2, HOU Suyuan1,2    
1. Xi'an Research Institute of Surveying and Mapping, Xi'an 710054, China;
2. State key Laboratory of Geo-information Engineering, Xi'an 710054, China
First author: AN Xiaoya, PhD, specializes in the spatial data similarity and its applications. E-mail: chxyaxy2001@163.com
Foundation support: The National Natural Science Foundation of China, Nos. 41201469 and 41071297; the Open Research Fund Program of State key Laboratory of Geo-information Engineering, Nos. SKLGIE2013-Z-4-1，SKLGIE2013-M-4-5.
Abstract: Geometric similarity measurement of linear features is the key to matching map data, fusion, and clustering. This paper presents a new method for geometric similarity measurement of digital map linear features based on the traditional discrete Fréchet distance. We derived a formula for computing discrete curves Fréchet distance based on recurrence and presents curves similarity measurement model based on average Fréchet distance. The average Fréchet distance is obtained by recognizing and computing minimal path between points in two curves, which can avoid biggish error of traditional Fréchet distance. Meanwhile, this paper demonstrates that the average Fréchet distance delivers higher accuracy, theoretically. In order to measure the partial and overall similarity between two curves, we also present a partial-overall discrete Fréchet distance based on the average Fréchet distance. Finally, this Fréchet distance was applied to matching map data, fusion and contour interpolation. Experiments were performed to show the feasibility and superiority of the method.
Key words: geometric similarity     Fréchet distance     digital map     map matching     contour interpolation    

线状要素几何相似性度量是多源地图数据网状线要素同名实体几何匹配的关键[1]，其同时可应用于地图导航、空间数据聚类[2, 3]、空间数据渐进式多分辨率传输和制图综合中[4, 5]。文献[6]借助图的方式进行相似性度量，主要适用于度量直角化比较明显的图形，不适用于地图上不规则的线要素。文献[7]提出了线群目标间的方向关系和距离相似性度量模型，该方法易受曲线上局部变形较大点的影响。

对于数字地图而言，曲线间位置的邻近程度更能反应其相似性，一般采用基于距离的方法，主要有Hausdorff和Fréchet距离度量方法，二者的最大差别是前者用来度量离散点集间的距离，而后者用来度量曲线等有序点集间的距离[8]。尽管文献[8]已经提出了计算两条曲线之间离散Fréchet距离的方法，文献[1]也基于该方法研究了不同比例尺地图数据网状要素的匹配，Fréchet距离度量方法存在的问题为：离散Fréchet距离的计算结果是两曲线上两个顶点之间的欧氏距离，当线状要素局部变形很大时，仅用两点之间的距离度量相似性存在较大的误差，度量结果与人的认知存在较大差异；另外，原有的方法还不能解决一条曲线的部分与另一条完整曲线之间的相似匹配(即部分与整体之间的相似性问题)。本文基于传统离散Fréchet距离，提出了平均Fréchet距离和“部分-整体”Fréchet距离以解决上述问题，并将其应用于线状要素匹配、合并以及等高线内插中。

1 离散Fréchet距离的计算方法

给定两参数曲线f:[0, 1]→R2和g:[0, 1]→R2，它们之间的Fréchet距离的定义为[8]：

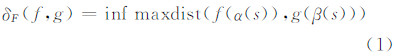
式中，α、β为连续非减的实函数；s为曲线弧长参数；且α(0)=β(0)=0,α(1)=β(1)=1。

线状要素是离散的数字曲线，不能采用式(1)计算两曲线间的Fréchet距离，须在离散化条件下进行计算。设L1、L2分别为离散有序点串： < L1,1,L1,2,…,L1,n>和L2,1,L2,2,…,L2,m>，m、n分别为L1和L2的顶点数，DF为L1、L2之间离散Fréchet距离，可通过式(2)递归求解[8]：

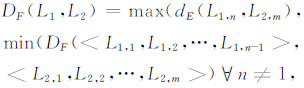
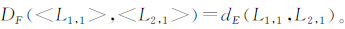
式中，dE(L1,n,L2,m)是点L1,n与L2,m之间的欧氏距离。从( < L1,n>,< L2,m>)开始，利用式(2)递归计算 < L1,1,L1,2,…,L1,n－1>与 < L2,1,L2,2,…,L2,m－1>之间的离散Fréchet距离，最终结果是DF。当线串逐步缩减为一点( < L1,1>,< L2,1>)时递归计算终止，则：

计算离散Fréchet距离过程中有两个矩阵，矩阵维数为n×m。第一个矩阵为M矩阵，矩阵中元素Mij的值是顶点L1，i和L2，j之间的欧氏距离。另一矩阵是K矩阵，矩阵元素Kij=max(dE(L1，i,L2，j), min(K(i－1)j,Ki(j－1),K(i－1)(j－1)))，Knm的值是DF值。

2 离散Fréchet距离的改进 2.1 平均Fréchet距离及顶点间最短路径

平均Fréchet距离Da为两条曲线上点与点之间最短路径的平均值。

约定初始点对(L1，1,L2，1)和(L1，m,L2，n)连接线就是最短路径，然后利用上文所述的两个矩阵M、K和运算符“≤”来计算最短路径，a、b、c、d为实数，若a < c或a==c且b≤d，则有：

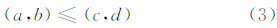
从末点对(L1，m,L2，n)开始，寻找下一个具备“≤”关系的点对。(L1，i,L2，j)下一个可能满足“≤”关系有(L1，(i－1),L2，(j－1))、(L1，(i－1),L2，j)和(L1，i,L2，(j－1))。为确定下一个点对，定义一个二维实数对Ci,j：

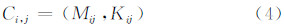
3个候选点对中，如果某一点对对应二维实数对小于或等于其他两个实数对，则该点对即为所求。这一递归求解直到i=1,j=1时结束。

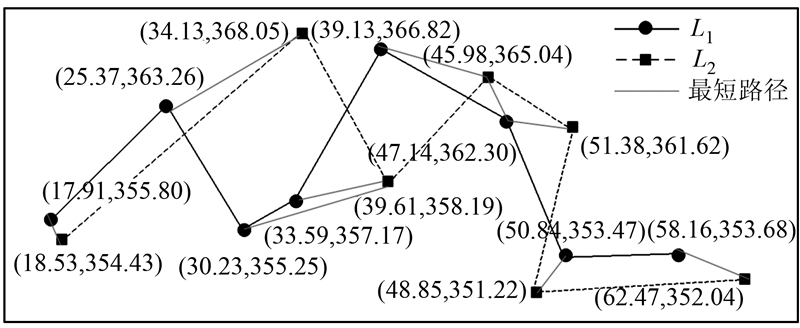
将M和K两个矩阵叠加起来进行求解，表 1中加黑字体即为所求，黑体字行列号就是对应两曲线上的点序号，图 1是将两曲线点集之间最短路径连结之后的效果图。

表 1 求解最短路径的矩阵 Tab. 1 The Matrix of Minimal Path
1 2 3 4 5 6 7 8
1 2.10 2.10 10.81 10.81 11.80 11.80 15.60 15.60 23.92 23.92 30.10 30.10 32.10 32.10 40.76 40.76
2 20.10 20.10 10.21 10.21 12.95 12.95 11.80 10.18 11.80 5.51 14.38 14.38 22.28 22.28 29.02 29.02
3 21.92 21.92 14.94 14.94 10.21 9.68 10.21 5.87 10.21 8.04 10.21 9.05 12.13 12.13 20.21 20.21
4 29.51 29.51 20.71 20.71 18.29 18.29 14.18 14.18 10.21 6.74 10.21 2.80 12.85 12.85 17.58 17.58
5 34.03 34.03 26.02 26.02 21.94 21.94 18.03 18.03 12.90 12.90 10.21 4.05 12.85 8.61 17.58 11.29
6 34.03 31.52 26.16 26.16 21.94 19.13 18.03 16.51 17.78 17.78 11.54 11.54 10.21 2.53 10.69 10.69
7 44.92 44.92 38.61 38.61 32.42 32.42 29.32 29.32 27.14 27.14 18.39 18.39 11.92 11.92 10.21 3.54
表选项
图 1 曲线上点的最短路径 Fig. 1 Minimal Path Between Points in Two Curves
图选项

设两曲线间有N条最短路径Pi(i=1,2,…,N)，则Da为：

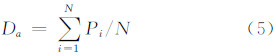
以图 1为例，L1与L2之间的平均Fréchet距离Da为5.16，低于根据式(2)计算出的离散Fréchet距离10.21。

采用平均Fréchet距离代替离散Fréchet距离，是因为前者是从顶点距离集合中选取的一个距离，易受到局部变形较大点的影响，如图 2所示，离散Fréchet距离DF是L1,4与L2,8间的距离，点L2,8局部变形较大，根据上文Da的计算过程，图 2中的小短线即为点之间的最短路径。

图 2 离散Fréchet距离 Fig. 2 Discrete FréChet Distance
图选项

设两曲线间点与点间的距离独立等精度，DF对应相似度精度为mF，Da为ma，设共有P1,P2,…,Pd,…,PN个最短路径，中误差皆为m，设DF=Pd，则有mF=m。由式(5)，根据误差传播律：

当N>1时，有maF，由此证明了平均Fréchet距离代替离散Fréchet距离度量两曲线间的相似性的合理性。图 2中，计算得到DF=6.2 mm，Da=4.3 mm，数字地图上平面位置精度一般为0.2 mm，假定m=0.2 mm，则mF=0.2，ma=0.2/24=0.04 mm。

2.2 “部分-整体”Fréchet距离计算方法

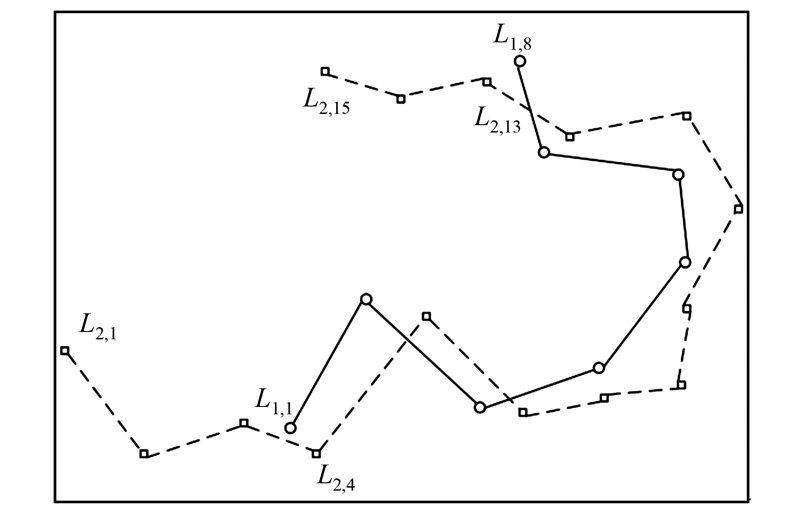
对于诸如图 3所示的同名实体曲线，曲线L2的部分与L1匹配。如果采用前文平均Fréchet距离计算二者的相似度，因为受到L2其他部分端点的影响(在图 3中是(L2,1,…,L2,3)和(L2,14,L2,15))，很难识别出L1与L2部分与整体的匹配关系。为此，基于离散Fréchet距离的计算方法，本文提出了一种“部分-整体”Fréchet距离计算方法，记为Dp。计算Dp的步骤为：

图 3 部分与整体匹配的情况 Fig. 3 Partial and Overall Similarity Matching
图选项

1) 探测到部分匹配曲线的起点和终点(L2,begain,L2,end)(如图 3中的L2,4和L2,13)。遍历L2上所有的点，这些点中选取的起点和终点必须满足起点编号begin < 终点编号end，并且计算出的DF(L1，< L2,begin,…,L2,end >)是最小的。

2) 计算Dp，根据上文，Dp=DF(L1，< L2,begain,…,L2,end >)；

3) 计算平均“部分-整体”Fréchet距离Dap，方法与§2.1相同。

以图 3为例，利用上述步骤计算出“部分-整体”Fréchet距离Dp是1.67，平均距离Dap是0.95。

3 应用与实例 3.1 线要素匹配与合并

根据离散Fréchet距离计算方法及文献[1]线状要素匹配算法，线要素合并的具体流程如下。

1) 根据文献[1]方法完成L1、L2同名曲线匹配。

2) 根据§2.1方法，求解同名曲线上点集最短路径。设整个曲线共有N个最短路径，(L1,i，L2,j)为L1、L2上的第k个路径对应的点对。

3) 采用加权平均方法将连接最短路径的两个点合并为1个点，合并后的点连接成线即为同名曲线合并的结果。点合并过程中若是顶点，则权值较大，反之较小，对于第k个点对(L1,i，L2,j)分别为点对的坐标值，其最终的合并点坐标值Qk(横纵坐标计算公式一样)为：

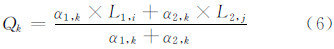
其中，α1,k、α2,k分别为点L1,i、L2,j对应的权值。权值与点所在数据精度和点的位置有关，数据精度越高，权值越大。

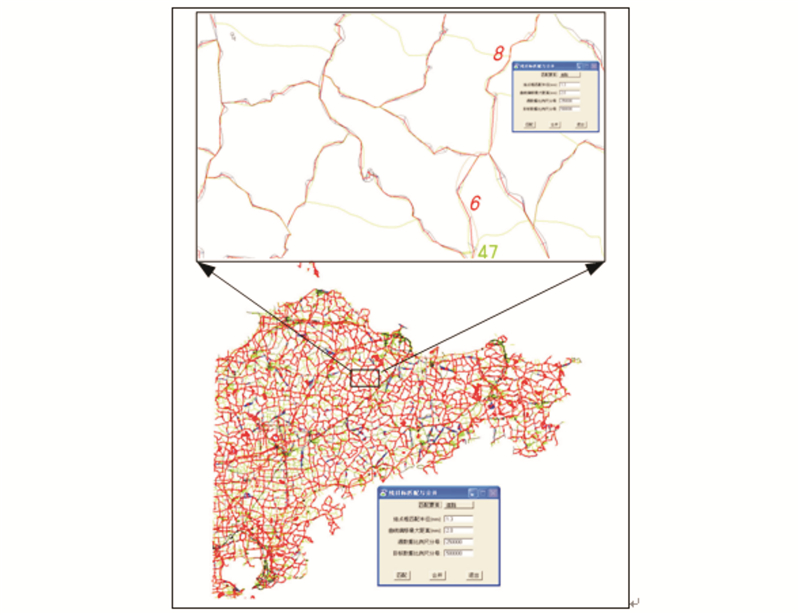
线状要素的匹配合并以道路网为例，所用的数据是华北某区域2005年的1∶25万数字地图数据、2008年的1∶50万数字地图数据。图 4中小短线为同名道路上点之间的最短路径，介于同名道路中间的线为同名道路的合并结果。

图 4 道路网的匹配与合并 Fig. 4 Matching and Combining of Road Network
图选项

将文献[9]算法与本文基于平均Fréchet距离的算法应用于图 4所示的同一区域，设n1为匹配结果中总的实体对数目，r是n1中正确的匹配数目，n2是两种数据源中客观存在的实体对数目，以P=r/n1为查准率，R=r/n2为查全率比较两种算法匹配的效果，具体结果见表 2。

表 2 匹配算法的比较 Tab. 2 Comparison of Matching Algorithm
方法 n 1 n 2 r P/% R/% 速度/(条/s)
文献[9] 2 803 2 921 2 782 99.3 95.2 6.61
本文 2 876 2 921 2 863 99.5 98 7.90
表选项

结果表明，基于本文所提出的曲线相似性度量方法进行道路网数据匹配，其成功率和匹配速度均有较好的表现。

3.2 等高线内插

等高线内插是指在两条等高线间根据距离内插出多根等高线的过程，其实现的关键是构造、划分两条等高线之间的辅助边。利用文献[10]中的基本算法对图 5(a)所示的等高线内插效果不理想，如果采用其改进后的算法，能解决这一问题，但实现起来较为复杂。

图 5 特殊情况等高线内插 Fig. 5 Contour Interpolation in Exceptional Case
图选项

因此，本文利用“部分-整体”Fréchet距离计算方法将两条等高线间局部相似的线段划分出来，然后进行分段内插。根据求两曲线间的最短路径发现，两曲线间的最短路径恰好可以作为辅助边，它能将局部相似的线段划分出来，从而便于等高线内插。以图 5(a)为例，其基本过程为：(1) 依据文献[11]的方法识别形如曲线L1上的弯曲特征点“b”、“c”和“d”点；(2) 根据弯曲特征点将曲线L1划分为“ab”、“bc”、“cd”和“de”4段，分别求每段与曲线L2的“部分-整体”Fréchet距离及曲线上点的最短路径；(3) 以最短路径为辅助边，分段内插等高线，结果如图 5(b)所示。

为验证此方法的有效性，将算法嵌入基于MicroStation的制图系统中，实验数据采用某地区1∶5万地形图数据，在等高线较为稀疏的地区进行内插实验，如图 6所示，粗线是原等高线，细线是内插出的等高线。结果表明，内插出的等高线能够与母线保持形状上相似，反映出该地区的地形起伏特征，不足之处是有些地方会出现等高线相交情况，需要人工编辑。

图 6 基于离散Fréchet距离的等高线内插 Fig. 6 Contour Interpolation Based on Discrete FréChet Distance
图选项
4 结语

针对曲线的相似性度量，本文在传统离散Fréchet距离的基础上，提出了基于最短路径的平均Fréchet距离和“部分-整体”Fréchet距离计算方法，计算结果表明，利用平均Fréchet距离度量曲线相似性能避免线状要素局部变形较大的影响，减少误差，利用“部分-整体”Fréchet距离能解决线要素部分与整体的匹配问题。

参考文献
[1] An Xiaoya, Sun Qun, Yu Bohu. Feature Matching from Network Data at Different Scales Based on Similarity Measure[J]. Geomatics and Information Science of Wuhan University, 2012, 37(2): 224-228(安晓亚, 孙群, 尉伯虎. 利用相似性度量的不同比例尺地图数据网状要素匹配算法[J]. 武汉大学学报·信息科学版, 2012, 37(2): 224-228)
[2] An Xiaoya. Research on Theory, Methods and Applications of Geometry Similarity Measurement for Spatial Data[D]. Zhengzhou: Information Engineering University, 2011(安晓亚. 空间数据几何相似性度量理论方法与应用研究[D]. 郑州:信息工程大学, 2011)
[3] Yang Chuncheng, He Liesong, Xie Peng, et al. Clustering Analysis of Geographical Considering Distance and Shape Area Entities Similarity[J]. Geomatics and Information Science of Wuhan University, 2009, 34(3): 335-338(杨春成, 何列松, 谢鹏, 等. 顾及距离与形状相似性的面状地理实体聚类[J]. 武汉大学学报·息科学版, 2009, 34(3): 335-338)
[4] Tang Luliang, Li Qingquan, Yang Bisheng. Shape Similarity Measuring for Multi-resolution Transmission of Spatial Datasets over the Internet[J]. Acta Geodaetica et Cartographica Sinica, 2009, 38(4):336-340(唐炉亮, 李清泉, 杨必胜.空间数据网络多分辨率传输的几何图形相似性度量[J].测绘学报, 2009, 38(4):336-340)
[5] Qi Huabin. Detection and Generalization of Changes in Settlements for Automated Digital Map Updating[D]. Hong Kong: The Hong Kong Polytechnic University, 2009
[6] Tan Jianrong, Yue Xiaoli, Lu Guodong. Basic Principle, Method of Graphic Similarity and its Application to Structure Pattern Recognition[J]. Chinese J Computers, 2002, 25(9): 959-967(谭建荣, 岳小莉, 陆国栋.图形相似的基本原理、方法及其在结构模式识别中的应用[J].计算机学报, 2002, 25(9):959-967)
[7] Liu Tao, Du Qingyun, Mao Haichen. Spatial Similarity Assessment Model and its Application in Line Groups[J]. Geomatics and Information Science of Wuhan University, 2012, 37(8): 992-995(刘涛, 杜清运, 毛海辰. 空间线群目标相似度计算模型研究[J]. 武汉大学学报·信息科学版, 2012, 37(8): 992-995)
[8] Alt H, Godau M. Computing the Fréchet Distance Between Two Polygonal Curves[J]. International Journal of Computational Geometry & Applications, 1995, 5(1): 75-91
[9] Mustière S, Devogele T. Matching Networks with Different Levels of Detail[J]. International Journal of Geographical Information Science, 2008, 12: 435-453
[10] Hu Weiming, Wu Bing, Ling Haibin. An Automatic Method for Contour Interpolation in Map Design[J]. Chinese J Computers, 2000, 23(8):847-851(胡卫明, 吴兵, 凌海滨.地图等高线自动内插算法[J].计算机学报, 2000, 23(8): 847-851)
[11] Luo Guangxiang, Chen Xiaoyu, Zhao Suoyi. Bend Identification Model of Soft Polygon and the Application[J]. Geomatics and Information Science of Wuhan University, 2006, 31(2):160-163 (罗广祥, 陈晓羽, 赵所毅.软多边形地图要素弯曲识别模型及其应用研究[J]. 武汉大学学报·信息科学版, 2006, 31(2):160-163)