文章信息
- 王洪斌, 赵学胜, 张春亢, 郭俊枫
- WANG Hongbin, ZHAO Xuesheng, ZHANG Chunkang, GUO Junfeng
- 一种基于Morse复形的地形特征线构建改进算法
- An Improved Algorithm of Constructing Terrain Feature Lines Based on Morse Complex
- 武汉大学学报·信息科学版, 2015, 40(9): 1220-1224
- Geomatics and Information Science of Wuhan University, 2015, 40(9): 1220-1224
- http://dx.doi.org/10.13203/j.whugis20130522
-
文章历史
- 收稿日期: 2013-09-23
2. 中国矿业大学(北京), 北京, 100083
2. China University of Mining & Technology(Beijing), Beijing 100083, China
地球表面的形态信息由关键点(极小点、极大点和鞍点)、地形特征线(如山谷线和山脊线)、极值点的影响区域(或均匀梯度场的区域)构成[1]。地表形态模型的构建和表达,能够帮助人们获取地形模型的知识信息,在地形分析和解译、基于知识的推理、水文模拟以及地形综合等领域具有广泛的应用。
关于地表形态特征提取的算法已有很多,如基于规则格网DEM[2, 3, 4, 5]和基于等高线的算法等[6, 7, 8]。此外,以三角格网地形为数据源,人们也提出了许多基于Morse复形的地表形态特征表达算法[9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20]。这些算法中,大多数提取的特征线是按照原始格网顶点寻径,直接通过原始三角形的扩展构建复形单元,具有计算简单、速度较快的优点[9, 10, 11, 12, 15, 16, 17, 18, 19, 20]。然而,得到的特征线往往是“准”梯度线,且由于地形表面复杂多样,常常使山脊线和山谷线在正则点处出现各种各样的“交叉”(见图 1)现象。这不仅违反了其理论基础即Morse理论[21]的基本要求,更重要的是扭曲了极值点与鞍点的连接关系,导致拓扑简化、地形综合等地学应用中主要地形特征的错误取舍。为此,有学者提出了一种避免“交叉”的策略[22],但仅仅解决了单点交叉现象(图 1(a)),而没有涉及多点交叉(图 1(b))、线交叉(图 1(c))及多线交叉(图 1(d))等复杂现象。
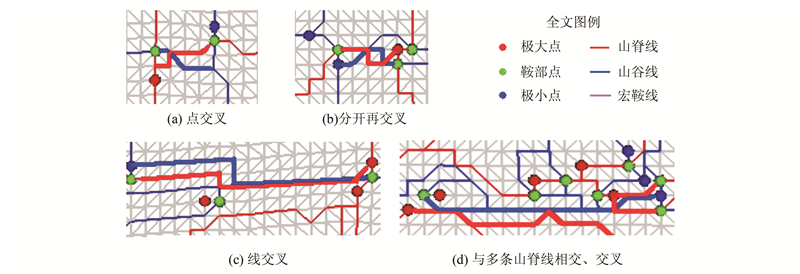
|
| 图 1 传统算法造成的“交叉”形式 Fig. 1 Four Types of Intersections Caused by Traditional Algorithms |
此外,这些算法也很少能够有效识别地表“宏”鞍点,尽管在个别文献中提到了“宏”鞍点的概念[1]。一条特征线途经两个鞍点时,两个鞍点之间的路径既是山脊线一部分又是山谷线一部分,本文称这段路径为宏鞍线。“宏”鞍点的存在,也会造成地表形态拓扑简化和地形综合的不确定性和复杂性[1]。
针对上述问题,本文利用Morse复形的对偶特征,提出了一种较为通用的改进算法。虽然特征线仍从原始格网顶点寻径,但可以完全避免各种“交叉”现象,且能够有效地识别“宏”鞍点,实现整个地形特征线和地表形态的完整构建。
1 Morse理论及Morse复形Morse理论及Morse复形是研究表面形态的有力工具。设f是定义在二维空间(平面)区域D上的二阶可微实函数,对D上任意一点p,若满足p点处的梯度为零,则称p为 f 的关键点(或临界点),否则称为正则点。关键点的类型有极大点、极小点和鞍点三种。如果所有的关键点是非退化的,则函数 f 称为Morse函数。过任意正则点均有一条沿 f 梯度方向的积分线通过。该积分线的起始和终止均为关键点,并且线上各点的切线方向与 f 在该点的梯度方向相同。给定关键点c,定义所有终止于该关键点的积分线集合为c的上升域,称为上升单元;反之,所有起始于该关键点的积分线集合组成c的下降域,称为下降单元。D上所有的下降单元(或上升单元)将区域D剖分成一种欧几里得单元复形,称为下降(或上升)Morse复形。如果两种复形正态相交,则称函数f满足Smale条件,相互叠加构成的新复形称为Morse-Smale复形,相应的分界线构成的网络称为关键网络,如图 2所示。地形分析中,由山谷线和山脊线连接而成的表面网络[23]本质上即为关键网络。
Morse理论的基本前提是函数二阶可微,而实际工程中却很难满足这一要求。为此,人们对经典的Morse理论进行了多种扩展。其中,文献[24]提出的分段线性Morse理论在TIN表示的表面上定义分段线性函数,通过将每个顶点与其相邻顶点的函数值进行比较,实现了关键点的提取及表面形态的表达。其前提假设被弱化为TIN中相邻两顶点的函数值不相等,它更适用于三角格网地形表面的形态表达[25]。然而,如果函数二阶可微,那么对于任一正则点有且仅有一条梯度线经过,梯度线不会出现交叉,但在分段线性函数中该性质并不成立[26]。这是造成上述多种“交叉”的理论根源。
2 改进算法如图 2所示,从两种Morse复形的对偶结构中可以观察到某个上升单元(图 2(c)中青色单元)的边界由山谷线组成,鞍点分布在这些边界线上,连接这些鞍点和该单元极大点的山脊线位于该单元内部。所有上升单元内部的山脊线,构成了下降Morse复形的边界线;类似地,从下降Morse复形的角度看,某个下降单元(图 2(c)中紫色单元)的边界由山脊线组成,连接单元边界鞍点和该单元极小点的山谷线位于该单元内部。所有下降单元内部的山谷线,构成了上升Morse复形的边界。本文算法的主要步骤如下。
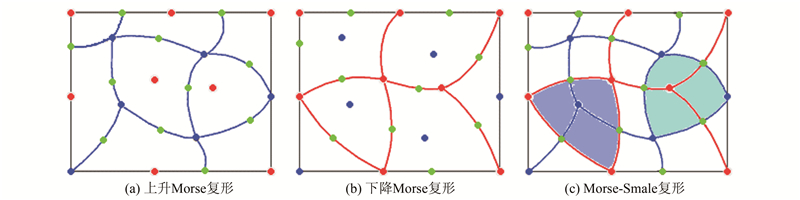
|
| 图 2 Morse和Morse-Smale复形 Fig. 2 Morse and Morse-Smale Complex |
1) 对离散地形点集进行三角剖分,利用现有算法构建下降(上升)Morse复形。
2) 在每个已建单元内,识别单元鞍点,根据鞍点位置按最陡邻点法[10]分类提取对偶复形边界线:(1) 如果鞍点在单元内部,则选取单元内格网顶点直接寻径,终止于单元极值点;(2) 如果鞍点在单元边界上,则根据宏鞍线自身类型的双重性及其路径穿过的鞍点和相邻顶点的关系,判别该鞍点是否是“宏”鞍点。如果是,则严格按照第一步中的既定路径寻径,终止于“宏”鞍点的另一个鞍点;如果不是,则选取单元内合适顶点直接寻径,终止于单元极值点。
3) 利用提取的特征线构建上升(下降)Morse复形,使地表的形态信息得以正确表达。
在上述算法第二步中,由于在已建复形单元内提取对偶复形边界线,保证了特征线寻径选点不会超出整个单元,从而避免了“交叉”的出现。这样,相当于将已有复形单元的边界线作为提取其对偶复形边界线的边缘约束条件。
3 实验与分析本文选取SRTM地形数据,应用C++语言和OSG图形库进行了实验设计与开发。
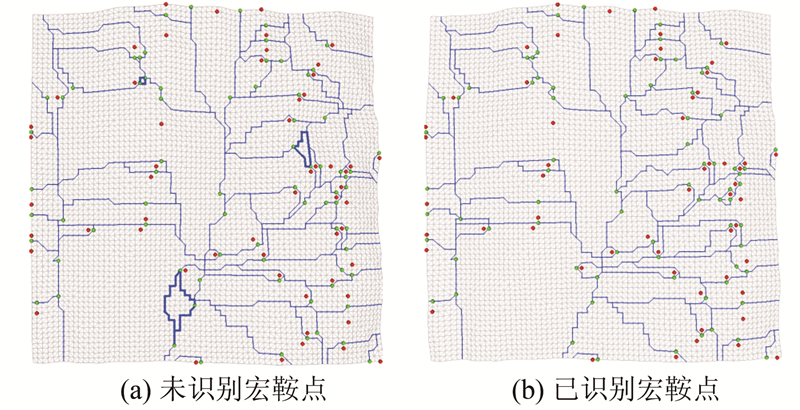
3.1 规则分布的地形高程点集以青藏高原部分地区(90 m分辨率)为实验区域进行了实验,图 3、4分别是利用传统STD算法[15]和本文算法对实验区域构建的地表形态模型及对应区域的局部放大俯视图。图 3局部放大图中“交叉”现象(加粗线条)清晰可见,而图 4的局部放大图则完全避免了“交叉”现象的出现。图 5是利用山谷线构建的上升Morse复形。图 5(a)是传统算法未识别“宏”鞍点的结果,以蓝色加粗线条为边界的区域中没有极大点,区域内所有三角形不属于任何上升单元,即所有上升单元“拼接”起来未能“覆盖”整个地表,不能实现对整个地形的完整划分。图 5(b)是利用本文算法识别“宏”鞍点的结果,可以看出,每个单元边界不重叠,同时内部都有且仅有一个极大点,所有上升单元“拼接”在一起实现了对整个地形的完整剖分。
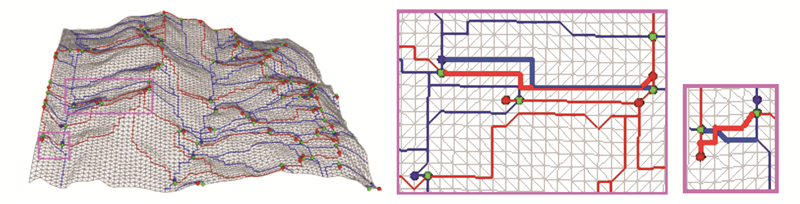
|
| 图 3 传统算法构建的地表形态模型及局部放大俯视图 Fig. 3 Terrain Morphological Model Constructed by the STD Algorithm |
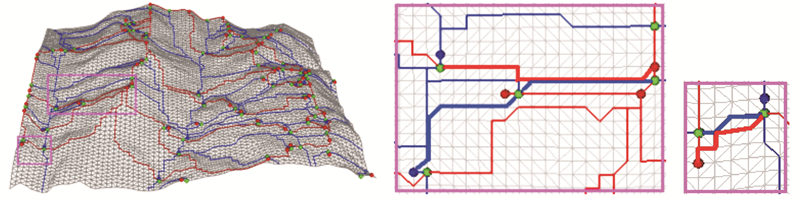
|
| 图 4 本文算法构建的地表形态模型及“交叉”的避免 Fig. 4 Terrain Morphological Model Constructed by the Proposed Algorithm |
|
| 图 5 “宏”鞍点识别前后的上升Morse复形 Fig. 5 Ascending Morse Complex Before and After Identifying the Macro-Saddles |
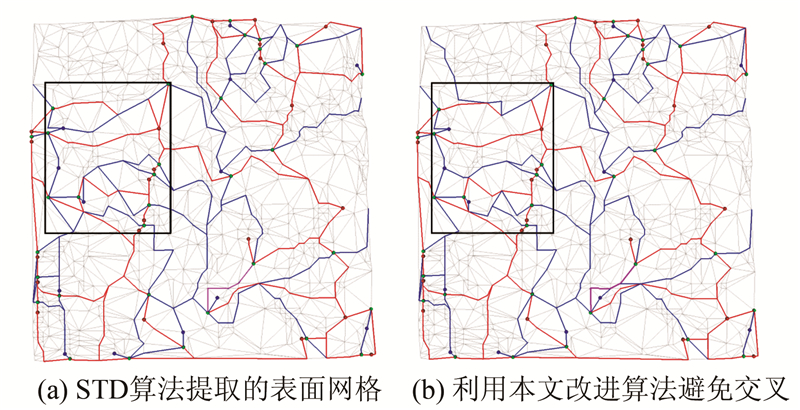
首先,将上述实验区域的地形高程数据集简化为不规则分布的高程点集。然后,对简化数据集生成Delaunay三角网,分别采用STD算法和本文算法构建地表形态模型,结果如图 6所示。可以看出,对于不规则分布的地形高程点集,传统算法同样造成了“交叉”,而本文算法却能够避免这一现象的发生。
|
| 图 6 TIN上的“交叉”及其避免 Fig. 6 Appearance and Prevention of the “Intersection” from TIN |
理论上,基于Morse复形的地表形态表达算法适合于多种尺度的三角格网地形。实际上,利用这类算法对中小尺度的大多数地形进行特征提取和形态表达,其效果更为显著。
4 结语山谷线和山脊线在正则点处交叉及“宏”鞍点的存在,不仅不符合Morse理论的基本要求,而且在拓扑简化、地形综合等地学应用中直接造成主要地形特征的错误取舍。本文利用Morse复形的对偶特征,提出了一种较为通用的改进算法,解决了传统算法存在的上述问题,并开发设计了相关实验,对算法的可行性、适用性进行了验证及分析,主要结论如下:
1) 改进算法得到的特征线点位保留在原始格网点上,通过将下降(或上升)Morse复形的边界作为提取其对偶复形边界的约束线,完全避免了地形表面中出现的各种“交叉”。
2) 算法根据宏鞍线自身类型的双重性及其路径穿过的鞍点和相邻顶点的关系,有效识别出“宏”鞍点,并使多余的特征线合并到“宏”鞍线上,保证了“宏”鞍线的唯一性及地表剖分的完整性。
近年来,高精度点云地形数据的获取已成为现实,基于高精度点云数据的地形特征提取将是本文下一步的研究重点。另外,Morse复形通过“聚类”将数据集划分为独立的子集,这恰好符合并行计算的基本要求,而且本文算法更有利于并行实现。
| [1] | Floriani L D, Magillo P, Vitali M. Modeling and Generalization of Discrete Morse Terrain Decompositions[C]. The 20th International Conference on Pattern Recognition, Turkey, 2010 |
| [2] | Wang Tao. Extraction of Structural Geomorphometrical Information from Digital Elevation Models[D]. Wuhan: Wuhan University, 2009(王涛. 地貌信息提取中的结构化问题研究[D]. 武汉: 武汉大学, 2005) |
| [3] | Tang Guoan, Liu Xuejun, Bian Lu, et al. Landform Skeleton Reconstruction from Unorganized Points[C]. The Second International Conference on Space Information Technology, Wuhan, China, 2007 |
| [4] | Luo Mingliang. Research on Terrain Feature Points Cluster Based on DEM[D]. Chengdu: Institute of Mountain and Environment, Chinese Academy of Sciences, 2008 (罗明良. 基于DEM 的地形特征点簇研究[D]. 成都:中国科学院/水利部成都山地灾害与环境研究所, 2008) |
| [5] | Kong Yueping, Fang Li, Jiang Yonglin, et al. A New Method of Extracting Terrain Feature Lines by Morphology[J]. Geomatics and Information Science of Wuhan University, 2012, 37(8): 996-999 (孔月萍, 方莉, 江永林, 等. 提取地形特征线的形态学新方法[J]. 武汉大学学报·信息科学版, 2012, 37(8): 996-999) |
| [6] | Zhang Yao, Fan Hong, Li Yu'e. A Method of Terrain Feature Extraction Based on Contour[J]. Acta Geodaetica et Cartographica Sinica, 2013, 42(4): 574-580 (张尧, 樊红, 李玉娥. 一种基于等高线的地形特征线提取方法[J]. 测绘学报, 2013, 42(4): 574-580) |
| [7] | Guo Qingsheng, Yang Zuqiao, Feng Ke. Extracting Topographic Characteristic Line from Contours[J]. Geomatics and Information Science of Wuhan University, 2008, 33(3): 253-256(郭庆胜, 杨族桥, 冯科. 基于等高线提取地形特征线的研究[J]. 武汉大学学报·信息科学版, 2008, 33(3): 253-256) |
| [8] | Jin Hailiang, Kang Jianrong, Gao Jingxiang. Research on the Algorithm of Extracting Ridge and Valley Lines Using Contour Data[J]. Geomatics and Information Science of Wuhan University, 2005, 30(9): 809-812 (靳海亮, 康建荣, 高井祥. 利用等高线数据提取山脊(谷)线算法研究[J]. 武汉大学学报·信息科学版, 2005, 30(9): 809-812) |
| [9] | Bajaj C L, Shikore D R. Topology Preserving Data Simplification with Error Bounds[J]. Computers and Graphics, 1998, 22(1):3-12 |
| [10] | Takahashi S, Ikeda T, Kunii T L, et al. Algorithms for Extracting Correct Critical Points and Constructing Topological Graphs from Discrete Geographic Elevation Data[J]. Computer Graphics Forum, 1995, 14(3):181-192 |
| [11] | Qiu Yanjie, Zhou Xionghui, Liu Wei. Feature Lines Extraction from Trianglular Mesh Based on Morse-Smale Complex[J]. Jounal of Shanghai Jiaotong University, 2010, 44(8): 1 074-1 078(邱彦杰, 周熊辉, 柳伟. 基于Morse-Smale复形的三角网格特征线提取[J]. 上海交通大学学报, 2010, 44(8):1 074-1 078) |
| [12] | Edelsbrunner H, Harer J, Zomorodian A. Hierarchical Morse Complexes for Piecewise Linear 2-Manifolds[C]. The 17th ACM Symposium on Computational Geometry, Medford, MA, USA, 2001 |
| [13] | Pascucci V. Topology Diagrams of Scalar Fields in Scientific Visualization[M]. New York: John Wiley and Sons Ltd, 2004 |
| [14] | Bremer P T, Edelsbrunner H, Hamann B, et al. A Multi-resolution Data Structure for Two-Dimensional Morse Functions[C]. IEEE Visualization Conference, Seattle, Washington, 2003 |
| [15] | Magillo E, Floriani L. A Discrete Approach to Compute Terrain Morphology[J]. Computer Vision and Computer Graphics: Theory and Applications, 2009, 21:13-26 |
| [16] | Danovaro E, de Floriani L, Mesmoudi M M. Topological Analysis and Characterization of Discrete Scalar Fields[J]. LNCS, 2003, 2 616: 386-402 |
| [17] | Saux E, Thibaud R, Li K, et al. A New Approach for a Topographic Feature-Based Characterization of Digital Elevation Data[C]. ACM Workshop on Advances in Geographic Information Systems, Washington D C, USA, 2004 |
| [18] | Mesmoudi M M, de Floriani L, Magillo P. Morphological Analysis of Terrains Based on Discrete Curvature and Distortion[C]. ACM Int. Conf. on Advances in Geographic Information Systems, Irvine, CA, USA, 2008 |
| [19] | Wang Jun, Yu Zeyun. A Morse-Theory Based Method for Segmentation of Triangulated Freeform Surfaces[C]. The 5th International Symposium on Visual Computing, Las Vegas, Nevada, 2009 |
| [20] | Mangan A, Whitaker R. Partitioning 3D Surface Meshes Using Watershed Segmentation[J]. IEEE Transaction on Visualization and Computer Graphics, 1999, 5(4): 308-321 |
| [21] | Milnor J. Morse Theory[M]. Princeton, New Jersey: Princeton Univ. Press, 1963 |
| [22] | Schneider B. Extraction of Hierarchical Surface Networks from Bilinear Surface Patches[J]. Geographical Analysis, 2005, 37:244-263 |
| [23] | Pfaltz J L. Surface Networks[J]. Geographical Analysis, 1976(8):77-93 |
| [24] | Banchoff T. Critical Points and Curvature for Embedded Polyhedral Surfaces[J]. American Mathematical Monthly, 1970, 77(5):475-485 |
| [25] | Vitali M, Floriani L D, Magillo P. Analysis and Comparison of Algorithms for Morse Decompositions on Triangulated Terrains[R]. Technical report DISI-TR-12-03, DISI, University of Genova, Genova, Italy, 2012 |
| [26] | Cǒmic L, de Floriani L, Papaleo L. Morse-Smale Decomposition for Modeling Terrain Knowledge[J]. LNCS, 2005, 3 693: 426-444 |
 2015, Vol. 40
2015, Vol. 40


